[数据结构]线性结构——队列

栈和队列是两种特殊的线性表，它们的逻辑结构和线性表相同，只是其运算规则较线性表有更多的限制，故又称它们为运算受限的线性表。栈和队列被广泛应用于各种程序设计中。
队列的基本概念
队列(Queue):也是运算受限的线性表。是一种先进先出(FirstIn First Out ,简称FIFO)的线性表。只允许在表的一端进行插入,而在另一端进行删除。
队首(front):允许进行删除的一端称为队首。
队尾(rear):允许进行插入的一端称为队尾。
例如:排队购物。操作系统中的作业排队。先进入队列的成员总是先离开队列。
队列中没有元素时称为空队列。在空队列中依次加入元素a1,a2,…,an之后,a是队首元素,an是队尾元素。显然退出队列的次序也只能是a1,a2,…,an即队列的修改是依先进先出的原则进行的。

**队列的抽象数据类型定义**

ADT Queue  
{  
    数据对象:D={ ai|ai∈ElemSet, i=1,2, ..., n,n >=0}，  
    数据关系:R= {<ai-1,ai> | ai-1,ai∈D, i=2,3,...,n}约定a1端为队首,an端为队尾。  
    基本操作:  
        Create():创建一个空队列;  
        EmptyQue():若队列为空,则返回true,否则返回flase;  
        ⋯⋯  
        InsertQue(x):向队尾插入元素x;  
        DeleteQue(x):删除队首元素x;  
}  

队列的顺序表示和实现

利用一组连续的存储单元(一维数组)依次存放从队首到队尾的各个元素,称为顺序队列。
对于队列,和顺序栈相类似,也有动态和静态之分。

//静态顺序队列,其类型定义如下:   
#define MAX_QUEUE_SIZE 100  
typedef struct queue  
{   
    ElemType Queue_array[MAX_QUEUE_SIZE] ;   
    int front ;  
    int rear ;  
}SqQueue;  

队列的顺序存储结构

设立一个队首指针front,一个队尾指针rear,分别指向队首和队尾元素。

• 初始化:front=rear=0。 入队:将新元素插入rear所指的位置,然后rear加 1。

• 出队:删去front所指的元素,然后加1并返回被删 元素。 队列为空:front=rear。

• 队满:rear=MAX_QUEUE_SIZE-1或front=rear。 在非空队列里,队首指针始终指向队头元素,而

• 队尾指针始终指向队尾元素的下一位置。

  

  循环队列
  为充分利用向量空间,克服上述“假溢出”现象的方法是:将为队列分配的向量空间看成为一个首尾相接的圆环,并称这种队列为循环队列(CircularQueue)。

在循环队列中进行出队、入队操作时,队首、队尾指针仍要加1,朝前移动。只不过当队首、队尾指针指向向量上界(MAX_QUEUE_SIZE-1)时,其加1操作的结果是指向向量的下界0。这种循环意义下的加1操作可以描述为:

if(i+1==MAX_QUEUE_SIZE)  
    i=0;  
else  
    i++;  
//其中:i代表队首指针(front)或队尾指针(rear);  
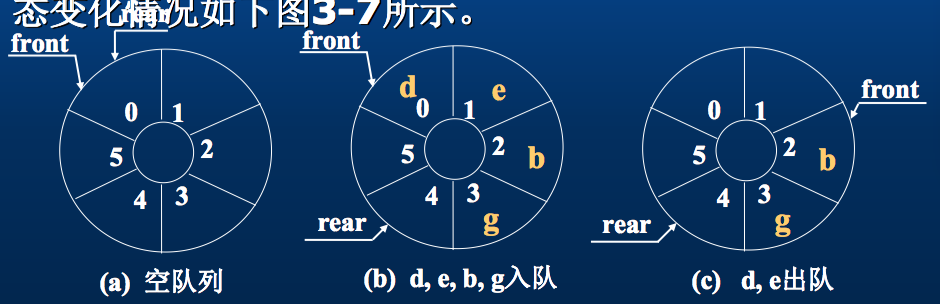
//用模运算可简化为:i=(i+1)%MAX_QUEUE_SIZE;  

显然,为循环队列所分配的空间可以被充分利用,除非向量空间真的被队列元素全部占用,否则不会上溢。因此,真正实用的顺序队列是循环队列。如，设有循环队列QU[0,5],其初始状态是front=rear=0,各种操作后队列的头、尾指针的状态变化情况如下图所示

入队时尾指针向前追赶头指针,出队时头指针向前 追赶尾指针,故队空和队满时头尾指针均相等。因此, 无法通过front=rear来判断队列“空”还是“满”。解决 此问题的方法是:约定入队前,测试尾指针在循环意义 下加1后是否等于头指针,若相等则认为队满。即:

• rear所指的单元始终为空。

• 循环队列为空:front=rear。

• 循环队列满:(rear+1)%MAX_QUEUE_SIZE =front。

//循环队列的初始化  
SqQueue Init_CirQueue(void)  
{   
    SqQueue Q;   
    Q.front=Q.rear=0;   
    return(Q);  
}  
//入队操作    
Status Insert_CirQueue(SqQueue Q , ElemType e)  
/* 将数据元素e插入到循环队列Q的队尾 */  
{   
    if ((Q.rear+1)%MAX_QUEUE_SIZE== Q.front)  
        return ERROR; /* 队满,返回错误标志 */  
    Q.Queue_array[Q.rear]=e; /* 元素e入队 */  
    Q.rear=(Q.rear+1)% MAX_QUEUE_SIZE; /* 队尾指针向前移动 */  
    return OK; /* 入队成功 */   
}  

//出队操作    
Status Delete_CirQueue(SqQueue Q, ElemType *x )  
/* 将循环队列Q的队首元素出队 */   
{   
    if (Q.front+1== Q.rear)  
        return ERROR; /* 队空,返回错误标志 */   
    *x=Q.Queue_array[Q.front]; /* 取队首元素 */   
    Q.front=(Q.front+1)% MAX_QUEUE_SIZE;/* 队首指针向前移动 */   
    return OK ;  
}  

队列的链式表示和实现

队列的链式存储结构简称为链队列,它是限制仅在表头进行删除操作和表尾进行插入操作的单链表。需要两类不同的结点:数据元素结点,队列的队首指针和队尾指针的结点。

//数据元素结点类型定义:  
typedef struct Qnode  
{   
    ElemType data;  
    struct Qnode *next;   
}QNode;  
//指针结点类型定义:  
typedef struct link_queue  
{   
    QNode *front , *rear;   
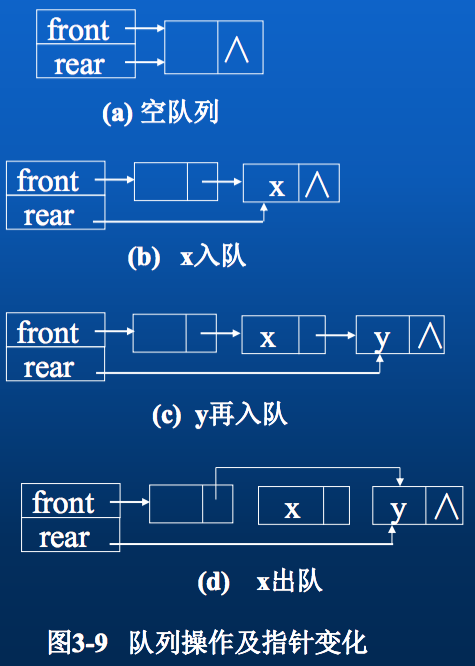
}Link_Queue;  

链队运算及指针变化
链队的操作实际上是单链表的操作,只不过是删除在表头进行,插入在表尾进行。插入、删除时分别修改不同的指针。

//链队列的基本操作  
//链队列的初始化  
LinkQueue *Init_LinkQueue(void)   
{   
    LinkQueue *Q ;   
    QNode *p ;  
    p=(QNode *)malloc(sizeof(QNode)) ; /* 开辟头结点 */   
    p->next=NULL ;  
    Q=(LinkQueue *)malloc(sizeof(LinkQueue)) ;/* 开辟链队的指针结点 */   
    Q.front=Q.rear=p ;   
    return(Q) ;  
}  

//链队列的入队操作    
//在已知队列的队尾插入一个元素e ,即修改队尾指针 (Q.rear)。  
Status Insert_CirQueue(LinkQueue *Q , ElemType e)  
/* 将数据元素e插入到链队列Q的队尾 */   
{   
    p=(QNode *)malloc(sizeof(QNode)) ;  
    if (!p)   
        return ERROR;  
    /* 申请新结点失败,返回错误标志 */  
    p->data=e ;   
    p->next=NULL ; /* 形成新结点 */   
    Q.rear->next=p ;   
    Q.rear=p ; /* 新结点插入到队尾 */   
    return OK;  
}  

//链队列的出队操作    
Status Delete_LinkQueue(LinkQueue *Q, ElemType *x)  
{  
    QNode *p ;  
    if (Q.front==Q.rear)   
        return ERROR ; /* 队空 */   
    p=Q.front->next ; /* 取队首结点 */   
    *x=p->data ;  
    Q.front->next=p->next ; /* 修改队首指针 */  
    if (p==Q.rear)   
        Q.rear=Q.front ;/* 当队列只有一个结点时应防止丢失队尾指针 */   
    free(p) ;  
    return OK ;   
}  

//链队列的撤消    
void Destroy_LinkQueue(LinkQueue *Q ) /* 将链队列Q的队首元素出队 */  
{   
    while (Q.front!=NULL)  
    {   
        Q.rear=Q.front->next;/* 令尾指针指向队列的第一个结点 */   
        free(Q.front); /* 每次释放一个结点 */  
        Q.ront=Q.rear;/* 第一次是头结点,以后是元素结点 */   
    }   
}