1.1计算机中数的表现方法

       进位计数制——指用一组固定的数字符号和特定的规则来表示数的方法，例如：二进制、八进制、十进制、十六进制等等。

       在微型计算机中采用只有0和1两个数字的二进制来表示数，这是因为计算机是一种电子设备，由大量只能识别电信号和逻辑部件组成，如：可以用电平的高低（在51单片机中，低电平（一般为0v）表示0，高电平（一般为5v）表示1，即若是将连接单片机上的某个连接二极管阴极的引脚在程序中置0，则cpu执行程序后会使该引脚输出高电平，二极管的阴极连接VCC（5v,高电平），则二极管亮。开关的通断（矩阵键盘中，按键按下代表一个状态，一个状态可以是1或0，由它们所连引脚的电平状态决定）来表示数字0和1。

       每个16进制都可以用4位二进制来表示，如：0AH = 1010B（0A是数，H和B分别表示十六进制和二进制），由于十六进制与二进制之间的转换很方便，数位长度又只有二进制的1/4，因此，在计算机中许多地方都用十六进制表示，i例如：地址。

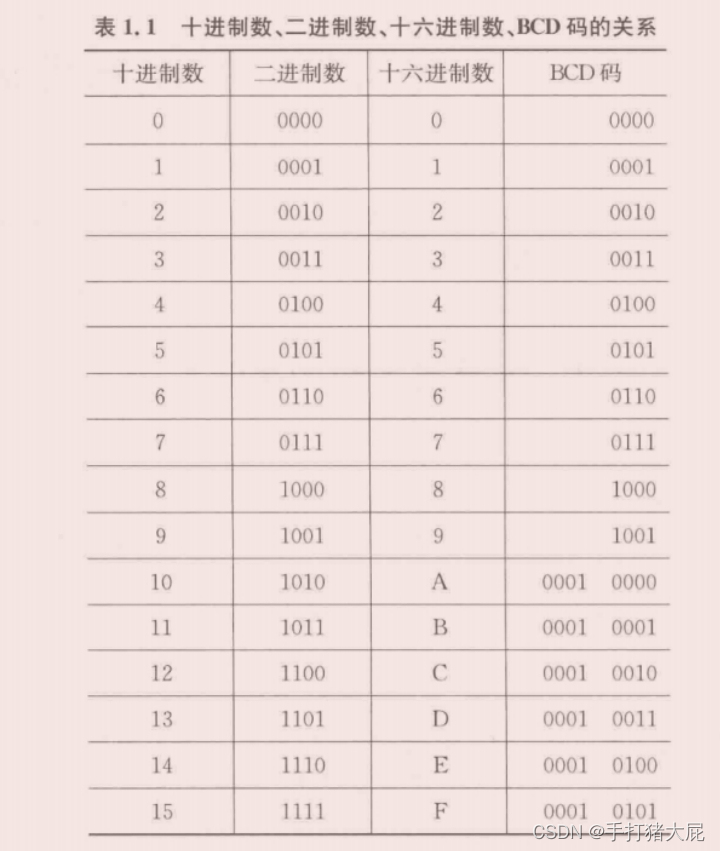
                                                                          ——图片转自《微型计算机原理与接口技术》

BCD码——有0、1、2......,9共是个不同的数字符号，也是逢十进一，但它的每一位数字都用二进制表示，例如：27（十进制） = （0010 0111）左边四位二进制是2，右边是7。

 

       十进制与二进制之间的转换

以十进制数27为例，先用十进制数27除以2，得到商13，余1（转换为二进制时的最低位），然后再用13除以2，得6余1——6再除2，得3余0——3再除2，得1余1——1再除2，得0余1。最后将最余数按照先后顺序，从二进制的最低位开始排，即结果为1 1 0 1 1 = 27。其余进制数，则可以通过先转换位十进制数，再由十进制数转换为二进制数。

 

       位、字节、字和字长等数据单位显示

位（Bit）：二进制的一个0或1就是一位，是计算机中信息存储的最小单元，计算机中的数据都是用二进制来表示，那是计算机能明白的语言。

字节（Byte）：8个二进制组成的一个单位称为一个字节，1Byte = 1Bit。

字：一个字由十六位二进制数/两个字节组成，前八位为低字节，后八位为高字节。

字长：字长决定了计算机内部一次可处理的二进制代码的位数，它取决于计算机内部的运算器、通用寄存器和数据总线的位数。例如我们目前日常所说的，64位计算机就是一次可以处理64位二进制代码。

       二进制编码——在计算机中所有的数据都采用二进制表示，但二进制对于我们来说理解起来相对效率低下。因此各种数字、符号、字母、运算符号等，都要采用若干特定的二进制组合表示，这就是二进制编码，最常用的编码有BCD码和ASCII码两种。

• BCD码——以四位二进制数为一个单位来表示十进制、十六进制等，有0、1、2......,9共是个不同的数字符号，也是逢十进一，但它的每一位数字都用二进制表示，例如：27（十进制） = （0010 0111）左边四位二进制是2，右边是7。

• ASCII码（American Standar Code for Information Interchange 美国标准信息交换码）——它用七位代码（00~7FH）来表示计算机储存的数字、字母以及符号，共可表示128个字符。

       带符号数的表示方法

通常某个数的二进制的最高位为符号位，正数为1，负数为0。连同符号位一起的一个二进制数称为机器数，它表示的真实数值称为机器数的真值，即若一个八位（D0~D7)的进制数 1001 1011

D7 = 1表示这个数是正数，剩余的位数表示27，为其真值。

       为了运算方便，机器数通常有三种表示方式：原码、反码、补码。

原码——正数的符号位用0表示，负数用1表示，其余位为数值。

因为一般的计算机中是没有减法运算部件的，因此减法运算也必须用加法表示，而反码和补码的出现正是为了方便计算机做异号运算。

反码——正数的反码与原码相同，最高位为符号位，用0表示，其余为数值；负数的反码为它的正数连同符号位一起按位取反（运算前是1，取反后就是0）。即若是

[+4]反码 = 0000 0100B；

[-4]反码 = 1111 1011B；

[-31]反码 = 1110 0000B；

即若想让一般的计算机做4 - 31的运算就要转换成4+（-31），连同符号位一起运算后为 1101 1000，这个结果当然不对，因为当带符号数用反码表示时，其最高位为符号位，当它为正数时，后7位为真正的值，当它为负数时，后7位要取反后才能得到真正的值，因此最终结果 = 1010 0111 = -27。

补码——正数的补码表示与原码相同，最高位为符号位，用0表示，其余位为真值，负数的补码最高位为1，数值部分则由它的反码再加1形成，同样其存在的意义也是方便计算机做异号运算，当一个八位二进制数的符号位为0时，表示正数，它的后7位为真正的值，当符号位为1时，要将后7位的最低位减1，求得反码，再按位取反才能得到真正的值。