尝试从数学的角度分析三国杀国战的胜率

序

2008年，桌游《三国杀》横空出世，火遍大江南北，短时间内就成为了中国最受欢迎的桌面游戏之一。2012年《三国杀国战》发售，不同于传统身份玩法，国战的阵营组合更加丰富，双将的玩法也让游戏的可玩性再次得到大大提升。新元素的加入使得国战的难度大大高于传统身份局，玩家不仅需要掌握正确的牌序，还需要时刻保持良好的大局观。
官方网络游戏《三国杀Online》是广大三国杀玩家除线下游戏以外的不二选择。由于游戏中没有国战的天梯系统，因此胜率成为了评判玩家游戏实力的一个决定性的标准。一个较为普遍的经验是，胜率超过大约36%的玩家可以说是实力较为优秀，而胜率超过39%~40%的玩家则可以说是实力出类拔萃。
一名玩家的胜率到底如何反映出他的水平？本文尝试从数学的角度对此作出分析。
（注意：最近《三国杀Online》中新加入了晋势力武将，本文不对该势力加以考虑）

单局游戏的胜率

要研究一名玩家的总胜率，我们首先关心的当然就是单局游戏的胜率。事实上，知乎上已经有答主对单局游戏的胜率进行过计算，结果是32.72%。知乎网址
注意到在该答主的计算中，假设了武将池是无限的，即一名玩家所选的将不会影响到其他玩家选将的概率。笔者认为这是不合理的，因为国战拓展包较少，在《三国杀Online》的当前版本中，只有83个武将，再加上国战双将机制，使得将池的有限性进一步加大。因此本文将将池看做有限，并再次对国战胜率期望进行计算。

---

为了计算的简便，我们假设将池中共有80名武将,并假设所有玩家水平相同，选将无任何偏好（比如无脑选魏）。由于国战的双将制对我们计算胜率期望没有影响，因此我们不妨假设将池中共有40名武将，其中魏蜀吴群各10个，每局游戏每名玩家只选一名武将。
由以上假设我们可以知道，一名玩家进行了本局游戏最后一次击杀的概率是$\frac{1}{8}$，因此一个势力有n名玩家， 那么该势力在本局游戏中的胜率就是$\frac{n}{8}$。
一局游戏中，设$P_i(i=0,1,...,7)$是与自己同势力的玩家（不包括自己）有$i$个的概率，这里我们先不考虑野心家机制。由于每个玩家选择武将是独立的，因此我们可以得到公式$P_i=\frac{C_9^i{C}_{30}^{7-i}}{C_{39}^7}$。
当$i\le 3$时，自己获胜的概率就是$\frac{i+1}{8}{P}_i$；
而当$i\ge 4$时，由于野心家机制，自己有$\frac{i-3}{i+1}$的概率成为野心家，因此自己获胜的概率就是$(\frac{1}{8}\frac{i-3}{i+1}+\frac{4}{8}\frac{4}{i+1})P_i$。
由此，我们可以得到胜率$$=\sum _{i=0}^3\frac{i+1}{8}{P}_i+\sum _{i=4}^7(\frac{1}{8}\frac{i-3}{i+1}+\frac{4}{8}\frac{4}{i+1})P_i=31.88\%$$
这个结果比知乎答主计算的结果低了将近一个百分点，这是合理的，因为将池有限限制了单阵营多将的概率，而单阵营多将的胜率更高，所以考虑将池有限之后，胜率是会降低的。

胜率的分布

在研究了单局游戏的胜率之后，我们自然希望研究一名玩家的总胜率是如何分布的，由此我们就能知道某个胜率的玩家的水平究竟如何。不考虑玩家心态等因素的情况下，一名玩家的两局游戏之间是没有任何关联的，那么一名玩家进行了n局游戏后，他的总胜率服从二项分布$B(n,P)$。当n=1000时，总胜率的概率密度曲线如下：
二项分布的性质保证了峰值所对应的胜率为0.319，这也是总胜率的数学期望。下图给出了总胜率的分布函数：

由图可以看出，假设所有玩家的总胜率都服从这个分布，那么玩家胜率在36.5%以上的概率只有0.1%，这显然和文章开头所说的普遍经验是相悖的。问题出在了哪里？我们进入下一节。

实际数据

为了研究实际游戏中玩家总胜率的分布，笔者在游戏中随机抽取了400名玩家的胜率（随机观战），绘成了一副柱状图：

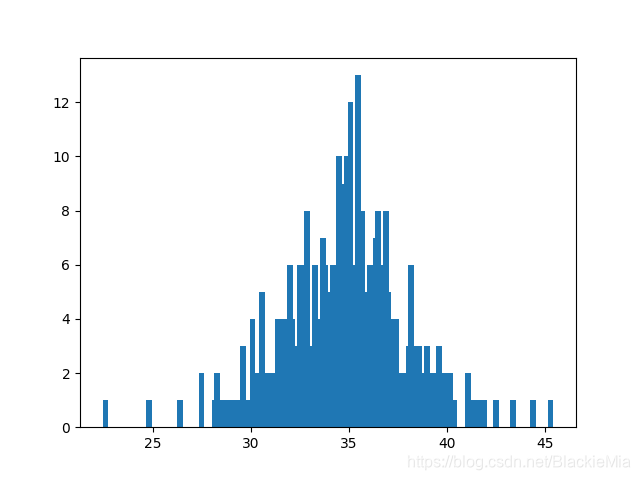
样本近似服从正态分布（中心极限定理保证了这是合理的）。然而，样本的均值高达34.8%，这与我们计算出来的31.9%有很大的差距。笔者认为，这是由于玩家之中普遍存在选将偏好导致的。例如，在鏖战版本以前，魏国武将强度很高，玩家倾向于选魏国；而鏖战版本后，玩家对吴国的喜好也日渐上升。这一偏好可以通过调整选择各个势力的概率来量化，相关计算较为复杂，这里不深入讨论。但是从定性的角度来说，当玩家普遍存在选将偏好时，单阵营多将的概率将提高，而此时胜率最高，因此选将偏好会导致总体胜率偏高。
令$P=34.8\%$后，我们再次研究二项分布$B(n,P)$，分布函数如下：
由图可知，胜率在36.7%以上的玩家只有大约10%，而在39.5%以上的玩家只有0.1%。但事实上，在上述样本所产生的分布函数中，对应90%概率的胜率为38.6%，而且39.5%胜率只对应94%的概率，这与笔者所构造的模型仍有一些出入。实际情况下，玩家胜率满足的正态分布的标准差要比模型中的要大，笔者分析可能是因为低胜率玩家退游率较高，导致玩家胜率分布倾向于偏态分布，从而导致高胜率人数比理想状态下要更多。

（如果你有更好的想法，欢迎与我交流）