秋招突击——算法打卡——5/31——复习{采药问题、（状态压缩DP）小国王}——新做：{盛最多水的容器、整数转罗马数字}

复习

背包模型——采药问题

• 原题链接
• 这里回忆的时候，还是有点问题，就是起点值怎么写？并不确定！
• 然后关于这个表达式，也是弄了半天才想起来，还是要多多练习一下！

#include <iostream>
#include <algorithm>

using namespace std;
const int T = 1010;
const int M = 110;
int t[M],w[M];
int f[M][T];
int f1[T];
int n,m;

int main(){
   
    cin>>n>>m;
    for (int i = 1; i <= m; ++i) {
   
        cin>>t[i]>>w[i];
    }

    // 遍历所有的药物
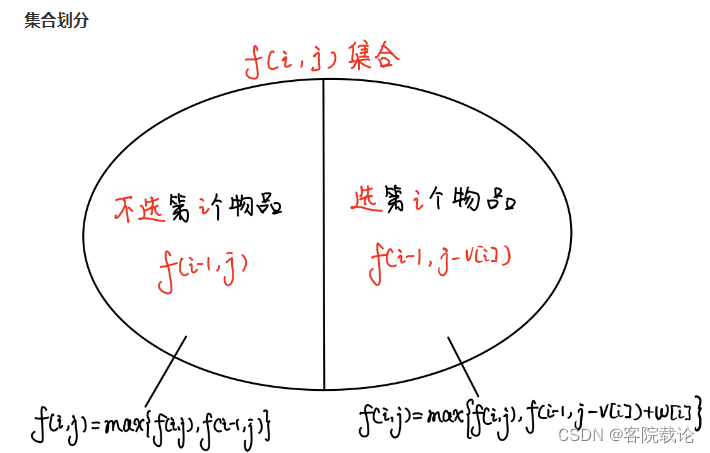
    // f[i][j]:表示在前i个物体下，容量为j的若干种装法中，最高的价值
    // 集合划分，对于第i个物体而言，也就是两种情况，装或者不装，装f[i-1][j - t[i]] + w[i],不装f[i-1][j]
    int res = 0;
    for (int i = 1; i <= m; ++i) {
   
        // 什么时候置零是一个问题，不知道怎么办
        f[i][0] = 0;
        for (int j = 1; j <= n && t[i] <= j; ++j) {
   
            f[i][j] = max(f[i-1][j],f[i -1][j - t[i]] + w[i]);
            res = max(res ,f[i][j]);
        }
    }
    cout<<res;

    // 使用滚动矩阵进行优化
    for (int i = 1; i <= m ; ++i) {
   
        for (int j = n; j >=  1 && t[i] <= j; j--) {
   
            f1[j] = max(f1[j],f1[j - t[i]] + w[i]);
        }
    }
    cout<<f[n]<< endl;
}

• 关于二维数组，基本思路是对的，就分两种情况，装或者不装，但是你得分开写
  参考信息
  

状态压缩DP——小国王

• 题目内容
  

思路分析

• 参考链接：状态压缩
• 这道题是真的不会，当时听了半天都没听懂，然后直接跳过了，但是也是dp的一种，经常考，还是要学习一下啊。
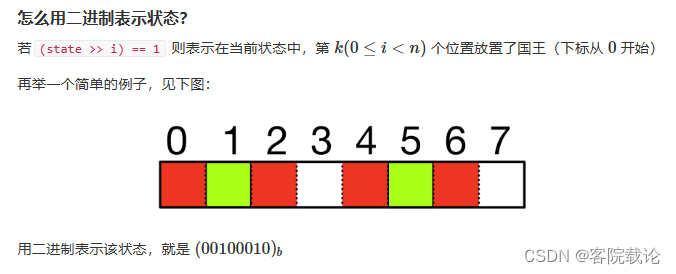
• 这里是使用二进制表示某一个行数的棋盘的状态

• 今天是不可能完全搞懂了，就搞懂局部吧，半个小时能懂多少懂多少，不然没时间搞别的东西了。再看一遍，也觉得是昏了头了，即使要是考了这个，直接跳过吧。

• 第i行的摆放位置，仅仅和第i-1行是有关系的，所以仅仅需要考虑第i-1的状态

• 第i行可以摆放x中状态，然后在判断一下是否和第i-1行是合法的，然后在进行累加，所以需要干两件事

  • 检查第i行的状态和第i-1行状态是否是合法的
  • 第i行有哪些合法状态
    暂时就分析到这里，明天就是看看代码还有怎么计算预设的状态转换了。
    

实现代码参考

#include <iostream>
#include <vector>

using namespace std;

typedef long long LL;

const int N = 11, M = 1 << N