排列 组合 辨析

省流总结：

排列：

没有for循环，直接确定选与不选 在dfs（）条件中进行加减计算

组合 

有for循环，且for循环的  i 有两种情况：

1. 从1到n遍历，每次递归调用都可能选择数组中的任何未访问过的元素

2. 从当前索引x开始遍历到n，递归调用只会考虑当前索引之后未访问过的元素

一、排列问题

选与不选

题目：P2036 [COCI2008-2009 #2] PERKET - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include<bits/stdc++.h>
using namespace std;

struct{
	int s,b;
}p[15]; 
int n;
int vis[15] ={0};
int res = 1e+9;


void dfs(int x,int sourSum,int betterSum){

	 if(x == n+1){
	 	if(sourSum == 1 && betterSum == 0) return;
	 	res = min(abs(betterSum - sourSum),res);
	 	return ;
	 }

      dfs(x + 1 ,sourSum * p[x].s , betterSum + p[x].b);
      dfs(x + 1 ,sourSum,betterSum);
	
}

int main(){
	cin>>n;
	for(int i = 1 ; i <= n ; i++){
		cin>>p[i].s>>p[i].b;
	}
	
	dfs(1,1,0);
	cout<<res<<endl;
}

和背包问题一样 。不能改成for循环，否则就是组合问题，

二、组合数问题

例题1

解空间大小为2^n，选与不选，但区别在于for循环针对于其下标

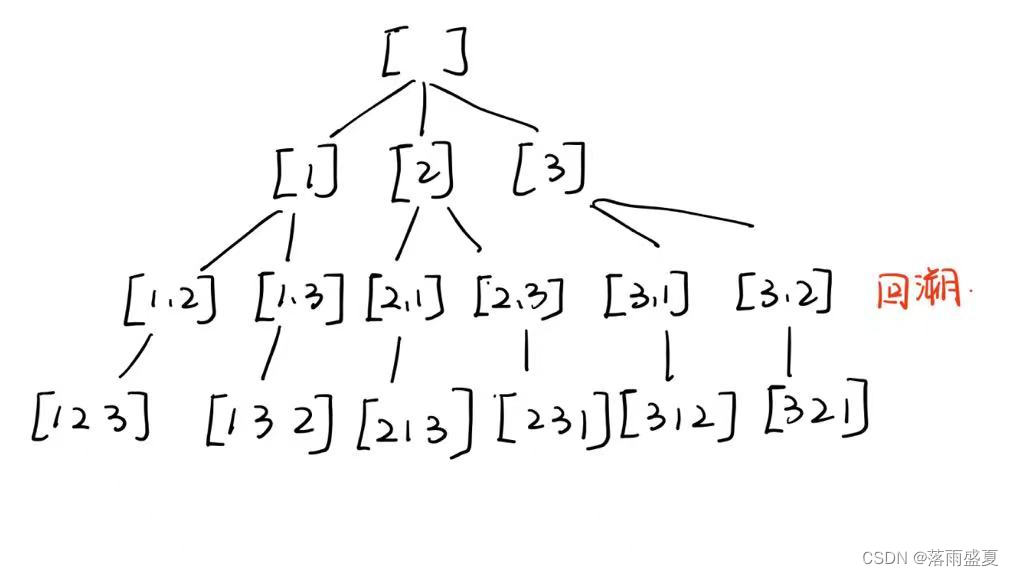
for循环从1开始

void dfs(int x){
	if(x == n+1){//所有数全部排列完成 
		//output
		return;
	} 
	for(int i = 1 ;i <= n; i++){
		if(vis[i] == 0){//没有遍历过 
			vis[i] = 1;
			a[x] = i;//存储该数
			dfs(x+1); //位置加1  
			vis[i] = 0;//回溯 
		}
	}
	//可以使用vector存储
	/*for(int i = 1 ; i <= n ;i++){
		if(!vis[i]){
			vis[i] = 1;
			p.push_back(i);
			dfs(x+1);
			vis[i] = 0 ;
			p.pop_back();//一定要弹出哦 
		}
	} 
	*/
}

dfs(x+1)；//注意这个地方只是位置增加，但是for循环里面i还是从1开始，还是一个一个看有没有访问过，没访问的往里面加元素，和排列很像但思想不一样，注意区别。

例题2

问题规模n!，两两组合

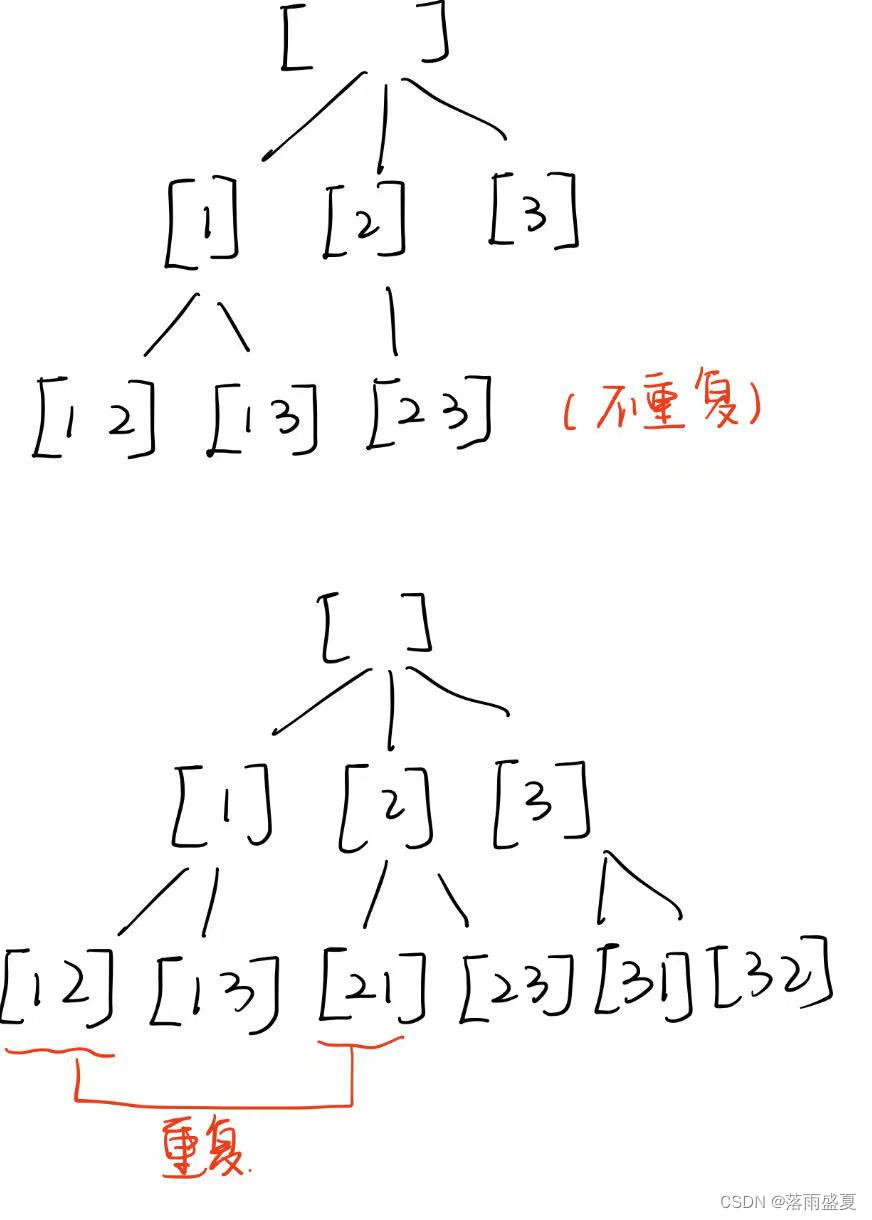
void dfs(int start,int res){
	if(组成数的个数达到要求){// 
		//output
		return;
	} 

	for(int i = start ; i <= n ;i++){
		if(!vis[i]){
			vis[i] = 1;
			p.push_back(i);
			dfs(start+1,res+1);
		}
	} 
	
}

此时for 循环从i = start 开始，且start +1 ，保证不重复 

例一和例二 区别 

例题1和例题2代码总结区别：

1.
void dfs(int x,int sourSum,int betterSum){

	 if(x == n+1){
	 	if(sourSum == 1 && betterSum == 0) return;
	 	res = min(abs(betterSum - sourSum),res);
	 	return ;
	 }

      for(int i = 1 ; i <= n ; i++){
      	if(vis[i] == 0){
      		vis[i] = 1;
      		dfs(x+1,sourSum * p[i].s , betterSum + p[i].b );
      		vis[i] = 0;
		  }
	  }
	
}

2.
void dfs(int x,int sourSum,int betterSum){

	 if(x == n+1){
	 	if(sourSum == 1 && betterSum == 0) return;
	 	res = min(abs(betterSum - sourSum),res);
	 	return ;
	 }
	 for(int i = x ; i <= n ; i++){
      	if(vis[i] == 0){
      		vis[i] = 1;
      		dfs(x+1,sourSum * p[i].s , betterSum + p[i].b );
      		vis[i] = 0;
		  }
	  }
	
}

相同点：都是for循环，退出条件一致

不同点：

代码1 中从1开始遍历到n，每次递归调用都可能选择数组中的任何未访问过的元素

代码2中从当前索引x开始遍历到n，递归调用只会考虑当前索引之后未访问过的元素

例题3

选数问题

给定若干个正整数a0、a0 、…、an-1 ，从中选出若干数，使它们的和恰好为k，

要求找选择元素个数最少的解。如果有多个最优解，输出字典序最小的。

输入格式:

输入有两行，第一行给出2个正整数n,k，用空格分隔。第二行是用空格分隔的n个整数。

输出格式:

输出有两行，第一行从小到大输出选择的元素，第二行输出元素的个数。

输入样例:

在这里给出一组输入。例如：

5 9
1 1 4 5 7

输出样例:

在这里给出相应的输出。例如：

4 5
2

注意该问题的限制条件

子集和 字典序列最小（包含的数个数最少的）

//组合数从第二个开始选择
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int a[10000];
int n,k;
int vis[1000];
vector<int> p;
vector<int> c;
int minn = 100;//定义最少元素个数
void dfs(int start,int sum,int size){
    if(sum == k){
        if(minn>size){
            minn = size;//记录最小元素元素个数
            c.clear();
            for(int i = 0 ;i<size;i++)
                c.push_back(p[i]);
        }
    }
    if(start >= n) return ;
    if(sum > k) return ;
    for(int i = start ;i < n;i++){
        if(!vis[a[i]]){
            vis[a[i]] = 1;
            p.push_back(a[i]);
            dfs(start+1,sum+a[i],size+1);//组合问题
            vis[a[i]] = 0;
            p.pop_back();
        }
    }
}
int main(){
    cin>>n>>k;
    for(int i = 0 ;i < n;i++)
        cin>>a[i];
    sort(a,a+n);
    dfs(0,0,0);
    for(int i = 0; i < c.size();i++){
        cout<<c[i];
        if(i!=c.size()-1){
            cout<<" ";
        }
        else cout<<endl;
    }
    cout<<c.size();
    return 0;
}