最短路径问题

一、原题

最短路径问题(floyed.cpp dijkstra.cpp)

题目描述

平面上有n个点(n<=100)，每个点的坐标均在-10000～10000之间。其中的一些点之间有连线。若有连线，则表示可从一个点到达另一个点，即两点间有通路，通路的距离为两点间的直线距离。现在的任务是找出从一点到另一点之间的最短路径。

输入

第1行：1个整数n
第2..n+1行：每行2个整数x和y，描述了一个点的坐标
第n+2行：1个整数m，表示图中连线的数量
接下来有m行，每行2个整数i和j，表示第i个点和第j个点之间有连线
最后1行：2个整数s和t，分别表示源点和目标点

输出

第1行：1个浮点数，表示从s到t的最短路径长度，保留2位小数

样例输入

5
0 0
2 0
2 2
0 2
3 1
5
1 2
1 3
1 4
2 5
3 5
1 5

样例输出

3.41

二、分析

根据以上的样例数据，我总结出了下列直角坐标系的草图。

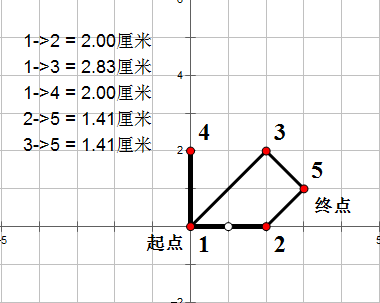
我们明显开出起点1到终点5的最短路径为$\overline {125}$。2.00+1.41=3.41，刚好符合样例数据。
在此时解释一下：dis[u][v]代表从u到v最短距离的长度，w[u][v]代表连接u、v的边的长度。
然后我们首先要初始化，把各个点之间的距离用一个double数组存起来。以下是初始化步骤。
初始化要运用勾股定理和直角坐标系的知识。所以A点到B点的距离等于以下式子。

$$AB=\sqrt{(X_A-Y_A)^2+(X_B-Y_B)^2}$$

#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;
struct point{
    int x,y;
}point[105];//存储点的x.y轴
int n,m;
double dis[105][105];
bool a[105][105];
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>point[i].x>>point[i].y;
    cin>>m;
    for(int i=1;i<=m;i++){//存储邻接表
        int x,y;
        cin>>x>>y;
        a[x][y]=a[y][x]=1;
    }
    memset(dis,127,sizeof(dis));//设为极大值
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(a[i][j]){//如果两点连通
                int x=point[i].x-point[j].x,y=point[i].y-point[j].y;
                dis[i][j]=sqrt(pow(x,2.0)+pow(y,2.0));//利用勾股定理求两点之间的距离
            }
}

初始化完，我们就来分类讨论floyed算法和dijkstra算法。

Floyed算法

Floyed算法，是最简单的最短路径算法，可以计算图中任意两点间的最短路径。Floyed的时间复杂度是$O(N^3)$，可以处理负边权的情况。

算法描述

1. 初始化（刚才已经初始化了）
2. 执行以下循环
3. 输出dis[i][j]即可

for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(dis[i][j]>dis[i][k]+dis[k][j])
                    dis[i][j]=dis[i][k]+dis[k][j];

算法分析

三层循环，第一层循环中间点k，第二、三层循环起点终点i、j，算法的思想很容易理解：如果点i到点k的距离加上点j的距离小于原先点i到点j的距离，就用这个更短的距离来更新原先点i到点j的距离。

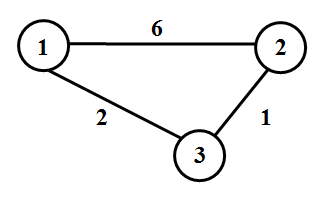
在上图中，因为dis[1][3]+dis[3][2]<dis[1][2]，所以就用dis[1][3]+dis[3][2]更新1到2的距离。

算法变形

如果是一个没有边权的图，把相连的两点间的距离设为dis[i][j]=true，不相邻的两边dis[i][j]=false，就可以变形（伪代码）：

    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                dis[i][j]=dis[i][j]||(dis[i][k]&&dis[k][j]);

Dijkstra算法

用来计算从一个点到其他所有点的最短路径的算法，是一种单源最短路径算法。
Dijkstra的时间复杂度是$O(N^2)$，不可以处理存在负边权的情况。

算法介绍

1. 设起点为s，dis[v]表示从s到v的最短路径，pre[v]为v的前驱结点，用来输出路径。
2. 初始化：dis[v]=$\infty$（v≠s）；dis[s]=0；pre[s]=0；
3. for(int i=1;i<=n;i++)
   ①在没有被访问过的点找一个顶点u，使得dis[u]是最小的。
   ②u标记为已确定的最短路径。
   ③for与u相连的每个未确定最短路径的顶点v。（见下方代码）
4. dis[v]为s到v的最短距离；pre[v]为v的前驱结点，用来输出路径。

    if(dis[u]+w[u][v]<dis[v]){
        dis[v]=dis[u]+w[u][v];
        pre[v]=u;
    }

三、源代码

Floyed算法

#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;
struct point{
    int x,y;
}point[105];//存储点的x.y轴
int n,m;
double dis[105][105];
bool a[105][105];
int main()
{
    //freopen("floyed.in","r",stdin);
    //freopen("floyed.out","w",stdout);
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>point[i].x>>point[i].y;
    cin>>m;
    for(int i=1;i<=m;i++){//存储邻接表
        int x,y;
        cin>>x>>y;
        a[x][y]=a[y][x]=1;
    }
    memset(dis,127,sizeof(dis));//设为极大值
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(a[i][j]){//如果两点连通
                int x=point[i].x-point[j].x,y=point[i].y-point[j].y;
                dis[i][j]=sqrt(pow(x,2.0)+pow(y,2.0));//利用勾股定理求两点之间的距离
            }
    for(int k=1;k<=n;k++)//Floyed算法
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(dis[i][j]>dis[i][k]+dis[k][j])
                    dis[i][j]=dis[i][k]+dis[k][j];
    int x,y;
    cin>>x>>y;
    printf("%.2lf",dis[x][y]);//输出x（起点）到y（终点）的最短路径
}

Dijkstra算法

#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
using namespace std;
const int MAXN=100;
struct point{
    int x,y;
}point[MAXN+5];//存储点的x.y轴
double c[MAXN+5],f[MAXN+5][MAXN+5],min1;
bool b[MAXN+5];
int n,m,s,e;
int main()
{
    //freopen("dijkstra.in","r",stdin);
    //freopen("dijkstra.out","w",stdout);
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>point[i].x>>point[i].y;
    memset(f,127,sizeof(f));
    cin>>m;
    for(int i=1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        f[x][y]=f[y][x]=sqrt(pow(point[x].x-point[y].x,2.0)+pow(point[x].y-point[y].y,2.0));//直接运用勾股定理运算
    }
    cin>>s>>e;//读入开始与结束点
    for(int i=1;i<=n;i++)
        c[i]=f[s][i];
    memset(b,false,sizeof(b));//bool数组重置
    b[s]=true;//起点为true
    c[s]=0;//起点到起点距离为0
    for(int i=1;i<n;i++){
        min1=1e30;//设min1为极大值
        int k=0;
        for(int j=1;j<=n;j++)
            if(!b[j]&&c[j]<min1){
                min1=c[j];
                k=j;
            }
        if(k==0)//k没有被改变，跳出循环
            break;
        b[k]=true;
        for(int j=1;j<=n;j++)//算法核心
            if(c[k]+f[k][j]<c[j])
                c[j]=c[k]+f[k][j];
    }
    printf("%.2lf",c[e]);//输出起点到e（终点）的最短路径
}