题目描述:
计算化学式为
C
n
H
2
n
+
2
C_nH_{2n+2}
CnH2n+2的烷烃的同分异构体个数。
等价于求
n
n
n 个点的无标号无根树并且满足每个点的度数
≤
4
\le4
≤4 的树的个数。
多组数据,对998244353取模。
题解:
1. T = 1 , n ≤ 2000 1.~~~T=1,~n\le2000 1. T=1, n≤2000 :
先考虑计算有根树的数量。
设
f
(
i
,
j
)
f(i,j)
f(i,j)表示共有
i
i
i个点,且根的度数为
j
j
j的方案数。
因为相同大小的子树会涉及同构,所以按照最大子树的大小来转移,枚举
s
i
z
e
size
size从1到
n
n
n,表示当前最大子树的大小,记
s
=
∑
k
=
0
3
f
(
s
i
z
e
,
k
)
s=\sum_{k=0}^3f(size,k)
s=∑k=03f(size,k)。
转移时再枚举一个大小为size的子树的个数
k
k
k,便有转移:
f
(
i
,
j
)
+
=
f
(
i
−
s
i
z
e
∗
k
,
j
−
k
)
∗
(
s
+
k
−
1
k
)
f(i,j)~+=f(i-size*k,j-k)*\binom {s+k-1}{k}
f(i,j) +=f(i−size∗k,j−k)∗(ks+k−1)
这是
O
(
n
2
)
O(n^2)
O(n2)的,带一个
4
2
4^2
42的常数。

2. T = 1 , n ≤ 1 0 5 2.~~~T=1,~n\le10^5 2. T=1, n≤105 :
先算烷基, 即有根树并且根的度数
≤
3
≤ 3
≤3
LOJ #6538. 烷基计数 加强版 加强版
设
A
(
x
)
A(x)
A(x)为烷基大小对应个数的生成函数。
直接乘起来显然会重,但是我们有强大的Burnside引理(Polya定理):
等价类个数=每个置换的不动点数/总置换数。总置换数就是全排列个数。
单位置换的不动点数为
A
(
x
)
3
A(x)^3
A(x)3,3个交换两个位置的置换的不动点数为
A
(
x
)
A
(
x
2
)
A(x)A(x^2)
A(x)A(x2),2个交换三个位置的置换的不动点数为
A
(
x
3
)
A(x^3)
A(x3)。
所以:
A
(
x
)
=
1
+
x
A
(
x
)
3
+
3
A
(
x
)
A
(
x
2
)
+
2
A
(
x
3
)
6
A(x)=1+x{A(x)^3+3A(x)A(x^2)+2A(x^3)\over6}
A(x)=1+x6A(x)3+3A(x)A(x2)+2A(x3)
网上大多的解法是牛顿迭代,比如这篇。
我说一说分治NTT怎么做,虽然复杂度是
n
l
o
g
2
n
nlog^2n
nlog2n的,但是技巧很牛逼。
s
o
l
v
e
(
l
,
r
)
,
m
i
d
=
(
l
+
r
)
>
>
1
solve(l,r),mid=(l+r)>>1
solve(l,r),mid=(l+r)>>1
问题主要在于
[
l
,
m
i
d
]
[l,mid]
[l,mid]对
[
m
i
d
+
1
,
r
]
[mid+1,r]
[mid+1,r]作贡献时卷积会涉及到
[
m
i
d
+
1
,
r
]
[mid+1,r]
[mid+1,r]的值。
把贡献写成每一项的形式:
f
n
=
∑
i
+
j
+
k
+
1
=
n
f
i
f
j
f
k
+
∑
i
+
2
j
+
1
=
n
f
i
f
j
+
∑
3
i
+
1
=
n
f
i
f_n=\sum_{i+j+k+1=n}f_if_jf_k+\sum_{i+2j+1=n}f_if_j+\sum_{3i+1=n}f_i
fn=∑i+j+k+1=nfifjfk+∑i+2j+1=nfifj+∑3i+1=nfi
在此时我们只计算
i
,
j
,
k
∈
[
0
,
m
i
d
]
,
且
i,j,k\in[0,mid],且
i,j,k∈[0,mid],且
max
(
i
,
j
,
k
)
∈
[
l
,
m
i
d
]
\max(i,j,k)\in[l,mid]
max(i,j,k)∈[l,mid]的情况,就避免涉及到
[
m
i
d
+
1
,
r
]
[mid+1,r]
[mid+1,r]的
f
f
f。
对于上式的最后一项,每一个 n n n最多只会有一个 i i i产生贡献,递归到 l = = r l==r l==r时计算一下即可。
对于
∑
i
+
j
+
k
+
1
=
n
f
i
f
j
f
k
\sum_{i+j+k+1=n}f_if_jf_k
∑i+j+k+1=nfifjfk:
首先有一个常识:对于
s
o
l
v
e
(
0
,
n
)
solve(0,n)
solve(0,n)中的
s
o
l
v
e
(
l
,
r
)
solve(l,r)
solve(l,r),当
l
≠
0
l\neq0
l=0 时,
2
∗
l
>
r
2*l >r
2∗l>r,列几项就可以发现。
若
l
≠
0
l\neq 0
l=0 ,
i
,
j
,
k
i,j,k
i,j,k 中至多只能有一项
≥
l
\ge l
≥l,不妨设为
i
i
i,那么
j
,
k
j,k
j,k的范围就是
[
0
,
r
−
l
)
[0,r-l)
[0,r−l),用
A
[
l
,
m
i
d
]
∗
A
[
0
,
r
−
l
)
2
A[l,mid]*A[0,r-l)^2
A[l,mid]∗A[0,r−l)2,再乘上3的系数贡献到
[
m
i
d
+
1
,
r
]
[mid+1,r]
[mid+1,r]即可。需要将
A
[
l
,
m
i
d
]
A[l,mid]
A[l,mid]移位至
B
[
0
,
m
i
d
−
l
]
B[0,mid-l]
B[0,mid−l]来保证复杂度。
若
l
=
0
l=0
l=0 ,直接用
A
[
0
,
m
i
d
]
3
A[0,mid]^3
A[0,mid]3贡献到
[
m
i
d
+
1
,
r
]
[mid+1,r]
[mid+1,r]即可。
对于
∑
i
+
2
j
+
1
=
n
f
i
f
j
\sum_{i+2j+1=n}f_if_j
∑i+2j+1=nfifj:
若
l
≠
0
l\neq0
l=0,显然只能
i
∈
[
l
,
m
i
d
]
i\in[l,mid]
i∈[l,mid],
j
∈
[
0
,
(
r
−
l
)
/
2
]
j\in[0,(r-l)/2]
j∈[0,(r−l)/2],需要将
A
[
l
,
m
i
d
]
A[l,mid]
A[l,mid]移位至
B
[
0
,
m
i
d
−
l
]
B[0,mid-l]
B[0,mid−l],将
A
[
0
,
(
r
−
l
)
/
2
]
A[0,(r-l)/2]
A[0,(r−l)/2]的第
k
k
k项填到
C
[
k
∗
2
]
C[k*2]
C[k∗2],然后再用
B
[
0
,
m
i
d
−
l
]
B[0,mid-l]
B[0,mid−l]乘上
C
[
0
,
r
−
l
)
C[0,r-l)
C[0,r−l)。
若
l
=
0
l=0
l=0,直接用
A
[
0
,
m
i
d
]
A[0,mid]
A[0,mid]乘上
C
[
0
,
r
−
l
)
C[0,r-l)
C[0,r−l)即可,代码可以和
l
≠
0
l\neq0
l=0 的情况统一起来。
这里是我的代码,删掉注释之后其实很短。
算出烷基个数之后,同样利用重心和Polya定理可以计算出烷烃的个数,不再赘述。
3. T = 1 0 5 , n ≤ 1 0 5 3.~~~T=10^5,~n\le10^5 3. T=105, n≤105 :

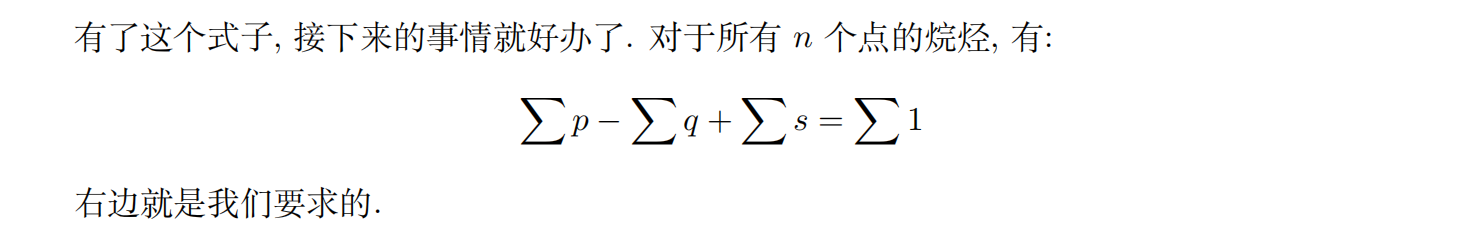
令
P
(
x
)
P(x)
P(x)表示烷烃的
∑
p
\sum p
∑p 的生成函数。对于一个无根树,选
n
n
n个点中任意一个点作根形成的互不同构的有根树的数量就是
p
p
p。对于不同构的无根树,显然不可能形成同构的有根树,所以
∑
p
\sum p
∑p 就是所有互不同构的有根树的数量。
用一下Polya定理,有:
P
(
x
)
=
x
A
(
x
)
4
+
3
A
(
x
2
)
2
+
6
A
(
x
)
2
A
(
x
2
)
+
8
A
(
x
)
A
(
x
3
)
+
6
A
(
x
4
)
24
P(x)=x{A(x)^4+3A(x^2)^2+6A(x)^2A(x^2)+8A(x)A(x^3)+6A(x^4)\over24}
P(x)=x24A(x)4+3A(x2)2+6A(x)2A(x2)+8A(x)A(x3)+6A(x4)
再令
Q
(
x
)
Q(x)
Q(x)表示烷烃的
∑
q
\sum q
∑q 的生成函数。对于一个无根树,选
n
−
1
n-1
n−1 条边中的任意一条边劈开,在中间插入一个点作根形成的互不同构的有根树的数量就是
q
q
q。即一个点两边挂两棵子树形成的所有互不同构的有根树的数量就是
∑
q
\sum q
∑q。
类似的,有:
Q
(
x
)
=
(
A
(
x
)
−
1
)
2
+
(
A
(
x
2
)
−
1
)
2
Q(x)={(A(x)-1)^2+(A(x^2)-1)\over2}
Q(x)=2(A(x)−1)2+(A(x2)−1)
然后显然
∑
s
\sum s
∑s 的生成函数就是
A
(
x
2
)
A(x^2)
A(x2)
所以最终烷烃数量的生成函数为
B
(
x
)
=
P
(
x
)
−
Q
(
x
)
+
A
(
x
2
)
B(x)=P(x)-Q(x)+A(x^2)
B(x)=P(x)−Q(x)+A(x2)
时间复杂度为 O ( n l o g n / l o g 2 n + T ) O(nlogn/log^2n+T) O(nlogn/log2n+T)。
Code:
#include<bits/stdc++.h>
#define maxn 550005
using namespace std;
inline void read(int &a){
char c;while(!isdigit(c=getchar()));
for(a=c-'0';isdigit(c=getchar());a=a*10+c-'0');
}
inline void write(int x){
if(x>=10) write(x/10);
putchar(x%10+48);
}
const int mod = 998244353, I2=(mod+1)/2,I3=(mod+1)/3,I6=(mod+1)/6,I24=1ll*I2*I2%mod*I6%mod;
typedef vector<int> Poly;
int w[maxn]={1},r[maxn],In;
inline int Pow(int a,int b){
int s=1; for(;b;b>>=1,a=1ll*a*a%mod) if(b&1) s=1ll*s*a%mod;
return s;
}
int init(int n){
int len=1;while(len<n) len<<=1;
for(int i=0;i<len;i++) r[i]=r[i>>1]>>1|(i&1?len>>1:0);
In=Pow(len,mod-2);
return len;
}
void NTT(Poly &a,int len,int flg){
if(flg==1) a.resize(len);
for(int i=0;i<len;i++) if(i<r[i]) swap(a[i],a[r[i]]);
for(int i=2,l=1,G=flg==1?3:I3;i<=len;l=i,i<<=1){
for(int k=l-2,wn=Pow(G,(mod-1)/i);k>=0;k-=2) w[k+1]=1ll*(w[k]=w[k>>1])*wn%mod;
for(int j=0;j<len;j+=i)
for(int k=j;k<j+l;k++){
int u=a[k],v=1ll*w[k-j]*a[k+l]%mod;
a[k]=(u+v>=mod?u+v-mod:u+v),a[k+l]=(u-v<0?u-v+mod:u-v);
}
}
if(flg==-1) for(int i=0;i<len;i++) a[i]=1ll*a[i]*In%mod;
}
Poly A(maxn),B(maxn),P(maxn),Q(maxn);
Poly tmp,L,C1,C2,A1(maxn),A2(maxn),A3(maxn),A4(maxn);
void solve(int l,int r){
if(l==r) {if(l%3==1) A[l]=(A[l]+1ll*A[l/3]*I3)%mod;return;}
int mid=(l+r)>>1;
solve(l,mid);
L=Poly(A.begin()+l,A.begin()+mid+1);
C1=Poly(A.begin(),A.begin()+(r-l));
C2=Poly(r-l); for(int i=0;i*2<r-l;i++) C2[i<<1]=A[i];
int len=init((r-l+1)<<1); //xun huan juan ji. (mid-l)
NTT(L,len,1),NTT(C1,len,1),NTT(C2,len,1),tmp.resize(len);
for(int i=0;i<len;i++) tmp[i]=(1ll*L[i]*C1[i]%mod*C1[i]%mod*(l?I2:I6) + 1ll*L[i]*C2[i]%mod*I2)%mod;
NTT(tmp,len,-1);
for(int i=mid+1;i<=r;i++) A[i]=(A[i]+tmp[i-l-1])%mod;
solve(mid+1,r);
}
void Pre(int n){
A[0]=1,solve(0,n-1);
for(int i=0;i<n;i++) A1[i]=A2[i*2]=A3[i*3]=A4[i*4]=A[i];
int len=init((n-1)*4+1);
NTT(A1,len,1),NTT(A2,len,1),NTT(A3,len,1),NTT(A4,len,1);
for(int i=0;i<len;i++)
P[i]=(1ll*A1[i]*A1[i]%mod*A1[i]%mod*A1[i]%mod + 6ll*A1[i]*A1[i]%mod*A2[i]%mod + 8ll*A1[i]*A3[i]%mod
+ 3ll*A2[i]*A2[i]%mod + 6ll*A4[i]%mod)*I24%mod;
NTT(P,len,-1);
for(int i=n;i>=1;i--) P[i]=P[i-1]; P[0]=0;
for(int i=0;i<len;i++) Q[i]=(1ll*(A1[i]-1+mod)*(A1[i]-1+mod)+A2[i]-1)%mod*I2%mod;
NTT(Q,len,-1);
for(int i=0;i<=n;i++) B[i]=(1ll*P[i]-Q[i]+mod+(!(i&1)?A[i>>1]:0))%mod;
}
int main()
{
freopen("alkane.in","r",stdin);
freopen("alkane.out","w",stdout);
Pre(1e5);
int T,n;
read(T);
while(T--) read(n),write(B[n]),putchar('\n');
}
























 2489
2489











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








