k短路的可持久化可并堆做法

俞鼎力神仙的PPT

传统的 $A^{\ast }$ 算法在图为一个 $n$ 元环的时候每次找一条路都要转整整一圈，复杂度会达到 $O(nk)$
而可持久化可并堆的做法在找路径的时候与 $n$ 无关，找到一条路的复杂度是 $O(\log k)$

定义

在一张有向带权图 $G$ 中，从起点 $s$ 到终点 $t$ 的不严格递增的第 $k$ 短路的长度。两条路径不同定义为按顺序经过的边集不同。

一些性质

记 $dis[i]$ 为 $i$ 到 $t$ 的最短距离，设 $T$ 为以 $t$ 为根用反向边建出的最短路径树。

对于一条起点为 $u$，终点为 $v$，权值为 $w$ 的边 $e$，定义 $\delta (e)=w+di{s}_v-di{s}_u$，表示选择这条边和最短路径的差。

那么对于一条路径 $P$，它的长度 $len(P)=di{s}_s+{\sum }_{e\in P}\delta (e)$

记 $P^{\prime }$ 为路径 $P$ 去掉与 $T$ 的交集后的边集，即路径中的非树边，那么有：

• $P^{\prime }$ 中相邻的两条边 $(a\to b),(c\to d)$，满足 $c$ 是 $b$ 在 $T$ 上的祖先，或 $c=b$。
• 对于不同的路径 $P$，其对应的 $P^{\prime }$ 是唯一的。（树上两点路径是唯一的）
• $len(P)=len(P^{\prime })$ . 因为树边的 $\delta (e)=0$

由后两条性质，$k$ 短路问题可以转化为求前 $k$ 小的 $P^{\prime }$，$P^{\prime }$ 由非树边组成，满足第一条性质。

求解

考虑动态地生成可能的 $P^{\prime }$。
维护一个权值由小到大的优先队列，初始时只有一个空序列。

每次取出队头，即找到的第 $i$ 小的路径，然后在此基础上加入新的非树边。

先考虑朴素的加边方法：
每次从队头取出一个序列 $q$，设 $q$ 的最后一条边的终点为 $v$，加入一条非树边 $e$ 满足 $e$ 的起点是 $v$ 在树上的祖先，一次性将所有可能的边加入。
重复 $k$ 次。
然而每次都将可能的边全部加入显然不现实，复杂度会达到 $O(km\log m)$

注意到一个点拓展出的 $e$ 是有大小顺序的，我们可以每次只拓展 $\delta (e)$ 最小的那条边，与之相应的，要加入“替换最后一条边” 的操作

考虑维护出一个有序表 $g(v)$，按权值由小到大记录所有起点是 $v$ 的祖先的非树边 $e$。
对于每次从队头取出的序列 $q$，设其最后一条边是 $e$，终点为 $v$，倒数第二条边的终点为 $u$，那么有两种产生新的 $P^{\prime }$ 的方式：

• 加入 $g(v)$ 的第一条边
• 将 $e$ 替换为 $g(u)$ 中 $e$ 的后一条边

这样做可以保证取出的队头一定是当前的最小路径，因为所有还未生成的 $P^{\prime }$ 的权值一定大于等于队列中某条路径；并且产生的路径不会重复。
薅一张图：

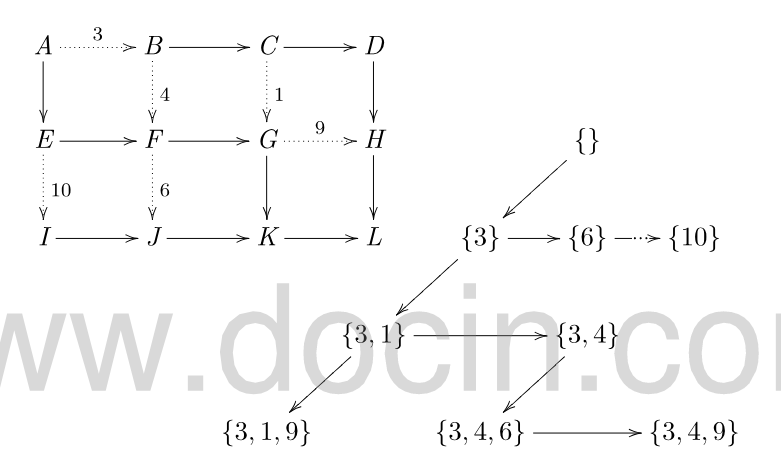
$g(v)$ 显然可以通过 $g(v在树上的父亲)$ 加上所有起点为 $v$ 的非树边得到，于是可以采用可持久化可并堆。

只不过实现上有点讲究，因为我们需要找到 $g(u)$ 中 $e$ 的后一条边，所以实际上一条路径表示为了一个 $pair$，第一维是这条路径的 $\sum \delta (e)$，第二维是这条路径的最后一条边在 $u$ 的堆中的哪个位置。堆里存的是边，键值为 $\delta$ 的大小，要记录边的终点。

那么替换最后一条边就可以表示为将第二维换为堆中它的两个儿子（都要加入），加入一条新边就可以表示为将第二维跳到当前边对应终点的堆顶。

取出 $k$ 次队头即找到了 $k$ 短路。
复杂度 $O(m\log m+k\log k)$

如果把起点为 $v$ 的非树边单独建一个堆，把它当成一个整体元素 $h(v)$，把它插入 $g(v的父亲)$ 得到 $g(v)$，那么建 $h(v)$ 的总复杂度是 $O(m)$（相信大家一定会线性建堆 ），建 $g(v)$ 的总复杂度变为 $O(n\log n)$
只不过替换最后一条边的操作要变成将第二维替换为 $h$ 中的儿子以及 $g$ 中的儿子，在 $k\log k$ 上有个 4 的常数。
于是除去最短路的复杂度是 $O(m+k\log k)$ 的。（虽然最短路一般就是 $O(m\log m)$ …）

例题：洛谷P2483 【模板】k短路 / [SDOI2010]魔法猪学院

Code（此题要求到 $n$ 结束，故将 $n$ 的出边删去）：

#include<bits/stdc++.h>
#define maxn 5005
#define maxm 400005
using namespace std;
const double eps = 1e-8;
int sgn(double x){return fabs(x)>eps?1:0;}
int n,m,ans;
bool vis[maxn],ont[maxm];
int fir[maxn],nxt[maxm],to[maxm],tot=1;
double w[maxm],E,dis[maxn];
void line(int x,int y,double z){nxt[++tot]=fir[x],fir[x]=tot,to[tot]=y,w[tot]=z;}
struct Heap{
	int lc,rc,d,ed;
	double w;
}t[maxm*10]; int rt[maxn],sz;
int New(double w,int ed){return t[++sz]=(Heap){0,0,1,ed,w},sz;}
void merge(int &i,int x,int y){
	if(!x||!y) return void(i=x+y);
	if(t[x].w>t[y].w) swap(x,y);
	t[i=++sz]=t[x],merge(t[i].rc,t[x].rc,y);
	if(t[t[i].lc].d<t[t[i].rc].d) swap(t[i].lc,t[i].rc);
	t[i].d=t[t[i].rc].d+1;
}
typedef pair<double,int> pdi;
priority_queue<pdi,vector<pdi>,greater<pdi> >q;
int QT[maxn],PT,fa[maxn];
void dfs(int u){
	vis[u]=1,QT[++PT]=u;
	for(int i=fir[u],v;i;i=nxt[i]) if(i&1&&!vis[v=to[i]]&&!sgn(dis[u]+w[i]-dis[v]))
		ont[i^1]=1,fa[v]=u,dfs(v);
}
int main()
{
	int x,y; double z;
	scanf("%d%d%lf",&n,&m,&E);
	for(int i=1;i<=m;i++) {scanf("%d%d%lf",&x,&y,&z); if(x==n) {i--,m--;continue;} line(x,y,z),line(y,x,z);}
	memset(dis,68,sizeof dis);
	q.push(pdi(dis[n]=0,n));
	while(!q.empty()){
		int u=q.top().second; double d=q.top().first; q.pop();
		if(sgn(dis[u]-d)) continue;
		for(int i=fir[u],v;i;i=nxt[i]) if(i&1&&dis[v=to[i]]>dis[u]+w[i]+eps)
			q.push(pdi(dis[v]=dis[u]+w[i],v));
	}
	dfs(n);
	for(int i=2;i<=tot;i+=2) if(!ont[i]&&vis[x=to[i^1]]&&vis[y=to[i]]) merge(rt[x],rt[x],New(dis[y]+w[i]-dis[x],y));
	for(int i=1,x;i<=PT;i++) if(fa[x=QT[i]]) merge(rt[x],rt[x],rt[fa[x]]);
	if(dis[1]-eps<=E) E-=dis[1],ans++;
	if(rt[1]) q.push(pdi(t[rt[1]].w,rt[1]));
	while(!q.empty()){
		int u=q.top().second,v; double s=q.top().first; q.pop();
		if(dis[1]+s-eps>E) break;
		E-=dis[1]+s,ans++;
		if(t[u].lc) q.push(pdi(s-t[u].w+t[t[u].lc].w,t[u].lc));
		if(t[u].rc) q.push(pdi(s-t[u].w+t[t[u].rc].w,t[u].rc));
		if(rt[v=t[u].ed]) q.push(pdi(s+t[rt[v]].w,rt[v]));
	}
	printf("%d\n",ans);
}