[Luogu P2279][HNOI 2003] 消防局的设立题解 贪心 / 树形dp

题目描述

洛谷传送门

题目描述
2020年，人类在火星上建立了一个庞大的基地群，总共有n个基地。起初为了节约材料，人类只修建了n-1条道路来连接这些基地，并且每两个基地都能够通过道路到达，所以所有的基地形成了一个巨大的树状结构。如果基地A到基地B至少要经过d条道路的话，我们称基地A到基地B的距离为d。
由于火星上非常干燥，经常引发火灾，人类决定在火星上修建若干个消防局。消防局只能修建在基地里，每个消防局有能力扑灭与它距离不超过2的基地的火灾。
你的任务是计算至少要修建多少个消防局才能够确保火星上所有的基地在发生火灾时，消防队有能力及时扑灭火灾。

输入格式
输入文件的第一行为n （n<=1000），表示火星上基地的数目。接下来的n-1行每行有一个正整数，其中文件第i行的正整数为a[i]，表示从编号为i的基地到编号为a[i]的基地之间有一条道路，为了更加简洁的描述树状结构的基地群，有a[i]<i。

输出格式
输出文件仅有一个正整数，表示至少要设立多少个消防局才有能力及时扑灭任何基地发生的火灾。

样例输入输出

Sample Input
6
1
2
3
4
5
Sample Output
2

题解

贪心解法

解题思路

想要用贪心，就必须满足局部最优性
首先，我们考虑一个节点。对于深度最深的节点u而言（深度最深：方便转移，且可以覆盖所有情况），想要覆盖到它，只能通过三个节点转移：
节点u，节点u的父亲，节点u的祖父

我们分类讨论，
①在u节点设立消防站：

②在u节点的父亲这里消防站：

③在u节点的祖父设立消防站：

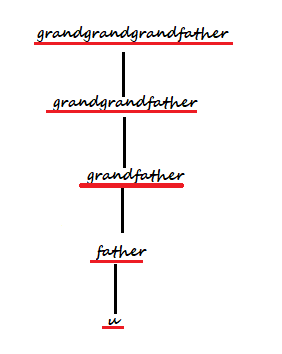
综上，我们可以很容易地得到一个结论：对于任意一个当前是深度最深且未被覆盖的节点而言，选择它的祖父是最优的。

接下来，我们来证明每一步都选择祖父一定是最优的（即，局部最优性）：
首先，我们可以保证没有任何一个节点是不被覆盖的（我们考虑了每一个当前没有被覆盖的节点）；
其次，我们若是选择一个其他的节点，可能会多几个节点（由于某些节点被多覆盖，导致其他节点在相同的消防站数的情况下，没有被覆盖）。
综上，此题具有局部最优性，因此，我们可以大胆采用贪心算法（舍弃七拐八绕的dp做法）

参考代码

#include <cstdio>
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

const int N = 1000;
int n, fa[N + 5], cnt, ans;
bool vis[N + 5], dis[N + 5][3];
vector < int > G[N + 5];
struct node {
	int ip, depth;
	node () {}
	node (const int Ip, const int Depth) {
		ip = Ip;
		depth = Depth;
	}
	
	bool operator < (const node tmp) const {
		return depth > tmp.depth;
	}
}point[N + 5];

void dfs (const int u, const int dep) {
	point[++ cnt] = node(u, dep + 1);
	for (int i = 0; i < G[u].size(); ++ i) {
		int v = G[u][i];
		if (fa[v])
			continue;
		fa[v] = u;
		dfs (v, dep + 1);
	}
}

queue < node > q;
void bfs (const int s) {
	q.push( node (s, 0) );
	dis[s][0] = true;
	vis[s] = true;
	while (! q.empty()) {
		node u = q.front();
		q.pop();
		if (u.depth == 2)
			continue;
		
		for (int i = 0; i < G[u.ip].size(); ++ i) {
			int v = G[u.ip][i];
			if (dis[v][u.depth + 1])
				continue;
			dis[v][u.depth + 1] = true;
			vis[v] = true;
			q.push( node (v, u.depth + 1) ); 
		}
	}
}

int main () {
	scanf ("%d", &n);
	for (int i = 2; i <= n; ++ i) {
		int v;
		scanf ("%d", &v);
		G[i].push_back( v );
		G[v].push_back( i );
	}
	
	fa[1] = 1;
	dfs (1, 0);
	sort (point + 1, point + cnt + 1);
	
	for (int i = 1; i <= n; ++ i) {
		if (vis[point[i].ip])
			continue;
		++ ans;
		bfs (fa[fa[point[i].ip]]);
	}
	printf ("%d\n", ans);
	return 0;
}

dp解法

解题思路

上面说了，dp算法有点绕 (反正本蒟蒻是这么认为的。。。) ，我只能尽量说清楚。。。

首先给出dp[i][j]以及son[i][j]的定义：dp[i][j]表示以节点i为根的子树还有得救，并且还可以向上救i个节点的最小花费；son[i][j]表示节点i向下j层及以下的还有得救的最小花费（不包含节点i，即：son[i][0]表示节点i的所有儿子，son[i][1]表示节点i的所有孙子，以此类推）。
有了定义，我们就可以开始进一步的思考：如果我们考虑一条单链，要节点u还有得救，那么易得，最近的一个消防站能覆盖到的最远的节点和u的距离不超过4（当且仅当消防站建在u节点的祖父或孙子节点），即：最多有5个节点（参考下图）

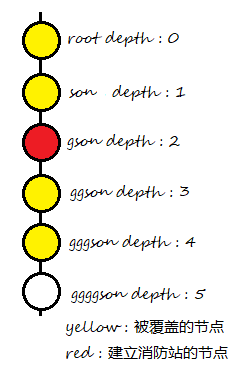
由此，我们可以看出dp[i][j]中的第二维只需要从0考虑到2即可，son[i][j]中的第二维只需要考虑0和1即可。
接下来，我们开始写状态转移方程式（结合图像理解，略有些凌乱，望理解）

---

以下的状态转移方程时中要注意dp[son1][0] 与 son[son1][0]的区别（前者是一群已经算过的子树，后者是一颗以son2为根的子树），以及诸如此类的
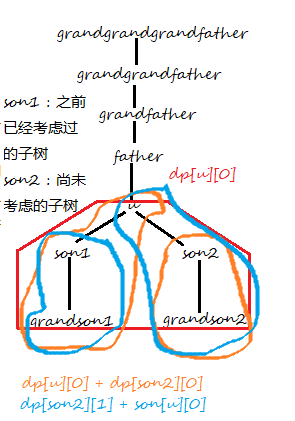
①.考虑dp[u][0]的转移：

$$dp[u][0]=min(dp[u][0]+dp[son2][0],dp[son2][1]+son[u][0])$$
②.考虑dp[u][1]的转移：

$$dp[u][1]=min(dp[u][1]+son[son2][0],dp[son2][2]+son[u][1])$$
这里的转移不考虑节点son2的原因是，由于当前情况必须要覆盖节点father，那么消防站就必须建在节点u或是节点u的儿子一层（集合表示为son1），因此节点son2是一定可以被覆盖到的；由于通过很简单的逻辑推理可以知道，取dp[son2][0]一定不比取son[son2][0]小，为了选择最优，我们才有了上述的状态转移方程式
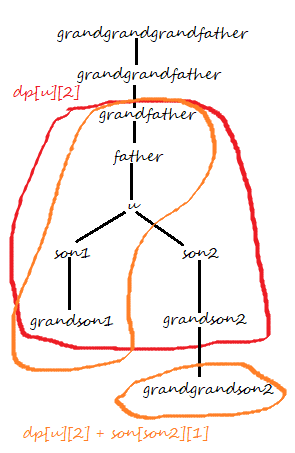
③.考虑dp[u][2]的转移：

$$dp[u][2]=dp[u][2]+son[son2][1]$$
在取转移状态时，不考虑son2和grandson2的原因与第二种情况类似。在这种情况下，为了覆盖到grandfather这个节点，我们必须将消防站建立在节点u的位置，因此，是一定可以覆盖到以son2和grandson2为代表的一群节点。

④考虑son[u][0]的转移，多了一颗以son2为根的子树，因此，只需累加dp[son2][0]即可
⑤考虑son[u][1]的转移，多了一颗以grandson2为根的子树，因此，只需累加son[son2][0]即可
$$son[u][0]=son[u][0]+dp[v][0];$$
$$son[u][1]=son[u][1]+son[v][0];$$

既然已经知道了状态转移方程式，那么就可以开始码代码了（由于是通过儿子节点转移的，因此要回溯后转移）

参考代码

#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;

const int N = 1000;
int n, dp[N + 5][3], son[N + 5][2];
bool vis[N + 5];
vector < int > G[N + 5];

void sovle (const int u) {
	dp[u][0] = dp[u][1] = dp[u][2] = 1;
	son[u][0] = son[u][1] = 0; vis[u] = true;
	for (int i = 0; i < G[u].size(); ++ i) {
		int v = G[u][i]; 
		if (vis[v])
			continue;
		sovle (v);
		dp[u][0] = min ( dp[u][0] + dp[v][0], dp[v][1] + son[u][0] );
		dp[u][1] = min ( dp[u][1] + son[v][0], dp[v][2] + son[u][1] );
		dp[u][2] += son[v][1];
		son[u][0] += dp[v][0];
		son[u][1] += son[v][0];
		
		dp[u][1] = min (dp[u][1], dp[u][2]);
		dp[u][0] = min (dp[u][0], dp[u][1]);
		son[u][0] = min (son[u][0], dp[u][0]);
		son[u][1] = min (son[u][1], son[u][0]);
	}
}

int main () {
	scanf ("%d", &n);
	for (int i = 2; i <= n; ++ i) {
		int v;
		scanf ("%d", &v);
		G[i].push_back( v );
		G[v].push_back( i );
	}
	
	sovle (1);
	printf ("%d\n", dp[1][0]);
	return 0;
}

后记

对于树上dp的做法，还有不同的理解方式（大多数博客所写的方式），大同小异，感兴趣的童鞋们可以去看看，在洛谷题解区有很多解题报告，详情戳→_→这里