简单の暑假总结——图论基础

4.1 图论概念

图论是一个极为重要的知识点，我们需要一些篇幅去介绍它

本篇主要是一些基础知识

图的概念很多，听我细细道来

4.1.1 什么是图

截至目前，我们主要学了 $3$ 种数据结构（不含图）

1. 集合（变量应该算吧）

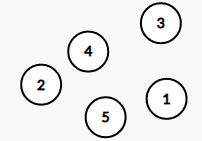
就是一群散点，元素与元素间没有什么联系

2. 线性表（数组，队列，栈……）

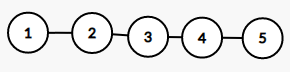
如图，它们所组成的结构类似一条线，因此被称为线性结构

3. 树形结构

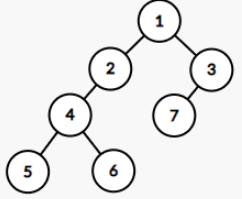
如图，这种结构长的像颗树，因此被称为树形结构

好吧我也不知道为啥叫树形结构

那么，图应该是我们所学的第 $4$ 种数据结构了

4. 图

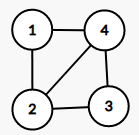
那么，我们现在要给图下一个定义了

很简单，点用边连起来就叫做图，严格意义上讲，图是一种数据结构，定义为 $graph=(V,E)$ .$V$ 是一个非空优先集合，代表顶点（结点）， $E$ 代表边的集合。——《一本通》

图（Graph） 描述的是一些个体之间的关系。和线性表和二叉树不同的是：这些个体之间既不是前驱后继的顺序关系，也不是祖先后代的层次关系，而是错综复杂的网状关系。——《算法经典》

其实，我们只需要知道：

1. 图描述的是各个元素之间的关系（废话）
2. 图的关系很复杂

特殊的，线性表和树形结构也是一种图

4.1.2 图的分类

图分为三类：无向图，有向图和带权图

4.1.2.1 无向图

顾名思义，一个没方向的图，即边没有指定方向的图

举个栗子：在下图就有一张无向图

那么，对于无向图，下面有一些术语（一般来讲，xie’e的出题人会直接在题干中使用术语，请务必理解）：

在无向图中，如果两个顶点之间有边连接，那么就视为两个顶点相邻。

举个栗子：在上图中，我们可以认为 $1$ 号结点和 $2$ 号结点相邻，但 $1$ 号结点和第 $3$ 号结点不相邻

那么，对于相邻顶点的序列，我们将其称为路径

举个栗子：在上图中，我们可以认为 $1-2-3-4$ 是一条路径

特殊的：起点和终点重合的路径叫做圈（毕竟长的像）

举个栗子：在上图中，我们可以认为 $1-2-3-4-1$ 是一个圈

对于一个单个顶点，该顶点连接的边数叫做该顶点的度

举个栗子：在上图中，我们可以认为 $1$ 号结点的度为 $2$ ，而 $2$ 号结点的度为 $3$

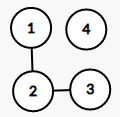
对于各种类型的图而言，任意两点之间都有路径连接的图称为连通图，反之，称为非连通图

举个栗子：上图就是连通图，而下图则是非连通图

这里，教一个装B的小技巧

我们可以将树称为没有圈的连通图，森林称为没有圈的非连通图

结合树的定义，应该好理解吧？

主要是我也不想写

4.1.2.2 有向图

顾名思义，一个有方向的图，即边有指定方向的图

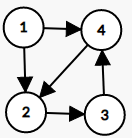
特殊的：有向图中的边又称为弧，起点称为弧头，终点称为弧尾

那么，对于有向图，下面有一些术语：

在有向图中，边是单向的：每条边所连接的两个顶点之间的邻接性是单向的。

举个栗子：在上图中，我们可以认为 $1$ 号结点和 $2$ 号结点相邻 ，但 $2$ 号结点不和 $1$ 号结点相邻

那么，对于相邻顶点的序列，我们将其称为有向路径

举个栗子：在上图中，我们可以认为 $1-2-3-4$ 是一条有向路径

特殊的：一条至少含有一条边且起点和终点相同的有向路径叫做有向环

举个栗子：在上图中，我们可以认为 $2-3-4-2$ 是一条有向环

注意：为什么定义里会说至少含有一条边呢？路径不应该是两条起步吗？

对于一些聪（hun）明（zhang）出题人，可能会出现这样的图：

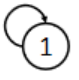
是的，自己连自己！

在这种情况下，我们也认为这是一个有向环

特殊的：我们把没有环的有向图称为有向无环图（DAG）

举个栗子：下图就是一个 DAG

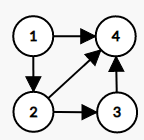
Tips：在题目中，出题人可能会直接写 DAG ，而非有向无环图

在有向图中，度被分为了入度和出度

通俗来讲，一个顶点的入度指最终指向该顶点的边的数量，出度指从该顶点指出去的边的数量

举个栗子：在上图中，我们可以认为 $2$ 号结点的入度为 $1$ ，而 出度为 $2$

4.1.2.3 带权图

带权图，指边上带有权值的图（不同问题中，权值意义不同，可以是距离、时间、价格、代价等）

下图就是一张带权图

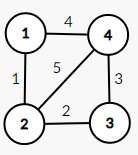
关于带权图，暂时不需要介绍术语，掌握无向图和有向图的术语即可

4.2 图的存储方式

图的存储方式常见的有三种：邻接矩阵，邻接表和链式前向星

4.2.1 邻接矩阵

个人认为邻接矩阵是最简单的一种存储图的方式

对于有 $n$ 个顶点的图，我们可以采用 $flag[n][n]$ 这样一个数组来表示它

具体含义：若 $flag[i][j]=1$ 说明 $i$ 和 $j$ 之间有一条连线； 若 $flag[i][j]=0$ 说明 $i$ 和 $j$ 之间没有一条连线

特殊的：在无向图中， $flag[i][j]=flag[j][i]$

举个栗子：

在上图中，如果我们用一张表来表示 $flag$ 数组，应该是如下图所示：

$\left[\begin{array}{ccccc}\mathrm{NULL}& j=1& j=2& j=3& i=4\\ i=1& 0& 1& 0& 1\\ i=2& 1& 0& 1& 1\\ i=3& 0& 1& 0& 1\\ i=4& 1& 1& 1& 0\end{array}\right]$

同样，有向图和带权图也能用邻接矩阵来表示：

对于上图的有向图，$flag$ 数组如下图所示：

$\left[\begin{array}{ccccc}\mathrm{NULL}& j=1& j=2& j=3& j=4\\ i=1& 0& 1& 0& 1\\ i=2& 0& 0& 1& 1\\ i=3& 0& 0& 0& 1\\ i=4& 0& 0& 0& 0\end{array}\right]$

在有向图的邻接矩阵中：顶点 $i$ 的出度为：第 $i$ 行所有非零元素的个数

显然，因为在有向图的邻接矩阵中， $flag[i][j]$ 表示以 $i$ 为起点， $j$ 为终点，是否存在一条边，则第 $i$ 行所有非零元素的个数就代表有多少个点从第 $i$ 号点出发的，即 $i$ 号点的出度

同理可得：在有向图的邻接矩阵中：顶点 $i$ 的入度为：第 $i$ 列所有非零元素的个数

考虑一个带权图：

在上图中，如果我们用一张表来表示 $flag$ 数组，应该是如下图所示：

$\left[\begin{array}{ccccc}\mathrm{NULL}& j=1& j=2& j=3& j=4\\ i=1& \infty & 1& \infty & 4\\ i=2& 1& \infty & 2& 5\\ i=3& \infty & 2& \infty & 3\\ i=4& 4& 5& 3& \infty \end{array}\right]$

其中如果 $flag[i][j]=\infty$ 就说明 $i$ 号顶点和 $j$ 号顶点间不存在一条边；反之，说明 $i$ 号顶点和 $j$ 号顶点间存在一条边，并用 $flag[i][j]$ 记录其边权

Eg_1 邻接矩阵存储图

这是一道裸题

#include<cstdio>
#include<algorithm>
using namespace std;
bool a[2005][2005];			//邻接矩阵
int main(){
	int n,m,x,y;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		a[x][y]=a[y][x]=1;			//因为是无向图，所以需要双向存边
	}
	for(int i=1;i<=n;i++){			//一次枚举每个点
		for(int j=1;j<=n;j++){
			if(a[i][j]==1){			//判断是否有边相连
				printf("%d ",j);
			}
		}
		printf("\n");
	}
	return 0;
}

在用邻接矩阵存储图中，我们可以 $O(1)$ 的时间复杂度判断 $i$ 与 $j$ 之间是否有边相连，但是，如果我们存储的是一个稀疏图（点多边少的图），就十分浪费空间，而且，在查找最短路中，也很浪费时间

所以，我们需要另外的方法存储图

4.2.2 邻接表

邻接表是最常用的存储图的方式，也是链式前向星的基础，相当重要

我们一般通过链表的方式（即使用不定长数组）实现邻接表

当然，由于我对结构体深沉的爱，我一般是通过结构体

以下有关邻接表的做法全部是通过结构体实现的，如果你不想看，Go to here

在结构体中 $a[i]$ 中，可以定义一个 $len$ 变量和一个 $sum$ 数组，其中，用 $sum$ 数组来表示与第 $i$ 号元素所相邻的元素， $len$ 表示 $sum$ 数组的长度，即有多少个元素与第 $i$ 号元素相邻

举个栗子：

如果我们要通过邻接表来存储上图，那么，实现结果应如下图所示：

a [   1   ] . l e n = 2 , a [   1   ] . s u m [   2   ] = { 2 , 4 } a [   2   ] . l e n = 3 , a [   2   ] . s u m [   3   ] = { 1 , 3 , 4 } a [   3   ] . l e n = 2 , a [   3   ] . s u m [   2   ] = { 2 , 4 } a [   4   ] . l e n = 3 , a [   4   ] . s u m [   3   ] = { 1 , 2 , 3 } a[\ 1\ ].len=2,a[\ 1\ ].sum[\ 2\ ]=\{2,4\}\\a[\ 2\ ].len=3,a[\ 2\ ].sum[\ 3\ ]=\{1,3,4\}\\a[\ 3\ ].len=2,a[\ 3\ ].sum[\ 2\ ]=\{2,4\}\\a[\ 4\ ].len=3,a[\ 4\ ].sum[\ 3\ ]=\{1,2,3\} a[ 1 ].len=2,a[ 1 ].sum[ 2 ]={2,4}a[ 2 ].len=3,a[ 2 ].sum[ 3 ]={1,3,4}a[ 3 ].len=2,a[ 3 ].sum[ 2 ]={2,4}a[ 4 ].len=3,a[ 4 ].sum[ 3 ]={1,2,3}

用邻接表存储有向图的方法与存储无向图的方法大同小异，不再赘述

那么，如果我们要存储一个带权图呢？

那么，我们就需要将 $a$ 数组里的 $sum$ 数组定义成结构体数组（恐怕只有我这种天才才想得出结构体套结构体的做法吧？）

那么，在 $sum[i]$ 中，我们包含了两个信息：$sum$ 和 $num$ ，其中， $num$ 表示当前元素的下标， $sum$ 表示该元素与第 $i$ 号元素的权值

再举一个栗子：

如果我们要通过邻接表来存储上图，那么，实现结果应如下图所示：

a [   1   ] . l e n = 2 , a [   1   ] . s u m [   2   ] . n u m = { 2 , 4 } ,      a [   1   ] . s u m [   2   ] . s u m = { 1 , 4 } a [   2   ] . l e n = 3 , a [   2   ] . s u m [   3   ] . n u m = { 1 , 3 , 4 } , a [   2   ] . s u m [   3   ] . s u m = { 1 , 2 , 5 } a [   3   ] . l e n = 2 , a [   3   ] . s u m [   2   ] . n u m = { 2 , 4 } ,      a [   3   ] . s u m [   2   ] . s u m = { 2 , 3 } a [   4   ] . l e n = 3 , a [   4   ] . s u m [   3   ] . n u m = { 1 , 2 , 3 } , a [   4   ] . s u m [   3   ] . s u m = { 4 , 5 , 3 } a[\ 1\ ].len=2,a[\ 1\ ].sum[\ 2\ ].num=\{2,4\},\ \ \ \ a[\ 1\ ].sum[\ 2\ ].sum=\{1,4\}\\a[\ 2\ ].len=3,a[\ 2\ ].sum[\ 3\ ].num=\{1,3,4\},a[\ 2\ ].sum[\ 3\ ].sum=\{1,2,5\}\\a[\ 3\ ].len=2,a[\ 3\ ].sum[\ 2\ ].num=\{2,4\},\ \ \ \ a[\ 3\ ].sum[\ 2\ ].sum=\{2,3\}\\a[\ 4\ ].len=3,a[\ 4\ ].sum[\ 3\ ].num=\{1,2,3\},a[\ 4\ ].sum[\ 3\ ].sum=\{4,5,3\} a[ 1 ].len=2,a[ 1 ].sum[ 2 ].num={2,4},    a[ 1 ].sum[ 2 ].sum={1,4}a[ 2 ].len=3,a[ 2 ].sum[ 3 ].num={1,3,4},a[ 2 ].sum[ 3 ].sum={1,2,5}a[ 3 ].len=2,a[ 3 ].sum[ 2 ].num={2,4},    a[ 3 ].sum[ 2 ].sum={2,3}a[ 4 ].len=3,a[ 4 ].sum[ 3 ].num={1,2,3},a[ 4 ].sum[ 3 ].sum={4,5,3}

Eg_2 邻接表存储图

邻接点按照度数由小到大输出,如果度数相等，则按照编号有小到大输出。

右上，我们还需要在 $a$ 数组中添加一个信息： $size$ ，表示度数

具体详情见代码：

#include<cstdio>
#include<algorithm>
using namespace std;
struct node{
	int sum[1005],len,size;
}a[1005];
bool cmp(int x,int y){			//排序，以度数为第一关键字，数值为第二关键字
	if(a[x].size!=a[y].size){
		return a[x].size<a[y].size;
	}
	return x<y;
}
int main(){
	int n,m,x,y;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		a[x].len++;
		a[x].sum[a[x].len]=y;			//处理新增的与第 i 号点连接的点
		a[x].size++;			//处理度数
		a[y].len++;
		a[y].sum[a[y].len]=x;
		a[y].size++;			//无向图，双向处理
	}
	for(int i=1;i<=n;i++){
		sort(a[i].sum+1,a[i].sum+1+a[i].len,cmp);			//排序
		for(int j=1;j<=a[i].len;j++){
			printf("%d ",a[i].sum[j]);			//输出
		}
		printf("\n");
	}
	return 0;
}

4.2.3 链式前向星

上文已提，真正的邻接表是由不定长数组实现的，而链式前向星则是由数组

具体详情Go to here

其实我也不太懂链式前向星，不敢瞎BB

4.3 图的遍历

图的遍历有两种：DFS和BFS

如果就这还要详细讲解，你可以回家种田了

这里，在此给大家推荐一个强大的网址：

程序可视化

这是一个强大的网站，大家可以自行探索

我真的不是不想写！

那么，我们来看两道例题：

Eg_3 有向图的DFS

数据范围不大，可以采用邻接矩阵输入，操作起来也方便

注意：这里是有向图，不是无向图

#include<cstdio>
bool a[205][205];
bool flag[205];
int n,m,x,y;
void dfs(int num){
	printf("%d ",num);
	flag[num]=1;			//标记为已遍历
	for(int i=1;i<=n;i++){			//要求字典序最小，所以要按照顺序
		if(a[num][i]==1&&flag[i]==0){			//如果两点之间有边连接且第 i 好点未被遍历
			dfs(i);			//遍历
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		a[x][y]=1;			//建图
	}
	for(int i=1;i<=n;i++){			//要求字典序最小，所以要按照顺序
		if(flag[i]==0){			//注意：这里不一定是连通图，所以，凡是还没有被遍历到的都要在进行一次DFS
			dfs(i);
		}
	}
	return 0;
}

Eg_4 有向图的BFS

#include<queue>
#include<cstdio>
using namespace std;
bool a[205][205];
bool flag[205];
int n,m,x,y;
void bfs(int num){
	printf("%d ",num);			//输出当前元素
	flag[num]=1;
	queue<int> q;
	q.push(num);
	while(!q.empty()){
		int xx=q.front();
		q.pop();			//以上为BFS基本操作
		for(int i=1;i<=n;i++){
			if(a[xx][i]&&!flag[i]){			//如果两点间有边连接且第 i 号点未被遍历
				q.push(i);
				printf("%d ",i);
				flag[i]=1;			//标记，输出，压队列
			}
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		a[x][y]=1;			//采用邻接矩阵建图
	}
	for(int i=1;i<=n;i++){			//与上题类似
		if(flag[i]==0){			//与上题相类似，要考虑非连通图
			bfs(i);
		}
	}
	return 0;
}

栗子：你在这篇文章中一共举了我 $14$ 次，你礼貌吗？