线性DP三大基本模型

在线性 DP 中，我们会遇到各种各样的问题，而这些问题的解法或解题思路大多都与线性 DP 三大基本模型相关，分别是最长上升子序列，最长公共子序列，最长公共上升子序列

1. 最长上升子序列（LIS）

定义状态：

dp[i]表示以序列的第 $i$ 位结尾的 LIS

很显然，在处理dp[i]时，如果序列的第 $j(1\le j<i)$ 小于 第 $i$ 位，说明是满足更新 LIS 的条件的，此时，如果dp[j]+1（加上的 $1$ 是序列的第 $i$ 位）大于dp[i]，选择更新

即状态转移方程式为：

d p [   i   ] = max ⁡ { d p [   j   ] + 1 }   ( 1 ≤ j < i   and ⁡   a [   j   ] < a [   i   ] ) dp[\ i\ ]=\max\{dp[\ j\ ]+1\}\ (1\le j<i\ \operatorname{and}\ a[\ j\ ]<a[\ i\ ]) dp[ i ]=max{dp[ j ]+1} (1≤j<i and a[ j ]<a[ i ])

以此类推，还有最长不上升子序列，最长下降子序列等变种，做法大同小异

1.1. 输出 LIS

首先，我们要理解一下状态转移方程式的含义

如果我们用dp[j]更新了dp[i]，就相当于对应了上升序列 $(x,y,z,\cdots ,a[j])$ 后面接上了 $a[i]$ ，即序列变为了 $(x,y,z,\cdots ,a[j],a[i])$

换言之，如果用dp[j]更新了dp[i]，那么此时dp[i]所对应的上升序列中，a[i]的前驱为a[j]

所以，每一次更新时，我们在将其对应的前驱pre[i]也进行修改，最后通过前驱输出序列即可

代码：

#include<cstdio>
#include<algorithm>
using namespace std;
int n,dp[5005],pre[5005],a[5005],ans,ans_i;
void print(int num){
	if(pre[num]!=num){			//当前元素非一号元素
		print(pre[num]);			//先输出前面的所有数
	}
	printf("%d ",a[num]);			//输出自己
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	for(int i=1;i<=n;i++){
		int sum=0,tot=i;			//sum 最后用于更新 dp[i] ，tot 用于更新前驱 pre[i]
		for(int j=1;j<i;j++){
			if(a[j]<a[i]&&sum<dp[j]){			//满足更新条件且有价值更新
				sum=dp[j],tot=j;			//更新
			}
		}
		pre[i]=tot,dp[i]=sum+1;			//赋值
	}
	for(int i=1;i<=n;i++){			//找到最优的上升序列
									//在上文定义的状态中，不能保证 dp[n] 最优
									//对于序列 1 1 4 5 1 4 而言，dp[6]=2,dp[4]=2
		if(dp[i]>ans){
			ans=dp[i];
			ans_i=i;
		}
	}
	printf("%d\n",ans);			//输出长度
	print(ans_i);			//输出序列
	return 0;
}

1.2. 优化算法

可以发现，上述求 LIS 的时间复杂度为 $O(n^2)$ ，有没有更快的做法呢？

我们可以在创立一个数组b，其中b[i]表示原序列中长度为 $i$ 的 LIS 的最后一位的最小值，同时创建一个变量len，表示b数组里的有效元素的个数

首先，本着贪心的原则，当b[i]尽可能小的时候，后面所接上来的元素就会更多，所得到的 LIS 的长度也就越大

有了这样的一个贪心想法，我们来思考一下b数组的更新方法

1. b[len]<a[i]

我们现在所得的 LIS 的最后一位是b[len]，现在出现了比它更大的数，自然，开开心心的将a[i]赋值给b[++len]

2. b[len]>=a[i]

此时，我们肯定是要更新b数组了，如何更新？

先考虑这样的一个结论：

在b数组中， $\forall i,j\in {\mathbb{Z}}^{+},i<j,b[i]<b[j]$（即b数组单调递增）

这个结论很好想，假如存在 b[i]>=b[j] 的情况，那么b[i]所存储的值必然不是最优的，至少，在b[j]所对应的长度为 $j$ 的上升序列中，还必存在 LIS[i]<b[i]

所以，在更新b数组时，我们选择第一个满足b[k]<a[i]&&a[i]<=b[k+1]的k，使b[k+1]=a[i]

由于b数组单调递增，所以我们可以用二分的方法来找到k，或者，使用lower_bound也是可以的

代码：

#include<cstdio>
#include<algorithm>
using namespace std;
int a[100005],len,x,n;
int main(){
	scanf("%d",&n);
	a[0]=-2147483647;			//预处理最小值
	for(int i=1;i<=n;i++){
		scanf("%d",&x);
		if(a[len]<x){			//处理第一种情况
			a[++len]=x;
		}else{			//处理第二种情况
			a[lower_bound(a+1,a+1+len,x)-a]=x;
		}
	}
	printf("%d",len);
	return 0;
}

时间复杂度 $O(n\log n)$

顺带一提：似乎用优化后的算法不能准确输出最长上升子序列

1.3. 习题选讲

题目：友好城市

首先，我们以样例来举个例子：

如上图所示，这就是我们所得到的样例（画的是真的丑）

我们用二元组 $(a_i,b_i)$ 来表示一条线段

显然，我们需要将二元组的某一项升序排序，这里选择对 $a_i$ 进行升序排序

现在，我们来思考，选择什么样的线段能满足其两者之间互不相交

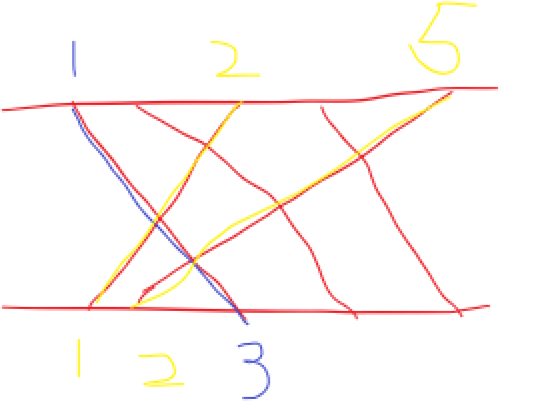
假设我们选择了蓝色线段 $(1.3)$ ，那么，我们就不能选择黄色线段 $(2,1),(5,2)$

我们观察这三个二元组，发现： 所选择的蓝色线段的二元组的 $a_i$ 项小于黄色线段的 $a_i$ 项，蓝色线段的二元组的 $b_i$ 项大于黄色线段的 $b_i$ 项

由此得出猜想：对于最终所选的若干条线段中，$\forall i,j\in {\mathbb{Z}}^{+},a_i<a_j,b_i\ngtr b_j,\text{即}{b}_i<b_j(\text{此处不存在}{b}_i=b_j\text{的情况})$

这个结论应该是显然的，如果 $a_i<a_j$ ，那么若要使得第 $i$ 条线段的第 $j$ 条线段不产生交点，那么 $b_j$ 必须在 $b_i$ 的右边，即 $b_i<b_j$

同理，我们可以推得类似的结论：$\forall i,j\in {\mathbb{Z}}^{+},a_i>a_j,b_i\nless b_j,\text{即}{b}_i>b_j$

而 $a_i$ 已经进行了升序排序，那么此时，根据上面推得的结论，我们只需要求出 $b_i$ 的最长上升子序列即可

代码：

#include<cstdio>
#include<algorithm>
using namespace std;
int n,ans;
struct node{
	int x,y;
	bool operator<(const node other){
		return x<other.x;
	}
}a[5005];
int dp[5005];
int main(){
	scanf("%d%d%d",&n,&n,&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&a[i].x,&a[i].y);
	}
	sort(a+1,a+1+n);			//对二元组的 a 项升序排列
	for(int i=1;i<=n;i++){			//求 b 项的 LIS
		int sum=0;
		for(int j=1;j<i;j++){
			if(a[i].y>a[j].y&&sum<dp[j]){
				sum=dp[j];
			} 
		}
		dp[i]=sum+1;
		ans=max(ans,dp[i]);
	} 
	printf("%d",ans);			//输出
	return 0;
}

2. 最长公共子序列（LCS）

定义状态：

dp[i][j]表示由 $a$ 序列的前 $i$ 项和 $b$ 序列的前 $j$ 项所组成的 LCS 的长度

显然，我们要分两种情况：

1. a[i]==b[j]

这种情况下，显然，a[i]和b[j]肯定是要做贡献的，所以，我们可以让dp[i-1][j-1]（在不考虑a[i]和b[j]的情况下）的值加上 $1$ （考虑a[i]和b[j]后），就得到了dp[i][j]的结果

2. a[i]!=b[j]

这种情况下，显然，a[i]和b[j]中至少有一个做不了贡献，此时，如果让a[i]不做贡献，则dp[i][j]=dp[i-1][j]，如果让b[j]不做贡献，则dp[i][j]=dp[i][j-1]，两者比一个max即可

即状态转移方程式为：

$$dp[i][j]=\{\begin{array}{ll}dp[i-1][j-1]+1& a[i]=b[j]\\ dp[i][j-1]& a[i]\ne b[j]\mathrm{and}dp[i][j-1]>dp[i-1][j]\\ dp[i-1][j]& a[i]\ne b[j]\mathrm{and}dp[i][j-1]<dp[i-1][j]\end{array}$$

2.1. 输出 LCS

和输出 LIS 的方法大同小异，整一个前缀数组pre[i][j]即可

观察上面的状态转移方程式，dp[i][j]实际上有三种可能的取值，如果是dp[i][j]=dp[i-1][j-1]+1，则pre[i][j]=1；如果是dp[i][j]=dp[i][j-1]，则pre[i][j]=2；如果是dp[i][j]=dp[i][j-1]，则pre[i][j]=3

在处理输出时，如果pre[i][j]==2||pre[i][j]==3，直接往前走即可，反之，说明有字符是做出了贡献，就不要忘了在最后输出这个字符

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
char a[1005],b[1005];
int dp[1005][1005],n,m;
int pre[1005][1005];
void print(int n,int m){
	if(!n||!m){			//至少有一个字符串已经找完了
		return ;
	}
	if(pre[n][m]==1){			//三种情况，注意一一对应
		print(n-1,m-1);
		printf("%c",a[n]);
	}else if(pre[n][m]==2){
		print(n,m-1);
	}else{
		print(n-1,m);
	}
}
int main(){
	scanf("%s%s",a+1,b+1);
	n=strlen(a+1),m=strlen(b+1);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i]==b[j]){			//三种情况上文已提，处理 dp[i][j] 和 pre[i][j]
				dp[i][j]=dp[i-1][j-1]+1;
				pre[i][j]=1;
			}else if(dp[i][j-1]>dp[i-1][j]){
				dp[i][j]=dp[i][j-1];
				pre[i][j]=2;
			}else{
				dp[i][j]=dp[i-1][j];
				pre[i][j]=3;
			}
		}
	}
	printf("%d\n",dp[n][m]);			//输出长度
	print(n,m);			//输出序列
	return 0;
}

2.2. 习题选讲

题目：【模板】最长公共子序列

初看这道题，你或许会震惊：

对于 $100\%$ 的数据， $n\le 10^5$

可是刚才所讲的算法是 $O(n^2)$ ，难不成还有 $O(n\log n)$ 的算法

确实，对于一般的序列求 LCS 而言，应该没有 $O(n\log n)$ 的算法，可是，这道题的序列有一个特殊性质

给出 $1,2,\dots ,n$ 的两个排列 $P_1$ 和 $P_2$

我们发现： $P_1,P_2$ 两个序列是 $1,2,\dots ,n$ 的两个不同的全排列

基于此，我们可以转换一下：

以样例为例：

3 2 1 4 5
1 2 3 4 5

我们用 $A$ 代替 $a_1$ ， $B$ 代替 $a_2$ ，以此类推

得到结果如下：

A B C D E
C B A D E

在将 $A$ 转换成 $1$ ， $B$ 转换成 $2$ ，以此类推

得到结果如下：

1 2 3 4 5
3 2 1 4 5

如果最后的得到的 $c$ 序列是求得的 LCS ，那么 $c$ 序列一定是单调递增（观察转换后的 $P_1$ 序列可得），那么， $c$ 序列在转换后的 $P_2$ 序列中也应该是单调递增的，即： $c$ 序列在转换后的 $P_2$ 序列中是它的 LIS

这样一来，问题就简简单单了

代码：

#include<cstdio>
#include<algorithm>
using namespace std;
int n;
int a[100005],b[100005];
int m[100005];			//转换 P_2 数组时使用的中间数组
int k[100005],len;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		m[a[i]]=i;			//一一对应每一个值
	} 
	for(int i=1;i<=n;i++){
		scanf("%d",&b[i]);
	}
	for(int i=1;i<=n;i++){
		b[i]=m[b[i]];			//转换
	}
	k[0]=-2147483647;			//O(n log n) 求 LIS
	for(int i=1;i<=n;i++){
		if(k[len]<b[i]){
			k[++len]=b[i];
		}else{
			k[lower_bound(k+1,k+1+len,b[i])-k]=b[i];
		}
	}
	printf("%d",len);			//输出
	return 0;
}

当然，对于这种 $O(n\log n)$ 算法，仅适用于这种特殊情况，因为如果 $P_1$ 是 { 1 , 2 , 1 } \{1,2,1\} {1,2,1} 的这种格式，那么，更新后的 $P_1$ 不一定是单调递增的，也就不能使用这种算法

3. 最长公共上升子序列（LCIS）

最后一个模型

首先，定义状态：

dp[i][j]表示 $a$ 字符串选前 $i$ 项， $b$ 字符串选前 $j$ 项，同时b[j]必选的情况总数

显然，对于a[i]而言，我们有选与不选两种情况，分类讨论：

1. 不选择a[i]

显然，不选择a[i]时，dp[i][j]=dp[i-1][j]

2. 选择a[i]

注意：在处理选择a[i]的时候，必须满足a[i]==b[j]，因为b[j]是必选的

选择了a[i]和b[j]后，处理一个用于寻找前驱的循环，找到一个b[k]<b[j]的情况，说明第 $k$ 项可以作为第 $j$ 项的前驱，考虑更新

代码：

#include<cstdio>
#include<algorithm>
using namespace std;
int n,ans;
int a[3005],b[3005];
int dp[3005][3005];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	for(int i=1;i<=n;i++){
		scanf("%d",&b[i]);
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			dp[i][j]=dp[i-1][j];			//不选择 a[i]
			if(a[i]==b[j]){			//满足选择 a[i] 的条件
				for(int k=1;k<j;k++){			//找前驱
					if(b[k]<b[j]){			//找到了满足条件的前驱
						dp[i][j]=max(dp[i][j],dp[i-1][k]+1);			//比较更新
					}
				}
			}
		}
	}
	for(int i=1;i<=n;i++){			//枚举 b[i] ，找最大值
		ans=max(ans,dp[n][i]);
	}
	printf("%d",ans);
	return 0;
}

可惜，代码是 $O(n^3)$ ，能不能再优化一层呢？

3.1. 优化算法

不难发现，最外层的两层循环是省不了的，考虑处理第三层循环

不难发现，第三层循环的作用就是在寻找最大的dp[i-1][k]，但是，由于 $i$ 在进行第三层循环时是保持相对静止的，所以，我们可以选择用一个变量sum来存储目前找到的最大的dp[i-1][k]

由于在上述的代码中，判断b[k]<b[j]是在a[i]==b[j]的情况下进行的，所以，判断条件亦可写成b[k]<a[i]，这方便我们接下来的优化

因为sum是存储的最大值，所以，当a[i]==b[j]时，直接用sum进行最大值的比较就行了；当a[i]>b[j]时，说明此时sum是满足更新条件的，考虑是否更新

所以，我们就巧妙地省去了第三层循环，使得dp[i][j]和所要查找的最大值能够一起更新，时间复杂度为 $O(n^2)$

代码：

#include<cstdio>
#include<algorithm>
using namespace std;
int n,ans;
int a[3005],b[3005];
int dp[3005][3005];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	for(int i=1;i<=n;i++){
		scanf("%d",&b[i]);
	}
	for(int i=1;i<=n;i++){
		int maxn=0;			//maxn 即前文所提的 sum
		for(int j=1;j<=n;j++){
			dp[i][j]=dp[i-1][j];
			if(a[i]==b[j]){			//满足选择 a[i] 的更新条件
				dp[i][j]=max(dp[i][j],maxn+1);
			}
			if(a[i]>b[j]){			//满足更新最大值的条件
				maxn=max(maxn,dp[i-1][j]+1);
			}
		}
	}
	for(int i=1;i<=n;i++){
		ans=max(ans,dp[n][i]);
	}
	printf("%d",ans);
	return 0;
}

3.2. 输出 LCIS

最近在整理U盘时发现了这个远古代码，应该是很久很久以前 GM 发的

基本思路与输出 LIS，LCS 一样，存储前缀就行

#include<cstdio>
#include<algorithm>
using namespace std;
int n,m,ans,ans_i;
int a[3005],b[3005];
int dp[3005][3005];
int pre[3005];			//pre[i] 表示必选 b[i] 时的 LCIS 的 b[i] 字符的前缀
void print(int num){
	if(!num){			//到头了
		return ;			//跳出即可
	}
	print(pre[num]);			//常规的前缀输出
	printf("%d ",b[num]);
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	scanf("%d",&m);
	for(int i=1;i<=m;i++){
		scanf("%d",&b[i]);
	}
	for(int i=1;i<=n;i++){
		int maxn=1,maxn_i=0;			//maxn 即前文所提的 sum，maxn_i 用于存储前缀下标
		for(int j=1;j<=m;j++){
			dp[i][j]=dp[i-1][j];
			if(a[i]==b[j]){			//满足选择 a[i] 的更新条件
				if(dp[i][j]<maxn){
					dp[i][j]=maxn;
					pre[j]=maxn_i;
				}
			}
			if(a[i]>b[j]){			//满足更新最大值的条件
				if(maxn<dp[i-1][j]+1){
					maxn=dp[i-1][j]+1,maxn_i=j;
				}
			}
		}
	}
	for(int i=1;i<=m;i++){
		if(ans<dp[n][i]){
			ans=dp[n][i],ans_i=i;
		}
	}
	printf("%d\n",ans);
	print(ans_i);			//前缀输出下标
	return 0;
}