【单调队列】笔记

2. 单调队列

单调队列是一个重要的知识点，不仅可以用于DP的优化，还是斜率优化的基础知识（斜率优化有多恶心我就不说了吧）

首先，让我们来了解一下，什么是单调队列

2.1. 单调队列简介

队列，大家都知道是什么，是一种先进先出的数据结构

那么，单调队列是什么呢？

单调队列，在队列的基础上，还保证了队列中元素的单调性

举个例子：

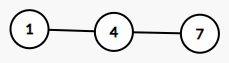
这就是一个单调队列

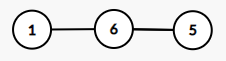
这不是一个单调队列

单调队列的元素删除和普通队列的元素删除是一样的，但是，单调队列的元素插入和普通队列的元素插入可就不一样了

2.1.1. 单调队列的元素插入

我们先用文字来描述一下单调队列的元素插入：

假设我们要插入元素 $s$，判断：如果插入元素 $s$ 后队列不满足单调性，则弹出队尾的元素，然后继续判断；否则，插入元素 $s$

让我们用一些图片来解释一下

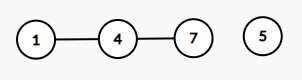
左边是当前的单调队列，右边是我们要插入的元素 $5$

比较：$7>5$，说明此时插入 $5$ 无法满足队列的单调性，则弹出队尾元素 $7$

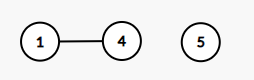
比较：$4<5$，说明此时插入 $5$ 可以满足队列的单调性，插入元素 $5$

关于单调队列本身，其实就已经讲完了

2.1.2. 模板代码

我们用一道水题来引入代码：

Eg_1 滑动窗口 /【模板】单调队列

我们既可以选择用两个单调队列分别维护最小值和最大值，也可以先维护最小值，在将队列初始化后，维护最大值

蒟蒻选择了后者

代码如下：

#include<cstdio>
int n,m;
int a[1000005];
int head=1,tail;
int q[1000005];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	for(int i=1;i<=n;i++){
		while(i-q[head]>=m&&head<=tail){//此时的队首元素下标不在目前的区间范围内，就没有必要再留着了
			head++;
		}
		while(a[q[tail]]>=a[i]&&head<=tail){//维护最小值
			tail--;
		}
		q[++tail]=i;
		if(i>=m){
			printf("%d ",a[q[head]]);
		}
	}
	printf("\n");
	head=1,tail=0;//初始化
	for(int i=1;i<=n;i++){
		while(i-q[head]>=m&&head<=tail){
			head++;
		}
		while(a[q[tail]]<=a[i]&&head<=tail){//维护最大值
			tail--;
		}
		q[++tail]=i;
		if(i>=m){
			printf("%d ",a[q[head]]);
		}
	}
	return 0;
}

2.2. 单调队列优化

从上述的模板题中，我们可以发现：单调队列可以极快地求出区间范围内的最小（大）值

在某些DP中，我们就可以使用单调队列来优化

Eg_2 [USACO11OPEN]Mowing the Lawn G

2.2.1. 朴素DP

定义状态：

我们设dp[i][0]为不选择第 $i$ 头奶牛的最大效率值，dp[i][1]为选择第 $i$ 头奶牛的最大效率值

最终答案存储在max(dp[n][0],dp[n][1])中

考虑状态转移方程式

显然，可以得到：

d p [   i   ] [   0   ] = max ⁡ { d p [   i − 1   ] [   0   ] , d p [   i − 1   ] [   1   ] } d p [   i   ] [   1   ] = max ⁡ { d p [   j   ] [   0   ] + ∑ k = j + 1 i E k } ( i − K ≤ j ≤ i ) dp[\ i\ ][\ 0\ ]=\max\{dp[\ i-1\ ][\ 0\ ],dp[\ i-1\ ][\ 1\ ]\}\\dp[\ i\ ][\ 1\ ]=\max\{dp[\ j\ ][\ 0\ ]+\sum\limits_{k=j+1}^{i}E_k\}(i-K\le j\le i) dp[ i ][ 0 ]=max{dp[ i−1 ][ 0 ],dp[ i−1 ][ 1 ]}dp[ i ][ 1 ]=max{dp[ j ][ 0 ]+k=j+1∑i​Ek​}(i−K≤j≤i)

我们设 $pre[i]=\sum _{k=1}^i{E}_k$，则可以进一步化简转移方程式：

d p [   i   ] [   1   ] = max ⁡ { d p [   j   ] [   0   ] + p r e [   i   ] − p r e [   j   ] } dp[\ i\ ][\ 1\ ]=\max\{dp[\ j\ ][\ 0\ ]+pre[\ i\ ]-pre[\ j\ ]\} dp[ i ][ 1 ]=max{dp[ j ][ 0 ]+pre[ i ]−pre[ j ]}

时间复杂度为 $O(n^2)$

2.2.2. 单调队列优化DP

为了让单调队列派上用场，我们要进一步化简状态转移方程式：

d p [   i   ] [   1   ] = p r e [   i   ] + max ⁡ { d p [   j   ] [   0   ] − p r e [   j   ] } dp[\ i\ ][\ 1\ ]=pre[\ i\ ]+\max\{dp[\ j\ ][\ 0\ ]-pre[\ j\ ]\} dp[ i ][ 1 ]=pre[ i ]+max{dp[ j ][ 0 ]−pre[ j ]}

因为 $i-K\le j\le i$，所以，方程式里的后面一坨就相当于求区间 $[i-K,i]$ 内，$dp[j][0]-pre[j]$ 的最大值

这就可以运用单调队列了来优化了

代码如下：

#include<cstdio>
#include<algorithm>
using namespace std;
long long int n,m,head,tail;
long long int q[100005];
long long int a[100005],pre[100005];
long long int dp[100005][2];
int main(){
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%lld",&a[i]);
		pre[i]=pre[i-1]+a[i];
	}
	for(int i=1;i<=n;i++){
		dp[i][0]=max(dp[i-1][0],dp[i-1][1]);//先求dp[i][0]
		while(i-q[head]>m&&head<=tail){//维护队首
			head++;
		}
		dp[i][1]=pre[i]+dp[q[head]][0]-pre[q[head]];//队首即为最优解，用它来求解dp[i][1]
		while(dp[i][0]-pre[i]>dp[q[tail]][0]-pre[q[tail]]&&head<=tail){//维护队尾
			tail--;
		}
		q[++tail]=i;
	}
	printf("%lld",max(dp[n][0],dp[n][1]));
	return 0;
}