解锁棋盘之谜：探索N皇后问题的全方位解决策略【python 力扣51题】

作者介绍：10年大厂数据\经营分析经验，现任大厂数据部门负责人。
会一些的技术：数据分析、算法、SQL、大数据相关、python
欢迎加入社区：码上找工作
作者专栏每日更新：
LeetCode解锁1000题: 打怪升级之旅
python数据分析可视化：企业实战案例
备注说明：方便大家阅读，统一使用python，带必要注释，公众号 数据分析螺丝钉 一起打怪升级

题目描述

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例 1：

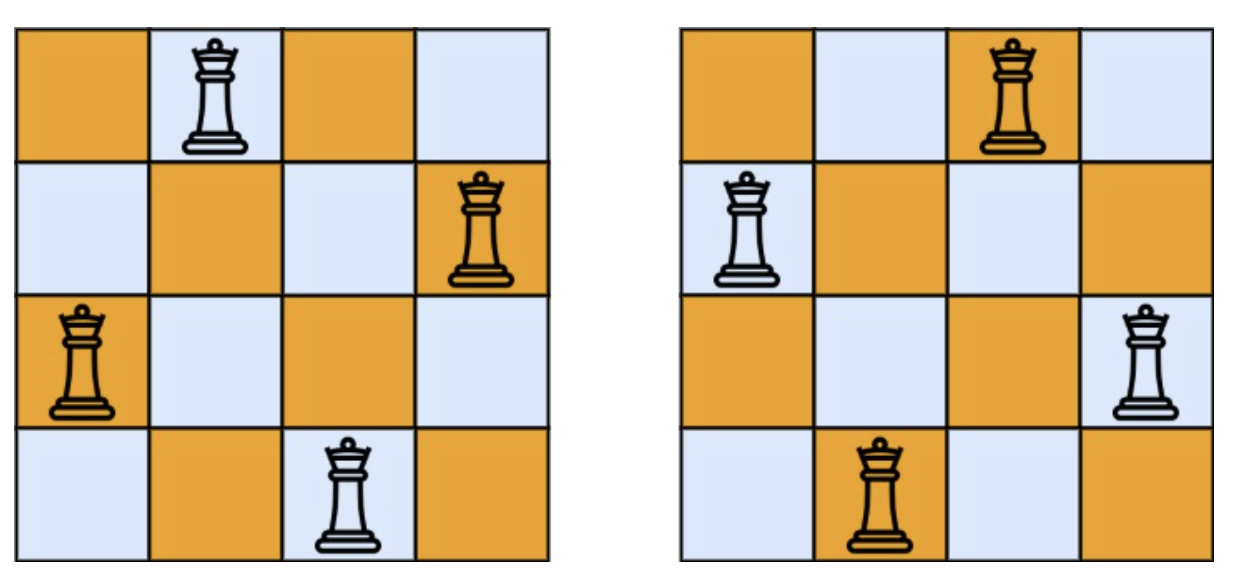
输入格式

• n：一个整数，表示棋盘的大小（即棋盘有 n 行和 n 列）。

输出格式

• 返回所有独特的 n 皇后问题的解决方案。

输入: n = 4
输出: [
 ["..Q.",  // 解法 1
  "Q...",
  "...Q",
  ".Q.."],
 ["Q...",  // 解法 2
  "..Q.",
  "Q...",
  "...Q"]
]

示例 2：

输入：n = 1
输出：[["Q"]]

方法一：回溯算法

解题步骤

1. 初始化：创建一个 n×n 的棋盘，开始时每个位置都是空的 '.'。
2. 回溯函数：使用递归函数 backtrack 来试探每一行的每一个位置，检查放置皇后是否合法。
3. 合法性检查：为每个皇后的位置进行合法性检查，确保没有两个皇后能攻击到对方。
4. 递归与回溯：递归地放置下一个皇后，如果当前放置不合法则回溯（撤销上一步的操作）。

完整的规范代码

def solveNQueens(n):
    def backtrack(row, diagonals, anti_diagonals, cols, state):
        # Base case - a valid solution is found
        if row == n:
            board = build_board(state)
            solutions.append(board)
            return
        
        for col in range(n):
            curr_diagonal = row - col
            curr_anti_diagonal = row + col
            
            # If the queen is not placeable
            if (col in cols or curr_diagonal in diagonals or curr_anti_diagonal in anti_diagonals):
                continue
            
            # "Add" queen to the board
            cols.add(col)
            diagonals.add(curr_diagonal)
            anti_diagonals.add(curr_anti_diagonal)
            state.append(col)
            
            # Move on to the next row with the updated state
            backtrack(row + 1, diagonals, anti_diagonals, cols, state)
            
            # "Remove" queen from the board (backtrack)
            cols.remove(col)
            diagonals.remove(curr_diagonal)
            anti_diagonals.remove(curr_anti_diagonal)
            state.pop()

    def build_board(state):
        board = []
        for i in range(n):
            row = ['.' for _ in range(n)]
            row[state[i]] = 'Q'
            board.append(''.join(row))
        return board

    solutions = []
    backtrack(0, set(), set(), set(), [])
    return solutions

# 示例调用
print(solveNQueens(4))

算法分析

• 时间复杂度：(O(n!))，每层递归减少的选择数大约是 n，因此时间复杂度接近于 n!。
• 空间复杂度：(O(n))，主要消耗在递归栈上。

方法二：位运算优化的回溯算法

解题步骤

1. 利用位运算：使用整数的位来代表棋盘上的列和对角线的占用情况，通过位运算来快速检查和修改状态。
2. 优化回溯：通过位运算加速合法位置的检查过程，使用位掩码来控制递归过程。

完整的规范代码

def solveNQueens(n):
    def backtrack(row, cols, diag1, diag2, state):
        if row == n:
            board = build_board(state)
            solutions.append(board)
            return
        
        available_positions = (~(

cols | diag1 | diag2)) & ((1 << n) - 1)
        
        while available_positions:
            position = available_positions & -available_positions
            col = bin(position).count('0') - 1
            state.append(col)
            backtrack(row + 1, cols | position, (diag1 | position) << 1, (diag2 | position) >> 1, state)
            state.pop()
            available_positions &= available_positions - 1

    def build_board(state):
        board = []
        for i in range(n):
            row = ['.' for _ in range(n)]
            row[state[i]] = 'Q'
            board.append(''.join(row))
        return board

    solutions = []
    backtrack(0, 0, 0, 0, [])
    return solutions

# 示例调用
print(solveNQueens(4))

算法分析

• 时间复杂度：(O(n!))，尽管实际上比普通的回溯要快，因为位运算提供了更快的速度。
• 空间复杂度：(O(n))，空间消耗主要在递归栈上。

方法三：基于列和对角线的回溯

解题步骤

1. 标记法：使用三个标记数组，分别记录列和两个方向的对角线的占用情况。
2. 简化检查：通过标记数组，简化每次放置皇后时的合法性检查。

完整的规范代码

def solveNQueens(n):
    def backtrack(row):
        if row == n:
            solutions.append(["".join(row) for row in board])
            return
        
        for col in range(n):
            if not (cols[col] or diag1[row + col] or diag2[row - col + n - 1]):
                board[row][col] = 'Q'
                cols[col] = diag1[row + col] = diag2[row - col + n - 1] = True
                backtrack(row + 1)
                board[row][col] = '.'
                cols[col] = diag1[row + col] = diag2[row - col + n - 1] = False

    board = [["."]*n for _ in range(n)]
    cols = [False]*n
    diag1 = [False]*(2*n-1)
    diag2 = [False]*(2*n-1)
    solutions = []
    backtrack(0)
    return solutions

# 示例调用
print(solveNQueens(4))

算法分析

• 时间复杂度：(O(n!))，对于每一行，逐个检查每列是否可以放置皇后。
• 空间复杂度：(O(n))，需要额外空间来存储棋盘状态及递归栈。

方法四：DFS优化标记

解题步骤

1. 深度优先搜索：使用深度优先搜索遍历所有可能的棋盘配置。
2. 优化标记：使用一维数组存储棋盘状态，通过索引和值的关系减少空间复杂度。

完整的规范代码

def solveNQueens(n):
    def dfs(queens, xy_diff, xy_sum):
        p = len(queens)
        if p==n:
            result.append(queens)
            return None
        for q in range(n):
            if q not in queens and p-q not in xy_diff and p+q not in xy_sum: 
                dfs(queens+[q], xy_diff+[p-q], xy_sum+[p+q])
    result = []
    dfs([], [], [])
    return [ ["."*i + "Q" + "."*(n-i-1) for i in sol] for sol in result]

# 示例调用
print(solveNQueens(4))

算法分析

• 时间复杂度：(O(n!))，尽管通过优化减少了不必要的检查。
• 空间复杂度：(O(n))，递归深度决定了空间复杂度。

方法五：迭代回溯

解题步骤

1. 迭代回溯：使用栈来模拟递归过程，避免函数调用的开销。
2. 状态管理：显式地在迭代中管理棋盘状态和递归变量。

完整的规范代码

def solveNQueens(n):
    stack = [(0, [], [], [])]  # (row, queens, xy_diff, xy_sum)
    results = []
    while stack:
        row, queens, xy_diff, xy_sum = stack.pop()
        if row == n:
            board = build_board(queens)
            results.append(board)
        else:
            for col in range(n):
                if col not in queens and row - col not in xy_diff and row + col not in xy_sum:
                    stack.append((row + 1, queens + [col], xy_diff + [row - col], xy_sum + [row + col]))
    
    return results

def build_board(queens):
    n = len(queens)
    board = []
    for i in queens:
        board.append('.' * i + 'Q' + '.' * (n - i - 1))
    return board

# 示例调用
print(solveNQueens(4))

算法分析

• 时间复杂度：(O(n!))，尽管迭代可能减少了一些函数调用开销。
• 空间复杂度：(O(n))，主要由栈的深度决定。

不同算法的优劣势对比

特征	方法一: 回溯算法	方法二: 位运算优化回溯	方法三: 基于标记的回溯	方法四: DFS优化标记	方法五: 迭代回溯
时间复杂度	(O(n!))	(O(n!))	(O(n!))	(O(n!))	(O(n!))
空间复杂度	(O(n))	(O(n))	(O(n))	(O(n))	(O(n))
优势	- 易于理解和实现	- 空间效率高	- 易于调试和实现	- 空间利用最优化	- 避免递归，减少调用开销
劣势	- 空间消耗较大	- 理解和实现复杂	- 状态管理较为复杂	- 实现较为复杂	- 状态维护复杂

应用示例

算法竞赛和面试：
在算法竞赛和技术面试中，N皇后问题是一类常见的问题，用于测试候选人的递归思维和问题解决能力。掌握多种解决方法可以在不同的面试环境中灵活应对。

教育和研究：
N皇后问题在算法教学和计算机科学研究中有广泛应用，常作为回溯算法和递归思想的示例问题。通过这个问题，可以深入理解递归、回溯以及剪枝等概念。

这些算法及其对比提供了一个全面的视角来理解和应用不同的编程技巧和优化方法，适用于解决实际问题并优化现有解决方案。