【算法】单源最短路——Dijkstra

对于固定起点的最短路算法，我们称之为单源最短路算法。单源最短路算法很多，最常见的就是dijkstra算法。

dijkstra主要用的是一种贪心的思想，就是说如果i...s...t...j是最短路，那么i和j之间的任意两点s,t之间也一定是最短路，非常好证，如果s，t之间不是最短路，那么必然存在最短路，那么i到j也不是最短路造成了矛盾。

而dijkstra就是运用这样的思想，把起点首先放进一个集合S中，其他的点在另一个集合中，每次取起点经过集合S中的点可达的最短路的点，加入到集合S中，并且根据新加入的店刷新一遍最短路。直到所有的点都在集合S中。

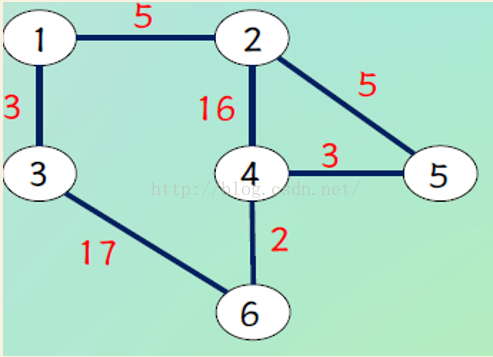
如上图，假设以1为起点，dis[i]为起点到i点的最短距离，如果没法直达则为INF

第一次：S中只有1，那么1能直达的点有2，3，取路径最短的3加入S，并更新一遍dis，发现6可达，dis[6] = 20；

第二次：S中有1，3，可达的有2，6，取2，则4，5可达，dis[4] = 21,dis[5] = 10；

第三次：S中有1，2，3，可达的有4，5，6，取5，到4多了新路径且比原来近，更新dis[4] = 13；

第四次：S中有1，2，3，5，可达的有4，6，取4，到6多了新路径且比原来近，更新dis[6] = 15；

第五次：S中有1，2，3，4，5，可达的有6，只有6不在S中，取6，不更新，完成算法

要注意的是外围循环是除了起点外的点数，如果多一次，pos会无法赋值因为所有的点都遍历过了，造成变量没有初始化而程序崩溃。

代码如下：

#include <