《组合数学》第五版学习笔记（第一、二章）

第一章 什么是组合数学

1.1 例子：棋盘的完美覆盖

有如下结论：
$m\times n$棋盘有$b$格牌的完美覆盖当且仅当$b$或者是$m$的一个因子或者是$n$的一个因子。

如果完美覆盖中所有$b$格牌都是水平放置或者所有$b$格牌都是垂直放置，则称这样的完美$b$格牌覆盖是平凡的。于是$m\times n$棋盘有$b$格覆盖的完美覆盖当且仅当它有平凡完美覆盖。

1.2 例子：幻方

幻方的每一行和每一列以及两条对角线上的数字总和相等，都等于某个整数$s$，称为这个幻方的幻和。

$n$阶幻方中所有整数的和是
$$1+2+3+\cdots +n^2=\frac{n^2(n^2+1)}{2}$$
任意两个$n$阶幻方都有相同的幻和，即
$$s=\frac{n(n^2+1)}{2}$$

构造幻方的 $\text{la Loubeˋre}$方法，其中$n$是奇数。首先把$1$放置在第一行的中间，其后面的整数（从$2$开始）按照它们的自然顺序放置在从左下方到右上方的一条对角线上，并做如下修正：

（1） 当到达第一行时，下一个整数所处的行是最后一行，所处的列是紧跟着前一个整数所处列的后面一列。
（2） 当到达最右边的一列时，下一个整数所处的列是最左边的列（即第一列），它所处的行是紧跟着前一个整数所处行的上一行。
（3） 当达到一个已经填上数字的方格或者已经到达幻方的右上角时，下一个整数放置在上一个数的正下方。

人们研究了三维幻方。$n$阶幻方体$\text{(magic cube)}$是按下述方式由整数$1,2,3,\cdots ,n^3$组成的$n\times n\times n$的立方矩阵，即它在下列线上的$n$个单元中的整数之和$s$都相同：

（1） 与这个立方体的边平行的直线；
（2） 每个平面截面的两条对角线；
（3） 四条空间对角线。

$s$被称为这个幻方体的幻和$\text{(magic sum)}$，它的值等于$(n^4+n)/2$。

不存在三阶和四阶幻方体。

1.3 例子：四色问题

1.4 例子：36军官问题

该问题等价于：能否把$36$个有序对$(i,j)(i=1,2,\cdots ,6;j=1,2,\cdots ,6)$排列成一个$6\times 6$的矩阵，使得在每一行和每一列上整数$1,2,\cdots ,6$都能以某种顺序出现在有序对的第一个位置上，且都能以某种顺序出现在有序对的第二个位置上。

我们可以把这样的矩阵分割成两个$6\times 6$矩阵，其中一个对应于有序对的第一个位置（军衔矩阵），另一个对应于有序对的第二个位置（军团矩阵）。因此，这个问题又可以陈述如下：
是否存在两个$6\times 6$矩阵，它们的项都取自于整数$1,2,\cdots ,6$，使得
（1） 在这两个矩阵中的每一行和每一列上整数$1,2,\cdots ,6$都以某种顺序出现，而且
（2） 当并置这两个矩阵时，所有有序对$(i,j)(i=1,2,\cdots ,6;j=1,2,\cdots ,6)$全部出现？

对于$n$为奇数及含有因子$4$的情况，欧拉给出了如何构造$n$阶正交拉丁方对的方法。1901年，$\text{Tarry}$用穷举法证明了不存在$6$阶拉丁方对。1960年前后，三位数学统计学家$\text{R.C.Bose、E.T.Parker}$和$\text{S.S.Shrinkhande}$成功证明了形如$4k+2,k=2,3,4,\cdots$的每一个$n$，都存在$n$阶正交拉丁方对。

1.5 例子：最短路径问题

1.6 例子：相互重叠的圆

考虑平面上以普通位置相互重叠的$n$个圆${\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_n$。相互重叠指的是每一对圆相交于两个不同点（不允许不想交和相切的圆），普通位置指的是不存在只有一个共同点的三个圆。这$n$个圆在平面内构建若干区域，我们的问题是确定如此构建的区域的数量。

设$h_n$等于构建的区域数。容易计算出$h_1=2$（圆${\gamma }_1$的里面和外面两个区域），$h_2=4$，$h_3=8$.

我们假设$n⩾2$而且在平面上已经画出普通位置下互相重叠的圆
${\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_{n-1}$，它们构建了$h_{n-1}$个区域。然后加入第$n$个圆${\gamma }_n$。使得在普通位置下有$n$个相互重叠的圆。前$n-1$个圆中的每个圆都与第$n$个圆相交出两个点，因为这些点都处于普通位置上，所以我们得到$2(n-1)$个不同点$P_1,P_2,\cdots P_{2(n-1)}$。这$2(n-1)$个点把圆${\gamma }_n$分割成$2(n-1)$条弧，每条弧都创建出一个新区域，给出额外$2(n-1)$个区域。因此，$h_n$满足下面的递推关系：
$$h_n=h_{n-1}+2(n-1)(n⩾2)$$

利用上述递推关系可得$h_n$的通项公式：
$$h_n=n^2-n+2$$

1.7 例子：Nim 游戏

1.8 习题

2.如上图所示，以被切割的白块为中心，可按上图将棋盘分成$4$个部分，由于四个角全部是白块，所以每个部分都恰有一条偶边，由1.1中的结论可知每个部分都可以被多米诺骨牌完美覆盖，所以被切去一个白块后的棋盘可被多米诺骨牌完美覆盖。

3.从染色的角度考虑。用黑白两种颜色为这些囚室交替染色，参考国际象棋棋盘，若左上角为黑色，则右下角也为黑色。设囚犯从左上角出发，因为该囚犯每走一步都会步入一个与先前异色的囚室，所以偶数步之后囚犯应该仍位于黑色的囚室，奇数步之后应该位于白色的囚室，如果要遍历其余63个囚室需要走63步，此时该囚犯所在的囚室应该是白色的，因此63步之后囚犯不可能恰好进入右下角的黑色囚室。

4.$f(1)=1,f(2)=2,f(3)=3,f(4)=5,f(5)=8$是个兔子数列，满足$f(n+2)=f(n+1)+f(n)$，$f(12)=233$.
$g(n)$我还没找出规律来，我写了一个计算$g(n)$的dfs，还能给出每种方法骨牌的摆放方式，有兴趣的点击这里

5.$11$个。

6.必要性：用反证法，如果$n$是奇数，那么总的小立方体个数$n^3$也是奇数，故不可能用三维多米诺骨牌构造出来。充分性显然，每一层都用二维的完美覆盖就可以了。有可能，可类比第二题。

13.关于构造偶数阶幻方，我贴一个链接：https://blog.csdn.net/html5gz/article/details/4804170
需要代码的可以看我另一篇博客
https://blog.csdn.net/CLOCK_112358/article/details/86656703

15.不能，理由如下：$4$阶幻方的幻和为$34$。所以第一行待填的两个数之和是$29$，只能是$16+13$或$15+14$，第一列待填的两个数之和是$28$，只能是$16+12$或$15+13$，因为数字不能重复使用，因此第一行填入的数只能是$15$和$14$，第一列填入的数只能是$16$和$12$:
$$\left[\begin{array}{cccc}2& 3& 15& 14\\ 4& & & \\ 16& & & \\ 12& & & \end{array}\right]\left[\begin{array}{cccc}2& 3& 14& 15\\ 4& & & \\ 16& & & \\ 12& & & \end{array}\right]\left[\begin{array}{cccc}2& 3& 15& 14\\ 4& & & \\ 12& & & \\ 16& & & \end{array}\right]\left[\begin{array}{cccc}2& 3& 14& 15\\ 4& & & \\ 12& & & \\ 16& & & \end{array}\right]$$而副对角线上四个数之和也为$34$，容易验证上面的后两种情况是不可能的。对于前两种情况，容易验证$1$一定在副对角线上：
$$\left[\begin{array}{cccc}2& 3& 15& 14\\ 4& ?& 1& ?\\ 16& 7& & \\ 12& & & \end{array}\right]\left[\begin{array}{cccc}2& 3& 15& 14\\ 4& ?& 7& \\ 16& 1& & \\ 12& ?& & \end{array}\right]\left[\begin{array}{cccc}2& 3& 14& 15\\ 4& ?& 1& ?\\ 16& 6& & \\ 12& & & \end{array}\right]\left[\begin{array}{cccc}2& 3& 14& 15\\ 4& ?& 6& \\ 16& 1& & \\ 12& ?& & \end{array}\right]$$不论这个$1$是与$4$同行还是与$3$同列，该行或者改列都无法再填入未使用过的数字，使得该行或者该列的数字之和为$34$.

17.对于$4k-3$和$4k(k=1,2,\cdots ,m)$行而言，遭到替换的元素的列数为$4i-3$和$4i(i=1,2,\cdots ,m)$，而对于$4k-2$和$4k-1(k=1,2,\cdots ,m)$行而言，遭到替换的元素的列数为$4i-2$和$4i-1$；对于$4k-3$和$4k(k=1,2,\cdots ,m)$列而言，遭到替换的元素的行数为$4i-3$和$4i(i=1,2,\cdots ,m)$，而对于$4k-2$和$4k-1(k=1,2,\cdots ,m)$列而言，遭到替换的元素的行数为$4i-2$和$4i-1$.

设$R_{4k},R_{4k-1},R_{4k-2},R_{4k-3}$分别表示$4k,4k-1,4k-2,4k-3$行经过替换后行中各元素的和（$k=1,2,\cdots ,m$），$C_{4k},C_{4k-1},C_{4k-2},C_{4k-3}$分别表示$4k,4k-1,4k-2,4k-3$列经过替换后列中各元素的和（$k=1,2,\cdots ,m$）则：
$$\begin{array}{rl}{R}_{4k}& =\sum _{i=1}^n(n\cdot (4k-1)+i)+\sum _{i=1}^m(n^2+1-2\cdot (n\cdot (4k-1)+4i-3\left)\right)\\ & +\sum _{i=1}^m(n^2+1-2\cdot (n\cdot (4k-1)+4i\left)\right)\\ & =n^2(4k-1)+\frac{n(n+1)}{2}+m(n^2+1)-2mn(4k-1)-2m(2m-1)\\ & +m(n^2+1)-2mn(4k-1)-2m(2m+2)\\ & =2m(n^2+1)=\frac{n(n^2+1)}{2}\end{array}$$同理可证$R_{4k-1}=R_{4k-2}=R_{4k-3}=n(n^2+1)/2=C_{4k}=C_{4k-1}=C_{4k-2}=C_{4k-3}$为幻和。对于两条对角线而言，由于它们在替换之前各元素的和就已经等于幻和$n(n^2+1)/2$，而题目所述的替换是具有中心对称性的，即对角线上的替换是该条对角线内部的替换，替换后其各元素的和保持不变，仍为幻和，因此这种构造方法产生的是幻方。

38.设所有$n$条线段长度之和为$s$，因为配对方法只有有限个，故必定存在使$s$最小的配对$p$。假设$p$中有两条线段相交，如下图：

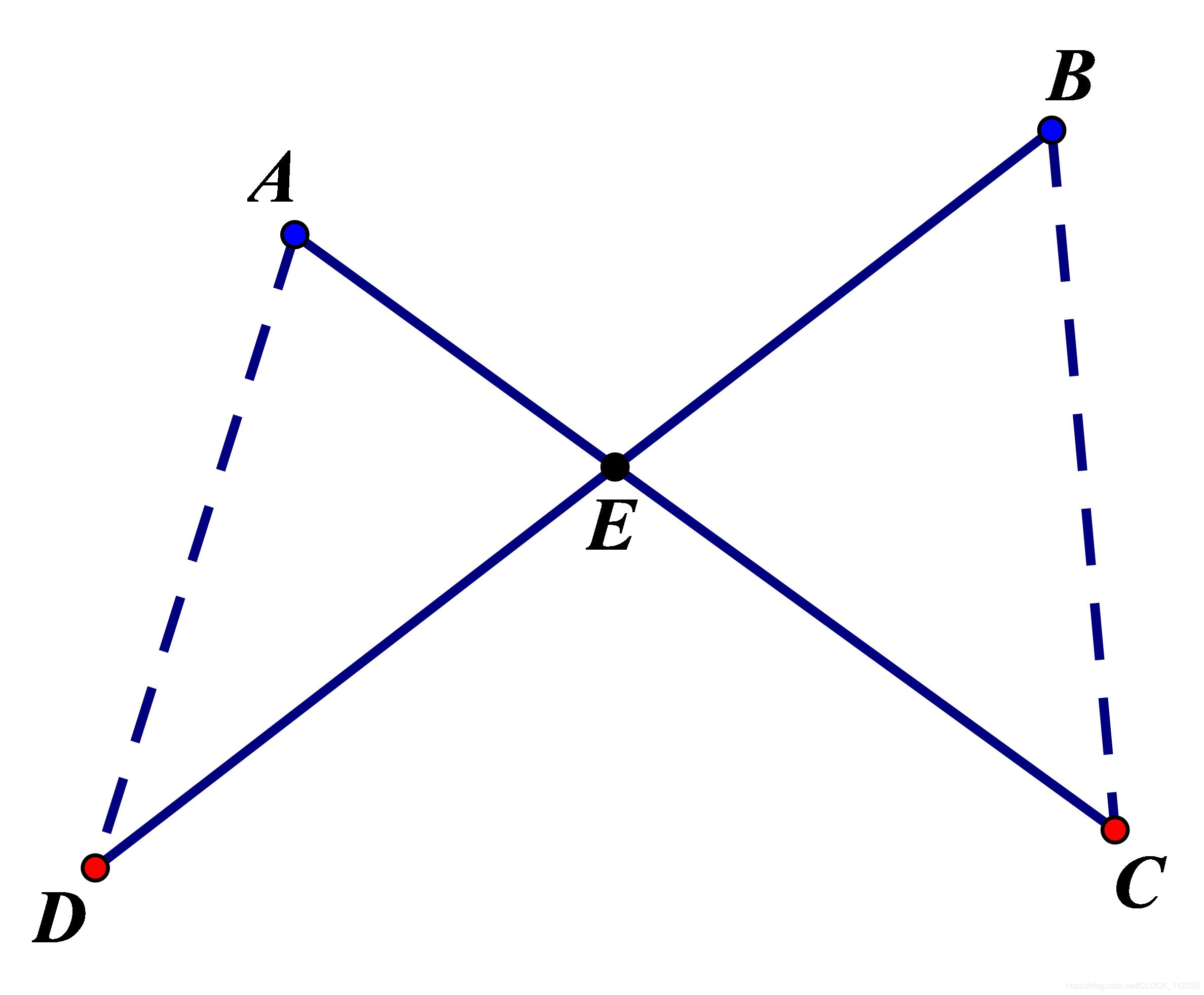
设线段AC与BD相交于点E，将这四个点重新配对并连接，得到线段AD与BC（图中虚线），因为三角形中任意两边之和大于第三边，所以$AD+BC<(AE+ED)+(BE+EC)=AC+BD$，这与$s$最小矛盾，故$p$中不存在两条相交的线段。

39.$n$必须是偶数。给这些方块着色成黑色和白色，位于$1,3,\cdots ,n-1$列的所有方格着黑色，位于$2,4,\cdots ,n$列的方格着白色，黑格数等于白格数。这张棋盘上的L型拼图有两种类型：一种可以覆盖三个黑格和一个白格，一种可以覆盖三个白格和一个黑格。如果$n\equiv 2(\text{mod}4)$，则L型拼图的总个数为奇数，从而上述两种类型的拼图数量不可能相同，这将导致黑格和白格的数目不同，产生矛盾。

42.用黑白交替给棋盘染色，总有一种颜色的格子比另一种颜色格子多。

43.不可能。中心的那块小立方体的六个面必须是人为切出来的，但是一刀不能拐弯切，所以最少切六刀。

第二章 排列与组合

2.1 四个基本的计数原理

加法原理 设集合$S$被划分成两两不相交的部分$S_1,S_2,\cdots ,S_m$。则$S$的对象数目可以通过确定它的每一部分的对象数目并如此相加而得到：
$$|S|=|S_1|+|S_2|+\cdots +|S_m|$$

乘法原理 令$S$是对象的有序对$(a,b)$的集合，其中第一个对象$a$来自大小为$p$的一个集合，而对于对象$a$的每个选择，对象$b$有$q$种选择。于是，$S$的大小为$p\times q$:
$$|S|=p\times q$$

减法原理 令$A$是一个集合，而$U$是包含$A$的更大集合。设
A ˉ = U \ A = { x ∈ U : x ∉ A } \bar{A} = U \backslash A = \{x\in U:x\notin A\} Aˉ=U\A={x∈U:x∈/​A}是$A$在$U$中的补$\text{(complement)}$。那么$A$中的对象数目$|A|$由下列法则给出：
$$|A|=|U|-|\bar{A}|$$

除法原理 令$S$是一个有限集合，把它划分为$k$个部分使得每一部分包含的对象数目相同。于是，此划分中的部分的数目由下述公式给出：
$$\frac{|S|}{\text{在一个部分中的对象数目}}$$

例 在$0$和$10000$之间有多少个整数恰好有一位数字是$5$?
令$S$为在$0$和$10000$之间恰好有一位数字是$5$的整数的集合。
解法一： 我们对$S$做如下划分：$S_1$是$S$中的一位数的集合，$S_2$是$S$中的两位数的集合，$S_3$是$S$中的三位数的集合，$S_4$是$S$中的四位数的集合，$S$中没有五位数。显然，我们有
$$|S_1|=1$$ $S_2$的数很自然地分成两种类型：（1）个位数字是$5$，（2）十位数字是$5$。第一种类型的数的数目是$8$(十位数字既不能是$0$也不能是$5$)。第二种类型的数的数目为$9$(个位数字不能是$5$)。因此，
$$|S_2|=8+9=17$$用类似的推理我们得到
$$|S_3|=8\times 9+8\times 9+9\times 9=225$$以及
$$|S_4|=8\times 9\times 9+8\times 9\times 9+8\times 9\times 9+9\times 9\times 9=2673$$因此
$$|S|=1+17+225+2673=2916$$

解法二： 通过添加前导零（如$6$看作$0006$，$25$看作$0025$，$352$看作$0352$），可以把$S$中的每一个数都当做$4$位数。现在我们根据数字$5$是位于第$1$位、第$2$位、第$3$位还是第$4$位而把$S$划分成$S_1^{\prime },S_2^{\prime },S_3^{\prime }$和$S_4^{\prime }$。这$4$个集合中每一个都含有$9\times 9\times 9=729$个整数，从而$S$所含整数的数目等于$$4\times 729=2916$$

2.2 集合的排列

我们用$P(n,r)$表示$n$元素集合的$r$排列数目。

定理2.2.1 对于正整数$n$和$r$，$r⩽n$，有
$$P(n,r)=n\times (n-1)\times \cdots \times (n-r+1)=\frac{n!}{(n-r)!}$$

定理2.2.2 $n$元素集合的循环$r$排列的数目是
$$\frac{P(n,r)}{r}=\frac{n!}{r\cdot (n-r)!}$$

2.3 集合的组合（子集）

我们用$\left(\genfrac{}{}{0ex}{}{n}{r}\right)$表示$n$元素集合的$r$子集的数目。

定理2.3.1 对于$0⩽r⩽n$，有
$$P(n,r)=r!\left(\genfrac{}{}{0ex}{}{n}{r}\right)$$因此
$$\left(\genfrac{}{}{0ex}{}{n}{r}\right)=\frac{n!}{r!(n-r)!}$$

推论2.3.2 对于$0⩽r⩽n$，有
$$\left(\genfrac{}{}{0ex}{}{n}{r}\right)=\left(\genfrac{}{}{0ex}{}{n}{n-r}\right)$$

定理2.2.3（帕斯卡公式） 对于所有满足$0⩽k⩽n-1$的整数$n$和$k$，有
$$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\left(\genfrac{}{}{0ex}{}{n-1}{k}\right)+\left(\genfrac{}{}{0ex}{}{n-1}{k-1}\right)$$

定理2.3.4 对于$n⩾0$，有
$$\left(\genfrac{}{}{0ex}{}{n}{0}\right)+\left(\genfrac{}{}{0ex}{}{n}{1}\right)+\left(\genfrac{}{}{0ex}{}{n}{2}\right)+\cdots +\left(\genfrac{}{}{0ex}{}{n}{n}\right)=2^n$$且这个共同值等于$n$元素集合的子集数量。

2.4 多重集合的排列

定理2.4.1 设$S$是有$k$种不同类型对象的多重集合，每一个元素都有无限重复数。那么$S$的$r$排列的数目是$k^r$。

定理2.4.2 设$S$是多重集合，它有$k$种不同类型的对象，且每一种类型的有限重复数分别是$n_1,n_2,\cdots ,n_k$。设$S$的大小为$n=n_1+n_2+\cdots +n_k$。则$S$的排列数目等于
$$\frac{n!}{n_1!n_2!\cdots n_k!}$$

定理2.4.3（含重复元素的全排列，同上，略）

定理2.4.4（没卵用，略）

2.5 多重集合的组合

定理2.5.1 设$S$是有$k$种类型对象的多重集合，每种元素均具有无限的重复数。那么$S$的$r$组合的个数等于
$$\left(\genfrac{}{}{0ex}{}{r+k-1}{r}\right)=\left(\genfrac{}{}{0ex}{}{r+k-1}{k-1}\right)$$

例 设$S$是有$4$种类型对象$a,b,c,d$的多重集合 { 10 ⋅ a , 10 ⋅ b , 10 ⋅ c , 10 ⋅ d } \{10\cdot a,10\cdot b,10\cdot c, 10\cdot d\} {10⋅a,10⋅b,10⋅c,10⋅d}。每一种类型的对象至少出现一次的$S$的$10$组合的个数是多少？
本题答案是下面方程的正整数解的个数：
$$x_1+x_2+x_3+x_4=10$$其中$x_1$代表在$10$组合中$a$的个数，$x_2、x_3、x_4$以此类推。进行变量代换：
$$y_1=x_1-1，y_2=x_2-1，y_3=x_3-1，y_4=x_4-1$$则方程变为
$$y_1+y_2+y_3+y_4=6$$其中$y_i$是非负整数。根据定理2.5.1，新方程非负整数解的个数等于
$$\left(\genfrac{}{}{0ex}{}{6+4-1}{6}\right)=\left(\genfrac{}{}{0ex}{}{9}{6}\right)=84$$

多重集合的下述$r$组合计数问题更加困难：下面的多重集合$S$
S = { n 1 ⋅ a 1 , n 2 ⋅ a 2 , ⋯ &ThinSpace; , n k ⋅ a k } S = \{n_1\cdot a_1,n_2\cdot a_2,\cdots,n_k\cdot a_k\} S={n1​⋅a1​,n2​⋅a2​,⋯,nk​⋅ak​}有$k$种类型的对象，且重复数分别是$n_1,n_2,\cdots ,n_k$。$S$的$r$组合的数量与下面方程的正整数解的个数相同：
$$x_1+x_2+\cdots +x_k=r$$其中
$$0⩽x_1⩽n_1,0⩽x_2⩽n_2,\cdots ,0⩽x_k⩽n_k$$

我们将在第$6$章指出如何利用容斥原理对此情形给出满意的方法。

2.6 有限概率

略

2.7 练习题

5.一个数的素因子分解中每有一对2和5，末尾就有一个“0”，又在这两个数中因子2的个数一定比因子5的个数多，因此这两个数中因子5的个数，就是这两个数末尾的零的个数。因为$25=5^2$，所以从1开始每连续25个数相乘就会有6个因子5，$125=5^3=5\cdot 25$，所以从1开始每连续125个数相乘就有$5\cdot 6+1=31$个因子5，从1开始每连续625个数相乘就有156个因子5，以此类推。所以50！中有$6+6=12$个因子5，即其末尾有12个“0”.而$1000=625+3\cdot 125$，所以1000!中有$156+3\cdot 31=249$个因子5，即末尾有249个“0”。

11.所有的取法有$\left(\genfrac{}{}{0ex}{}{20}{3}\right)$种，其中有且仅有两个数连续的取法有$17\cdot 2+16\cdot 17=306$种，三个数是连续的取法有18种，所以没有两个连续的数的取法有$\left(\genfrac{}{}{0ex}{}{20}{3}\right)-306-18$种。

17.第一问是$6!$，如果是2个红车4个蓝车，就乘上$\frac{6!}{2!4!}$.

32.$\frac{11!}{2!4!5!}+\frac{11!}{3!3!5!}+\frac{11!}{3!4!4!}$.(实际上11排列与12排列可以一一对映，数目是一样的)

37.$\left(\genfrac{}{}{0ex}{}{12+5}{5}\right)$

51.若组合中有$k$个$a$，则相应组合的个数为$\left(\genfrac{}{}{0ex}{}{n}{n-k}\right)$，所以总组合数为${\sum }_{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{n-k}\right)={\sum }_{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)=2^n$.(也可以这样理解：先从集合 { 1 , 2 , ⋯ &ThinSpace; , n } \{1,2,\cdots ,n\} {1,2,⋯,n}中选出一个子集，有$2^n$种选法，其中元素不够$n$个的用$a$补上)。