IEEE754浮点数标准相关

①浮点数值的分类（规格化…）

②如何从小数转换成浮点数

③最小不能精确表示的整数

定点表示法：小数点固定，定点整数中小数点隐含固定在数据最右端，定点小数中小数点隐含固定在数据最左端。这种方法并不能有效地表示数字非常大的数，比如$5\ast 2^{100}$，用定点表示法需要101后面跟随100个0来组成，这显然不够高效方便。

浮点数表示法：类似“科学计数法”的思路，可以表示极大或者极小的数字，小数点不是固定的。IEEE 754浮点标准：32位单精度，64位双精度，128位四精度。
                                                           $V=(-1{)}^S\ast 2^E\ast M$

• 符号S：判断正负。

• 阶码E：是浮点数的加权，类似于“科学计数法”中10右上角的指数，以此来缩小所需的存储空间。

• 尾数M：表示浮点数中的有效位数
  

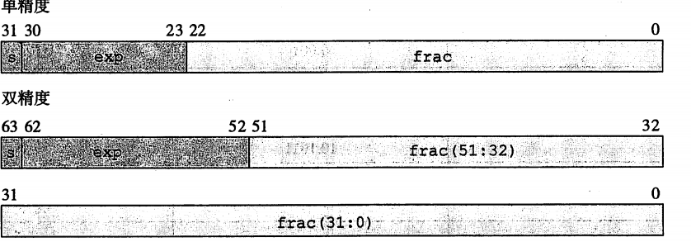
规格化

浮点数的尾数总是规格化的，范围为$1.000\dots 0\ast 2^E$到$1.111\dots \ast 2^E$，规格化下最高位总是1，这使得尾数所有位都是有效的，精度最高。因此存入存储器的时候，f != M，f是去掉1后M的小数部分。而对于阶码E，存在一个叫做偏置值的概念，即E是真正的指数，但8位的阶码位e必须得是大于0的二进制数，这样做的优点是，若E是最小的负指数，阶码位e可以变成00000000来表示，这样0就可以用尾数0和0来表示。单精度下偏置数Bais一般为127，而E=e-Bais。当e在[ 1,127 ) E是负数， [ 127, 254 ]E是正数。之所以偏置数设为127，正是出于平分负数和正数的考虑。

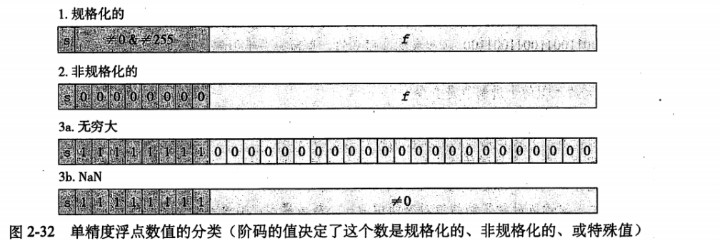
非规格化

当阶码域全为0时，所表示的数就是非规格化形式，这种情况下E=1-Bias。假定8位浮点格式，符号位为1，阶码位为4，尾数位为3，因此偏置码为$2^{4-1}-1=7$，E=1-7=-6。相较于E=-Bais，E=1-Bais从非规格化数到规格化数过渡会更加平滑。

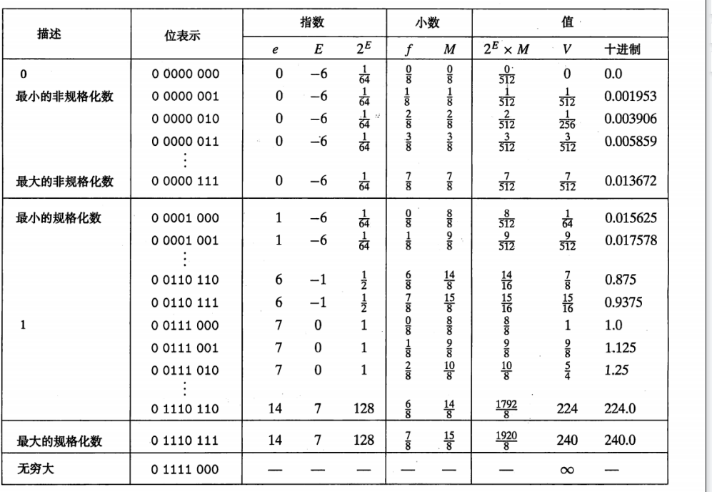
特殊值

1.当阶码位全为1，而小数位全为0时，表示得到的数是无穷大，s=0则为正无穷大，s=1则为负无穷大。单精度下，相当于$(-1{)}^S\ast 1.0\ast 2^{255}$，二进制表示的话已经是上限容量了。

2.当阶码位全为1，但小数位不为0时，我们得到非数（NaN），即IEEE754标准格式不能表示的数。

举个例子：

1.将十进制数4100.125转换成IEEE754下标准的32位单精度二进制浮点数
①十进制转二进制
4100=1000000000100，0.125=0.001
故4100.125=10000000001000.001
②将二进制数规格化
$10000000001000.001=1.0000000001000001\ast 2^{13}$
S=0，M=0000000001000001，e=13+127=140（D）=10001100（B）
因此结果是0 10001100 000000000100000100000000

2.浮点数转十进制同理

舍入
IEEE754标准中规定，缺省的舍入应该往最近的值舍入。如果一个数与两个最近的可表示的值的距离相等，则选择最低位为0的作为舍入值，也就是说，向偶数值舍入。同时提供了其他三种舍入模式。

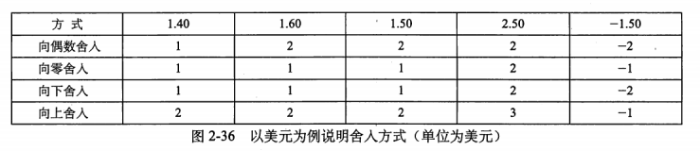
举个例子，例如有效数字超出规定数位的多余数字是1001，它大于超出规定最低位的一半（即0.5），故最低位进1。如果多余数字是0111，它小于最低位的一半，则舍掉多余数字（截断尾数、截尾）即可。对于多余数字是1000、正好是最低位一半的特殊情况，最低位为0则舍掉多余位，最低位为1则进位1、使得最低位仍为0（偶数）。

运算

相乘

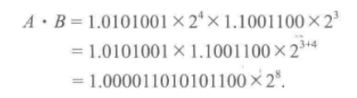
相加（不能直接相加），如下指数不齐的情况，为了对齐指数，需要：

1.找出指数较小的那个数。
2.使两个指数相同。
3.尾数相加或相减。
4.规格化结果。

因此最终结果是$1.00001111\ast 2^5$

最小不能精确表示的整数

表达式$(-1{)}^S\ast 2^E\ast M$，M是一个小数并且它的位数是23，那么它的小数部分最小就是$2^{-23}$。我们可以想象，当E≤23的情况下，每当M的小数位增1的时候，M的小数位都找到唯一一个与之对应的幂次$E^{\prime }$，使得$2^{E^{\prime }}\ast 2^E=1$。也就是说此时每当M加1，都是可以进行精确表示的。

当E＞23的时候，不妨取E=24，就算是M的最低位增1，那么也是$2^{-23}\ast 2^{24}=2$，即增加的是2，也就是中间的从该数增1的整数不能正确表示。

综上所述，我们可以知道不能精确表示的最小正整数是$2^