矢量法证明三面直角棱镜的底面入射光的反射光性能

        三角直面棱镜（立方角锥棱镜），相当于一个立方体切下来的一个角。如图一。

              

                                        图一

       其重要特性之一，是从底面以任意方向入射于棱镜的光线，经过三个面的顺序反射以后，出射光线以与入射光线平行的方向射出，即出射光线相对于入射光线旋转180°。本文采用矢量的方法，加以分析证明。同时，采用GNU OCTAVE绘图，辅助分析。

       将三角直面棱镜设置为一个直角坐标系下顶点为（0 0 0，1 0 0 ，0 1 0，0 0 1）的锥体，如图二所示。

                       

                                            图二

      假设三角直面棱镜OABC是一个折射率为n的实心物体， 任意一束光线由ABC面射入时，由空气进入，会形成折射。这里暂时不考虑折射的情况，即，只考虑光线进入锥体后的情况。因为如果两束光线平行，无论在折射前或折射后，都是平行的。

     设有一点R(x0,y0,z0),经过该点的光线的向量为（a,b,c）,则这条光线可以表示为：

     x=x0+a*t;

     y=y0+b*t;

     z=z0+c*t;

例子中，R(x0,y0,z0)=(0.5,1,1.5)，向量（a,b,c）=(-1,-3,-3)。如图三。

  

                                       图三

         设这条光线与OAC面（即，y=0）交于一点p(xp,yp,zp)。

        由于yp=y0+bt=0,所以，t=-y0/b,

        得到p点坐标为：

         xp=x0-a/b*y0;

         yp=0;

         zp=z0-c/b*y0;

        该光线在遇到OAC面后，进行反射。反射光线在R点在OAC的对称点与p点的直线上。

        R点在OAC面（即，XOZ面）的对称点为R1，可以直接写出关于XOZ面的对称点为R1(x0,-y0,z0)。

        从而，可以得出经过点R1、P的直线为：

          x=xp+t1*(xp-x0);

          y=yp+t1*(yp+y0)=t1*y0;

          z=zp+t1*(zp-z0);

        可以画出图形如图四。

                                       图四

       从而得出该直线与OBC面（即：X=0面）的交点为Q(xq,yq,zq):

          xq=0;

       yq=-y0+b/a*x0;

       zq=z0-c/a*x0;

      R1点关于YOZ平面的对称点为R2,其坐标直接写出为R2（-x0,-y0,z0）。从而，连接Q、R2的直线为：

       x=xq+t2*(xq+x0)=t2*x0;

       y=yq+t2*(yq+y0);

       z=zq+t2*(zq-z0);

      可以画出该直线，如图五。该直线是光线在OBC面的反射线。可以看到，与OAB面（即，z=0）相交。

    图五

        设反射线与Z=0面相交于T(xt,yt,zt),可以求得：

          xt=a/c*z0-x0;

          yt=-y0+b/c*z0;

          zt=0;

        R2点关于XOY平面(z=0)的对称点为R3,其坐标直接写出为R3（-x0,-y0,-z0）。从而，连接点T、R3的向量R3T^(x1,y1,z1)=OT^-OR3^为：

          x1=a/c*z0-x0-(-x0)=a/c*z0;

          y1=-yo+b/c*z0-(-y0)=b/c*z0;

          z1=0-(-z0)=z0;

       如图六。

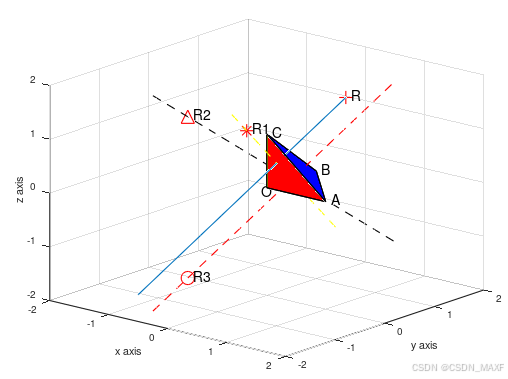
 图六

      从图六看出，点R3、T的连线，如图中的红色线，与入射光（经过R点的直线）是平行的。

判断空间向量是否平行，只需求这两个向量的叉积，如果叉积为0，说明两个向量平行。

     为此，求（a,b,c）X(a/c*z0,b/c*z0,z0)的结果.

     也可以用行列式表示为：

    |  x       y       z   |       | x    y    z  |

    |  a       b       c   |=z0/c* | a    b    c  |=0.

    | a/c*z0   b/c*z0   z0  |       | a    b    c  |

所以，这两个向量是平行的。

而且，从向量（x1,y1,z1）的值，看出与原始向量（a,b,c）的方向关系。

由此，证明出射光线与入射光线平行。

附部分代码：

  

  clear all

close all

a=-1;

b=-3;

c=-3;

x0=0.5;

y0=1;

z0=1.5;

t=0:0.1:2;

x=x0+t.*a;

y=y0+t.*b;

z=z0+t.*c;

plot3(x,y,z);

xlabel('x axis');

ylabel('y axis');

zlabel('z axis');

grid on;

hold on;

vertices=[0 0 0;1 0 0;0 1 0;0 0 1];

fill3(vertices(2,:),vertices(3,:),vertices(4,:),'b');

fill3(vertices(1,:),vertices(3,:),vertices(4,:),'y');

fill3(vertices(2,:),vertices(1,:),vertices(4,:),'r');

fill3(vertices(2,:),vertices(3,:),vertices(1,:),'k');

   END