文章目录
一、基础算法(上)
1 快速排序模板
这个模板的好处是如果应对全部相同的元素3 3 3 3 3 3 3,它一样可以保持每次都能取到接近中点的位置,这样应对这种情况时,时间复杂度可以保持在O(nlogn),而其他写法如果遇到全部相同的元素会因为每次都只能舍掉1个元素而导致会递归n层,使得时间复杂度变为O(n^2)。
void quick_sort(int* q, int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do i++; while (q[i] < x);
do j--; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
}
2 快速选择的两种模板

快速选择算法:
思路:一次快排单趟后,左边区间的数是小于等于右边区间的数的,假设左边区间的元素个数是Sl,右边区间的元素个数是Sr。
如果k <= Sl,那么第k小的数一定在左边区间,递归处理左边区间,找左边区间的第k个数;
如果k > sl,那么第k小的数一定在右半区间,递归处理右边区间,找右半区间的第k - sl个数。
假设每次都均匀二分,时间复杂度计算:
第
一
次
单
趟
长
度
n
第
二
次
单
趟
长
度
n
2
第
三
次
单
趟
长
度
n
4
.
.
.
所
以
总
的
计
算
长
度
为
n
+
n
2
+
n
4
+
.
.
.
=
n
(
1
+
1
2
+
1
4
+
.
.
.
)
<
2
n
所
以
时
间
复
杂
度
为
O
(
n
)
第一次单趟长度n\\ 第二次单趟长度\frac{n}{2}\\ 第三次单趟长度\frac{n}{4}\\ ...\\ 所以总的计算长度为n + \frac{n}{2} + \frac{n}{4}+...=n(1 + \frac{1}{2} + \frac{1}{4} + ...)<2n\\ 所以时间复杂度为O(n)
第一次单趟长度n第二次单趟长度2n第三次单趟长度4n...所以总的计算长度为n+2n+4n+...=n(1+21+41+...)<2n所以时间复杂度为O(n)
如果直接排序,那么时间复杂度是O(nlogn),如果使用快速选择算法,时间复杂度是O(n)
/*快速选择算法*/
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int q[N];
int quick_select(int* q, int l, int r, int k)
{
/*我们会控制答案一直在l到r区间内
所以如果下标相等说明 就是答案了*/
if (l == r) return q[l];
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do i++; while (q[i] < x);
do j--; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
int sl = j - l + 1;/*左区间元素个数*/
/*如果sl大于等于k 说明第k小的数在左区间*/
if (sl >= k) return quick_select(q, l, j, k);
else return quick_select(q, j + 1, r, k - sl);
}
int main()
{
int n, k;
cin >> n >> k;
for (int i = 0; i < n; ++i) cin >> q[i];
cout << quick_select(q, 0, n - 1, k) << endl;
return 0;
}
另一种快速选择模板:

这种要返回最小的k个数或最大的k个数的大概都有三种解法:sort、priority_queue、快速选择,其中快速选择的模板如下:
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k)
{
if (k == 0) return {};
/*借鉴快速选择的思想 当一次快排单趟后
若左边区间的长度等于k 那么左边区间就是最小的k个数
若左边区间的长度小于k 那么第k小的数一定在右半区间
如果左边区间长度大于k 那么第k小的数一定在左半区间*/
quick_select(arr, 0, arr.size() - 1, k);
return {arr.begin(), arr.begin() + k};
}
void quick_select(vector<int>& arr, int l, int r, int k)
{
int i = l - 1, j = r + 1, x = arr[(l + r) >> 1];
while (i < j)
{
do i++; while (arr[i] < x);
do j--; while (arr[j] > x);
if (i < j) swap(arr[i], arr[j]);
}
int sl = j - l + 1;
/*如果k == sl 就不走上面下面直接返回了*/
if (k < sl) quick_select(arr, l, j, k);
else if (k > sl) quick_select(arr, j + 1, r, k - sl);
}
};
3 归并排序模板
const int N = 100010;
int tmp[N];
void merge_sort(int* q, int l, int r)
{
if (l >= r) return;
int mid = (l + r) >> 1;
int i = l, j = mid + 1, k = 0;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
while (i <= mid && j <= r)
{
if (q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
}
while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];
for (i = l, j = 0; i <= r; ++i, ++j)
{
q[i] = tmp[j];
}
}
4 求逆序对的数量

思路:

那么怎么快速统计一半在左半区间一半在右半区间的逆序对个数呢,见下图:
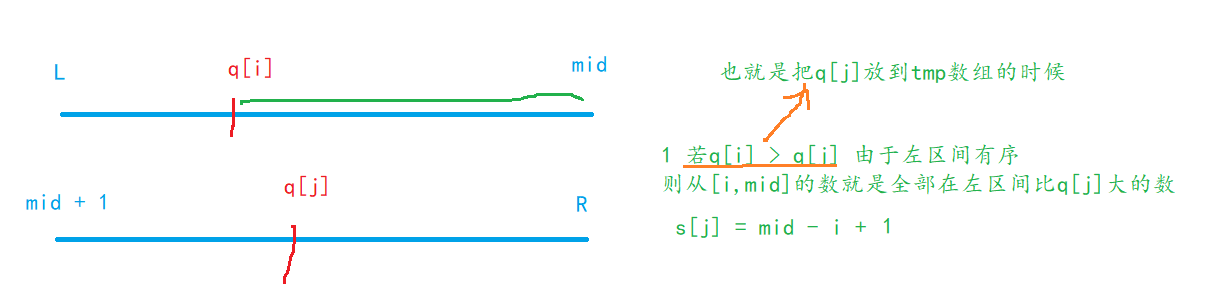
其实假设merge_sort会把该区间的逆序对个数返回,靠得也是分到最底层时下面的归并的过程。
INT_MAX大概是2 * 10^9,超过3 * 1e9就会爆int,本题最大的逆序对数量是全部逆序时,假设数组长度为n,则n - 1 + n - 2 + ... + 1 = n^2 / 2,代入n = 1e5得最大逆序数量为5 * 1e9,会爆int,所以用long long
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int tmp[N];
int q[N];
typedef long long LL;
LL merge_sort(int* q, int l, int r)
{
/*区间不存在或区间只有一个元素 只有0个逆序对*/
if (l >= r) return 0;
int mid = (l + r) >> 1;
//加左区间的逆序对数量和右区间的逆序对数量
LL ret = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);
//归并 同时处理q[i] > q[j]这种左端点在左区间 右端点在右区间的逆序对数量mid - i + j
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r)
{
if (q[i] <= q[j]) tmp[k++] = q[i++];
else
{
/*处理q[i] > q[j]这种左端点在左区间 右端点在右区间的逆序对数量mid - i + j*/
ret += mid - i + 1;
tmp[k++] = q[j++];
}
}
//扫尾
while (i <= mid) tmp[k++] = q[i++];
while (j <= r) tmp[k++] = q[j++];
//归并回去
for (i = l, j = 0; i <= r; ++i, ++j)
{
q[i] = tmp[j];
}
return ret;
}
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; ++i) cin >> q[i];
cout << merge_sort(q, 0, n - 1) << endl;
return 0;
}
5 整数二分
有单调性的题目一定可以二分,但是可以二分的题目不一定有单调性。
本质:可以把区间一分为2,左半边是满足性质1的,右半边是满足性质2的,则二分一定可以找到区间的边界,即找到满足此性质的最右边一个点。
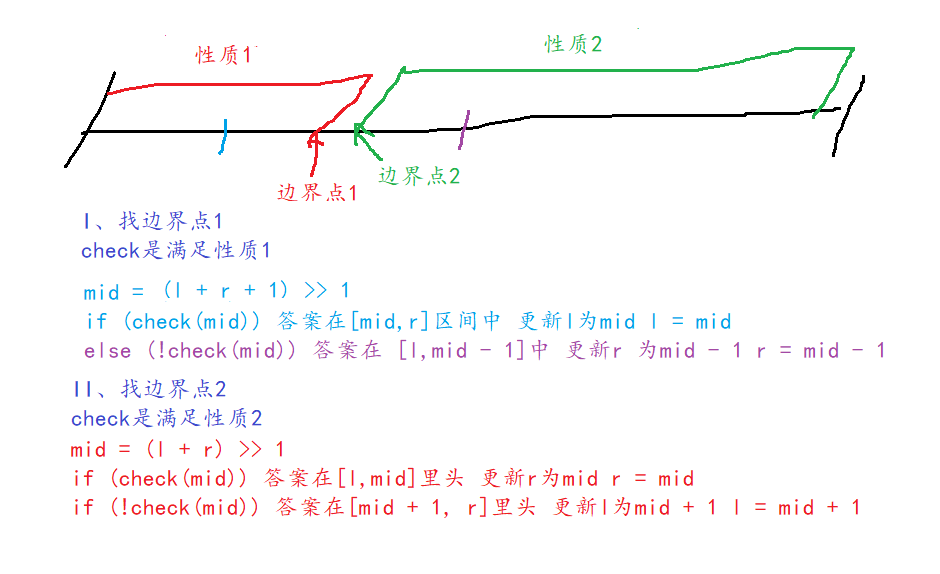
一般选择两种模板的方式是先建模check,然后根据此时区间的更新方式选择是用I还是II,如果更新方式是l = mid,则mid = (l + r + 1) >> 1;,如果更新方式是r = mid,那么mid = (l + r) >> 1;
l = mid更新时+1的原因,如果l = r - 1时,由于C++是向下取整,l + r / 2就等于l,不变,就死循环了。
例题:
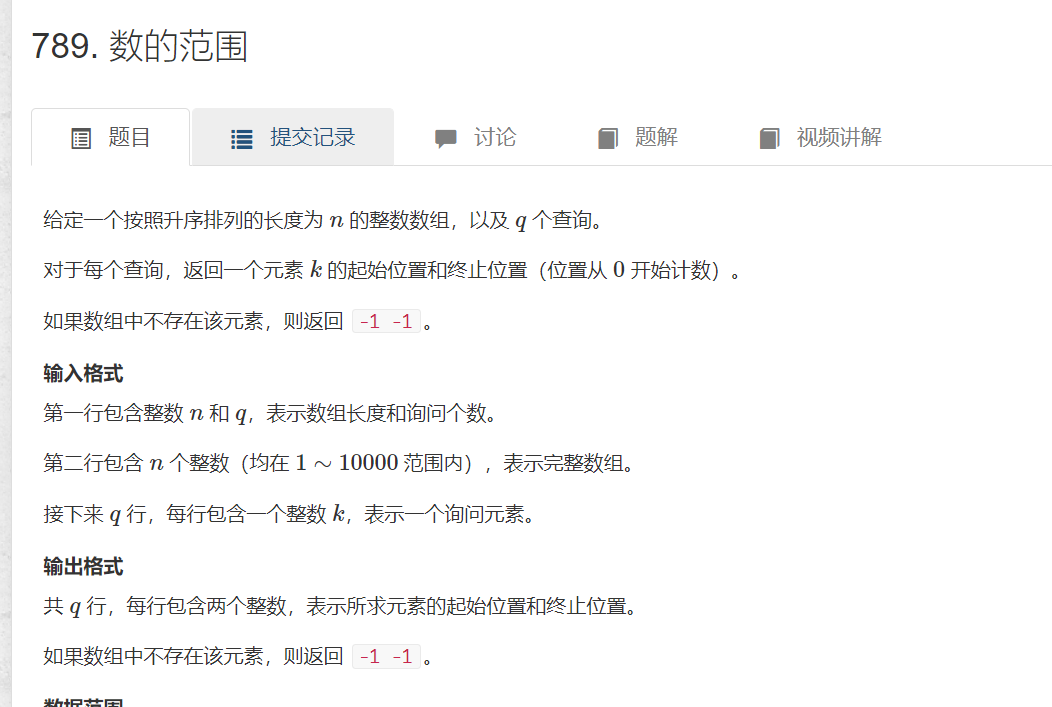
#include <iostream>
using namespace std;
int main()
{
int n, q;
cin >> n >> q;
int a[n];
for (int i = 0; i < n; ++i)
{
cin >> a[i];
}
int x;
while (q--)
{
cin >> x;
/*先找起始位置 定义右边区间全是>=x的 右边区间的左边界点就是起始位置*/
int l = 0, r = n - 1;
while (l < r)
{
int mid = (l + r) >> 1;
if (a[mid] >= x) r = mid;
else l = mid + 1;
}
if (a[l] != x) cout << "-1 -1" << endl;
else
{
cout << l << ' ';
/*再找终止位置 定义左边区间全是<=x的 左边区间的右端点就是终止位置*/
l = 0, r = n - 1;
while (l < r)
{
/*这里更新是 l = mid 所以mid 是(l + r + 1) >> 1*/
int mid = (l + r + 1) >> 1;
if (a[mid] <= x) l = mid;
else r = mid - 1;
}
cout << l << endl;
}
}
return 0;
}
总结:每次都要选择答案所在的区间进行处理,无解的情况是题目可能无界,模板不会无界,因为定义的性质肯定有边界,这个模板一定可以找到这个边界,一般我们都是用二分出的边界来判断题目是否有解。
6 浮点数二分
浮点数二分不存在向下整除的边界问题,所以直接二分就可以了,不用像上面那样处理边界mid = (l + r) / 2 或 mid = (l + r + 1) / 2.
例题:

#include <iostream>
using namespace std;
int main()
{
double x;
cin >> x;
double l = -10000, r = 10000;
while (r - l >= 1e-8)/*这里总比有效位数多2*/
{
double mid = (l + r) / 2;
if (mid * mid * mid >= x)
{
r = mid;
}
else
{
l = mid;
}
}
printf("%.6lf\n", r);
return 0;
}
/*还有一种方法 直接把while改成for循环100次 相当于把区间长度缩小100倍 肯定是够得*/
二、基础算法(中)
1 高精度
I 高精度加法
大整数的位数极端情况下大概有1e6位,大整数加法是两个1e6位的大整数加法。
大整数的储存是存到一个数组里头去,存储数据时,低位存到数组的低位更好一些,这样可以方便的处理进位的问题。
模板
#include <iostream>
#include <vector>
#include <string>
using namespace std;
vector<int> add(const vector<int>& A, const vector<int>& B)
{
int carry = 0;
vector<int> C;
int i = 0, j = 0;
while (i < A.size() || j < B.size() || carry != 0)
{
int tmp = (i == A.size() ? 0 : A[i++]) + (j == B.size() ? 0 : B[j++]) + carry;
C.push_back(tmp % 10);
carry = tmp / 10;
}
return C;
}
int main()
{
string a, b;
cin >> a >> b;
vector<int> A;
vector<int> B;
for (int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
for (int i = b.size() - 1; i >= 0; --i) B.push_back(b[i] - '0');
auto C = add(A, B);
for (int i = C.size() - 1; i >= 0; --i) cout << C[i];
return 0;
}
II 高精度减法
A i − B i − t i f 上 面 小 于 0 , A i + 10 − B i − t 向 下 一 位 借 位 e l s e , A i − B i − t 即 可 A_i - B_i - t\\ if上面小于0,A_i + 10 - B_i - t 向下一位借位\\ else,A_i-B_i-t即可 Ai−Bi−tif上面小于0,Ai+10−Bi−t向下一位借位else,Ai−Bi−t即可
模板
#include <iostream>
#include <string>
#include <vector>
using namespace std;
/*A >= B*/
bool cmp(const vector<int>& A, const vector<int>& B)
{
/*先看看位数是否有差距*/
if (A.size() != B.size()) return A.size() > B.size();
/*从高位往低位比*/
for (int i = A.size() - 1; i >= 0; --i)
{
if (A[i] != B[i]) return A[i] > B[i];
}
return true;/*对应A == B*/
}
vector<int> sub(const vector<int>& A, const vector<int>& B)
{
/*默认A >= B A,B >= 0*/
vector<int> C;
int t = 0;/*定义前一位运算的借位*/
for (int i = 0; i < A.size(); ++i)
{
t = A[i] - (i < B.size() ? B[i] : 0) - t;
C.push_back((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a, b;
cin >> a >> b;
vector<int> A;
vector<int> B;
for (int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
for (int i = b.size() - 1; i >= 0; --i) B.push_back(b[i]- '0');
if (cmp(A, B))
{
auto C = sub(A, B);
for (int i = C.size() - 1; i >= 0; --i) cout << C[i];
}
else
{
auto C = sub(B, A);
cout << '-';
for (int i = C.size() - 1; i >= 0; --i) cout << C[i];
}
return 0;
}
III 高精度乘法
算法思想:高精度A乘短长度的b,把b看成一个整体,结果的每一位都等于(A[i] * b + t) % 10,然后更新进位为t = (A[i] * b + t) / 10
#include <iostream>
#include <string>
#include <vector>
using namespace std;
vector<int> mul(const vector<int>& A, const int b)
{
vector<int> C;
int t = 0;
int i = 0;
while (i < A.size() || t != 0)
{
t = (i < A.size() ? A[i] : 0) * b + t;
C.push_back(t % 10);
t /= 10;
i++;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> A;
for (int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
auto C = mul(A, b);
for (int i = C.size() - 1; i >= 0; --i) cout << C[i];
return 0;
}
IV 高精度除法
本除法是一个高精度整数除以一个低精度整数b,把大整数A从高位往低位排,排成AnAn-1...A0,初始时余数r等于An,每次都求一个余数r整除b的值,商到结果C的back去,然后更新余数为(r % b) * 10 + An-1,循环下去,直到走完A0
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
/*借用引用r返回余数*/
vector<int> div(const vector<int>& A, const int b, int& r)
{
vector<int> C;
for (int i = A.size() - 1; i >=0; --i)
{
r = r * 10 + A[i];
C.push_back(r / b);
r %= b;
}
/*C是先存高位再存低位 为和其它运算一致 需要先逆序*/
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
int r = 0;
vector<int> A;
for (int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
auto C = div(A, b, r);
for (int i = C.size() - 1; i >=0; --i) cout << C[i];
cout << endl << r << endl;
}
2 前缀和
I 一维
假设有一个长度为n的数组:a1 , a2, a3, ..., an,前缀和定义为Si = a1 + a2 + ... + ai.
如何求Si?Si有什么用?
怎么求前缀和? 利用递推公式Si = Si-1 + ai(定义S0 = 0)
作用:快速求出原数组中一段数的和 al + al+1 + ... + ar = Sr - Sl-1,此操作是O(1)的。
为什么下标要从1开始,是为了定义S0,这样方便用统一的公式。
模板:
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N];
int s[N];
int main()
{
int n, m;
int l, r;
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++i)
{
scanf("%d", &a[i]);
s[i] = s[i - 1] + a[i];
}
while (m--)
{
scanf("%d %d",&l, &r);
printf("%d\n", s[r] - s[l - 1]);
}
return 0;
}
II 二维
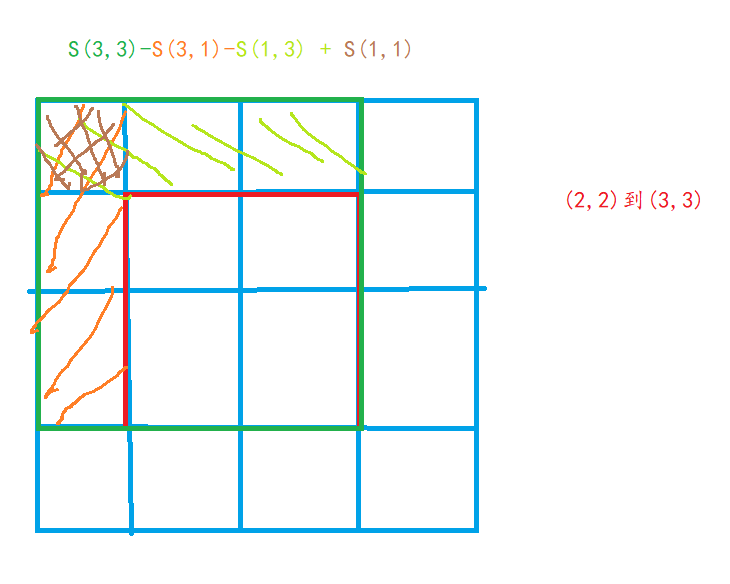
Sij表示以(1,1)到(i,j)组成的长方形内的元素的和。
怎么求?递推公式推导如图:

作用:求(x1, y1)为左上顶点,(x2, y2)为右上顶点的矩形中所有元素的和。
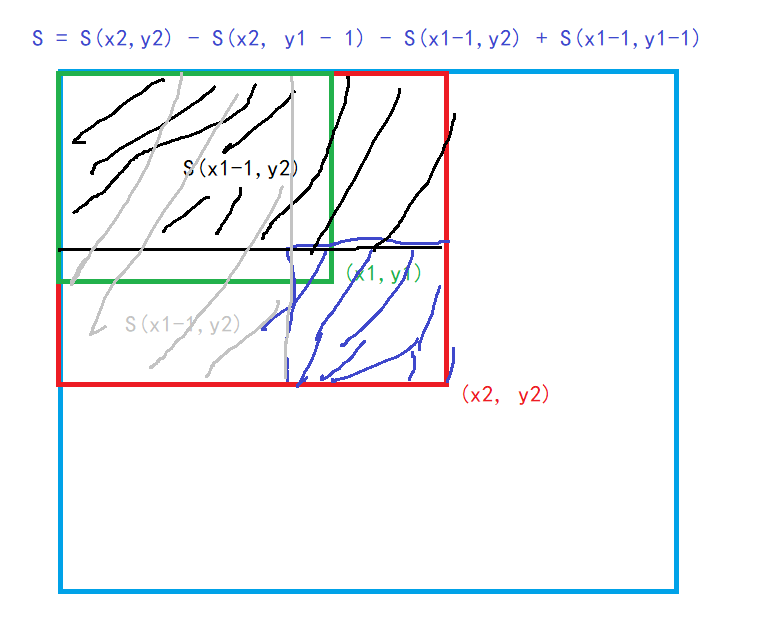
模板代码:
#include <iostream>
using namespace std;
const int N = 1010;
int a[N][N];
int s[N][N];
int main()
{
int n, m , q;
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
scanf("%d", &a[i][j]);
}
}
/*求前缀和矩阵*/
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
s[i][j] = a[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
}
}
/*处理q个询问*/
while (q--)
{
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);
}
return 0;
}
观察边界:
3 差分
I 一维
假设给定数组a1, a2, ..., an,需要构造数组b1, b2, ..., bn使得ai = b1 + b2 +...+ bi,即构造一个b数组使得a数组是b数组的前缀和,则b数组称为a数组的差分。
可以发现前缀和和差分是一对逆运算。
定义b1 = a1,其余情况bi = ai - a(i-1)即可。
差分的作用:
- O(n)的时间由b数组得到a数组。
- 如果有一堆操作,要求给a数组的区间
[l, r]的每个值都加c,如果利用差分,可以让每个操作都是O(1)的,如果要得到增加后了的a数组,则可以用一个O(n)的操作由b数组得到a数组,具体的操作就是bl + c, b(r+1) - c.

差分的构造过程可以视为原始a数组全0,因此差分数组b也是全0,然后对(1,1)区间加a1…对(n,n)区间加an,所以差分不需要构造操作,只需要插入操作就可以了。
模板:
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N];
int b[N];
void Insert(int* gap, int l, int r, int c)
{
gap[l] += c;
gap[r + 1] -= c;
}
int main()
{
int n, m;
int l, r, c;
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i)
{
Insert(b, i, i, a[i]);
}
while (m--)
{
scanf("%d%d%d", &l, &r, &c);
Insert(b, l, r, c);
}
for (int i = 1; i <= n; ++i)
{
a[i] = a[i - 1] + b[i];
}
for (int i = 1; i <= n; ++i)
{
printf("%d ", a[i]);
}
return 0;
}
II 二维
定义一个矩阵A,构造矩阵B使得矩阵A的元素aij是矩阵B(1,1)到(i,j)的前缀和,那么B矩阵就是A矩阵的差分矩阵。
二维差分的主要作用是是给A的某个子矩阵加上值c,这个操作是O(1)的。

所以这里初始化可以这样想:首先假定A矩阵全部值都是0,则B矩阵全部值都是0,然后对A的每个点的赋值可以看做是给每个子矩阵(i,j)-(i,j)插入一个a[i][j],构造差分矩阵的过程可以归类到插入操作中。
#include <iostream>
using namespace std;
const int N = 1010;
int a[N][N];
int b[N][N];
void Insert(int b[N][N], int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y1] -= c;
b[x2 +1][y2 + 1] += c;
}
int main()
{
int n, m , q;
int x1, y1, x2, y2, c;
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
scanf("%d", &a[i][j]);
}
}
/*利用插入初始化差分矩阵b*/
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
Insert(b, i, j, i, j, a[i][j]);
}
}
/*处理q个操作*/
while (q--)
{
cin >> x1 >> y1 >> x2 >> y2 >> c;
Insert(b, x1, y1, x2, y2, c);
}
/*由差分矩阵b求矩阵a*/
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
a[i][j] = b[i][j] + a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
}
}
/*输出*/
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
cout << a[i][j] << ' ';
}
cout << endl;
}
return 0;
}
三、基础算法(下)
1 双指针算法
总共大概两大类:
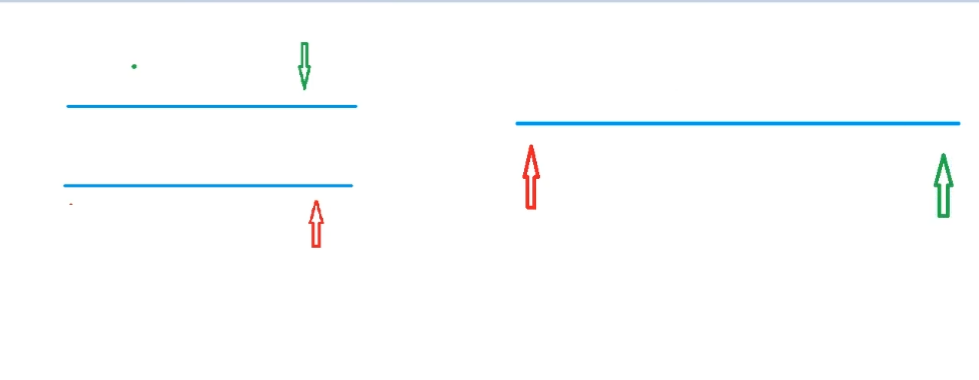
双指针算法的核心思想:把O(n^2)的暴力遍历优化成O(n).
大概模板:
for (int i = 0, j = 0; i < n; ++i)
{
//j合法且满足某种性质则j++
while (j < n && check(i, j)) ++j;
//每个题目的具体逻辑
}
I 最长连续不重复子序列
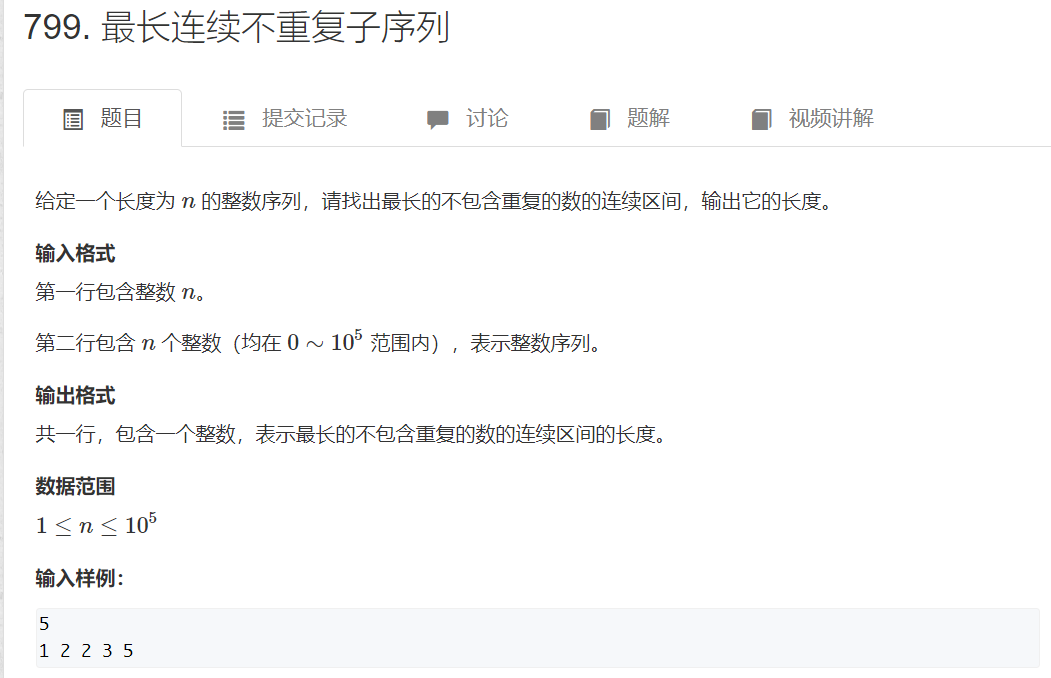
一般这种双指针的题可以先想一下朴素做法,
//枚举终点
for (int j = 0; j < n; ++j)
{
//枚举起点
for (int i = 0; i <= j; ++i)
{
if (check(i, j)) ret = max(ret, j - i + 1);
}
}
其时间复杂度为O(n^2)(不考虑check的复杂度时)
观察到假如定义i为以j结尾的串的最右边端点,会发现当j往后走的时候i一定会往后走或者不动,不可能往前走,因此可以改进如下:
for (int j = 0, i = 0; j < n; ++j)
{
while (i <= j && check(i, j)) ++i;
ret = max(ret, j - i + 1);
}
这样两个指针最多走2n步了,复杂度就优化到O(n)了。
双指针算法的本质就是发现某些性质(尤其是单调性),使得本来我们要枚举n^2个状态转化为枚举O(n)个状态。
具体怎么检查i和j之间维护的是以j结尾的最长不重复子串见下面代码:
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int q[N];
int cnt[N];
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; ++i) cin >> q[i];
/*以i开头 以j结尾的串
其中 i是以j结尾的最长无重复子串的左端点
*/
int ret = 0;
for (int j = 0, i = 0; j < n; ++j)
{
/*先把当前位置的计数弄进来*/
++cnt[q[j]];
/*重复只可能是新进来的q[j]导致重复
因为上一轮都维护的是以j - 1不重复的最长子串*/
while (cnt[q[j]] > 1)
{
/*重复的话就是q[j]的数量不为1
让i往前走把重复的位置走掉*/
--cnt[q[i]];
++i;
}
ret = max(ret, j - i + 1);
}
cout << ret << endl;
}
II 数组元素的目标和

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int A[N];
int B[N];
int main()
{
int n, m, x;
cin >> n >> m >> x;
for (int i = 0; i < n; ++i) cin >> A[i];
for (int i = 0; i < m; ++i) cin >> B[i];
/*
双指针 i指向A的开头 j指向B的结尾
当A[i] + B[j] > x时 j往前退
退到不满足这一条件时
若A[i] + B[j] == x 输出(i,j)
若此时A[i] + B[j] < x 则让i往后移动一位 j不动
这是因为i往前移动一位变为i + 1后
j后面那些位置 根据数组的递增性 A[i] + B[j] > x时 A[i + 1] >= A[i]
所以A[i + 1] + B[j] > x 这些都不满足 不用让j回退
总步数最大为2n 时间复杂度O(N)
*/
for (int i = 0, j = m - 1; i < n; ++i)
{
while (j >= 0 && A[i] + B[j] > x) --j;
if (A[i] + B[j] == x)
{
cout << i << ' ' << j;
break;
}
}
return 0;
}
III 判断子序列

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int b[N];
int main()
{
int n, m;
cin >> n >> m;
int flag = 0;
for (int i = 0; i < n; ++i) cin >> a[i];
for (int i = 0; i < m; ++i) cin >> b[i];
for (int i = 0, j = 0; i < n; ++i)
{
/*j不会往后退*/
while (j < m && b[j] != a[i]) ++j;
if (j == m)
{
cout << "No";
flag = 1;
break;
}
/*走到这肯定是找到了a[i], 匹配掉这个b[j]后
++j*/
++j;
}
if (flag == 0) cout << "Yes";
return 0;
}
2 位运算
I n的二进制表示中的第k位
这里规定个位为第0位。
- 先把n的第k位移动到个位
n >>= k - 看看此时的n个位是几
n & 1 - 综合:
(n >> k) & 1
int main()
{
int n;
cin >> n;
for (int k = 31; k >= 0; --k)
cout << (n >> k & 1);
return 0;
}
II 返回x的最后一位1 lowbit(x)
这里准确的表述应该是返回x的最右边一位1,然后这个1往左都是0,往右也都是0.
lowbit(x) = x & (-x)
原理:C++中,负数都是用补码储存的,所以-x = ~x + 1,设x = A 1 B,B是k个0,则~x = ~A 0 C,C是k个1,~x + 1 = ~A 1 B,x&(~x + 1) = 0 1 B,即我们要的答案。
III 让x的最低位1变成0
x = x & (x - 1),证明类似上面。
IV 二进制中1的个数

思路1:
#include <iostream>
using namespace std;
int lowbit(int x)
{
return x & (-x);
}
int main()
{
int n, x, cnt;
cin >> n;
while (n--)
{
cin >> x;
cnt = 0;
while (x)
{
++cnt;
x -= lowbit(x);
}
cout << cnt << ' ';
}
return 0;
}
思路2:
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int q[N];
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; ++i) cin >> q[i];
for (int i = 0; i < n; ++i)
{
int cnt = 0;
while (q[i] != 0)
{
q[i] &= (q[i] - 1);
++cnt;
}
cout << cnt << ' ';
}
return 0;
}
3 离散化
在一组数据值域很大但是数据个数却不大的情况下,可以使用离散化的技术,所谓的离散化就是把一组数据映射到一组相同个数的连续的自然数,如:1 3 100 2000 500000 -> 0 1 2 3 4.
离散化的两个问题:
- 用到的数据组成的a数组中可能有重复元素,需要排序再去重。
- 如何算出x离散化后的值是多少,由于这时a数组是有序的,直接在a数组中二分查找x的位置即可。
C++去重的库函数,对于一个vector alls,下面的代码可以完成排序加去重。
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin, alls.end()), alls.end());
//unique会把不重复的元素排在前面 重复的元素扔到后面 返回第一个重复的元素的迭代器
//然后erase掉就行
/*映射的过程:*/
int find(const vector<int>& q, int x)
{
int l = 0, r = q.size() - 1;
while (l < r)
{
int mid = (l + r) >> 1;
/*找大于等于x区间的左端点*/
if (q[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1;//映射到1~q.size()
}
例题:

传统思路是我们开一个2 * 1e9个元素的数组,然后用前缀和来处理询问s[r] - s[l - 1],但是请看我们仅有n个插入和m个询问,实际上需要的下标数是n个插入用的n个下标和m次询问用的2m个前缀和下标,n和m都是1e5数量级的,也就是说大概总共会用3* 1e5个下标,完全没有1e10的数量级.
总范围是2 * 1e9,但是我们只用到了3 * 1e5个数,这就是典型的离散化应用场景。
我们可以把用到的下标排个序,保序映射到从1开始的自然数序列。
要给x下标的位置加c,等价于给x的离散化对应的字母k,对a[k] += c;
要查询[l, r]的值的和,把l->k1, r->k2,然后求一下a[k1] + ... +a[k2]即可。
代码:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
//插入n次 询问m次 一共用 n + 2m 级别个下标
//所以离散化后的数组及其前缀和数组开为3 * 1e5级别
const int N = 3 * 1e5 + 10;
int a[N];
int s[N];
vector<int> alls;
vector<PII> adds;
vector<PII> asks;
/*将x映射到它在alls中的下标加1*/
int find(int x)
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = (l + r) >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1;
}
int main()
{
int n, m;
cin >> n >> m;
/*把增加信息入到adds数组中*/
for (int i = 0; i < n; ++i)
{
int x, c;
cin >> x >> c;
adds.push_back({x, c});
}
/*把询问信息入到asks数组中*/
for (int i = 0; i < m; ++i)
{
int l, r;
cin >> l >> r;
asks.push_back({l, r});
}
/*把用到的下标都入到alls里头来
增加下标就作用于映射后的原数组
询问下标就作用于映射后的原数组的前缀和数组
*/
for (int i = 0; i < adds.size(); ++i)
{
alls.push_back(adds[i].first);
}
for (int i = 0; i < asks.size(); ++i)
{
alls.push_back(asks[i].first);
alls.push_back(asks[i].second);
}
/*去重*/
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());
/*处理对应点增加值*/
for (auto e : adds)
{
int x = find(e.first);
a[x] += e.second;
}
/*生成前缀和数组*/
for (int i = 1; i <= alls.size(); ++i)
{
s[i] = s[i - 1] + a[i];
}
/*处理询问*/
for (auto e : asks)
{
int l = find(e.first);
int r = find(e.second);
cout << s[r] - s[l - 1] << endl;
}
return 0;
}
unique函数的实现算法:
vector<int>::iterator unique(vector<int>& a)
{
/*双指针算法 如果第一个指针i指的数满足
i == 0 或 a[i - 1] != a[i]
则a[i]是唯一的元素
*/
int j = 0;
for (int i = 0; i < a.size(); ++i)
{
if (!i || a[i - 1] != a[i])
{
a[j++] = a[i];
}
}
/*最后j指向最后一个不重复的元素的下一位*/
return a.begin() + j;
}
4 区间合并
用途:有很多区间,若几个区间有交集(端点相交也算),则把这几个区间合并为一个比较长的区间。
模板题:

思路:
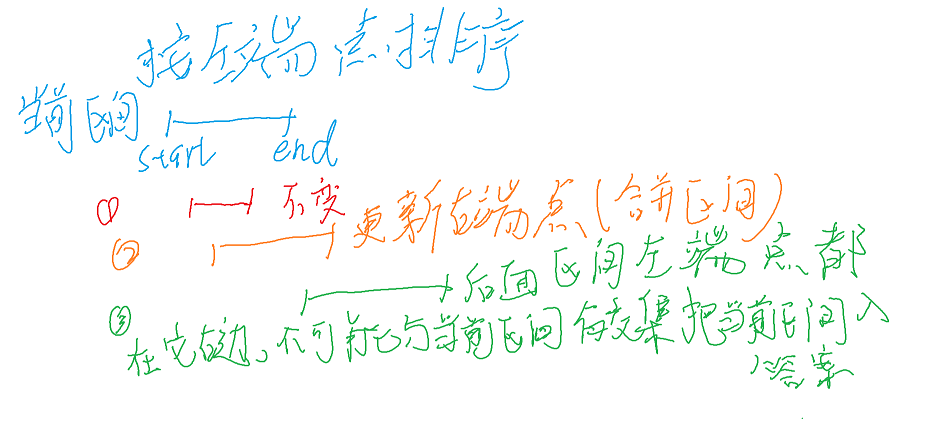
代码:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e6 + 10;
vector<PII> segs;
void merge(vector<PII>& segs)
{
vector<PII> ans;
//先假设一个[-2e9, -2e9]的区间作为起始
int st = -2e9, end = -2e9;
//先排序
sort(segs.begin(), segs.end());
for (auto seg : segs)
{
/*没有交集的情况 把维护的区间入到答案去 更新维护区间为当前区间*/
if (seg.first > end)
{
/*不要把最开始那个东西入进去*/
if (end != -2e9)
{
ans.push_back({st, end});
}
st = seg.first;
end = seg.second;
}
/*有交集则合并 右端点取大*/
else end = max(end, seg.second);
}
/*把最后一个区间也入进去 注意防范segs是空的情况*/
if (end != -2e9) ans.push_back({st, end});
segs = ans;
}
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; ++i)
{
int l, r;
cin >> l >> r;
segs.push_back({l, r});
}
merge(segs);
cout << segs.size() << endl;
return 0;
}






















 2269
2269











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








