傅里叶变换，拉氏变换，Z变换学习笔记

书写动机

由于笔者为大一学生，并未学习过信号有关内容，但如今在阅读GSP(图信号处理)时不得不用到，因此在查阅了部分资料后，将自己想法与大佬们的想法整理成此文，以图加深记忆，作为笔记。

Note:本文为个人笔记，如有侵权请联系我删除或修改！！！

三角函数

如果要了解上述的变换（信号领域），就不得不提到我们的老朋友三角函数。三角函数是我们每个人在初中阶段接触到最可爱的数学工具之一。为什么是可爱的呢？因为它描述了我们生活中最重要的两个基本图形——三角形和圆形，以及第一个无限不循环小数$\pi$.

我们或许早就了解到，三角函数中有两个大名鼎鼎的函数，分别是sin（正弦函数），cos（余弦函数）。使用它们，我们可以求得三角形的边长，求得圆弧的长度，以及通过各种复杂的三角恒等变换来将已有信息转化为渴望求得的信息。

但我们或许也早已发现，这两个函数在本质上或许十分相似。

以至于，我忽然在这里放一张图，你或许分不清这是正弦还是余弦函数。事实上，我们在使用时，将sin与cos统称为正弦函数。

那么，正弦函数究竟有什么实际含义呢？为什么要如此的定义，上文这样的图是如何做出来的呢？
这些问题，我们或许能在初中课本上找到答案，我就由下面一张GIF来说明它们的几何含义。

很明显，当我们让点在固定（y轴上固定，但x轴不断向右平移）圆上运动时，原本枯燥的正弦函数，变成了可爱灵动的正弦波，由函数变为了波，这个变化不可谓不大啊！

正弦波

如今我们已经理解了正弦波，但世间正弦有万千，哪一个才会是我们寻找的呢？为此我们必须好好定义一下它们，防止将它们认错：

• 这个点围绕的圆有多大：振幅
• 这个点围绕速度有多快（相对于周长来说）：角速度——频率
• 这个点的初始位置：相位

有了以上这些基础定义，我们就能区分世界上所有的正弦波了。
当然，我们的数学是时刻秉持用数学语言（公式）描述的学科，因此我们给出正弦波的通用定义：
$f(t)=Asin(\omega t+\phi )+k$

从正弦波到傅里叶

那么说了一大堆三角函数的老掉牙知识，究竟什么是傅里叶变换呢？
其实，学懂了正弦波，你就了解了一半的傅里叶变换。
这句话从何说起呢？还得从原作者傅里叶一句简短却令人振聋发聩的定理开始：

“任何”周期信号都可以用一系列成谐波关系的正弦曲线来表示。

什么意思呢？我们或许在示波器中见过这样的波形

其实它们都是由许多个正弦波简单求和得到的！
在我们先不提其成立条件的前提下，我们任意假设一个波f(t)，其均可以表示为

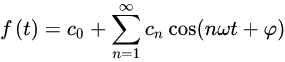
你或许还有所疑惑，可能会问：这又有什么意义呢？不就是把波换了一种形式么？

我得说，这个公式可太厉害了，这叫表明，如果我有一个波f(t)，那么我是不是可能将原波分解，得到每一个正弦波具体的相位，频率和振幅呢？

再通俗一些就是，我们将f(t)理解为一首钢琴曲，原波是在时域上的波形，是一首悠扬的曲子。而分解成的cos(kωt)就是无数个离散的七音符，将它们出现的能量组合就会形成频域的分布。因此，也有人说，乐曲时音乐的时域展现，而乐谱则是音乐的频域展现。

分解原波

好了，上面的饼已经画好了，我们现在已经知道当我们分解原波后会得到多少重要的信息了，那么如何分解原波呢？
此时，我们不得不想到三角函数的正交性了！

即：当两个不同频率的正弦波相乘，对其周期求积分时，结果一定为0.也就是说，不同频率的正弦函数两两正交。

这个概念叫波的相干性，也就是，我想要对一段音频处理，想要知道其中有没有100hz的正弦波，我就用它去乘100hz的正弦波，如果结果不为0，则说明其含有。

如此，我们就可以先将原波分解为下式

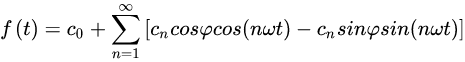
设

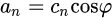
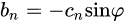
我们可以得到

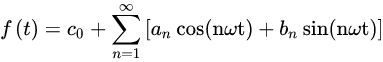
此时，我们将检测波段sin(kωt)加入其中，对其在一个周期内积分：

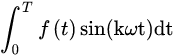
得到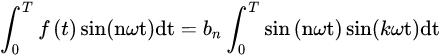
这个结果很自然，因为任何n!=k的正弦波均被滤掉了，仅有n==k的波段留了下来（此处省略大量积分过程，读者可以自主运算）。

然后，将n=k代入式子之中，求出积分，得到：

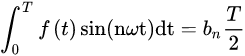
转而，求出bn:

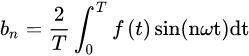
其余量均可以如此求得。
这就是傅里叶变换中的核心傅里叶级数了！
但我们印象中的傅里叶变换好像长这个样子：

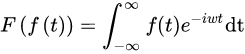
其实，它这是引入了欧拉公式

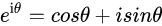
经过简单变换，我们就可以得到它的最初模样

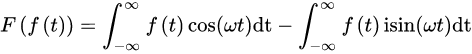
这里引入复频域其实只是为了让sin与cos分离开，方便计算。

拉普拉斯变换

其实上一部分可能读者会有疑问，为什么傅里叶变换针对的“所有”波的“所有”要加引号，其实是因为，它是有前提的。前提就是在任意一个周期中，它的积分均不能等于无穷，如果我们单单按照这个标准，那么一大堆信号均无法处理了。
例如下图：

可以看到，f(t)已经起飞了，可是正弦函数可是有界的，去拟合这样的函数根本不现实，因此，需要一个新的方法去将其转化为有界函数。
至此，拉普拉斯变换横空出世。

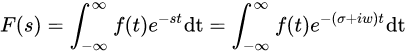
仔细观察我们就能发现，它与傅里叶变换其实只多了一个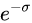
这其实就是将无穷变有界的最终奥义。至此，傅里叶变换的问题得到解决。只要遇到信号，如果有界就傅里叶，没界就拉普拉斯，美哉。

问题出现

但当我们或者上述情绪投入编程任务中时，会发现，sum积分函数，无法使用。因为计算器储存信息是离散的。
不过也没关系，我们将原本连续的波f(t)转化为x[N]∈RN，个离散点。将原本积分换为Σ就好了。

Z变换出现

当我们完成上述工作，就可以将连续信号的傅里叶变换改编为离散形式的傅里叶变换

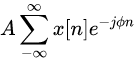
我们令

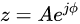
得到

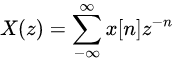
这就是Z变换的基本形式，我们也就完成了时域到频域的转化。

GSP前瞻

前者我们讲了三个基础的变换。在如今信号处理如此重要的今天，如何运用才是关键。

边缘检测

对于计算机视觉任务，边缘检测都是十分重要的步骤之一。只有让模型深入的了解了何处为物体的边缘，模型才能更快的学习到某一类的特征。

• 对于分类任务是某一类的特征；
• 对于分割任务是不通物体语义区别的特征
• 对于超分辨任务是高效聚合高密度信息转化的特征（通俗来说就是给模型指示，去何处提取信息，进而补充分辨率或者光谱数）

有人提出了GSP，将物体用临界权重矩阵表示为两个部分，而权重正是使用的信息频率。

如何获得频率呢？我们可以结合像素离散的特性，将离散傅里叶变换嵌入，使其将空间域（spatial domain）的信息，转化为频域，提取出边缘后，再进行各类操作，进而达到较好的效果。

如今已经有人初步实现了以上的方法，但距离SOTA还具有一些距离，等待发展。