序言
2021年1月
01-01
- 零下五度完成15km跑,用时71’08’’,平均配速4’44’’,其中4km与8km处分别补给了一圈豆奶。我发现只有在极端寒冷的条件下体力消耗才是最少的,之前的两次雨夜12km也是这样跑出来的,这次如果不是10km之后感觉手冷肚子饿,导致选择提速跑到力竭,自信能把4’48’'的配速坚持到20km。
- 倘若到今年12月份能保持住状态且不受伤(事实上这次又把右膝跑伤了),就去报名跑一次上马的半马比赛。
- 标准误差: 指在给定样本:
X
=
{
x
1
,
x
2
,
.
.
.
,
x
n
}
\bm{X}=\{x_1,x_2,...,x_n\}
X={x1,x2,...,xn}的条件下, 样本统计量
T
(
X
)
T(\bm{X})
T(X)的标准差;
- 提供统计推断的一组样本数据, 同样可以用来评估该推断结果的精确性;
- 如样本均值 T ( X ) = x ˉ T(\bm{X})=\bar x T(X)=xˉ, 其标准误差的估计值 s e ^ \widehat{\rm se} se 计算公式为: [ ∑ i = 1 n 1 n 2 V a r ( x i ) ] 1 2 = [ n ⋅ 1 n 2 ⋅ ( x i − x ˉ ) 2 ( n − 1 ) ] 1 2 = [ ∑ i = 1 n ( x i − x ˉ ) 2 n ( n − 1 ) ] 1 2 \left[\sum_{i=1}^n\frac{1}{n^2}{\rm Var(x_i)}\right]^{\frac{1}{2}}=\left[n\cdot\frac{1}{n^2}\cdot\frac{(x_i-\bar x)^2}{(n-1)}\right]^{\frac{1}{2}}=\left[\sum_{i=1}^n\frac{(x_i-\bar x)^2}{n(n-1)}\right]^{\frac{1}{2}} [i=1∑nn21Var(xi)]21=[n⋅n21⋅(n−1)(xi−xˉ)2]21=[i=1∑nn(n−1)(xi−xˉ)2]21
- 最小二乘法中参数 β ^ 0 {\hat\beta}_0 β^0与 β ^ 1 {\hat \beta}_1 β^1的标准误差分别为: s e ( β ^ 0 ) = σ ^ 2 ( 1 n + x ˉ 2 S X X ) s e ( β ^ 1 ) = σ ^ 2 S X X {\rm se}({\hat\beta}_0)={\hat\sigma}^2\left(\frac{1}{n}+\frac{\bar x^2}{\rm SXX}\right)\\{\rm se}({\hat\beta}_1)=\frac{{\hat\sigma}^2}{\rm SXX} se(β^0)=σ^2(n1+SXXxˉ2)se(β^1)=SXXσ^2其中( σ ^ 2 {\hat\sigma}^2 σ^2是最小二乘方差的无偏估计): σ ^ 2 = 1 n − 2 ∑ i = 1 n ( y i − β ^ 0 − β ^ 1 x i ) 2 S X X = ∑ i = 1 n ( x i − x ˉ ) 2 = ∑ i = 1 n x i ( x i − x ˉ ) {\hat\sigma}^2=\frac{1}{n-2}\sum_{i=1}^n(y_i-{\hat\beta}_0-{\hat \beta}_1x_i)^2\\{\rm SXX}=\sum_{i=1}^n(x_i-\bar x)^2=\sum_{i=1}^nx_i(x_i-\bar x) σ^2=n−21i=1∑n(yi−β^0−β^1xi)2SXX=i=1∑n(xi−xˉ)2=i=1∑nxi(xi−xˉ)
01-02
- 投石问路,石沉深海。唉… 新年手贱发了一封邮件,果然是多此一举,罢了。
- 今天恢复了后程提速可以用4’15’'以内的配速完成最后2km的冲刺了。受过几次伤之后慢慢就知道怎么跑是适合的,可惜右膝的伤怕是成了隐疾,昨天又疼一天。
- 假定一组独立同分布样本:
x
i
∼
N
(
θ
,
1
)
i
=
1
,
2
,
.
.
.
,
n
(4.34)
x_i\sim\mathcal{N}(\theta,1)\quad i=1,2,...,n\tag{4.34}
xi∼N(θ,1)i=1,2,...,n(4.34)取
θ
\theta
θ的估计量
θ
^
=
x
ˉ
\hat\theta=\bar x
θ^=xˉ, 观察员通过抛硬币的方式来决定究竟进行多少次采样:
n
=
25
p
r
o
b
a
b
i
l
i
t
y
1
2
n
=
100
p
r
o
b
a
b
i
l
i
t
y
1
2
(4.35)
n=25\quad{\rm probability}\space\frac{1}{2}\\n=100\quad{\rm probability}\space\frac{1}{2}\tag{4.35}
n=25probability 21n=100probability 21(4.35)最终采样结果是
n
=
25
n=25
n=25, 那么问题来了,
θ
^
=
x
ˉ
\hat\theta=\bar x
θ^=xˉ的标准差是多少?
- 如果是 1 / 25 = 0.2 1/\sqrt{25}=0.2 1/25=0.2, 那么费雪就会赞成你, 这是一个条件推断;
- 如果是 [ ( 0.01 + 0.04 ) / 2 ] 1 / 2 = 0.158 [(0.01+0.04)/2]^{1/2}=0.158 [(0.01+0.04)/2]1/2=0.158, 这就是非条件的频率学派做出的回答;
01-03
- 考虑到明天会下雨, 于是选择今天再进行一次长跑,但是下午风大,而且出了太阳,气温回升,25圈就完全力竭了,平均配速4’45"。可能还是起步太急,15km那次起手才5’15"(今天是4’55"),还是穿着厚大衣跑的,最后还跑回了4’44"的平均配速。总之离能稳定跑半马还有很长路要走的。
- 结果前天的发的邮件最终还是收到回复了… SXY一直在实习,似乎并没有读博的打算。总是试图去忘记,却无奈地发现自己始终只是在躲避,何等荒唐。
- 逻辑回归(logistic regression)是一种专门用于频数或频率型数据的回归分析方法; 其中的logit参数 λ \lambda λ定义为: λ = log { π 1 − π } (8.4) \lambda=\log\left\{\frac{\pi}{1-\pi}\right\}\tag{8.4} λ=log{1−ππ}(8.4)其中 π \pi π为计数事件发生的频率, 即二项分布 B i ( n , p ) Bi(n,p) Bi(n,p)中的概率参数 p p p; 当 π \pi π从 0 0 0变化到 1 1 1时, logit参数 λ \lambda λ从 − ∞ -\infty −∞变化到 + ∞ +\infty +∞;
- 究其本质, 逻辑回归就是假设应变量 π \pi π与自变量 x x x间的关系并非线性, 因此构造 λ \lambda λ使得 λ \lambda λ与 x x x之间的存在线性关系, 然后通过拟合 λ \lambda λ与 x x x, 再根据 λ \lambda λ与 π \pi π之间的关系来解决 π \pi π与 x x x之间的回归方程;
- 从结果上来看, 逻辑回归的目标函数是最小化Kullback–Leibler距离; 因此也是可以与Lasso回归等添加正则项的方法相结合; 本质上逻辑回归中的训练参数与线性回归中的训练参数是一致的, 正则项可以设为待定参数的某种模数;
- 逻辑回归是广义线性模型的一种特殊情况;
- 逻辑回归中的link function是:
g
(
y
)
=
e
y
e
y
+
1
g(y)=\frac{e^y}{e^y+1}
g(y)=ey+1ey
- link function的反函数称为logit function: g − 1 ( θ ) = log { θ 1 − θ } g^{-1}(\theta)=\log\left\{\frac{\theta}{1-\theta}\right\} g−1(θ)=log{1−θθ}其中 θ 1 − θ \frac{\theta}{1-\theta} 1−θθ称为odds;
- 估计参数 θ \theta θ的表达式可以写作: θ ( X ) = g ( X β ) = e X β 1 + e X β = 1 1 + e − X β \theta(\bm{X})=g(\bm{X}\beta)=\frac{e^{\bm{X}\beta}}{1+e^{\bm{X}\beta}}=\frac{1}{1+e^{-\bm{X}\beta}} θ(X)=g(Xβ)=1+eXβeXβ=1+e−Xβ1
01-04
- 王英林给我找了个离谱的合作课题,鼎捷软件那边要做一个APP的个性化UI设计,居然想用机器学习来学习各种不同的UI来做智能化的UI排版。我细想了一会儿感觉这活实在是太扯了,不过还是等周三周四去公司实地考察一下再说。
- 不管怎么样,有活干总是件好事,等王明这辈博士学长毕业,下一个门面担当舍我其谁,始终还想在学生时代再狂几年。
- 右脚跟腱似乎出了些问题,这两个月右下肢从大腿根到脚底都废了一遍,不过晚上还是冒雨10圈加速跑,感觉状态不太好,要休整一两日回口血了。
- The plug-in principle:
- 用原模型分布产生的数据分布来估算模型本身的分布, 然后将预估出来的参数插入到原分布中以做出最优预测;
- 如可以将分布 F F F下的样本均值 X ˉ = ∑ X i n \bar X=\frac{\sum X_i}{n} Xˉ=n∑Xi的标准误差与 v a r F ( X ) {\rm var}_F(X) varF(X)联系起来: s e ( X ˉ ) = [ v a r F ( X ) n ] 1 2 (2.8) {\rm se}(\bar X)=\left[\frac{{\rm var}_F(X)}{n}\right]^{\frac{1}{2}}\tag{2.8} se(Xˉ)=[nvarF(X)]21(2.8)我们只有观测到的样本数据 x = ( x 1 , x 2 , . . . , x n ) \bm{x}=(x_1,x_2,...,x_n) x=(x1,x2,...,xn), 于是只能进行估计: v a r ^ F = ∑ ( x i − x ˉ ) 2 n − 1 (2.9) {\widehat {\rm var}}_F=\sum\frac{(x_i-\bar x)^2}{n-1}\tag{2.9} var F=∑n−1(xi−xˉ)2(2.9)将Formula 2.9嵌入到Formula 2.8中就可以得到Formula 1.2中的估计值 s e ^ \widehat{\rm se} se ;
- 拓展:
- ① 如 θ = E ( X ) \theta=E(X) θ=E(X)的估计量为 ∑ i = 1 n X i n \frac{\sum_{i=1}^nX_i}{n} n∑i=1nXi, 通过R-S Integral可以知道 θ = E ( X 2 ) \theta=E(X^2) θ=E(X2)的估计量为 ∑ i = 1 n X i 2 n \frac{\sum_{i=1}^nX_i^2}{n} n∑i=1nXi2
- ② 关于 v a r ( X ˉ ) {\rm var}(\bar X) var(Xˉ)的估计值, 可以使用 v a r ( X ˉ ) = σ 2 n = 1 n { ∫ x 2 d F ( x ) − [ x d F ( x ) ] 2 } {\rm var}(\bar X)=\frac{\sigma^2}{n}=\frac{1}{n}\left\{\int x^2{\rm d}F(x)-\left[x{\rm d}F(x)\right]^2\right\} var(Xˉ)=nσ2=n1{∫x2dF(x)−[xdF(x)]2}, 则可以得到: v a r ^ ( X ˉ ) = 1 n { ∫ x 2 d F n ( x ) − [ x d F n ( x ) ] 2 } \widehat {\rm var}(\bar X)=\frac{1}{n}\left\{\int x^2{\rm d}F_n(x)-\left[x{\rm d}F_n(x)\right]^2\right\} var (Xˉ)=n1{∫x2dFn(x)−[xdFn(x)]2}
01-05
- 连肝五天,终于把这学期的统计课从头到尾细细过了一遍,【学习笔记】计算机时代的统计推断可能真的只能挑几个章节写一下了,我发现看李卫明的Slide到Chapter11和12讲到bootstrap还有交叉验证的时候完全已经看不懂里面的推导,结论也很难记住,大后天考到只能认栽。
- 我计划是把前12章每个章节做一下重点汇总,主要还是应付考试。后面主要是17-19这三个章节可能会详细写一下,因为确实是很流行的三种方法(Random Forests,Neural Networks,SVMs),也很想细致得了解一下里面的统计原理,其他几个章节只能随缘,实在是太难了。
- 右脚跟腱好像真的有点隐疼,但是跑起来也感觉不到疼痛,晚上前五圈很谨慎地以5分以上的配速跑,后五圈把平均配速跑回4’36",结果一点疼痛感也没有,这跟腱就很迷,不知道是怎么回事。
- 这学期结束,转回管科的话,软工这儿的人以后也难碰面了… 人和事都无疾而终,大约还是要重新开始。
- 神经网络概述:
- 20世纪80年代, 神经网络的提出震惊了应用统计学界;
- 神经网络是一种高度参数化的(highly parametrized)模型;
- Figuer 18.1中是最简单的前馈神经网络示意图:
- 其中模型输入包含4个预测因子(predictors), 隐层节点共计5个, 最终输出为单个标量值; 具体计算公式如下:
- 模型输入张量: ( x 1 , x 2 , x 3 , x 4 ) (x_1,x_2,x_3,x_4) (x1,x2,x3,x4)
- 计算隐层状态: a l = g ( w l 0 ( 1 ) + ∑ j = 1 4 w l j ( 1 ) x j ) a_l=g(w_{l0}^{(1)}+\sum_{j=1}^4w_{lj}^{(1)}x_j) al=g(wl0(1)+∑j=14wlj(1)xj)
- 计算输出标量: o = h ( w 0 ( 2 ) + ∑ l = 1 5 w l ( 2 ) a l ) o=h(w_0^{(2)}+\sum_{l=1}^5w_l^{(2)}a_l) o=h(w0(2)+∑l=15wl(2)al)
- 上述公式中:
- 称 g g g与 h h h为激活函数, 通常为非线性函数; 常见的激活函数有Sigmoid, ReLU, Softmax;
- 称 a l a_l al称为神经元(neurons); 神经元从数据中学习新特征的过程称为监督学习(supervised learning);
- 每个神经元通过训练参数 { w l j ( 1 ) } 1 p \{w_{lj}^{(1)}\}_1^p {wlj(1)}1p相互联系, 其中上标 ( 1 ) (1) (1)表示这是第 1 1 1层, 下标 l j lj lj表示这是第 j j j个变量的第 l l l个训练参数; 特别地, 截距项 w l 0 ( 1 ) w_{l0}^{(1)} wl0(1)称偏差(bias);
- 其中模型输入包含4个预测因子(predictors), 隐层节点共计5个, 最终输出为单个标量值; 具体计算公式如下:
- 本质上神经网络就是一种非线性模型, 与其他线性模型的推广(广义线性模型等)并没有什么区别, 但是它确实给学界注入新鲜能量;
- 20世纪90年代, 随着boosting方法(Chapter 17)与支持向量机(Chapter 19)的兴起, 神经网络由于其解释性的缺乏逐渐没落;
- 2010年之后, 神经网络又突然以深度学习(deep learning)的身份重生, 再次制霸各类分类预测领域, 如图像与音像数据分类, 自然语言处理等;
01-06
- 考前焦虑,什么事情也做不成,颓废了一天。
- 前天刷完了《小魔女学园》,一部非常好的番剧,很久不补番,这部还是半年前开始看的,但是确实是很出乎意料的精彩。好想就这样无忧无虑地补补番唉。
- 各种奇怪的markdown公式括号写法:

01-07
- 昨晚到今早花了五六个小时终于把大一C++课的期末考卷改完,惨不忍睹,除了一个96分,两个85分,其他都在80以下,一半的人不及格,就看最后怎么调分了。我真的是一肚子火,学了半年,好多人连最基本的条件和循环都分不清,平时作业各种雷同,还都是计科班的,这届新生质量真的很差。
- 下午去鼎捷调研,来回骑车10公里,大顶风不谈,关键是真的冻死了,在上海待了五年,第一次冬天这么冷,废了。不过接下来要搞智能用户界面,这不是一件容易的事情,如果只有我们硕士做可能问题会比较大。
- 费雪学派的方法论因为过度依赖正态样本的假设而被批判;
- 以之前提到的白血病案例, 47个 A L L \rm ALL ALL与25个 A M L \rm AML AML患者(Figure 1.1), 两样本 t t t检验的结果为 t t t值3.13, 双侧显著水平为 0.0025 0.0025 0.0025, 这些都是基于高斯或者正态的假设;
- 费雪提出使用置换方法处理这72个患者样本, 即每次随机分为47个和25个的不相交集合, 然后重复
B
B
B次
t
t
t值计算, 得到了
B
B
B个不同的
t
t
t值序列
t
1
∗
,
t
2
∗
,
.
.
.
,
t
B
∗
t_1^*,t_2^*,...,t_B^*
t1∗,t2∗,...,tB∗, 则双侧置换显著水平就是:
c
o
u
n
t
(
{
∣
t
i
∗
∣
≥
t
}
)
B
\frac{{\rm count}(\{|t_i^*|\ge t\})}{B}
Bcount({∣ti∗∣≥t})
- 即是多次实验取均值, 这样得出的结果是 t t t值3.13, 置换显著水平为 0.0022 0.0022 0.0022
- 费雪对置换显著水平的可信度做出解释:
- 假设我们零下架是72个独立同分布的样本: x i ∼ f μ ( x ) i = 1 , 2 , . . . , n x_i\sim f_\mu(x)\quad i=1,2,...,n xi∼fμ(x)i=1,2,...,n这里没有正态假设, 但是我们还是默认 f μ ( x ) f_\mu(x) fμ(x)就是 N ( θ , σ 2 ) \mathcal{N}(\theta,\sigma^2) N(θ,σ2);
- 假设 o \bm{o} o是观测样本集合 x \bm{x} x的次序统计量, 不妨设是从小到大排列的结果, 然后去除了各自的 A L L \rm ALL ALL和 A M L \rm AML AML标签; 那么就有 72 ! / ( 47 ! 25 ! ) 72!/(47!25!) 72!/(47!25!)中方法通过划分 o \bm{o} o成为不相交的子集(子集元素个数分别为47与25个), 来获得 x \bm{x} x, 且这些概率是相同的;
01-08
- 统计考完,感觉写得还是比较顺的,结果应该不会太辣眼睛。
- 恢复常态,这几天因为考试确实是颓废得很。重新开始从4km跑,不过确实是冷,阳台水池和拖把都冻住了,风也很大,不过按照之前得经验,明天会是个长跑的好天气,今晚养精蓄锐。
- 这样一来就彻底结束了,接下来真的是和软工再无牵扯了,实话说自己还是有些遗憾的,多少还是认识了几个人,这么快就又要断了。
- 多进程模块:
class multiprocessing.Process(group=None, target=None, name=None, args=(), kwargs={}, *, daemon=None):
- 实例化对象:
process = Process(target=f, args=(1, )); - 对象方法:
process.run(): 直接运行该进程, 即执行f(1);process.start(): 进程准备就绪, 等待调度;process.terminate(): 终止进程(发出SIGTERM信号);process.kill(): 杀死进程(发出SIGKILL信号);process.close(): 关闭进程;- 若该进程的当前进程存在处于运行状态的子进程时, 调用则会报错;
process.join(timeout=None):- 若
timeout是None, 则该方法将阻塞, 直到join()调用其方法的进程终止; - 若
timeout是一个正数, 它最多会阻塞timeout秒; - 若方法的进程终止或方法超时, 则返回该方法;
- 可以检查进程的
process.exitcode以确定它是否终止; - 所谓阻塞, 就是需要等方法完全执行完毕才会让其他进程工作, 非阻塞即可以异步执行(效果上是同时执行)不同的进程;
- 若
process.name: 进程名称;process.is_alive(): 进程是否存活;- 从
start()方法返回到子进程终止的那一刻, 进程对象将处于活动状态;
- 从
process.daemon: 进程的守护进程标志;- 默认值
False; - 必须在
start()调用之前设置; - 若设置为
True, 当进程退出时, 它会尝试终止其所有守护进程子进程;
- 默认值
process.pid: 进程ID;process.exitcode: 进程的退出代码;- 如果进程尚未终止, 则返回
None; - 否则返回
-N, 表示进程被信号N终止;
- 如果进程尚未终止, 则返回
01-09
- 寒假开始,下午长跑,发现右脚跟腱更疼了,明明已经休息了两天,一踮脚就疼,本是奔着20km去跑的,最后只跑了10km就撤了,一旦提速就会有刺痛感,太不便了,得多泡脚看看能不能恢复得过来。
- 从昨晚开始上手之前一直想写的三国杀单挑仿真项目,初始灵感是想要测试四血界孙权单挑四血新王异在不同状态下的优劣(如新王异零装备起手,单+1马起手,+1马和藤甲/仁王盾起手,单雌雄剑起手,单木牛流马起手),后续是想使用强化学习方法进行训练得出界孙权的最优打法,之前听说过四血标孙权可以和四血新王异五五开,以为界孙权的容错会相对高一些,但是看了去年老炮杯一局经典的界孙权内奸单挑主公新王异,界孙权实在是真的是太被动了(当然那时候新王异已经神装雌雄+木马了,界孙权几乎没有任何机会,但是最后还是界孙权竟然没有靠闪电就完成翻盘,虽然只是险胜。我个人的感觉是王异只要有雌雄剑和+1马基本上就可以一战了,如果摸到木牛流马王异几乎必胜),这个单挑对于界孙权来说要比想象中的困难得多,因为能针对新王异的卡牌就只有三张乐不思蜀,而且木马本质上对于界孙权来说只能存一张牌。
- 目前已经把除出牌阶段的逻辑都写完了,预计明天可以基本完成。
摘自https://caoyang.blog.csdn.net/article/details/109139934
- 使用掩码蒙蔽(mask blinding)的特征加密:
- 为保全特征值的隐私, 本文使用一个带有模加(modular addition)随机掩码来蒙蔽每个特征值, 从而将这个值隐藏起来让服务器无法获得;
- 随机掩码使用一个PRF确定性地生成, 只对客户端可知;
- 每个特征值
f
f
f在索引中以
[
f
+
R
]
[f+R]
[f+R]被存储起来:
- 其中 [ f + R ] = ( f + R ) ( m o d N ) [f+R]=(f+R)(mod\space N) [f+R]=(f+R)(mod N)
-
R
R
R是一个被计算成项目编号和文档编号的PRF值的特征掩码(feature mask), 取值范围为
{
0
,
1
,
2
,
.
.
.
,
N
−
1
}
\{0,1,2,...,N-1\}
{0,1,2,...,N−1}
- 备注: 理解为随机噪声
- N N N在本文的实现中被设置为常数 2 32 2^{32} 232
- 中括号表示的 [ f + R ] [f+R] [f+R]也强调服务器只能看到 ( f + R ) ( m o d N ) (f+R)(mod\space N) (f+R)(mod N), 而不能知道 f f f与 R R R的具体值;
- 如果折衷且明智地选择掩码, 上面的schema将允许服务器通过累和掩码特征值来计算排序得分, 从而可以进行部分比较(partial comparison);
- 本文没有采用一个同态加密schema来进行特征蒙蔽(feature blinding), 因为这不能带来可见的优势但却更加低效, 且不能支持服务端的部分排序(partial ranking);
- 具体来说, 对于文档
d
d
d, 索引中的特征权重
f
i
d
f_i^d
fid是一个整数, 并且使用随机噪声掩码
R
i
d
R_i^d
Rid处理后以
[
f
i
d
+
R
i
d
]
[f_i^d+R_i^d]
[fid+Rid]存储; 可以引入一个可选的权重
O
t
d
O_t^d
Otd即存储成
[
O
t
d
+
R
O
t
d
]
[O_t^d+RO_t^d]
[Otd+ROtd], 这里的随机噪声掩码是
R
O
t
d
RO_t^d
ROtd;
- 给定一个带有 q q q个必选特征的查询和 m m m个可选的权重, 对于包含这些掩码的文档 d d d排序总分(total rank score) F F F加上总分掩码(total score mask)模 N N N的结果是: [ F + M ] = [ ∑ i = 1 q [ f i d + R i d ] + ∑ 1 ≤ t ≤ m , O t ∈ X [ O t d + R O t d ] ] [F+M]=[\sum_{i=1}^q[f_i^d+R_i^d]+\sum_{1\le t\le m, O_t\in X}[O_t^d+RO_t^d]] [F+M]=[i=1∑q[fid+Rid]+1≤t≤m,Ot∈X∑[Otd+ROtd]]
- 其中 M = ∑ 1 ≤ t ≤ m , O t ∈ X O t d + ∑ 1 ≤ t ≤ m , O t ∈ X R O t d M=\sum_{1\le t\le m, O_t\in X}O_t^d+\sum_{1\le t\le m, O_t\in X}RO_t^d M=∑1≤t≤m,Ot∈XOtd+∑1≤t≤m,Ot∈XROtd
- O t ∈ X O_t\in X Ot∈X表示对应的可选特征可以在索引的键值对存储中找到;
- 虽然服务器可以计算上面的加密总和, 但是不同文档里的特征掩码是随机且相互独立的, 所以服务器是不能比较所有匹配到的文档中的相对排名次序;
- 当服务器匹配到的文档数量适中时, 服务器可以将这些结果发送给客户端, 顺带发送一个用在每个文档里的可选特征的位图(bitmap), 这个位图可以用来协助客户端移除每个排序得分中的掩码总和;
- 备注:
- 位图: 就是用每一位来存放某种状态, 适用于大规模数据, 但数据状态又不是很多的情况, 通常是用来判断某个数据存不存在的; 这里应该就是表示文档是否被匹配;
- 备注:
- 当服务器匹配到的文档数量非常大时或C/S带宽很小, 本文想要服务器进行部分排序从而使得有低分的结果先被过滤掉, 就可以不用发送给客户端; 本质上这变成了一个两阶段的排序, 是cascade ranking的一种类型;
- 当服务器匹配到的文档数量适中时, 服务器可以将这些结果发送给客户端, 顺带发送一个用在每个文档里的可选特征的位图(bitmap), 这个位图可以用来协助客户端移除每个排序得分中的掩码总和;
01-10
- 算是白忙活了个周末,我觉得一个人真的很难写完三国杀单挑测试脚本,我为了减少工作量已经没有继承BaseCard给每张卡牌写单独的子类,但是即便如此,规则定义还是过于费时,就单单无懈可击结算就足以让我抓狂。
- 我已经把代码挂到博客里,其实我觉得已经完成了八成的工作量了,剩余很多东西主要是需要多次人机交互,导致写提示语非常繁琐,除了非延时类锦囊外其他卡牌的用法都已经定义好了,虽然最近似乎还挺闲,但也不太愿意花再多时间在非本业的工作了,希望以后能有机会回头把代码全部写完。但愿…
- 唉,真是无奈。
- 三国杀牌堆类:
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
import random
from example_config import CardConfig, DeckConfig
from example_base import BaseCard
from example_utils import *
class Deck(object):
def __init__(self, cards: list=None, discards: list=None) -> None:
if cards is None: # 没有给定
self.load_default_deck()
else: # 否则直接使用给定的卡牌创建新牌堆
self.cards = cards
# random.shuffle(self.cards) # 洗牌
self.discards = [] if discards is None else discards # 初始化弃牌堆
self.id2card = {card.id: card for card in self.cards} # 构建一个卡牌的索引, 便于查询
def load_default_deck(self) -> None:
"""默认军争牌堆(带木牛流马, 161张牌)"""
self.cards = []
cardconfig_dict = get_config_dict(CardConfig)
index = -1
with open(DeckConfig.default_deck_filepath, 'r', encoding='utf8') as f:
lines = f.read().splitlines()
# default_deck_filepath配置文件的数据处理
for line in filter(None, lines): # 注意删除配置文件中的空行
entry = line.strip()
if entry.startswith('[') and entry.endswith(']'): # 花色名称包含在'['与']'之间
suit = CardConfig.__getattribute__(CardConfig, cardconfig_dict.get(entry[1:-1]))
else: # 其他每行都是点数与花色相同的数张卡牌名称
cells = entry.split('|') # 每行的数据使用'|'分隔
point = cells[0] # 点数位于行首
for cell in cells[1:]: # 其他位置都是卡牌名称
name = CardConfig.__getattribute__(CardConfig, cardconfig_dict.get(cell))
first_class, second_class, attack_range = CardConfig.name2attr.get(name)
index += 1
kwargs = { # 新卡牌的参数
'id': index,
'name': name,
'first_class': first_class,
'second_class': second_class,
'suit': suit,
'point': point,
'attack_range': attack_range,
}
card = BaseCard(**kwargs) # 创建新卡牌
self.cards.append(card) # 将新卡牌添加到牌堆中
def refresh(self) -> None:
"""更新牌堆"""
random.shuffle(self.discards) # 弃牌堆洗牌
self.cards.extend(self.discards) # 将洗好的弃牌堆卡牌添加到牌堆下面
self.discards = [] # 置空弃牌堆
if __name__ == '__main__':
deck = Deck()
index = 0
for card in deck.cards:
index += 1
print(index, card.suit, card.point, card.name, card.first_class, card.second_class, card.area, card.attack_range)
01-11
- 颓废半天,上分不成,白白浪费一个下午。
- 现在如果不是在做分内的事就特别罪恶,但是有时候还就是想去花很长时间做一件看起来确实没啥意义的事情,总结还是被生活毒打得不够。
- 晚上随性跑了10圈,明天养个状态跑10km清醒一下,8号考完试后已经不务正业整整三天了,再这么下去怕是真的没了。
- 三国杀测试脚本的工具函数:
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
from example_config import CardConfig
def get_config_dict(config: type) -> dict:
"""获取配置类的参数字典(键值反转)"""
config_dict = {}
for key in dir(config):
if key.startswith('__') and key.endswith('__'):
continue
try:
config_dict[config.__getattribute__(config, key)] = key
except:
continue
return config_dict
def display_card(card) -> None:
if card is None:
print(card)
else:
print(card.id, card.suit, card.point, card.name)
def display_character(character) -> None:
print(' - 体力值: {}'.format(character.health_point))
print(' - 体力上限: {}'.format(character.health_point_max))
print(' - 手牌区: {}张'.format(len(character.hand_area)))
for card in character.hand_area:
print(' + ', end='')
display_card(card)
equipment_count = 0
for card in character.equipment_area.values():
if card is not None:
equipment_count += 1
print(' - 装备区: {}张'.format(equipment_count))
for area, card in character.equipment_area.items():
print(' + {}: '.format(area), end='')
display_card(card)
print(' - 判定区: {}张'.format(len(character.judgment_area)))
for card in character.judgment_area:
print(' + ', end='')
display_card(card)
def fetch_cards(deck, number: int=1, from_top=True) -> list:
"""从牌堆获取若干张卡牌"""
if len(deck.cards) < number:
print(' - 触发洗牌')
deck.refresh()
if len(deck.cards) < number:
raise Exception('平局')
cards = [deck.cards.pop(0 if from_top else -1) for _ in range(number)]
return cards
def recast_card(deck, card):
"""重铸卡牌"""
new_card = fetch_cards(deck=deck, number=1)[0]
deck.discards.append(card)
return new_card
def hurt(deck, character, hurt_point: int=1):
"""受到伤害"""
armor = character.equipment_area[CardConfig.armor]
if armor is not None and armor.name == CardConfig.bysz: # 白银狮子减伤
hurt_point = 1
character.health_point -= hurt_point
if character.health_point <= 0:
character.ask_for_peach(deck, mode='manual')
def calc_distance(source_character, target_character, base: int=1) -> int:
"""计算距离"""
return max(1, base - (source_character.equipment_area[CardConfig.attack_horse] is not None) + (target_character.equipment_area[CardConfig.defend_horse] is not None))
def calc_attack_range(character):
"""计算攻击范围"""
if character.equipment_area[CardConfig.arms] is None:
return 1
return character.equipment_area[CardConfig.arms].attack_range
if __name__ == '__main__':
pass
01-12
- 统计85分卡点3.7,刺激,拼了五天终究不负,状态振奋。
- 考虑到论文不可能每篇都详读,从今天起新设一块专门放论文略读的笔录,以表格记录。
- 下午大破10km成绩,去年十一月底的46’42",今天提升到了45’53"。上一个pb跑完废了左脚,后来又陆续废了右脚,右膝,到最近废了右跟腱,今天天气非常好,不冷不热,维持4’40"配速到20圈状态都保持得很好,然后决定提速跑10km,因为感觉再跑个15km太费时了,而且可能这个速度坚持不到15km。最后5圈把平均配速提到4’35"以内,历史最好成绩,很舒爽。也许是受今天统计考试成绩的鼓舞吧,哈哈!
- DGL库图节点分类示例代码:(我看THU数据派的推文好像清华那边也开发了一个开源的Python包AutoGL,跟DGL差不多也是做图神经网络这块的,延展性也很好,不过真的有必要学习这么多用途相近的package吗,人的精力还是有限的)。
# -*- coding: UTF-8 -*-
import dgl
import torch
import numpy as np
import dgl.nn as dglnn
import torch.nn as nn
import torch.nn.functional as F
# Load data.
dataset = dgl.data.CiteseerGraphDataset()
graph = dataset[0] # num_nodes: 3327 | num_edges: 9228
# Contruct a two-layer GNN model.
class SAGE(nn.Module):
def __init__(self, in_feats, hid_feats, out_feats):
super().__init__()
self.conv1 = dglnn.SAGEConv(in_feats=in_feats, out_feats=hid_feats, aggregator_type='mean')
self.conv2 = dglnn.SAGEConv(in_feats=hid_feats, out_feats=out_feats, aggregator_type='mean')
def forward(self, graph, inputs): # inputs are features of nodes
h = self.conv1(graph, inputs)
h = F.relu(h)
h = self.conv2(graph, h)
return h
node_features = graph.ndata['feat'] # Node feature: shape(3327, 3703)
node_labels = graph.ndata['label'] # Node labels: shape(3327, )
train_mask = graph.ndata['train_mask'] # Train mask: shape(3327, ), used to drop some nodes
valid_mask = graph.ndata['val_mask'] # Valid mask: shape(3327, ), used to drop some nodes
test_mask = graph.ndata['test_mask'] # Test mask: shape(3327, ), used to drop some nodes
n_features = node_features.shape[1] # Number of features: 3703
n_labels = int(node_labels.max().item() + 1) # Number of different classes: 6
# Define model metric.
def evaluate(model, graph, features, labels, mask):
model.eval() # Enter the evaluation mode.
with torch.no_grad(): # When we do evaluation, gradient is not needed to be considered.
logits = model(graph, features) # Get the output of the model.
logits = logits[mask] # Predicted possibility.
labels = labels[mask] # True labels.
_, indices = torch.max(logits, dim=1) # Get the index of max possibility.
correct = torch.sum(indices == labels) # Get the number of correct prediction.
return correct.item() * 1.0 / len(labels) # Calculate accuracy.
# Train model.
model = SAGE(in_feats=n_features, hid_feats=100, out_feats=n_labels)
opt = torch.optim.Adam(model.parameters())
for epoch in range(100):
model.train()
logits = model(graph, node_features)
loss = F.cross_entropy(logits[train_mask], node_labels[train_mask])
acc = evaluate(model, graph, node_features, node_labels, valid_mask)
opt.zero_grad()
loss.backward()
opt.step()
print(loss.item(), acc)
print('Accuracy on test: {}'.format(evaluate(model, graph, node_features, node_labels, test_mask)))
# Save model.
torch.save(model, 'node_sage.m')
01-13
- 转硕博要补第一学期的课,于是我赶紧去问ss和yy要优化理论的课件资料,以及期中期末的考卷,怕过段时间他们就全忘了。然后这俩货笑我还要这玩意儿,说哪有什么课件,他们自己用的课件就是我给他们整理的本科高级运筹学课件,我直接打出三个问号???
- 压力山大,每次开完会都觉得自己跟个废柴一样,但是总是躲不过间歇性踌躇满志综合征,只有在跑步中才能逐渐从迷失中寻回自我,跑步已经越来越化为我生命中无法割裂的一部分了。
- 这学期总体来说不算太差,虽然没有实习或者做助管搞副业来充实口袋,但是坚持跑步并且达到了从前不曾企及的水平,绩点马马虎虎有3.79多(全靠期末统计力挽狂澜,英语实在是一生之敌),然后也忙里偷闲在导师主持的会议论文集中发了一篇水文。接下来两个学期课非常多,到时候还有转博考和博资考,还是要抓紧空闲时间,一切提早准备才能顺利毕业。研路漫漫,善始善终,且与诸君共勉。
- python带参数的装饰器写法:
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
import time
from functools import wraps
def timer(func):
@wraps(func)
def wrapper(*args, **kwargs):
start_time = time.time()
func(*args, **kwargs)
end_time = time.time()
print('Function `{}` runtime is {} seconds.'.format(func.__name__, end_time - start_time))
return wrapper
@timer
def mytest(n):
for i in range(n):
time.sleep(.01)
if __name__ == '__main__':
mytest(1000)
01-14
- 最近在重看transformer,准备用torch和tensorflow分别写个demo,以后总能用得到,正好也是回顾一下Transformer中的原理,感觉还是很有必要重看的,很多都忘了。
- 午睡时不知为何心跳很快,特别紧张,完全睡不着,近期也没什么特别的事情。
- 下午状态也不行,上场只跑了10圈,不过拼了半条命跑进了18分钟,基本持平了pb,有点热,明天再试试能不能到20km。
- PyTorch版本的Positional Encoding
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
# Implementation for *Attention is all you need*
# Paper download: https://arxiv.org/abs/1706.03762.pdf
import torch
import numpy
class PositionalEncoding(torch.nn.Module):
"""Section 3.5: Implementation for Positional Encoding"""
def __init__(self, d_input: int, d_output: int, n_position: int) -> None:
"""
Transformer takes the position index of element in a sequence as input features.
Positional Encoding can be formulated as below:
$$
{\rm PE}({\rm pos}, 2i) = \sin\left(\frac{\rm pos}{10000^{\frac{2i}{d_{\rm model}}}}\right) \\
{\rm PE}({\rm pos}, 2i+1) = \cos\left(\frac{\rm pos}{10000^{\frac{2i}{d_{\rm model}}}}\right)
$$
where:
- $\rm pos$ is the position index of element.
- $i$ is the index of embedding vector of `PositionalEncoding`.
:param d_input : Input dimension of `PositionalEncoding` module.
:param d_output : Output dimension of `PositionalEncoding` module.
:param n_position : Total number of position, that is the length of sequence.
"""
super(PositionalEncoding, self).__init__()
def _generate_static_positional_encoding():
sinusoid_table = numpy.array([[pos / numpy.power(10000, (i - i % 2) / d_output) for i in range(d_output)] for pos in range(n_position)])
sinusoid_table[:, 0::2] = numpy.sin(sinusoid_table[:, 0::2])
sinusoid_table[:, 1::2] = numpy.cos(sinusoid_table[:, 1::2])
return torch.FloatTensor(sinusoid_table).unsqueeze(0) # Unsequeeze: wrap position encoding tensor with '[' and ']'.
self.linear = torch.nn.Linear(in_features=d_input, out_features=d_output)
self.register_buffer('pos_table', _generate_static_positional_encoding())
# print(self.pos_table.shape) # (1, `n_position`, `d_output`)
def forward(self, input: torch.FloatTensor) -> torch.FloatTensor:
"""
Add static postional encoding table to input tensor for output tensor.
:param input: The shape is (*, `n_position`, `d_input`)
:return position_encoding: The shape is (*, `n_position`, `d_output`)
"""
x = self.linear(input) # (*, `n_position`, `d_output`)
position_encoding = x + self.pos_table[:, :x.shape[1]].clone().detach()
return position_encoding # (*, `n_position`, `d_output`)
01-15
- CSDN年度之战榜单
- 一共700多人参赛,一等奖5个,二等奖10个,前15里面除我之外全是博客专家,90%的粉丝过千,征文点赞和收藏都是至少两位数,而我只有4点赞1收藏,那个收藏还是我自己点的。什么叫以质取胜啊[战术后仰]
- 可把我给牛逼的[哈哈]
- PyTorch版本的Position-wise Feed-Forward Networks
class PositionWiseFeedForwardNetworks(torch.nn.Module):
"""Section 3.3: Implementation for Position-wise Feed-Forward Networks"""
def __init__(self, d_input: int, d_hidden: int) -> None:
"""
The Position-wise Feed-Forward Networks can be formulated as below:
$$
{\rm FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2
$$
Note:
- Input dimension is the same as output dimension, which is set as $d_{\rm model}=512$ in paper.
- Hidden dimenstion is set as $\d_{ff}=2048$ in paper.
:param d_input : Input dimension, default 512 in paper, which is the size of $d_{\rm model}$
:param d_hidden : Hidden dimenstion, default 2048 in paper.
"""
super(PositionWiseFeedForwardNetworks, self).__init__()
self.linear_1 = torch.nn.Linear(in_features=d_input, out_features=d_hidden)
self.linear_2 = torch.nn.Linear(in_features=d_hidden, out_features=d_input)
def forward(self, input: torch.FloatTensor) -> torch.FloatTensor:
"""
:param input : Shape is (*, `d_input`).
:return output : Shape is (*, `d_input`).
"""
x = self.linear_1(input)
x = torch.nn.ReLU()(x) # Relu(x) = max(0, x)
output = self.linear_2(x)
return output
01-16
- 临近回家综合征,啥事都做不成。唉… 这学期勉强算是逃过了周六的诅咒,却还是逃不过最终的亡语。
- 简单跑了五圈,权当休整了。
- PyTorch版本的Scaled Dot-Product Attention
class ScaledDotProductAttention(torch.nn.Module):
"""Section 3.2.1: Implementation for Scaled Dot-Product Attention"""
def __init__(self) -> None:
super(ScaledDotProductAttention, self).__init__()
def forward(self, q: torch.FloatTensor, k: torch.FloatTensor, v: torch.FloatTensor, mask: torch.LongTensor=None) -> (torch.FloatTensor, torch.FloatTensor):
"""
The Scaled Dot-Product Attention can be formulated as below:
$$
{\rm Attention}(Q, K, V) = {\rm softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V
$$
:param q : This is $Q$ above, whose shape is (batch_size, n_head, len_q, $d_q$)
:param k : This is $K$ above, whose shape is (batch_size, n_head, len_k, $d_k$)
:param v : This is $V$ above, whose shape is (batch_size, n_head, len_v, $d_v$)
:param mask : The value in `scores` will be replaced with 1e-9 if the corresponding value in mask, whose shape is (len_q, len_k), is 0.
Note:
- $d_q$ = $d_k$ holds and let $d_q$ = $d_k$ = d_output.
- `len_k = len_v` holds.
:return scores : (batch_size, n_head, len_q, len_k)
:return output : (batch_size, n_head, len_q, $d_v$)
"""
# batch_size: batch size of training input.
# n_head : The number of multi-heads.
# d_output : The dimension of $Q$, $K$, $V$.
d_q, d_k = q.shape[-1], k.shape[-1] # `d_k` is d_output.
assert d_q == d_k # Assumption: $d_q$ = $d_k$
scores = torch.matmul(q, k.transpose(2, 3)) / (d_k ** 0.5) # (batch_size, n_head, len_q, d_output) * (batch_size, n_head, d_output, len_k) -> (batch_size, n_head, len_q, len_k)
if mask is not None:
scores = scores.masked_fill(mask.unsqueeze(0).unsqueeze(0)==0, 1e-9)
scores = torch.nn.Softmax(dim=-1)(scores) # (batch_size, n_head, len_q, len_k) -> (batch_size, n_head, len_q, len_k)
output = torch.matmul(scores, v) # (batch_size, n_head, len_q, len_k) * (batch_size, n_head, len_k, $d_v$) -> (batch_size, n_head, len_q, $d_v$)
return output, scores
01-17
- 背了两台4kg的笔记本负重行军一小时,轻便与配置实在是不可兼得。也罢,愿明早一路顺风别堵车。
- PyTorch版本的Multi-head Attention
class MultiHeadAttention(torch.nn.Module):
"""Section 3.2.2: Implementation for Multi-Head Attention"""
def __init__(self, d_input: int, d_output: int, n_head: int) -> None:
"""
The Multi-Head Attention can be formulated as below:
$$
{\rm MultiHead}(Q, K, V) = {\rm Concat}({\rm head}_1, ... , {\rm head}_h)W^O \\
{\rm head}_i = {\rm Attention}(QW_i^Q, KW_i^K, VW_i^V)
$$
where:
- $W_i^Q \in \mathcal{R}^{d_{\rm model} × d_q}$
- $W_i^K \in \mathcal{R}^{d_{\rm model} × d_k}$
- $W_i^V \in \mathcal{R}^{d_{\rm model} × d_v}$
- $W^O \in \mathcal{R}^{hd_v × d_{\rm model}}$
- $h$ is the total number of heads.
- Note that $d_q = d_k$ holds.
- As is mentioned in paper, $h = 8$ and $d_k = d_v = \frac{d_{\rm model}}{h} = 64$ is set as default.
Below we set:
- `d_input` = $d_{\rm model}$
- `d_output` = $d_q$ = $d_k$ = $d_v$
- Usually, `d_input` = `d_output` is assumed so that residual connection is easy to calculate.
:param d_input : Input dimension of `MultiHeadAttention` module.
:param d_output : Output dimension of `MultiHeadAttention` module.
:param n_head : Total number of heads.
"""
super(MultiHeadAttention, self).__init__()
self.linear = torch.nn.Linear(in_features=n_head * d_output, out_features=d_input) # $W^O \in \mathcal{R}^{hd_v × d_{\rm model}}$
self.linear_q = torch.nn.Linear(in_features=d_input, out_features=n_head * d_output) # $W^Q \in \mathcal{R}^{d_{\rm model} × hd_q}$
self.linear_k = torch.nn.Linear(in_features=d_input, out_features=n_head * d_output) # $W^K \in \mathcal{R}^{d_{\rm model} × hd_k}$
self.linear_v = torch.nn.Linear(in_features=d_input, out_features=n_head * d_output) # $W^V \in \mathcal{R}^{d_{\rm model} × hd_v}$
self.n_head = n_head
self.d_output = d_output
self.scaled_dot_product_attention = ScaledDotProductAttention()
def forward(self, q: torch.FloatTensor, k: torch.FloatTensor, v: torch.FloatTensor, mask: torch.LongTensor=None) -> (torch.FloatTensor, torch.FloatTensor):
"""
$$
{\rm MultiHead}(Q, K, V) = {\rm Concat}({\rm head}_1, ... , {\rm head}_h)W^O \\
{\rm head}_i = {\rm Attention}(QW_i^Q, KW_i^K, VW_i^V)
$$
where:
- $d_q = d_k$ holds.
- `d_input` = $d_q$ = $d_k$ = $d_v$
:param q : This is $Q$ above, whose shape is (`batch_size`, `len_q`, $d_q$)
:param k : This is $K$ above, whose shape is (`batch_size`, `len_k`, $d_k$)
:param v : This is $V$ above, whose shape is (`batch_size`, `len_v`, $d_v$)
:param mask : The value in `scores` will be replaced with 1e-9 if the corresponding value in mask, whose shape is (len_q, len_k), is 0.
Note that `len_k` = `len_v` holds.
:return scores : (batch_size, n_head, len_q, len_k)
:return output : (batch_size, len_q, d_input)
"""
batch_size, len_q, len_k, len_v = q.shape[0], q.shape[1], k.shape[1], v.shape[1]
assert len_k == len_v # Assumption: seq_len = `len_k` = `len_v`
q = self.linear_q(q).contiguous().view(batch_size, len_q, self.n_head, self.d_output) # (batch_size, len_q, d_input) -> (batch_size, len_q, n_head * d_output) -> (batch_size, len_q, n_head, d_output)
k = self.linear_k(k).contiguous().view(batch_size, len_k, self.n_head, self.d_output) # (batch_size, len_k, d_input) -> (batch_size, len_k, n_head * d_output) -> (batch_size, len_k, n_head, d_output)
v = self.linear_v(v).contiguous().view(batch_size, len_v, self.n_head, self.d_output) # (batch_size, len_v, d_input) -> (batch_size, len_v, n_head * d_output) -> (batch_size, len_v, n_head, d_output)
q = q.transpose(1, 2) # (batch_size, len_q, n_head, d_output) -> (batch_size, n_head, len_q, d_output)
k = k.transpose(1, 2) # (batch_size, len_k, n_head, d_output) -> (batch_size, n_head, len_k, d_output)
v = v.transpose(1, 2) # (batch_size, len_v, n_head, d_output) -> (batch_size, n_head, len_v, d_output)
output, scores = self.scaled_dot_product_attention(q=q, k=k, v=v, mask=mask)# (batch_size, n_head, len_q, d_output), (batch_size, n_head, len_q, len_k)
output = output.transpose(1, 2).contiguous().view(batch_size, len_q, -1) # (batch_size, n_head, len_q, d_output) -> (batch_size, len_q, n_head, d_output) -> (batch_size, len_q, n_head * d_output)
output = self.linear(output) # (batch_size, len_q, n_head * d_output) -> (batch_size, len_q, d_input)
return output, scores # (batch_size, len_q, d_input), (batch_size, n_head, len_q, len_k)
01-18
- 养老期第一跑,选择路跑5.54km,配速4’42",看起来很一般,其实已经是在非常好的状态下的水平了。总之路跑确实挺难,上坡难跑,下坡难控制,这段时间可以好好练一练路跑,备战下半年的半马。
- 希望假期生活有规律吧,应该是难得比较清闲的一个假期了,养养老也挺好。
- PyTorch版本的Encoder
class Encoder(torch.nn.Module):
"""Section 3.1: Implementation for Encoder"""
def __init__(self, d_input: int, d_output: int, d_hidden: int, n_head: int, n_position: int) -> None:
"""
This is an implementation for one-time Encoder, which is repeated for six times in paper.
:param d_input : Input dimension of `Encoder` module.
:param d_output : Output dimension of `Encoder` module.
:param d_hidden : Hidden dimension of `PositionWiseFeedForwardNetworks` module.
:param n_head : Total number of heads.
:param n_position : Total number of position, that is the length of sequence.
"""
super(Encoder, self).__init__()
self.position_encoding = PositionalEncoding(d_input=d_input, d_output=d_output, n_position=n_position)
self.multi_head_attention = MultiHeadAttention(d_input=d_output, d_output=d_output, n_head=n_head)
self.layer_norm_1 = torch.nn.LayerNorm(d_output)
self.layer_norm_2 = torch.nn.LayerNorm(d_output)
self.position_wise_feed_forward_networks = PositionWiseFeedForwardNetworks(d_input=d_output, d_hidden=d_hidden)
def forward(self, input: torch.FloatTensor, mask: torch.LongTensor=None) -> torch.FloatTensor:
"""
See https://img-blog.csdnimg.cn/20210114103418782.png
:param input : Shape is (batch_size, `n_position`, `d_input`)
:param mask : Shape is (`n_position`, `n_position`)
:return output : Shape is (batch_size, `n_position`, `d_output`)
"""
q = self.position_encoding(input=input) # (*, n_position, d_input) -> (*, n_position, d_output)
k, v = q.clone(), q.clone() # $Q$, $K$, $V$ are just the same in Encoder, but it is a little different in Decoder.
residual_1 = q.clone() # `.clone()` is used for safety.
output_1, scores = self.multi_head_attention(q=q, k=k, v=v, mask=mask)
x = self.layer_norm_1(output_1 + residual_1) # Add & Norm: residual connection.
residual_2 = x.clone() # `.clone()` is used for safety.
output_2 = self.position_wise_feed_forward_networks(input=x) # Feed Forward
output = self.layer_norm_2(output_2 + residual_2) # Add & Norm: residual connection.
return output
01-19
- 路跑10km达成,配速4’45",最后基本是崩了,差点跑抽筋,是硬撑下来的。
- 相对来说冬天更倾向于不午睡,因为一旦上了床,就很难再下得来了,所以对夜晚睡眠时长与质量要求颇高,尽量做到早睡自然醒,才能保持住状态去跑更长的里程。
- 三天一篇paper,有灵感就写点代码,但愿寒假一个月能别太荒废罢。
- PyTorch版本的Decoder
class Decoder(torch.nn.Module):
"""Section 3.1: Implementation for Decoder"""
def __init__(self, d_input: int, d_output: int, d_hidden: int, n_head: int, n_position: int) -> None:
super(Decoder, self).__init__()
self.position_encoding = PositionalEncoding(d_input=d_input, d_output=d_output, n_position=n_position)
self.multi_head_attention_1 = MultiHeadAttention(d_input=d_output, d_output=d_output, n_head=n_head)
self.multi_head_attention_2 = MultiHeadAttention(d_input=d_output, d_output=d_output, n_head=n_head)
self.layer_norm_1 = torch.nn.LayerNorm(d_output)
self.layer_norm_2 = torch.nn.LayerNorm(d_output)
self.layer_norm_3 = torch.nn.LayerNorm(d_output)
self.position_wise_feed_forward_networks = PositionWiseFeedForwardNetworks(d_input=d_output, d_hidden=d_hidden)
def generate_subsequence_mask(self, subsequence):
"""
The subsequence mask is defined as a lower-triangle matrix with value 1.
"""
seq_len = subsequence.shape[1]
ones_tensor = torch.ones((seq_len, seq_len), dtype=torch.int, device=subsequence.device)
subsequence_mask = 1 - torch.triu(ones_tensor, diagonal=1) # Note that the value on diagonal is 1.
return subsequence_mask
def forward(self, encoder_output: torch.FloatTensor, target: torch.FloatTensor, mask: torch.LongTensor=None) -> torch.FloatTensor:
"""
See https://img-blog.csdnimg.cn/20210114103418782.png
:param encoder_output : Output of Encoder, whose shape is (batch_size, `n_position`, `d_output_encoder`)
:param target : Target tensor in dataset, whose shape is (batch_size, `n_position`, `d_input_decoder`)
:return output : Shape is (batch_size, `n_position`, `d_output`)
"""
q = self.position_encoding(input=target) # (*, n_position, d_input) -> (*, n_position, d_output)
k, v = q.clone(), q.clone() # $Q$, $K$, $V$ are just the same in Encoder, but it is a little different in Decoder.
residual_1 = q.clone() # `.clone()` is used for safety.
output_1, _ = self.multi_head_attention_1(q=q, k=k, v=v, mask=self.generate_subsequence_mask(target))
x = self.layer_norm_1(output_1 + residual_1) # Add & Norm: residual connection.
residual_2 = x.clone() # `.clone()` is used for safety.
output_2, _ = self.multi_head_attention_2(q=x, k=encoder_output, v=encoder_output, mask=mask)
x = self.layer_norm_2(output_2 + residual_2) # Add & Norm: residual connection.
residual_3 = x.clone() # `.clone()` is used for safety.
output_3 = self.position_wise_feed_forward_networks(input=x) # Feed Forward
output = self.layer_norm_3(output_3 + residual_3) # Add & Norm: residual connection.
return output
01-20
- 路跑7.12km,配速4’48",中途补了一个枣子,因为带水在身上实在是不太切实际,连续三天状态都还不错,果然在家吃得好是不一样。寒假的终极目标是路跑半马,而且我也已经想好了这条半马路线。
- ACL的论文里也有水平挺次的,感觉很多时候还是看学校和机构背景。
- PyTorch版本的Transformer
class Transformer(torch.nn.Module):
"""Attention is all you need: Implementation for Transformer"""
def __init__(self, d_input_encoder: int, d_input_decoder: int, d_output_encoder: int, d_output_decoder: int, d_output: int, d_hidden_encoder: int, d_hidden_decoder: int, n_head_encoder: int, n_head_decoder: int, n_position_encoder: int, n_position_decoder) -> None:
"""
:param d_input_encoder : Input dimension of Encoder.
:param d_input_decoder : Input dimension of Decoder.
:param d_output_encoder : Output dimension of Encoder.
:param d_output_decoder : Output dimension of Decoder.
:param d_output : Final output dimension of Transformer.
:param d_hidden_encoder : Hidden dimension of linear layer in Encoder.
:param d_hidden_decoder : Hidden dimension of linear layer in Decoder.
:param n_head_encoder=4 : Total number of heads in Encoder.
:param n_head_decoder=4 : Total number of heads in Decoder.
:param n_position_encoder : Sequence Length of Encoder Input, e.g. max padding length of Chinese sentences.
:param n_position_decoder : Sequence Length of Encoder Input, e.g. max padding length of English sentences.
"""
super(Transformer, self).__init__()
self.encoder = Encoder(d_input=d_input_encoder, d_output=d_output_encoder, d_hidden=d_hidden_encoder, n_head=n_head_encoder, n_position=n_position_encoder)
self.decoder = Decoder(d_input=d_input_decoder, d_output=d_output_decoder, d_hidden=d_hidden_decoder, n_head=n_head_decoder, n_position=n_position_decoder)
self.linear = torch.nn.Linear(in_features=d_output_decoder, out_features=d_output)
def forward(self, source, target) -> torch.FloatTensor:
"""
See https://img-blog.csdnimg.cn/20210114103418782.png
"""
encoder_output = self.encoder(source)
decoder_output = self.decoder(encoder_output, target)
x = self.linear(decoder_output)
output = torch.nn.Softmax(dim=-1)(x)
return output
def size(self):
size = sum([p.numel() for p in self.parameters()])
print('%.2fKB' % (size * 4 / 1024))
01-21
- 路跑6.17km,配速4’48",这次跑的是一个环线,其实还是留有余力的,可是眼前就是一个长上坡,还是就此而止了罢。
- 蓄力待时,我已经想好了一条15km的环线准备抽空去尝试,现在唯一的障碍是中途无法得到补给,以现在的水平零补给跑10km以上的里程难度很大。
- 寒假差不多在家一个月,争取月跑200km以上。
- 昨天看完paper之后开始研究python实现磁力链接下载的问题,发现前人也已经做了很多尝试,github上很多repository都有关于如何将磁力链接解析为种子文件(.torrent)的方法,但是基本上都是用了第三方工具(如aria2, libtorrent库)。
- 之所以开始想搞磁力链接,倒不是为了开车,主要还是不想再用迅雷了,新机上我甚至连微信都不装,因为我除了必要的软件之外,只想安装开源的软件(确切地说最好是portable的版本,像pdf阅读器sumatra直接下个zip解压就能用,都不会污染注册表),一来是确保不是流氓软件,二来是尽可能少地写入C盘。至少到目前为止,除了远程连接工具,压缩软件,浏览器,OFFICE全家桶外,其他的音像播放器(potplayer),文本编辑器(notepad++ sumatra)都是开源的。
- 这里我正好推荐一个神器网站FOSSHUB,这上面所有软件都是开源的,绝无绑定和广告,而且一定都是足够精简的。部分还是portable的,sumutra就在上面,我昨天下了一个portable的备份软件,才几个4Mb大小,源码才几百k,真是相见恨晚。自从WIN10升级后,连联想自带的备份软件联想一键恢复都无法备份当前版本的系统了。
- 回到磁力链接的问题上,确实目前国内还是迅雷一家独大,而且因为磁力链接本身的特性,导致用户基数巨大的迅雷实然是最好的选择,但是我肯定是不可能给新机装迅雷的,那就必须自己解决了。首先我是先把多进程和多线程下载文件的python脚本写了一下,速度还不错,有空可以分享一下,然后就开始四处搜寻磁力链接下载的方法,事实上因为libtorrent不开源之后,python-libtorrent库的源码也无法下载了,现在连从磁力链接(40位的SHA码)解析出种子文件(.torrent)都极其困难(其实用迅雷偶尔也会难以解析很老的磁力链接,本身我理解解析磁力链接就是求哈希函数的逆,这从哈希函数的定义上来说就是难以求逆的,我挺好奇这个具体原理是怎么样的,难道就是穷举?迅雷可能是已经有足够大的种子文件库,可能直接去比对就能解析出种子文件了)。然后就是怎么连接tracker服务器。
- 关于具体了解磁力链接我推荐一篇英文blog:https://markuseliasson.se/article/bittorrent-in-python/,非常详细,其实原作者本身尝试写了一个磁力链接下载器的python脚本(在原文链接中有),我大致看了一下,因为他自己说还很不完善,我也没有深究,后来我是参考了GitHub@magnet-dht,作者也是同道中人了,按照README里的说法已经可以实现到下载了,至于解析磁力链接,他用的是aria2,可惜跟libtorrent一样,都是C++编译的,很难装… 我也没看懂他里面到底是怎么用aria2的。
- 四处碰壁后我去FOSSHUB上找了qBittorrent,在旧机上先测试了一下,算是比较简约的软件,评价也很好,但是用起来效果很一般,老旧的磁力链接还是下不下来,不过我倒是用它把http://amvnews.ru/index.php?go=Files&in=view&id=4470上的U神的AMV神作Our Tapes(中文名就是著名的秋山澪与折木奉太郎的爱情故事,B站有转载https://www.bilibili.com/video/BV1nx411F7Jf)给下载到本地,留作一个高清版本作为收藏。
- 总之我挺希望有大神能写出一个非常好用的开源磁力链接下载器,再不断推广,至少可以在Github这种社区里通用,让我们能享受资源快速共享,因为很多国外下载链接都很慢(包括git下载的速度),如果能都用上磁力链接,实在是再好不过了,哪怕只是局限在码农这个群体中,分享一些数据,exe,源码等等,现在回看像pandownload(基于aria2开发),SimDTU,这些GitHub项目都已经挂掉了,libtorrent都不开源了,不禁让我们这些后来的人唏嘘不已,更多时候还是得靠自己才行了唉。
01-22
- 第一次看复联,刷了美队三部,我的老天爷,堕落的生活又开始了,实话说还真挺好看。
- 昨天有个叫周红喜的人加我vx,我也不知道是谁,也只好接受了,然后上来他问我“贵姓,男生女生?”我就很纳闷,于是就晾着他,过了四五个小时又问“男孩?女生?”,我还是晾着他,感觉不是个好东西,我就想看看这家伙能有啥事,我也不问他是谁,找我干嘛,反正我一个山野闲人能有啥好事,你没事我也没事呗~
- 雨天,跑步机伺候,5分配的10km,尚有余力,感觉至少能再坚持10分钟以上,目前的极限是跨年那晚的4’44"配速下的场地跑15.2km,感觉在跑步机上是可以达到半马水平的了。
- 记录今天搞路由器和网关(猫)的问题:其实我对这块还真是一窍不通;
- 前几天连有线,把网关千兆口上原先连在路由器WAN口上的网线拔了,换了有线的网线连到笔记本,速度一流,然后把WAN口的网线绑到百兆口上,结果从此家里就没有WIFI了,原来百兆口只能给机顶盒用,且非中国电信天翼超级用户,是不能把百兆口改成可移动端连网的。
- 后来把网关千兆口和百兆口的线对调,WIFI能上了,有线又不行了。
- 最后知道是把有线要连在路由器的LAN口(一般有4个,WAN口只有1个)上才能联网,原因是WAN口是连外网,LAN口是连内网,有线算内网。
- 网关的用户名(一般是useradmin)和密码在猫盒背面,访问192.168.1.1一般可以登陆进行管理,我今天才发现不知道是哪个缺德的在背面贴了个条形码,刚好把密码给挡住了,我小刀刮了半天才勉强看清楚密码。。。
01-23
- 又刷了四部复联,心满意足,老美拍超级英雄确实有一手。
- 雨天跑步机10km,左髋有点疼,应该问题不大。
- 拓扑排序python脚本
def toposort(graph):
in_degrees = dict((u,0) for u in graph) #初始化所有顶点入度为0
vertex_num = len(in_degrees)
for u in graph:
for v in graph[u]:
in_degrees[v] += 1 #计算每个顶点的入度
Q = [u for u in in_degrees if in_degrees[u] == 0] # 筛选入度为0的顶点
Seq = []
while Q:
u = Q.pop() #默认从最后一个删除
Seq.append(u)
for v in graph[u]:
in_degrees[v] -= 1 #移除其所有指向
if in_degrees[v] == 0:
Q.append(v) #再次筛选入度为0的顶点
if len(Seq) == vertex_num: #如果循环结束后存在非0入度的顶点说明图中有环,不存在拓扑排序
return Seq
else:
print("there's a circle.")
01-24
- 路跑了一次4km速耐,明显感觉不如场地跑,任重道远。第一周52km多一些,勉强说得过去。
- 旧机搞崩了,真的是手贱,现在准备重装系统,过去的东西都不要了,Adobe全家桶近三年都没打开过,丢了就丢了吧,准备之后只装微信和迅雷,因为这两个不打算再在新机上装。推荐一个图片查看器https://www.fosshub.com/FastStone-Image-Viewer.html,用下来还不错,比WIN10自带的好多了。
- 关于python的异步代码(我还真是第一次看到可以在
def前面加async,这玩意儿Python 3.5的时候就有了)
import asyncio
from random import randint
async def do_stuff(ip, port):
print('About to open a connection to {ip}'.format(ip=ip))
reader, writer = await asyncio.open_connection(ip, port)
print('Connection open to {ip}'.format(ip=ip))
await asyncio.sleep(randint(0, 5))
writer.close()
print('Closed connection to {ip}'.format(ip=ip))
if __name__ == '__main__':
loop = asyncio.get_event_loop()
work = [
asyncio.ensure_future(do_stuff('8.8.8.8', '53')),
asyncio.ensure_future(do_stuff('8.8.4.4', '53')),
]
loop.run_until_complete(asyncio.gather(*work))
01-25
- 出门暴饮暴食,回来跑步机10km,事实上跑得不是很尽兴,有余力,感能上20km的感觉,可惜时间不够了。果然多吃一些是不一样的。
- 新手上路,一天吃一个罚单,烦得很,开得没自信了。
- 使用
datetime.datetime.fromtimestamp():
- 代码示例:
from datetime import datetime timestamp = 1381419600 print(datetime.fromtimestamp(timestamp))- 输出结果:
2013-10-10 23:40:00
- 输出结果:
- 注意:
- 该函数无keyword augments, 即不需要添加参数名称;
- 与
time.localtime()函数不同,datetime.datetime.fromtimestamp()接收的时间戳至少为86400, 前者则可以从0开始;
01-26
- 研究了一天aria2,发现好东西是不配给草包用的。
- 重置了老电脑,发现速度倒还可以,果然之前还是装的东西太多了,准备花一段时间好好整顿一下。
- 试了一下跑步机12km,还是没啥压力,等天气好了再去路跑。
- 关于WIN10下aria2的使用:这玩意儿支持磁力链接和种子下载,以及各种传统下载方式,可以替代迅雷那垃圾玩意儿。参考自http://www.360doc.com/content/19/0830/16/20268466_858072587.shtml
- 下载aria2的源码:https://github.com/aria2/aria2/releases
- 下载aria2的GUI(有个GUI总归好,要不然终端里指令太多真的记不住):https://github.com/mayswind/AriaNg/releases
- 注意这个AriaNg是一个网页版的GUI,界面还不错

- 下载前人写好的配置文件:https://cdn.51shenyun.cn/Aria2_Win_config.zip
- 最后把这三个玩意儿解压后的内容塞到同一个目录下即可

- 原文作者给了个懒人包:https://cdn.51shenyun.cn/Aria2_Win.zip
- 这玩意儿下下来解压就能用,缺陷是不是最新版本的aria2,不过好处是原文作者把中文包编译进去了,所以下载的GUI界面是中文的比较友好。我下的最新版本调了半天GUI都是英文的,没找到怎么改语言。
- 注意这个AriaNg是一个网页版的GUI,界面还不错
01-27
- 路跑15.21km,选的是一条大环线,挺极限的了,一口气跑完,中途有几处爬坡,终点500米冲刺,很久没有这种畅快了。
- 这两天装机接触到很多有趣的东西,比如油猴(TamperMonkey)下的许多用户脚本,Motric下载器,ariac2,感叹前人真的为资源共享做出太多贡献,为了攻破百度云盘的防御,一代又一代的码工在前赴后继的写脚本,可惜现在真的连aria2也不管用了,被迫安装了百度云客户端,真的是屈辱至极。
- BT下载Tracker服务器爬取:由衷感谢开源贡献者们的工作
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
import re
import requests
from bs4 import BeautifulSoup
class Tracker(object):
def __init__(self) -> None:
self.mirrors_all = [
'https://trackerslist.com/all.txt'
'https://cdn.jsdelivr.net/gh/XIU2/TrackersListCollection@master/all.txt',
'http://github.itzmx.com/1265578519/OpenTracker/master/tracker.txt',
]
self.mirrors_best = [
'https://trackerslist.com/best.txt',
'https://cdn.jsdelivr.net/gh/XIU2/TrackersListCollection@master/best.txt',
]
self.mirrors_bestip = [
'https://cdn.jsdelivr.net/gh/ngosang/trackerslist@master/trackers_best_ip.txt',
]
self.mirrors_http = [
'https://trackerslist.com/http.txt',
'https://cdn.jsdelivr.net/gh/XIU2/TrackersListCollection@master/http.txt',
]
self.mirrors_https = [
'https://cdn.jsdelivr.net/gh/ngosang/trackerslist/trackers_all_https.txt',
]
self.mirrors_ws = [
'https://cdn.jsdelivr.net/gh/ngosang/trackerslist/trackers_all_ws.txt',
]
self.mirrors_udp = [
'https://cdn.jsdelivr.net/gh/ngosang/trackerslist/trackers_all_udp.txt',
]
self.mirrors_ip = [
'https://cdn.jsdelivr.net/gh/ngosang/trackerslist@master/trackers_all_ip.txt'
]
self.mirrors_blacklist = [
'https://cdn.jsdelivr.net/gh/ngosang/trackerslist@master/blacklist.txt',
]
self.mirrors = {
'all': self.mirrors_all,
'best': self.mirrors_best,
'bestip': self.mirrors_bestip,
'http': self.mirrors_http,
'https': self.mirrors_https,
'ws': self.mirrors_ws,
'udp': self.mirrors_udp,
'ip': self.mirrors_ip,
}
self.label_compiler = re.compile(r'<[^>]+>', re.S)
def get_trackers(self, category: str='best', filter_blacklist=False) -> list:
def _parse(html):
soup = BeautifulSoup(html, 'lxml')
body_html = str(soup.find('body').string)
trackers = self.label_compiler.sub('', body_html).split()
return trackers
mirrors = self.mirrors.get(category)
assert category is not None
flag = False
for mirror in mirrors:
try:
print('Try mirror: {} ...'.format(mirror))
response = requests.get(mirror)
flag = True
break
except:
print(' - Fail ...')
continue
if not flag:
print('All {} mirrors for trackers are fail.'.format(category))
return []
html = response.text
trackers = _parse(html)
if filter_blacklist:
print('Fetch blacklist ...')
flag = False
for mirror in self.mirrors_blacklist:
try:
print('Try mirror: {} ...'.format(mirror))
response = requests.get(mirror)
flag = True
break
except:
print(' - Fail ...')
continue
if not flag:
print('Fail to fetch blacklist.')
blacklist = []
else:
html = response.text
blacklist = _parse(html)
for tracker in trackers[:]:
if tracker in blacklist:
trackers.remove(tracker)
return trackers
if __name__ == '__main__':
t = Tracker()
trackers = t.get_trackers()
from pprint import pprint
pprint(trackers)
print(','.join(trackers))
01-28
- 4’33"配4km,休息一分多钟后4’47"配3.17km,感觉路跑的速耐很难,因为有很多爬坡要上,现在的水平还很难跑进4’30",目前场地pb是3km 12’58",6km 26’38",10km 45’53",15km 71’08",配速分别是4’19",4’25",4’35",4’45"
- 装了matlab,因为忽然想起要补优化理论,到时候作业肯定得要,现在R2020a装完占了30多G,实在是太离谱了。
- 之前搞IDEA也费了很大事,最后选了别人一个装好的portable的版本,2019.3版本的,勉强凑合,主要还是不太想丢掉Java,虽然以后可能用的很少。
- aria2:开源下载器中的巅峰之作
aria2c [资源链接URL]aria2c [40位的种子哈希]aria2c [.torrent文件路径]- 几个以aria2为基础,做成GUI界面的下载器:Motric(强推),PanDownload(虽然全网封禁,但是也是aria2的辉煌),IDM(这玩意儿似乎要破解,比较麻烦,虽然挺好),qBittorrent和比特彗星。
01-29
- 路跑第12天,状态低迷,左右肩和左右大腿都疼得不行,慢跑4km就废了,休息完回程又跑了4km多一些,精疲力竭。前天强行15km一时爽,可能又要废一阵子了。目前这周5天的历程分别是:10km(跑步机) 12km(跑步机)15.21km(路跑)7.17km(间歇)8.5km,已经达到日均10km以上的跑量了。
- 解析磁链很难,最终还是屈服于迅雷,虽然吸血雷,但是耐不住快,是香…
- Tensorflow自定义层:
# -*- coding: UTF-8 -*-
import os
import gc
import re
import time
import keras
import numpy as np
import pandas as pd
from tqdm import tqdm
import tensorflow as tf
import keras.backend as K
from keras.layers import *
from keras.models import *
from sklearn import metrics
from keras.callbacks import *
from keras.optimizers import *
from unidecode import unidecode
from keras.initializers import *
from keras.preprocessing.text import Tokenizer
from keras.losses import categorical_crossentropy
from keras.preprocessing.sequence import pad_sequences
from keras_bert import load_trained_model_from_checkpoint
from sklearn.model_selection import train_test_split,StratifiedKFold
from keras import initializers,regularizers,constraints,optimizers,layers
class MyLayer(Layer):
def __init__(self, output_dim, **kwargs):
self.output_dim = output_dim
super(MyLayer, self).__init__(**kwargs)
def build(self, input_shape):
# Create a trainable weight variable for this layer.
self.kernel = self.add_weight(name='kernel',
shape=(input_shape[1], self.output_dim),
initializer='uniform',
trainable=True)
super(MyLayer, self).build(input_shape) # Be sure to call this somewhere!
def call(self, x):
return K.dot(x, self.kernel)
def compute_output_shape(self, input_shape):
return (input_shape[0], self.output_dim)
def model_1(
max_features=32768, # 单词种类数
embed_size=256, # 词向量维度
d_input=(100,), # 原始句向量形状(#token,#emb)
d_output=(100,), # 目标句向量形状(#token,#emb)
dropout=0.12, # 残差连接概率
lr=0.008, # 学习率(步长)
is_summarized=True, # 是否输出网络概况
):
K.clear_session()
input_tensor = Input(shape=d_input)
x = Embedding(max_features,embed_size,mask_zero=False,trainable=False,input_length=d_input[0])(input_tensor)
x = Flatten()(x)
x = MyLayer(25600)(x)
x = Dense(128,activation="relu")(x)
model = Model(inputs=input_tensor,outputs=x)
if is_summarized: model.summary()
return model
if __name__ == "__main__":
model = model_1()
01-30
- 休整一日,连续12天日均8km以上的跑量,腿实在是挺不住了(主要是27日的15km路跑太伤了)。医生朋友提醒我跑步对膝盖损伤极大,现在不注意,年纪大了肯定会有后遗症的。
- 油猴其实一般,我感觉那些脚本我也写过不少,只是油猴的用户脚本基本上都是内嵌浏览器的javascript脚本,用起来方便一些,但是无效的方法也很多,比如之前破不了QQ音乐的下载,油猴也拿它没办法,而且现在所有百度云盘直链下载的脚本都挂了,不过倒是看到不少视频网站的脚本,有空试试视频的下载,有些好mv还是很值得收藏的。
- opencv的一些脚本(其实这个库还能操控计算机的摄像头,还是挺有意思的):
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: CaoYang@163.sufe.edu.cn
import numpy as np
import cv2
'''
定义裁剪函数, 四个参数分别是:
左上角横坐标x0
左上角纵坐标y0
裁剪宽度w
裁剪高度h
'''
crop_image = lambda img,x0,y0,w,h: img[y0:y0+h,x0:x0+w]
'''
随机裁剪
area_ratio为裁剪画面占原画面的比例
hw_vari是扰动占原高宽比的比例范围
'''
def random_crop(img,area_ratio,hw_vari):
h,w = img.shape[:2]
hw_delta = np.random.uniform(-hw_vari,hw_vari)
hw_mult = 1 + hw_delta
# 下标进行裁剪, 宽高必须是正整数
w_crop = int(round(w*np.sqrt(area_ratio*hw_mult)))
# 裁剪宽度不可超过原图可裁剪宽度
if w_crop > w:
w_crop = w
h_crop = int(round(h*np.sqrt(area_ratio/hw_mult)))
if h_crop > h:
h_crop = h
# 随机生成左上角的位置
x0 = np.random.randint(0,w-w_crop+1)
y0 = np.random.randint(0,h-h_crop+1)
return crop_image(img,x0,y0,w_crop,h_crop)
'''
定义旋转函数:
angle是逆时针旋转的角度
crop是个布尔值, 表明是否要裁剪去除黑边
'''
def rotate_image(img,angle,crop):
h,w = img.shape[:2]
# 旋转角度的周期是360°
angle %= 360
# 用OpenCV内置函数计算仿射矩阵
M_rotate = cv2.getRotationMatrix2D((w/2,h/2),angle,1)
# 得到旋转后的图像
img_rotated = cv2.warpAffine(img,M_rotate,(w,h))
# 如果需要裁剪去除黑边
if crop:
# 对于裁剪角度的等效周期是180°
angle_crop = angle % 180
# 并且关于90°对称
if angle_crop > 90:
angle_crop = 180 - angle_crop
# 转化角度为弧度
theta = angle_crop * np.pi / 180.0
# 计算高宽比
hw_ratio = float(h) / float(w)
# 计算裁剪边长系数的分子项
tan_theta = np.tan(theta)
numerator = np.cos(theta) + np.sin(theta) * tan_theta
# 计算分母项中和宽高比相关的项
r = hw_ratio if h > w else 1 / hw_ratio
# 计算分母项
denominator = r * tan_theta + 1
# 计算最终的边长系数
crop_mult = numerator / denominator
# 得到裁剪区域
w_crop = int(round(crop_mult*w))
h_crop = int(round(crop_mult*h))
x0 = int((w-w_crop)/2)
y0 = int((h-h_crop)/2)
img_rotated = crop_image(img_rotated,x0,y0,w_crop,h_crop)
return img_rotated
'''
随机旋转
angle_vari是旋转角度的范围[-angle_vari,angle_vari)
p_crop是要进行去黑边裁剪的比例
'''
def random_rotate(img,angle_vari,p_crop):
angle = np.random.uniform(-angle_vari,angle_vari)
crop = False if np.random.random() > p_crop else True
return rotate_image(img,angle,crop)
'''
定义hsv变换函数:
hue_delta是色调变化比例
sat_delta是饱和度变化比例
val_delta是明度变化比例
'''
def hsv_transform(img,hue_delta,sat_mult,val_mult):
img_hsv = cv2.cvtColor(img,cv2.COLOR_BGR2HSV).astype(np.float)
img_hsv[:,:,0] = (img_hsv[:,:,0] + hue_delta) % 180
img_hsv[:,:,1] *= sat_mult
img_hsv[:,:,2] *= val_mult
img_hsv[img_hsv > 255] = 255
return cv2.cvtColor(np.round(img_hsv).astype(np.uint8),cv2.COLOR_HSV2BGR)
'''
随机hsv变换
hue_vari是色调变化比例的范围
sat_vari是饱和度变化比例的范围
val_vari是明度变化比例的范围
'''
def random_hsv_transform(img,hue_vari,sat_vari,val_vari):
hue_delta = np.random.randint(-hue_vari,hue_vari)
sat_mult = 1 + np.random.uniform(-sat_vari,sat_vari)
val_mult = 1 + np.random.uniform(-val_vari,val_vari)
return hsv_transform(img,hue_delta,sat_mult,val_mult)
'''
定义gamma变换函数:
gamma就是Gamma
'''
def gamma_transform(img,gamma):
gamma_table = [np.power(x / 255.0,gamma) * 255.0 for x in range(256)]
gamma_table = np.round(np.array(gamma_table)).astype(np.uint8)
return cv2.LUT(img,gamma_table)
'''
随机gamma变换
gamma_vari是Gamma变化的范围[1/gamma_vari,gamma_vari)
'''
def random_gamma_transform(img,gamma_vari):
log_gamma_vari = np.log(gamma_vari)
alpha = np.random.uniform(-log_gamma_vari,log_gamma_vari)
gamma = np.exp(alpha)
return gamma_transform(img,gamma)
01-31
- 早上起床发现左膝盖疼我就知道事情不太对了,又给老妈抓住把柄了,这几天先在跑步机上休整了,确实是伤了。
- 最近补了不少番和剧,这两天迷上了逆转裁判,本来是部游戏,但是改编的番剧情不太全,在B站上找了个全程实况的云通关了一下,确实剧情挺不错的,算是推理游戏中做得相当好的video game了。
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: lzwcy110@163.com
import json
import requests
from urllib.parse import urlencode
from datetime import datetime,timedelta
from baiduindex_utils import *
from baiduindex_config import *
class Index(object):
def __init__(self,keywords,start_date,end_date,cookies,area=0):
# 1. 参数校验
print("正在检查参数可行性...")
assert is_cookies_valid(cookies),"cookies不可用!" # 检查cookie是否可用
print(" - cookies检测可用!")
assert is_keywords_valid(keywords),"keywords集合不合规范!" # 检查keywords集合是否符合规范
print(" - keywords集合符合规范!")
print(" - 检查每个keyword是否存在可查询的指数...")
for i in range(len(keywords)): # 检查每个keyword是否有效
for j in range(len(keywords[i])):
flag = is_keyword_existed(keywords[i][j],cookies)
print(" + 关键词'{}'有效性: {}".format(keywords[i][j],flag))
if not flag: keywords[i][j] = str() # 置空无效关键词
keywords = list(filter(None,map(lambda x: list(filter(None,x)),keywords))) # 删除无效关键词与无效关键词组
print(" - 删除无效关键词后的keywords集合: {}".format(keywords))
assert days_duration(start_date,end_date)+1<=MAX_DATE_LENGTH,"start_date与end_date间隔不在可行范围内: 0~{}".format(MAX_DATE_LENGTH)
print(" - 日期间隔符合规范!")
assert int(area)==0 or int(area) in CODE2PROVINCE,"未知的area!" # 检查area是否在CODE2PROVINCE中, 0为全国
print(" - area编号可以查询!")
print("参数校验通过!")
# 2. 类构造参数
self.keywords = keywords # 关键词: 二维列表: [["拳皇","街霸"],["英雄联盟","绝地求生"],["围棋","象棋"]]
self.start_date = start_date # 起始日期: yyyy-MM-dd
self.end_date = end_date # 终止日期: yyyy-MM-dd
self.cookies = cookies # cookie信息
self.area = area # 地区编号: 整型数, 默认值全国(0)
# 3. 类常用参数
self.index_names = ["search","news","feedsearch"] # 被加密的三种指数: 搜索指数, 媒体指数, 资讯指数
def get_decrypt_key(self,uniqid): # 根据uniqid请求获得解密密钥
response = request_with_cookies(API_BAIDU_INDEX_KEY(uniqid),self.cookies)
json_response = json.loads(response.text)
decrypt_key = json_response["data"]
return decrypt_key
def get_encrypt_data(self,api_name="search"): # 三个API接口(搜索指数, 媒体指数, 资讯指数)获取加密响应的方式: api_name取值范围{"search","news","feedsearch"}
word_list = [[{"name":keyword,"wordType":1} for keyword in group] for group in self.keywords]
assert api_name in self.index_names,"Expect param 'api_name' in {} but got {} .".format(self.index_names,api_name)
if api_name=="search": # 搜索指数相关参数
field_name = "userIndexes"
api = API_SEARCH_INDEX
kwargs = KWARGS_SEARCH_INDEX
if api_name=="news": # 媒体指数相关参数
field_name = "index"
api = API_NEWS_INDEX
kwargs = KWARGS_NEWS_INDEX
if api_name=="feedsearch": # 资讯指数相关参数
field_name = "index"
api = API_FEEDSEARCH_INDEX
kwargs = KWARGS_FEEDSEARCH_INDEX
query_string = kwargs.copy()
query_string["word"] = json.dumps(word_list)
query_string["startDate"] = self.start_date
query_string["endDate"] = self.end_date
query_string["area"] = self.area
query_string = urlencode(query_string)
response = request_with_cookies(api(query_string),self.cookies)
json_response = json.loads(response.text)
uniqid = json_response["data"]["uniqid"]
encrypt_data = []
for data in json_response["data"][field_name]: encrypt_data.append(data)
return encrypt_data,uniqid
def get_index(self,index_name="search"): # 获取三大指数: 搜索指数, 媒体指数, 资讯指数
index_name = index_name.lower().strip()
assert index_name in self.index_names,"Expect param 'index_name' in {} but got {} .".format(self.index_names,index_name)
encrypt_data,uniqid = self.get_encrypt_data(api_name=index_name)# 获取加密数据与密钥请求参数
decrypt_key = self.get_decrypt_key(uniqid) # 获取解密密钥
if index_name=="search": # 搜索指数区别于媒体指数与资讯指数, 搜索指数分是分SEARCH_MODE的
for data in encrypt_data: # 遍历每个数据
for mode in SEARCH_MODE: # 遍历所有搜索方式解密: ["all","pc","wise"]
data[mode]["data"] = decrypt_index(decrypt_key,data[mode]["data"])
keyword = str(data["word"])
for mode in SEARCH_MODE: # 遍历所有搜索方式格式化: ["all","pc","wise"]
_start_date = datetime.strptime(data[mode]["startDate"],"%Y-%m-%d")
_end_date = datetime.strptime(data[mode]["endDate"],"%Y-%m-%d")
dates = [] # _start_date到_end_date(包头包尾)的日期列表
while _start_date<=_end_date: # 遍历_start_date到_end_date所有日期
dates.append(_start_date)
_start_date += timedelta(days=1)
index_list = data[mode]["data"]
if len(index_list)==len(dates): print("指数数据长度与日期长度相同!")
else: print("警告: 指数数据长度与日期长度不一致, 指数一共有{}个, 日期一共有{}个, 可能是因为日期跨度太大!".format(len(index_list),len(dates)))
for i in range(len(dates)): # 遍历所有日期
try: index_data = index_list[i] # 存在可能日期数跟index数匹配不上的情况
except IndexError: index_data = "" # 如果意外匹配不上就置空好了
output_data = {
"keyword": [keyword_info["name"] for keyword_info in json.loads(keyword.replace("'",'"'))],
"type": mode, # 标注是哪种设备的搜索指数
"date": dates[i].strftime('%Y-%m-%d'),
"index": index_data if index_data else "0", # 指数信息
}
yield output_data
if index_name in ["news","feedsearch"]:
for data in encrypt_data:
data["data"] = decrypt_index(decrypt_key,data["data"]) # 将data字段替换成解密后的结果
keyword = str(data["key"])
_start_date = datetime.strptime(data["startDate"],"%Y-%m-%d")
_end_date = datetime.strptime(data["endDate"],"%Y-%m-%d")
dates = [] # _start_date到_end_date(包头包尾)的日期列表
while _start_date<=_end_date: # 遍历_start_date到_end_date所有日期
dates.append(_start_date)
_start_date += timedelta(days=1)
index_list = data["data"]
if len(index_list)==len(dates): print("指数数据长度与日期长度相同!")
else: print("警告: 指数数据长度与日期长度不一致, 指数一共有{}个, 日期一共有{}个, 可能是因为日期跨度太大!".format(len(index_list),len(dates)))
for i in range(len(dates)): # 遍历所有日期
try: index_data = index_list[i] # 存在可能日期数跟index数匹配不上的情况
except IndexError: index_data = "" # 如果意外匹配不上就置空好了
output_data = {
"keyword": [keyword_info["name"] for keyword_info in json.loads(keyword.replace("'",'"'))],
"date": dates[i].strftime('%Y-%m-%d'),
"index": index_data if index_data else "0", # 没有指数对应默认为0
}
yield output_data
if __name__ == "__main__":
pass
2021年2月
02-01
- 跑步机12km,状态不是很行,跑完已经崩溃了,毕竟休整了两天,一下子上这种量不是很明智。现在全家都抵制我跑步,就怕我以后腿残走不了路,烦的很。
- 逆转裁判看到复苏的逆转,录播全长有将近800分钟,非常精彩的剧情,没想到video game也能做出让人身临其境的效果,不得不说脚本作者太强了,这可比写一本悬疑小说难多了(得构思好多支线)。
- 最近的确没做啥事,简单分享一个python的装饰器
numba,可以用来提高代码运行效率,不过看到最近十几天虽然没有写东西,还是有几位小伙伴关注了我,等我看完逆转裁判一定好好学习… [Facepalm]
- 有兴趣的可以试试,这玩意儿好像还有点用处:
from numba import jit
import random
import time
@jit(nopython=True)
def monte_carlo_pi(nsamples):
acc = 0
for i in range(nsamples):
x = random.random()
y = random.random()
if (x*x+y*y)<1.0: acc += 1
return 4.0*acc/nsamples
@numba.jit(nopython=True,parallel=True)
def logistic_regression(Y,X,w,iterations):
for i in range(iterations):
w -= np.dot(((1.0/(1.0+np.exp(-Y*np.dot(X,w)))-1.0)*Y),X)
return w
def logistic_regression_(Y,X,w,iterations):
for i in range(iterations):
w -= np.dot(((1.0/(1.0+np.exp(-Y*np.dot(X,w)))-1.0)*Y),X)
return w
02-02
- 禁足令
- 闲来无事试了一下b站视频下载,目前倒是可行的,简单说一下方法:
- 到视频页后刷新监听XHR下面的MP4文件
- 这里有个小问题,就是并非所有视频都可以监听到mp4文件,有些可能是m4s,有些可能是flv,如果类型那栏看不太出来就去看看文件那栏,总会有文件格式信息的,或者直接筛选媒体而非XHR
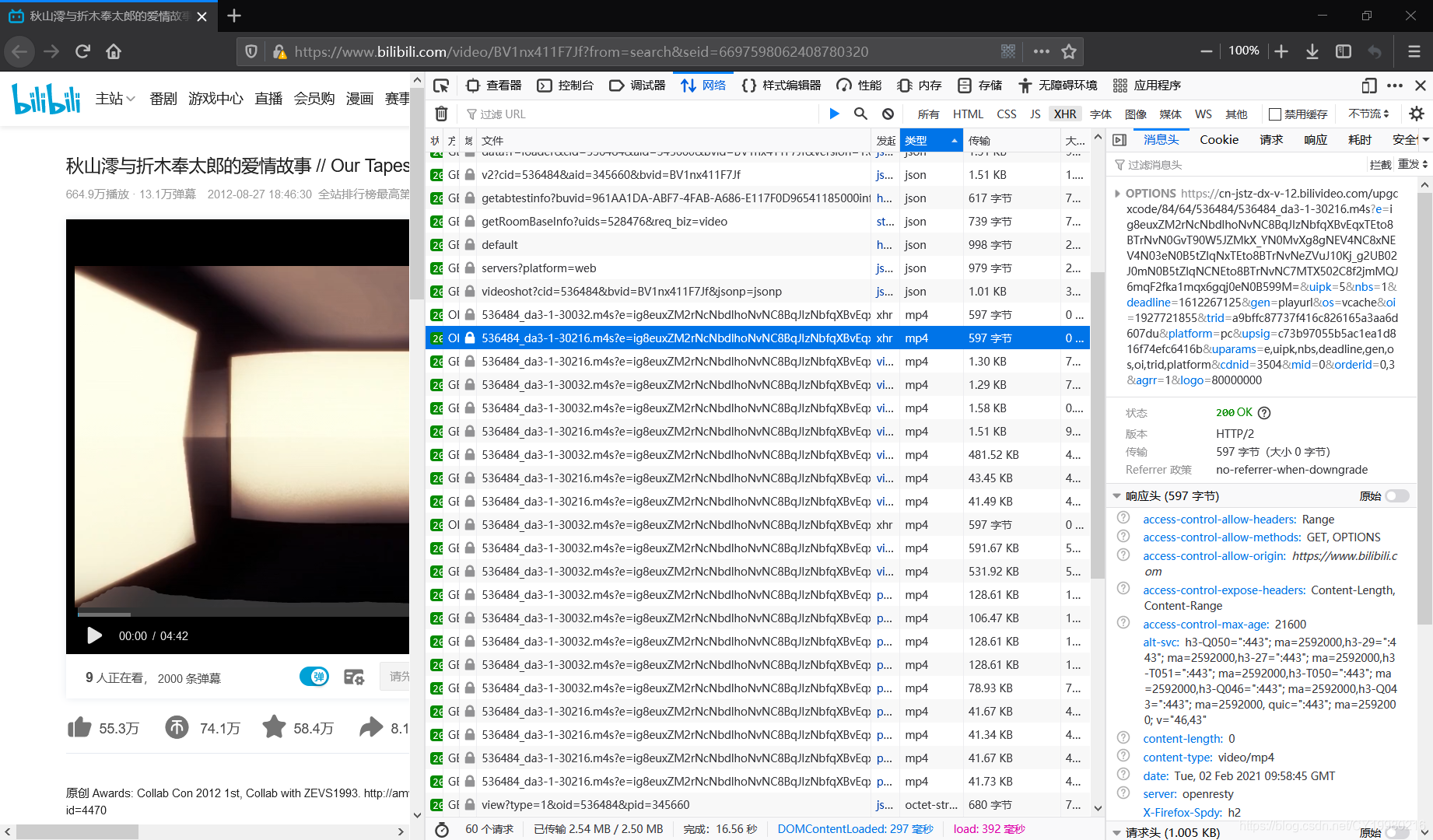
- 这里有个小问题,就是并非所有视频都可以监听到mp4文件,有些可能是m4s,有些可能是flv,如果类型那栏看不太出来就去看看文件那栏,总会有文件格式信息的,或者直接筛选媒体而非XHR
- 随意拉开一个看看响应头(为什么会有很多?因为视频总是分块传回前端,否则太大了…)
- 注意看到下图中蓝色标识出来的content-range: bytes 933-1648/2375632,这意味着这个响应数据流一共有2375632字节,该请求是933-1648字节这块。所以其实只要改成content-range: bytes 933-2375632/2375632就可以得到完整的视频了。
- 关于2375632的位置一般来说包含在响应头里的一个content-length字段中,不过这里没有,我看了一些其他的可能是会有的,这东西并不严格。
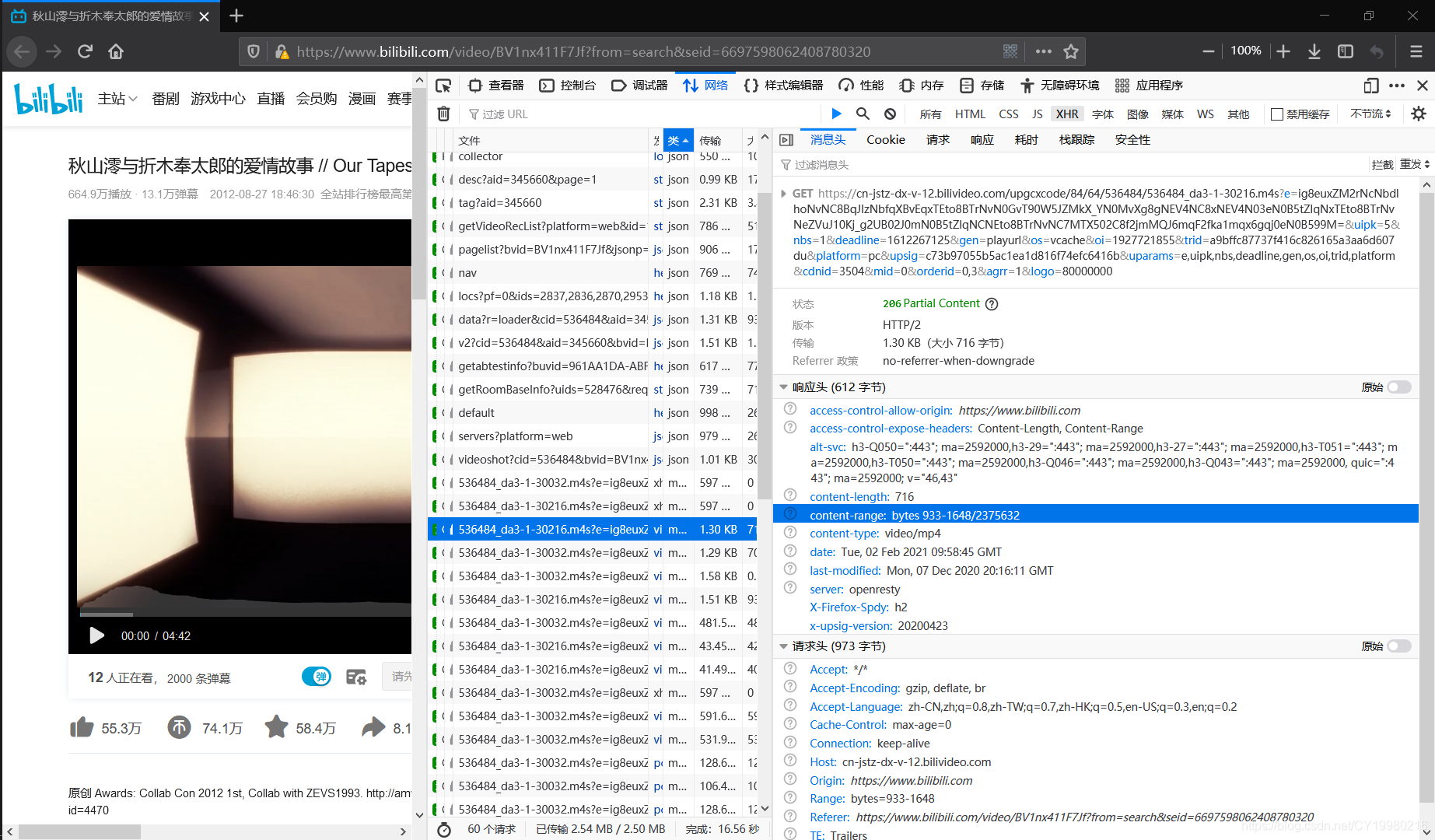
- 直接邮件重新编辑发送即可,按照我刚才说的改请求头发送一次即可👇

- 一些细节就不多说了,点开响应会看到一些大写英文字母的排列,那是base64编码的结果,可以用
python的base64库中base64.bs64decode将它们解码为字节流再用wb模式写入mp4文件即可。不过有些大的视频可能会传输的很慢一般是很难下载得下来的,因为总会失败,不嫌烦可以分块下载,或者去试试自己写一个多线程的下载器,这玩意儿还挺有趣的。 - 至于怎么拿到请求的URL,我看了一阵子js也没找到相关的脚本,如果想写爬虫的话可能还是比较困难,得彻底搞清楚这个复杂的请求url是怎么来的,不过倒是可以写点浏览器内嵌的js来协助,这应该会相对简单。油猴上面是有用户脚本的,不过也并非万能,毕竟b站数以亿计的视频,不可能用一种方法能全部搞定的,总有很多情况不适用于这种方法,我其实看油猴里有些人做了一些好玩的工作,比如跳过大会员限制看番之类的,确实还挺有趣~
02-03
- 注意到某人换回了捣蛋鹅的头像,还有的同学似乎刚走。
- 前两天每日12km,今天6km,大致如此,感觉左膝伤一直在,不敢路跑长距离,痛苦的休整期。
- 吹爆逆转裁判,名侦探柯南到底还是逊色了一些。
- adb关键事件(一)
电话键
KEYCODE_CALL 拨号键 5
KEYCODE_ENDCALL 挂机键 6
KEYCODE_HOME 按键Home 3
KEYCODE_MENU 菜单键 82
KEYCODE_BACK 返回键 4
KEYCODE_SEARCH 搜索键 84
KEYCODE_CAMERA 拍照键 27
KEYCODE_FOCUS 拍照对焦键 80
KEYCODE_POWER 电源键 26
KEYCODE_NOTIFICATION 通知键 83
KEYCODE_MUTE 话筒静音键 91
KEYCODE_VOLUME_MUTE 扬声器静音键 164
KEYCODE_VOLUME_UP 音量增加键 24
KEYCODE_VOLUME_DOWN 音量减小键 25
02-04
- 最近在做一些收集语料的工作,以备后用。
- 感觉巧舟回归后,逆6没有前三部那个味道了,加了美贯,王泥喜,心音后太乱了,而且逆转前三部差不多是把坑都填了,是一个完整的故事链,后续再强行开篇章没有之前的感觉了。看完逆3最后一章华丽的逆转,除了震惊就是震惊。
dot命令概述及使用方法:
- 命令路径:
E:\Graphviz\bin\dot.exe;- 注意没有添加到系统环境变量中, 只添加在用户
caoyang的环境变量中, 所以调用python的os.system('dot')方法将无效, 可以修改为os.system(r'E:\Graphviz\bin\dot.exe')即可;
- 注意没有添加到系统环境变量中, 只添加在用户
- 调用方法:
- 方法一: 常规shell脚本调用;
- 将下面的代码保存到
test.dot文件中后, 在同级目录下执行指令dot -Tpng -o test.png test.dot即可在同级目录下生成test.png图片;digraph G { # 定义全局属性 fontname = "Courier New" fontsize = 8 # 从下往上 rankdir = BT # 定义节点属性 node [ shape = "record" # 矩形,默认是椭圆 color = "blue" # 边框蓝色 ] # 定义边的属性 edge [ fontsize = 9 ] # 换行符是\l,而要新建一个新的单元格,则需要是用|。{}里面的是内容 Reportable [ label = "{Reportable | + getSummary() : Map\<String, Integer\> | + getDetail() : Map\<String, Integer\> | + isDetailVisible() : boolean}" ] # 特殊字符要转义 LineCounter [ label = "{LineCounter | + count(String line) : boolean | + getType() : String}" ] CharCounter [ label = "{CharCounter | + count(Character c) : boolean | + getType() : String}" ] AbstractCharCounter [ label = "{AbstractCharCounter | characterMap : Map\<Character, Integer\> | + count(Character c) : boolean | + getSummary() : Map\<String, Integer\> | +getDetail() : Map\<String, Integer\> }" ] AbstractLineCounter [ label = "{AbstractLineCounter | + count(String line) : boolean | + getSummary() : Map\<String, Integer\> | +getDetail() : Map\<String, Integer\> }" ] PredicateCharacter[label = "{Predicate\<Character\> | + apply(Character c) : boolean}"] PredicateString[label = "{Predicate\<String\> | + apply(String line) : boolean}"] BlankCharCounter[label = "{BlankCharCounter | + apply(Character c) : boolean | + getType() : String | + isDetailVisible() : boolean }"] ChineseCharCounter[label = "{ChineseCharCounter | - chinesePattern : Pattern | + apply(Character c) : boolean | + getType() : String | + isDetailVisible() : boolean }"] LetterCharCounter[label = "{LetterCharCounter | - chinesePattern : Pattern | + apply(Character c) : boolean | + getType() : String | + isDetailVisible() : boolean }"] NumberCharCounter[label = "{NumberCharCounter | + apply(Character c) : boolean | + getType() : String | + isDetailVisible() : boolean }"] LineNumberCounter[label = "{LineNumberCounter | + apply(Character c) : boolean | + getType() : String | + isDetailVisible() : boolean }"] parentInterface [label = "parent interface" color = "green" style=filled] childInterface [label = "child interface" color = "green" style=filled] abstractClass [ label = "abstract class : implement some methods using the abstract methods" color = "green" style=filled] specificClass [ label = "specific class : implement all unimplemented methods" color = "green" style=filled] LineProcessor [label = "{LineProcessor\<List\<Reportable\>\>}" ] ReportableLineProcessor [ label = "{ReportableLineProcessor | + ReportableLineProcessor() | + processsLine(String line) : boolean | + getResult() : List\<Reportable\>}"] # 定义在同一层 {rank = same; parentInterface; Reportable; LineProcessor} {rank = same; childInterface; LineCounter; CharCounter; PredicateCharacter; PredicateString} {rank = same; abstractClass; AbstractLineCounter; AbstractCharCounter;} {rank = same; specificClass; LineNumberCounter; BlankCharCounter; ChineseCharCounter; LetterCharCounter; NumberCharCounter; ReportableLineProcessor} # 箭头为空心,接口之间的继承 LineCounter -> Reportable[arrowhead="empty"] CharCounter -> Reportable[arrowhead="empty"] AbstractCharCounter -> CharCounter[arrowhead="empty"] AbstractLineCounter -> LineCounter[arrowhead="empty"] AbstractCharCounter -> PredicateCharacter[arrowhead="empty"] AbstractLineCounter -> PredicateString[arrowhead="empty"] # 实现类的UML BlankCharCounter -> AbstractCharCounter[arrowhead="empty", style="dashed"] ChineseCharCounter -> AbstractCharCounter[arrowhead="empty", style="dashed"] LetterCharCounter -> AbstractCharCounter[arrowhead="empty", style="dashed"] NumberCharCounter -> AbstractCharCounter[arrowhead="empty", style="dashed"] LineNumberCounter -> AbstractLineCounter[arrowhead="empty", style="dashed"] ReportableLineProcessor -> LineProcessor[arrowhead="empty", style="dashed"] }
- 将下面的代码保存到
- 方法二:
python脚本中的调用;- 首先使用
os.popen()函数打开一个管道:f = popen(r"E:\Graphviz\bin\dot -Tpng -o %s.png" % file, 'w'); - 将方法一中
test.dot文件中的所有代码以字符串的形式写入管道:f.write(dot_command); - 最后关闭文件:
f.close()
- 首先使用
- 方法一: 常规shell脚本调用;
02-05
- GCX今天早上的飞机去的加拿大,大约gap了半年,最终还是出去了,听到这个消息都无感了。
- 烦躁,腿伤未愈。
- 小脚本
# -*- coding: UTF-8 -*-
# Author: Cao Yang
# 酷我音乐爬虫模块
import os
import sys
import math
import time
import json
import random
import base64
import codecs
sys.path.append("../") # 导入上级目录
from requests import Session
from bs4 import BeautifulSoup
from Crypto.Cipher import AES # 这个库安装的话直接安装pycryptodome, 如果安装Crypto会有些不友好的问题
from selenium import webdriver
from selenium.webdriver.common.keys import Keys
from selenium.webdriver.support.ui import WebDriverWait
from selenium.webdriver.common.action_chains import ActionChains
from FC_crawl import Crawl
from FC_utils import *
class KuWo(Crawl): # 酷我音乐爬虫
def __init__(self):
Crawl.__init__(self) # 父类继承
# 类常用参数
self.url_main = "http://www.kuwo.cn/" # 网易云音乐首页
self.headers = {"User-Agent": self.user_agent} # 请求头伪装信息
self.url_api = self.url_main + "url" # 请求歌曲链接的接口
self.api_params = { # 接口调用参数
"format": "mp3", # 返回格式
"rid": None, # 歌曲编号
"response": "url", # 返回变量
"type": "convert_url3", # 返回类型
"br": "128kmp3", # 返回歌曲质量
"from": "web", # 请求来源
"t": None, # 时间戳
"reqId": "", # 关于这个字段的生成我目前细究, 因为目前不带这个字段也是可行的
}
self.url_song = "http://www.kuwo.cn/play_detail/{}" # 歌曲页面链接
# 类初始化操作
self.renew_session() # 生成新的session对象
def renew_session(self): # 重构
self.session = Session() # 创建新的Session对象
self.session.headers = self.headers.copy() # 伪装头部信息
self.session.get(self.url_main) # 访问主页
def search_for_song_id(self,song_name,driver,
n_result=1, # 返回多少个查询结果
):
pass
def download_by_song_id(self,song_id, # 给定歌曲编号
save_path=None, # 歌曲下载保存路径
driver=None,
): # 通过歌曲编号下载歌曲
song_url = self.request_for_song_url(song_id,driver=driver) # 获取歌曲链接
r = self.session.get(song_url) # 访问歌曲链接
if save_path is None: save_path = "kuwo_{}".format(song_id) # 默认的保存路径
with open(save_path,"wb") as f: f.write(r.content) # 写入音乐文件
def request_for_song_url(self,song_id,
driver=None,
): # 请求歌曲链接
params = self.api_params.copy() # 获取请求字符串
params["rid"] = song_id # 设置歌曲编号
params["t"] = int(time.time()*1000) # 设置时间戳
r = self.session.get(self.url_api,params=params) # 发出播放请求
print(r.text)
song_url = json.loads(r.text)["url"] # 这里用eval不好使, 因为有python无法识别为缺失值的null
return song_url
def test(self):
song_id = "90785562"
r = self.download_by_song_id(
song_id,
save_path="kuwo_{}.mp3".format(song_id),
driver=None,
)
if __name__ == "__main__":
kw = KuWo()
kw.test()
02-06
- 周跑54km,明天还有一天,目测回家一个月的月跑量能上到230km左右。
- CSDN又犯病了。
- functools杂记
functools.reduce: 将列表中所有元素连乘- 代码示例:
from functools import reduce lt = [1, 2, 3, 4, 5] ln = reduce(lambda x, y: x * y, lt) print(ln)- 输出结果:
120;
- 输出结果:
- 代码示例:
02-07
- 挣扎了很多天终于回归了正轨。
- 今天又有人跟我提GCX去加拿大的事情,可能是我墨守成规,我总是觉得女生没有必要在这种局势下去那么远的地方留学,别人不知道,我怎么会不清楚,gcx本科四年显然也没有尽全力,会院去加拿大的都是较次的一批学生了。本科四年,改变我们太多太多,有些从前再也回不去了。
- 昨日10km后腿伤加剧,右膝有刺痛感,还想着年前能跑一次20km,还是太年轻了。
- 百度翻译2021最新的解密方法已经找到,近期更新思路,先给出核心脚本:
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
import json
import execjs
import requests
from bs4 import BeautifulSoup
from urllib.parse import urlencode
class BaiduFanyi(object):
""""""
def __init__(self) -> None:
javascript_code = '''function n(r,o){for(var t=0;t<o.length-2;t+=3){var a=o.charAt(t+2);a=a>="a"?a.charCodeAt(0)-87:Number(a),a="+"===o.charAt(t+1)?r>>>a:r<<a,r="+"===o.charAt(t)?r+a&4294967295:r^a}return r}var i=null;function e(r,gtk){var o=r.match(/[\uD800-\uDBFF][\uDC00-\uDFFF]/g);if(null===o){var t=r.length;t>30&&(r=""+r.substr(0,10)+r.substr(Math.floor(t/2)-5,10)+r.substr(-10,10))}else{for(var e=r.split(/[\uD800-\uDBFF][\uDC00-\uDFFF]/),C=0,h=e.length,f=[];h>C;C++)""!==e[C]&&f.push.apply(f,a(e[C].split(""))),C!==h-1&&f.push(o[C]);var g=f.length;g>30&&(r=f.slice(0,10).join("")+f.slice(Math.floor(g/2)-5,Math.floor(g/2)+5).join("")+f.slice(-10).join(""))}var u=void 0,l=""+String.fromCharCode(103)+String.fromCharCode(116)+String.fromCharCode(107);u=null!==i?i:(i=gtk||"")||"";for(var d=u.split("."),m=Number(d[0])||0,s=Number(d[1])||0,S=[],c=0,v=0;v<r.length;v++){var A=r.charCodeAt(v);128>A?S[c++]=A:(2048>A?S[c++]=A>>6|192:(55296===(64512&A)&&v+1<r.length&&56320===(64512&r.charCodeAt(v+1))?(A=65536+((1023&A)<<10)+(1023&r.charCodeAt(++v)),S[c++]=A>>18|240,S[c++]=A>>12&63|128):S[c++]=A>>12|224,S[c++]=A>>6&63|128),S[c++]=63&A|128)}for(var p=m,F=""+String.fromCharCode(43)+String.fromCharCode(45)+String.fromCharCode(97)+(""+String.fromCharCode(94)+String.fromCharCode(43)+String.fromCharCode(54)),D=""+String.fromCharCode(43)+String.fromCharCode(45)+String.fromCharCode(51)+(""+String.fromCharCode(94)+String.fromCharCode(43)+String.fromCharCode(98))+(""+String.fromCharCode(43)+String.fromCharCode(45)+String.fromCharCode(102)),b=0;b<S.length;b++)p+=S[b],p=n(p,F);return p=n(p,D),p^=s,0>p&&(p=(2147483647&p)+2147483648),p%=1e6,p.toString()+"."+(p^m)}'''
self.javascript_lambda = execjs.compile(javascript_code)
self.headers = {
'Host' : 'fanyi.baidu.com',
'User-Agent' : 'Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:82.0) Gecko/20100101 Firefox/82.0',
'Accept' : 'text/html,application/xhtml+xml,application/xml;q=0.9,image/webp,*/*;q=0.8',
'Accept-Language' : 'zh-CN,zh;q=0.8,zh-TW;q=0.7,zh-HK;q=0.5,en-US;q=0.3,en;q=0.2',
'Accept-Encoding' : 'gzip, deflate, br',
'Connection' : 'keep-alive',
'Cookie' : 'BAIDUID=57D8DECD1001EDF4A260905A983072A9:FG=1; BIDUPSID=57D8DECD1001EDF4A260905A983072A9; PSTM=1612680499; BDRCVFR[gltLrB7qNCt]=mk3SLVN4HKm; delPer=0; PSINO=5; H_PS_PSSID=33425_33355_33273_33585; BA_HECTOR=2g8g240g0h00ak24451g1v39k0r; BDORZ=FFFB88E999055A3F8A630C64834BD6D0; Hm_lvt_64ecd82404c51e03dc91cb9e8c025574=1612680504,1612680509; Hm_lpvt_64ecd82404c51e03dc91cb9e8c025574=1612680509; __yjs_duid=1_57795229af6fbff1bde0f88f5beda8381612680504436; ab_sr=1.0.0_ZGQxNTEyYzNmYmM3YzA3ODgxMTIzNzhkNTQ2MDg4ODU2ZDAxODNlODQxZjJlYzdkNDNhNjhlYjIyNWNlZjIxNmIzOTE2YzgxNjJjMTExMzlkMWY5NWQzOTUxMTkzYWZi; __yjsv5_shitong=1.0_7_f89862c9f80b86296408413c2a5c443713a1_300_1612680509895_49.95.205.54_60776bff; REALTIME_TRANS_SWITCH=1; FANYI_WORD_SWITCH=1; HISTORY_SWITCH=1; SOUND_SPD_SWITCH=1; SOUND_PREFER_SWITCH=1',
'Upgrade-Insecure-Requests' : '1',
}
self.mainpage_url = 'https://fanyi.baidu.com/'
self.transapi_url = 'https://fanyi.baidu.com/v2transapi'
self.result = None
def v2transapi(self, keyword: str, source: str='en', target: str='zh') -> dict:
session = requests.Session()
session.headers = self.headers.copy()
'''
response = session.get(self.mainpage_url, headers=self.headers)
html = response.text
with open('baidufanyi.html', 'w', encoding='utf8') as f:
f.write(html)
'''
with open('baidufanyi.html', 'r', encoding='utf8') as f:
html = f.read()
def _find_token_and_gtk(html: str) -> (str, str):
soup = BeautifulSoup(html, 'lxml')
scripts = soup.find_all('script')
script_code = '''var window={};try{'''
for script in scripts:
_script_code = str(script.string).strip('\n')
if _script_code.startswith('window'):
script_code += _script_code + ''';'''
script_code += '''}catch(e){}'''
window = execjs.compile(script_code).eval('window')
token = window['common']['token']
gtk = window['gtk']
return token, gtk
token, gtk = _find_token_and_gtk(html)
formdata = {
'from' : source,
'to' : target,
'query' : keyword,
'simple_means_flag' : '3',
'sign' : self.javascript_lambda.call('e', keyword, gtk),
'token' : token,
'domain' : 'common',
}
# print(urlencode(formdata))
response = session.post(self.transapi_url, data=formdata)
result = response.json()
with open('transapi_{}.json'.format(keyword), 'w', encoding='utf8') as f:
json.dump(result, f)
return result
02-08
- 发现某人很有趣,礼尚往来。
- 精心写了一篇博客作为年关收尾,不过确实是一个挺不错的爬虫训练。
- 20km跑,终会达成。
- Linux的一些杂记:
ssh root@101.132.103.34 连接远程服务器
ls -a 查看当前目录下的文件与文件夹
cd <文件夹> 进入文件夹
cd .. 返回上级目录
rm <文件名> 删除文件
rm -f <文件名> 强制删除文件
rm -r <文件夹名> 删除文件夹
mkdir 目录名 (新建一个文件夹,文件夹在Linux系统中叫做“目录”)
touch 文件名 (新建一个空文件)
rmdir 目录名 (删除一个空文件夹,文件夹里有内容则不可用)
rm -rf 非空目录名 (删除一个包含文件的文件夹)
rm 文件名 文件名 (删除多个文件)
cp 文件名 目标路径(拷贝一个文件到目标路径,如cp hserver /opt/hqueue)
cp -i (拷贝,同名文件存在时,输出 [yes/no] 询问是否执行)
cp -f (强制复制文件,如有同名不询问)
dpkg -S 软件名 (用apt安装的软件目录)
ps aux 查看所有进程
crontab:
SHELL=/bin/bash
PATH=/sbin:/bin:/usr/sbin:/usr/bin
MAILTO=root
HOMR=/
0 18 * * 1-5 root /root/智能投顾小信/Update/Beginner.py
nohup python -u nndial_interact.py >nndial.log 2>&1 &tail -f nndial.log
nohup python -u Beginner.py >Beginner.log 2>&1 &tail -f Beginner.log
nohup python -u manage.py runserver 0.0.0.0:8000 >manage.log 2>&1 &tail -f manage.log
nohup python -u CSDN.py >CSDN.log 2>&1 &tail -f CSDN.log
nohup python3.6 CSDN.py >CSDN.log 2>&1 &
查看磁盘占用
du -sh
du -h
du -h <文件夹名>
查看内存占用
free -h
任务管理器
top
绝对路径
/root/.. 在前面添加一个斜杠则默认为绝对路径
查看系统位数
sudo uname --m
anaconda 创建 环境:conda create -n py2 python=2.7
无法使用conda命令怎么办:输入上面两句即可
export PATH="/root/anaconda3/bin:PATH" >> ~/.bashrc
source ~/.bashrc
conda --version
改变python版本
alias python="/root/anaconda3/bin/python3.6"
查看文件管理系统: df
02-09
- 王英林给发了PIC的会务费,出手还挺豪爽的,没想到会给这么多… 先礼后兵,然后就让我考虑一下IUI的研究,就很让人绝望,我怎么知道这玩意儿怎么搞,大过年的,不会是这时候要动工吧。
- 现在有时候感觉膝盖头是肿的,有时候又什么感觉都没有,挤按左膝头还是会疼,真的是恢复不了了吗,天天跑步机实在是没有长进。
- ADB关键事件(二)
控制键
KEYCODE_ENTER 回车键 66
KEYCODE_ESCAPE ESC键 111
KEYCODE_DPAD_CENTER 导航键 确定键 23
KEYCODE_DPAD_UP 导航键 向上 19
KEYCODE_DPAD_DOWN 导航键 向下 20
KEYCODE_DPAD_LEFT 导航键 向左 21
KEYCODE_DPAD_RIGHT 导航键 向右 22
KEYCODE_MOVE_HOME 光标移动到开始键 122
KEYCODE_MOVE_END 光标移动到末尾键 123
KEYCODE_PAGE_UP 向上翻页键 92
KEYCODE_PAGE_DOWN 向下翻页键 93
KEYCODE_DEL 退格键 67
KEYCODE_FORWARD_DEL 删除键 112
KEYCODE_INSERT 插入键 124
KEYCODE_TAB Tab键 61
KEYCODE_NUM_LOCK 小键盘锁 143
KEYCODE_CAPS_LOCK 大写锁定键 115
KEYCODE_BREAK Break/Pause键 121
KEYCODE_SCROLL_LOCK 滚动锁定键 116
KEYCODE_ZOOM_IN 放大键 168
KEYCODE_ZOOM_OUT 缩小键 169
02-10
- 电灯泡逛了一天街,晚上回来以为酒饱饭足可以大跑一通,结果8km就跪了,可能还是白天逛街脚走得酸了,年前破20km的梦想就此幻灭,遗憾透顶。
- 金钱会使人膨胀,金钱也会使人毁灭。
- 老妈偷看了我的日记,知道我的左右膝盖都在痛,之前一直瞒着她,但是今晚她还是陪我一起出门跑,老妈问我为什么执着于要跑半马,也许没什么原因,就是想去跑,很朴素的愿望。
- java.lang.Thread类
- 构造函数:
- Thread(Runnable target)
- Thread(String string)
- 方法:
- .sleep()——停止
- .yield()——同级别线程上位
- .join()——等待直到当前线程结束
- .interrupt()
- .currentThread()——返回当前线程的引用
- .isAlive()——是否运行
- 线程交互wait()与notify()、notifuAll()
- .stop():强制结束
- .suspend()与.resume()——暂停执行再次运行
02-11
- 大年三十,一天奔波,疲累不堪。
- 不久就快开学了,假期余额又不足了,唉。
- R语言中字符串处理小结
如果是连接字符串最快的方法用library(stringr)->str_c("A","B")->"AB"
x <- c("Hellow", "World", "!")
nchar(x)
[1] 6 5 1
length("")
[1] 1
nchar("")
[1] 0
DNA <- "AtGCtttACC"
tolower(DNA)
## [1] "atgctttacc"
toupper(DNA)
## [1] "ATGCTTTACC"
chartr("Tt", "Uu", DNA)
## [1] "AuGCuuuACC"
chartr("Tt", "UU", DNA)
## [1] "AUGCUUUACC"
paste("CK", 1:6, sep = "")
## [1] "CK1" "CK2" "CK3" "CK4" "CK5" "CK6"
x <- list(a = "aaa", b = "bbb", c = "ccc")
y <- list(d = 1, e = 2)
paste(x, y, sep = "-") #较短的向量被循环使用
## [1] "aaa-1" "bbb-2" "ccc-1"
z <- list(x, y)
paste("T", z, sep = ":")
## [1] "T:list(a = \"aaa\", b = \"bbb\", c = \"ccc\")"
## [2] "T:list(d = 1, e = 2)"
as.character(x)
## [1] "aaa" "bbb" "ccc"
as.character(z)
## [1] "list(a = \"aaa\", b = \"bbb\", c = \"ccc\")"
## [2] "list(d = 1, e = 2)"
paste函数还有一个用法,设置collapse参数,连成一个字符串:
paste(x, y, sep = "-", collapse = "; ")
## [1] "aaa-1; bbb-2; ccc-1"
paste(x, collapse = "; ")
## [1] "aaa; bbb; ccc"
text <- "Hello Adam!\nHello Ava!"
strsplit(text, " ")
## [[1]]
## [1] "Hello" "Adam!\nHello" "Ava!"
R语言的字符串事实上也是正则表达式,上面文本中的\n在图形输出中是被解释为换行符的。
strsplit(text, "\\s")
## [[1]]
## [1] "Hello" "Adam!" "Hello" "Ava!"
strsplit得到的结果是列表,后面要怎么处理就得看情况而定了:
class(strsplit(text, "\\s"))
## [1] "list"
有一种情况很特殊:如果split参数的字符长度为0,得到的结果就是一个个的字符:
strsplit(text, "")
## [[1]]
## [1] "H" "e" "l" "l" "o" " " "A" "d" "a" "m" "!" "\n" "H" "e"
## [15] "l" "l" "o" " " "A" "v" "a" "!"
02-12
- 大年初一,与服役的表哥长聊了一次,有所感。
- 使用EXCEL的小TIP
(一)交叉合并两列数据
把需要交叉合并的数据分别放在A列和B列
在任意非A, B列中的单元格写入公式:
=OFFSET(A$1,INT((ROW(A1)-1)/2),MOD(ROW(A1)-1,2))
再一路拉下去即可
02-13
- 大年初二,迎财神。
- wordnet用了一下,这玩意儿居然还有个exe的版本,还挺不错的,有空研究一下。
- matlab绘图:
例 用不同的线型和颜色在同一坐标内绘制曲线 及其包络线。
>> x=(0:pi/100:2*pi)';
>> y1=2*exp(-0.5*x)*[1,-1];
>> y2=2*exp(-0.5*x).*sin(2*pi*x);
>> x1=(0:12)/2;
>> y3=2*exp(-0.5*x1).*sin(2*pi*x1);
>> plot(x,y1,'k:',x,y2,'b--',x1,y3,'rp');
02-14
- 回家后的第一天不跑步,腿伤的太重了,不敢再强行起跑了,连跑步机都不敢上,这样一来回家4个整周,跑量分别为52km,56km,62km,26km,累积勉强接近200km的目标。
- 下午一家去凤凰岛玩了半天,好久没一家三口出来玩了,人很多,才发现是情人节。
- pywin32库一些测试:
import win32gui,win32ui,win32con
'''
def get_windows(windowsname,filename):
# 获取窗口句柄
handle = win32gui.FindWindow(None,windowsname)
# 将窗口放在前台,并激活该窗口(窗口不能最小化)
win32gui.SetForegroundWindow(handle)
# 获取窗口DC
hdDC = win32gui.GetWindowDC(handle)
# 根据句柄创建一个DC
newhdDC = win32ui.CreateDCFromHandle(hdDC)
# 创建一个兼容设备内存的DC
saveDC = newhdDC.CreateCompatibleDC()
# 创建bitmap保存图片
saveBitmap = win32ui.CreateBitmap()
# 获取窗口的位置信息
left, top, right, bottom = win32gui.GetWindowRect(handle)
# 窗口长宽
width = right - left
height = bottom - top
# bitmap初始化
saveBitmap.CreateCompatibleBitmap(newhdDC, width, height)
saveDC.SelectObject(saveBitmap)
saveDC.BitBlt((0, 0), (width, height), newhdDC, (0, 0), win32con.SRCCOPY)
saveBitmap.SaveBitmapFile(saveDC, filename)
get_windows("PyWin32","截图.png")
'''
'''
import time
import win32gui,win32con
import keyboardEmulation as ke
def get_windows(windowsname,filename):
# 获取窗口句柄
hwnd = win32gui.FindWindow(None,windowsname)
# 将窗口放在前台,并激活该窗口
win32gui.SetForegroundWindow(hwnd)
# 输入helloworld
scancodes = [0x23, 0x12, 0x26, 0x26, 0x18, 0x11, 0x18, 0x13, 0x26, 0x20, 0x2a]
for code in scancodes:
ke.key_press(code)
# 保存
ke.key_down(0x1d)
ke.key_down(0x1f)
ke.key_up(0x1d)
ke.key_up(0x1f)
# 关闭窗口
time.sleep(1);
win32gui.PostMessage(hwnd, win32con.WM_CLOSE, 0, 0)
get_windows("新建文本文档 (2).txt - 记事本","截图.png")
'''
import win32gui
import win32process
import win32con
import win32api
import ctypes
PROCESS_ALL_ACCESS = ( 0x000F0000 | 0x00100000 | 0xFFF )
hwnd = win32gui.FindWindow(0, "Form1")
hid,pid = win32process.GetWindowThreadProcessId(hwnd)
phand = win32api.OpenProcess(PROCESS_ALL_ACCESS, False, pid)
date = ctypes.c_long()
mydll = ctypes.windll.LoadLibrary("C:\Windows\System32\kernel32.dll")
mydll.ReadProcessMemory(int(phand) ,0x0039A778,ctypes.byref(date),4,None)
print (date.value)
02-15
- MBAlib
#-*- coding:UTF-8 -*-
import os
import re
import sys
import time
import numpy
import random
import pandas
import requests
from bs4 import BeautifulSoup,element
from selenium import webdriver
from multiprocessing import Process
class MBAlib():
def __init__(self,
userAgent="Mozilla/5.0 (Windows NT 10.0; WOW64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/71.0.3578.98 Safari/537.36",
phantomPath="E:/Python/phantomjs-2.1.1-windows/bin/phantomjs.exe",
driver=True, ):
""" 设置类构造参数 """
self.userAgent = userAgent # 设置浏览器用户代理
self.phantomPath = phantomPath
""" 设置类常用参数 """
self.workspace = os.getcwd() # 获取当前工作目录
self.date = time.strftime("%Y%m%d") # 获取类初始化的时间
self.labelCompiler = re.compile(r"<[^>]+>",re.S) # 标签正则编译
self.entryCount = 0 # 记录已经爬取的条目数量
self.mainURL = "https://www.mbalib.com/" # MBA首页URL
self.wikiURL = "https://wiki.mbalib.com/" # MBA百科URL
self.searchURL = self.mainURL + "s?q={}" # MBA搜索URL
self.wikisearchURL = self.wikiURL + "wiki/Special:Search?search={}&fulltext=搜索"
self.entryURL = self.wikiURL + "wiki/{}" # MBA条目URL
self.indexURL = self.wikiURL + "wiki/MBA智库百科:分类索引" # MBA词条分类索引页面URL
self.categoryURL = self.wikiURL + "wiki/Category:{}" # MBA词条类别页面URL
self.session = requests.Session() # 类专用session
self.myHeaders = {"User-Agent":self.userAgent} # 爬虫头信息
self.imageFolder = "image" # 存放图片词条的子文件夹
self.entryFolder = "entry" # 存放词条文本的子文件夹
self.logFolder = "log" # 存放程序运行的子文件夹
self.log = "{}/log.txt".format(self.logFolder) # 记录文件
self.categoryWait = "{}/categoriyWait.txt".format(self.logFolder)# 记录队列中所有的类别文件
self.categoryDone = "{}/categoriyDone.txt".format(self.logFolder)# 记录已经获取完毕的类别文件
if driver: self.webdriver = webdriver.Firefox() # 初始化火狐浏览器
""" 初始化操作 """
self.session.headers = self.myHeaders # 设置session
self.session.get(self.mainURL) # 定位主页
if not os.path.exists("{}\\{}".format(self.workspace,self.date)):# 每个交易日使用一个单独的文件夹(用日期命名)存储金融数据
print("正在新建文件夹以存储{}MBA智库的数据...".format(self.date))
os.mkdir("{}\\{}".format(self.workspace,self.date))
os.mkdir("{}\\{}\\{}".format(self.workspace,self.date,self.imageFolder))
os.mkdir("{}\\{}\\{}".format(self.workspace,self.date,self.entryFolder))
os.mkdir("{}\\{}\\{}".format(self.workspace,self.date,self.logFolder))
def parse_entries(self,entries,
driver=False,
cycle=100,
minInterval=60,
maxInterval=90,
): # 给定词条列表获取它们所有的信息
for entry in entries:
if driver:
self.webdriver.get(self.entryURL.format(entry))
html = self.webdriver.page_source
else:
html = self.session.get(self.entryURL.format(entry)).text
self.entryCount += 1
if self.entryCount%cycle==0:
interval = random.uniform(minInterval,maxInterval)
time.sleep(interval)
print("获取到第{}个条目 - 暂停{}秒...".format(self.entryCount,interval))
string = "正在获取条目{}...".format(entry)
print(string)
with open("{}/{}".format(self.date,self.log),"a") as f:
f.write("{}\t{}\n".format(string,time.strftime("%Y-%m-%d %H:%M:%S")))
soup = BeautifulSoup(html,"lxml")
if entry[:6]=="Image:": # 图片词条保存为图片
img = soup.find("img")
imageURL = self.wikiURL + img.attrs["src"][1:]
byte = self.session.get(imageURL).text
with open("{}/{}/{}".format(self.date,self.imageFolder,entry[6:]),"wb") as f: f.write(byte)
else: # 非图片词条处理相对麻烦
for script in soup.find_all("script"): script.extract() # 删除脚本
p = soup.find("p") # 从第一个<p>标签的前一个标签开始搞
label = p if isinstance(p.previous_sibling,element.NavigableString) else p.previous_sibling
text = str() # 最终text被写入文本
while True:
if isinstance(label,element.NavigableString): # 下一个平行节点有可能是字符串, 那就扔了
label = label.next_sibling
continue
if not label: break # 没有下一个平行节点, 那就再见
if "class" in label.attrs.keys() and \
label.attrs["class"][0]=="printfooter": break # 页脚处与空标签处暂停
string = self.labelCompiler.sub("",str(label))
text += "{}\n".format(string.strip())
label = label.next_sibling
_nCompiler = re.compile(r"\n+",re.S)
text = _nCompiler.sub("\n",text)
with open("{}/{}/{}.txt".format(self.date,self.entryFolder,entry),"a",encoding="UTF-8") as f:
f.write(text)
def parse_categories(self,categories): # 以参数列表中的条目为根目录, 穿透根目录就完事了
with open("{}/{}".format(self.date,self.categoryWait),"a") as f: # 将传入的所有类别记录到categoryWait.txt中
for category in categories: f.write("{}\n".format(category))
for category in categories:
with open("{}/{}".format(self.date,self.categoryDone),"a") as f: f.write("{}\n".format(category))
subCategories = list() # 存储该category下的所有亚类
entries = list() # 存储该category下的所有条目
html = self.session.get(self.categoryURL.format(category)).text
count = 0
while True:
flag = True # flag用于判断是否还存在下一页
count += 1
soup = BeautifulSoup(html,"lxml")
divs1 = soup.find_all("div",class_="CategoryTreeSection")# 子类超链接
divs2 = soup.find_all("div",class_="page_ul") # 条目超链接
if divs1:
for div in divs1:
aLabel = div.find_all("a")
for a in aLabel:
if str(a.string)=="+": continue # "+"号是一个特殊的书签超链接
subCategories.append(str(a.string))
if divs2:
for div in divs2:
aLabel = div.find_all("a")
for a in aLabel:
if a.attrs["title"][:6]=="Image:": entries.append("Image:{}".format(a.string))
else: entries.append(str(a.string))
string = "正在处理{}类别第{}页的信息 - 共{}个子类{}个条目...".format(category,count,len(subCategories),len(entries))
print(string)
with open("{}/{}".format(self.date,self.log),"a") as f:
f.write("{}\t{}\n".format(string,time.strftime("%Y-%m-%d %H:%M:%S")))
buttons = soup.find_all("a",title="Category:{}".format(category))
if buttons: # 可能并没有这个按钮
for button in buttons:
if str(button.string)[0]=="后":
nextURL = self.wikiURL + button.attrs["href"][1:]
html = self.session.get(nextURL).text # 进入下一页
flag = False # flag高高挂起
break # 退出循环
if flag: break # flag为True无非两种情况: 没有button, 或者只要前200页的button
string = "开始获取{}类别下所有条目信息...".format(category)
print(string)
with open("{}/{}".format(self.date,self.log),"a") as f:
f.write("{}\t{}\n".format(string,time.strftime("%Y-%m-%d %H:%M:%S")))
self.parse_entries(entries,False) # 爬取当前类别的条目
string = "开始获取{}类别下所有亚类信息...".format(category)
print(string)
with open("{}/{}".format(self.date,self.log),"a") as f:
f.write("{}\t{}\n".format(string,time.strftime("%Y-%m-%d %H:%M:%S")))
self.parse_categories(subCategories) # 爬取当前类别的亚类
def parse_index_page(self,): # 爬取MBA词条分类索引页面
print("正在获取MBA索引页面信息...")
html = self.session.get(self.indexURL).text
soup = BeautifulSoup(html,"lxml")
h2s = soup.find_all("h2") # 由于<div>标签过于混乱, 采用<h2>标签来定位不同分类
categories = dict()
for h2 in h2s:
tempList = list()
div = h2.find_parent().next_sibling.next_sibling # 经验之谈, 没有为什么
ps = div.find_all("p") # <p>标签索引每行第一个类别
for p in ps:
a = p.find("a") # 只要第一个<a>标签即可因为后面的都可以在第一个类别的亚类或者次亚类中寻找到
if a: tempList.append(str(a.string)) # 存在<a>标签则取第一个
else: # 不存在<a>标签的情况比较复杂, 总的来说是MBAlib网页设计者实在是太垃圾了
label = p.find_next_sibling("p") # 后续平行结点还有<p>标签定位
label = label if label else p.find_next_sibling("dl")# 否则定位<dl>标签
aLabel = label.find_all("a") # "其他/它"类别下的所有类别, 互相平行所以全都要
for a in aLabel: tempList.append(str(a.string))
break
categories[str(h2.string)] = tempList # 考虑到未必需要全部词条,因此这里把根条目按照六类分别存入字典
print("索引页面信息获取完毕!\n共有{}个大类,{}个根条目".format(len(categories.keys()),sum(len(value) for value in categories.values())))
return categories
def search(self,keyword): # 使用MBA智库搜索引擎, 返回搜索到的"百科"条目
html = self.session.get(self.searchURL.format(keyword)).text
soup = BeautifulSoup(html,"lxml")
h3s = soup.find_all("h3")
results = [] # 获取搜索到的"百科"条目
for h3 in h3s:
s = h3.find("span",class_="pd-top")
if str(s.string)=="百科":
s.extract()
string = self.labelCompiler.sub("",str(h3))
results.append(string)
for result in results:
print(result)
return results
def search_wiki(self,keyword): # 搜索MBA智库百科词条, 返回至多前十个搜索词条
html = self.session.get(self.wikisearchURL.format(keyword)).text
soup = BeautifulSoup(html,"lxml")
aLabel = soup.find_all("a")
results = []
for a in aLabel:
try:
span = a.find("span")
if "searchmatch" in span.attrs["class"]:
string = self.labelCompiler.sub("",str(a))
results.append(string.strip())
except:
try: # 这个except里面的内容后来写的,当我搜索"大大大"的时候, 虽然没有<span>匹配项, 但是仍有返回结果因此我又硬代码了一回
if a.attrs["href"][:5]=="/wiki" and len(a.find_parents("b")):
string = self.labelCompiler.sub("",str(a))
results.append(string.strip())
else: continue
except: continue
return results[:10] if len(results)>10 else results
def entry(self,entry,
driver = False
): # 给定词条列表获取它们所有的信息(我打算涉及一下关键词提取的功能)
nonsense = [
"想问一下","想问","想了解一下","想了解","想知道一下","想知道",
"想搞清楚","什么是","是什么意思","是什么","什么意思","何为",
"的定义内容","的定义","我"
]
entry = entry.strip()
for word in nonsense:
entry = entry.replace(word,"")
if driver:
b = webdriver.Firefox()
b.get(self.entryURL.format(entry))
html = b.page_source
b.quit()
else: html = self.session.get(self.entryURL.format(entry)).text
soup = BeautifulSoup(html,"lxml")
title = soup.find("title")
if entry not in str(title.string): return "你要访问的词条不存在",False
for script in soup.find_all("script"): script.extract() # 删除脚本
p = soup.find("p") # 从第一个<p>标签的前一个标签开始搞
label = p if isinstance(p.previous_sibling,element.NavigableString) else p.previous_sibling
text = str() # 最终text被写入文本
while True:
if isinstance(label,element.NavigableString): # 下一个平行节点有可能是字符串, 那就扔了
label = label.next_sibling
continue
if not label: break # 没有下一个平行节点,那就再见
if "class" in label.attrs.keys() and \
label.attrs["class"][0]=="printfooter": break # 页脚处与空标签处暂停
string = self.labelCompiler.sub("",str(label))
text += "{}\n".format(string.strip())
label = label.next_sibling
_nCompiler = re.compile(r"\n+",re.S)
text = _nCompiler.sub("\n",text)
index1 = text.find("[编辑]")
index2 = text.find("[编辑]",index1+1)
return text[index1+4:index2],True
if __name__ == "__main__":
print("开始测试...")
mbalib = MBAlib(driver=False)
#mbalib = MBAlib(driver=False)
#categories = mbalib.parse_index_page()
#mbalib.parse_categories(categories["金融百科"])
#mbalib.parse_entries(["银行资产证券化"])
#mbalib.search("资产证券")
02-16
- 两腿的膝盖都有撕裂感,绑着护膝休息了一天,之后只能轻松跑了,唉,可能要到下半年再加量备战半马了。好好研究研究怎么才能安全地跑步了,没想到竟然会这么伤。
- nltk的corpus可以到网盘里下好用,现在nltk.download()已经不太行了。
'''
import nltk
from pattern.en import lemma
print(nltk.__version__)
from nltk.corpus import wordnet as wn
# 词集
synsets = wn.synsets('dog')
print(synsets)
'''
from transformers import BertTokenizer, BertModel, BertForMaskedLM
'''
bert_tokenizer = BertTokenizer.from_pretrained('bert-base-chinese')
words = bert_tokenizer.tokenize('I love you.')
words = bert_tokenizer.tokenize('我爱你。')
print(words)
bert_tokenizer.add_tokens([chr(i) for i in range(ord("A"), ord("Z") + 1)])
'''
help()
bert_model = BertModel.from_pretrained('bert-base-chinese')
02-17
- 终于是逃得过初一,逃不过十五,被导师给抓回来了。
- 发现一个非常厉害的开源项目:https://github.com/huggingface/transformers,csdn有加速。transformers库里面有很多预训练好的模型,跟tensorflow那些都挂在google上的不同,这里的都可以比较快的下载好,无需翻墙。
- 被迫搞IUI,我连自己到底在做什么都不知道,不知道为什么wyl一定要搞这个烂活。
02-18
- 腿恢复了一些,这几天4~6km在跑步机上做康复性的练习。总之长跑确实对腿脚损伤太大了,只有经历过的才能有感同身受,很羡慕那些跑半马全马如喝水的大神。
- 或许离家前会再跑一次长距离,但是一定会注意防护的了,能跑完半马且不受伤才是终极目标。
- 关于transformers库下载预处理模型的路径,可以去考察transformers源码下的file_utils.py中的几个环境变量,自己设置一下环境变量就不会存储到C盘里的.cache/…/transformers目录下了,目前好像网络上没有相关的回答。
- transformers库值得一看,从其支持的模型与框架来看,pytorch远远优于tensorflow,说起来最近试了一下tf2调用BERT,发现之前的代码改了半天也跑不通,tf2已经完全脱离tf1了,我已经决定不搞tensorflow了,以后能用pytorch就用pytorch,tensorflow真是越搞事越多,还难办。
02-19
- 过几天回去了
- transformers小实例
import transformers
print(transformers.__version__)
from transformers import pipeline
classifier = pipeline('sentiment-analysis')
print(classifier('You are a son of bitch'))
02-20
- 复制一段API文档的内容也算违规了?现在抓的这么紧
- transformers 4.3.x版本收录的模型列表:见https://huggingface.co/transformers/
- 注意看这个链接里的平台列表,pytorch是全部模型都支持,但tensorflow则并不支持全部的模型。
02-21
- 接下来会跟一个基金项目,首先得把30页的科研基金申请书给写完。总算是把自己拉回了现实。
DGL摘录(一)
- DGL定义图的方法并非常见的邻接矩阵或出入度链表形式, 而是直接将所有边的出节点和入节点用两个
list存储, 这样的好处是对于稀疏图(即邻接矩阵系数)可以大大减少存储成本, 且无需额外记录图的节点, 直接将两个list拼接后去重就可以得到所有节点, 不过离群点(出度与入度都为零的节点)是不会被考虑进来的;
- 建图代码如下所示:
import dgl import numpy as np def build_karate_club_graph(): # All 78 edges are stored in two numpy arrays. One for source endpoints # while the other for destination endpoints. src = np.array([1, 2, 2, 3, 3, 3, 4, 5, 6, 6, 6, 7, 7, 7, 7, 8, 8, 9, 10, 10, 10, 11, 12, 12, 13, 13, 13, 13, 16, 16, 17, 17, 19, 19, 21, 21, 25, 25, 27, 27, 27, 28, 29, 29, 30, 30, 31, 31, 31, 31, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33]) dst = np.array([0, 0, 1, 0, 1, 2, 0, 0, 0, 4, 5, 0, 1, 2, 3, 0, 2, 2, 0, 4, 5, 0, 0, 3, 0, 1, 2, 3, 5, 6, 0, 1, 0, 1, 0, 1, 23, 24, 2, 23, 24, 2, 23, 26, 1, 8, 0, 24, 25, 28, 2, 8, 14, 15, 18, 20, 22, 23, 29, 30, 31, 8, 9, 13, 14, 15, 18, 19, 20, 22, 23, 26, 27, 28, 29, 30, 31, 32]) # Edges are directional in DGL; Make them bi-directional. u = np.concatenate([src, dst]) v = np.concatenate([dst, src]) # Construct a DGLGraph return dgl.DGLGraph((u, v)) G = build_karate_club_graph() print('We have %d nodes.' % G.number_of_nodes()) print('We have %d edges.' % G.number_of_edges()) - 输出结果:
We have 34 nodes. We have 156 edges.
02-22
饯行
- tqdm代码示例:
from tqdm import tqdm
def train(total, epoch):
pbar = tqdm(total=total, bar_format='{l_bar}{r_bar}', dynamic_ncols=True)
pbar.set_description('Epoch {}'.format(epoch))
for i in range(total):
fields = {
'loss': random.random(),
'accuracy': random.random(),
'recall': random.random(),
}
pbar.set_postfix(**fields)
pbar.update()
if __name__ == '__main__':
total = 1024
n_epoch = 16
for epoch in range(1, 1 + n_epoch):
train(total=total, epoch=epoch)
- 注意这种写法要求外循环体
for epoch in range(1, 1 + n_epoch)中不含有print的内容, 否则依然会输出很多行;
02-23
- 两点到宿舍,花了两个小时打扫卫生,安置物品,yjz先我一步已经回来。
- 总结下来这个寒假确实没做什么事情,完全没有动力,不过倒是一天也没惹老妈生气,陪家人做了很多事情,以后可能回来的机会越来越少了。
- 坚持了每天跑步(前三周周均60km,前30天总量204km,后期虽然腿伤,但也是至少每天4km的量在跑),半马或许还是只能是存在于梦想中的东西,看了一些过来人的经验,很多人无外乎如此,一失足成万古恨,不管你之前成绩多么好,能40分钟跑10km,膝盖报销就在一瞬间,现在不管以什么样的配速跑,5km就都是极限了,我也不知道自己还能不能回到之前的水平,现在虽然感觉不到膝盖疼痛,但是跑上2km就明显感觉腿不对劲了,或许以后只能每天慢慢跑个5圈10圈了罢,唉。
- 使用
datetime.datetime.fromtimestamp():
- 代码示例:
from datetime import datetime timestamp = 1381419600 print(datetime.fromtimestamp(timestamp))- 输出结果:
2013-10-10 23:40:00
- 输出结果:
- 注意:
- 该函数无keyword augments, 即不需要添加参数名称;
- 与
time.localtime()函数不同,datetime.datetime.fromtimestamp()接收的时间戳至少为86400, 前者则可以从0开始;
02-24
- 空想还是不如参考前人的做法,有时候还是不应该对自己胡扯的能力太过自信。
- pypdf2操作相关:合并pdf文件(详见本人blog,应无侵权行为)
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
import cv2
import numpy
from PyPDF2 import PdfFileReader, PdfFileWriter
def parse_pdf_images(import_path: str) -> None:
with open(import_path, 'rb') as pdf:
reader = PdfFileReader(pdf)
for number in range(reader.getNumPages()):
page = reader.getPage(number)
print('Page {}:'.format(number))
x_object = page['/Resources'].get('/XObject')
if x_object is None:
continue
for key in x_object:
if x_object[key]['/Subtype'] == '/Image':
size = (x_object[key]['/Width'], x_object[key]['/Height'])
data = x_object[key].getData()
if x_object[key]['/ColorSpace'] == '/DeviceRGB':
mode = 'RGB'
else:
mode = 'P'
image = numpy.frombuffer(data, numpy.uint8)
print(x_object[key]['/Filter'])
if x_object[key]['/Filter'] == '/FlateDecode':
print(size)
print(image.shape)
image = image.reshape(size[1], size[0], 3)
cv2.imwrite('page' + '%05ui' % number + 'key' + key[1:] + '.png', image)
elif x_object[key]['/Filter'] == '/DCTDecode':
cv2.imwrite(key[1:] + '.jpg', image)
elif xObject[obj]['/Filter'] == '/JPXDecode':
cv2.imwrite(key[1:] + '.jpg', image)
'''
try:
xObject = page['/Resources']['/XObject'].getObject()
except:
print(' - Fail ...')
continue
print(' - {}'.format(xObject))
for obj in xObject:
print(' - {}'.format(xObject[obj]['/Subtype']))
if xObject[obj]['/Subtype'] == '/Image':
size = (xObject[obj]['/Width'], xObject[obj]['/Height'])
data = xObject[obj].getData()
if xObject[obj]['/ColorSpace'] == '/DeviceRGB':
mode = 'RGB'
else:
mode = 'P'
if xObject[obj]['/Filter'] == '/FlateDecode':
img = np.fromstring(data, np.uint8)
img = img.reshape(size[1],size[0])
img = 255-img
img = img+1
img = img[:,220:-225]
cv2.imwrite("page"+"%05ui"%i+"obj"+obj[1:]+".png",img)
pic_list.append("page"+"%05ui"%i+"obj"+obj[1:]+".png")
elif xObject[obj]['/Filter'] == '/DCTDecode':
img = np.fromstring(data,np.uint8)
cv2.imwrite(obj[1:]+".jpg",img)
elif xObject[obj]['/Filter'] == '/JPXDecode':
img = np.fromstring(data,np.uint8)
cv2.imwrite(obj[1:]+".jp2",img)
'''
if __name__ == '__main__':
# format_reference_text(
# import_path=r'D:\study\paper\1906.08340_reference.md',
# export_path=r'D:\study\paper\1906.08340_reference_formatted.md',
# index_start_char='[',
# index_end_char=']',
# )
parse_pdf_images(
# import_path='1906.08340.pdf',
import_path=r'D:\code\python\project\paper\paper1_RE2RNN\emnlp20reg.pdf',
)
02-25
- 雨蒙蒙的一天,疯狂码字,但是真的感觉提不太起精神。下学期六门专业课,似乎是个巨大的挑战,但是转念一想每门课都和lth一起上,也是一件大幸事,高中同桌三年,本科四年未能在同一间教室里上过课,然而研究生阶段有这么一次同台竞技的机会,实然使人振奋得很。
- 跑了两天4km,感觉鞋有点问题,脚有些扭到了,如今4km跑起来都费事,但也要坚持下去。曾经26’38"的6km和45‘53“的10km,以及完全跑不累的71’08" 15km可能再也回不去了。
- python数组一些常用的工具函数:排序并记录排序前的索引值
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
from typing import List
def sorted_index(array: List[int]) -> (List[int], List[int]):
sorted_index_array = sorted(enumerate(array), key=lambda k: k[1])
sorted_index = [x[0] for x in sorted_index_array]
sorted_array = [x[1] for x in sorted_index_array]
return sorted_index, sorted_array
if __name__ == '__main__':
array = [1,3,5,7,9,2,4,6,8,10]
sorted_index, sorted_array = sorted_index(array)
print(sorted_index)
print(sorted_array)
02-26
- 元宵,连日阴雨,还要下几天,不适。
- 今晚换了日常穿的鞋去跑,结果4km配速4’38",前几天5分配都够呛。风停雨息,我觉得自己又行了,难道新买的跑鞋真的是坑,穿上就再也跑不快了,感觉是鞋底弹性太好每一步都变慢了。
- 最近在看自适应界面生成的问题,确实是个大坑,但是可能还非做不可。
- 这方面可能会涉及很久之前学过的一种叫做交互式机器学习的概念,印象中似乎和在线学习也有一定关联。
- 总之可以好好研究一下。
02-27
- 又多了一些新的思路,扩充了一下内容,差不多一万字了。
- 在
import tensorflow时触发警告: (tensorflow版本为2.3.0)
W tensorflow/stream_executor/platform/default/dso_loader.cc:59] Could not load dynamic library 'cudart64_101.dll'; dlerror: cudart64_101.dll not found
- 处理方案: 去路径
%CUDA_PATH%\bin下将cudart64_xxx.dll改为cudart64_101.dll即可;
- 原因: CUDA版本不匹配, 从警告内容可以看出
tensorflow 2.3.0对应的CUDA版本应为10.1, 笔者使用的为CUDA 10.2, 所以%CUDA_PATH%\bin路径下只有cudart64_102.dll, 一般高版本会兼容低版本, 所以直接改名即可, 低版本(如CUDA 10.0, 注意从tensorflow 2.0.0之后, 对CUDA版本的最低要求就是CUDA 10.0); - 关于CUDA版本对应问题最新更新的结果在https://tensorflow.google.cn/install/source_windows ;
02-28
- 就是鞋子的问题,我发现这个鞋子真的毒,穿上5圈就能把人跑废,弹性好确实保护关节,但是跑得也太累了,好奇怪啊。不过今天也是有点闷,不是很适合户外跑。
1.1 pipeline()方法
transformers.pipeline(task: str,
model: Optional = None,
config: Optional[Union[str, transformers.configuration_utils.PretrainedConfig]] = None,
tokenizer: Optional[Union[str, transformers.tokenization_utils.PreTrainedTokenizer]] = None,
framework: Optional[str] = None,
revision: Optional[str] = None,
use_fast: bool = True, **kwargs) → transformers.pipelines.base.Pipeline
- 参数说明:
task: 即管道适用的任务类型, 通过设置不同的task值将返回不同类型的管道对象;'feature-extraction': 返回FeatureExtractionPipeline;'sentiment-analysis': 返回TextClassificationPipeline;'ner': 返回TokenClassificationPipeline;'question-answering': 返回QuestionAnsweringPipeline;'fill-mask': 返回FillMaskPipeline;'summarization': 返回SummarizationPipeline;'translation_xx_to_yy': 返回TranslationPipeline;'text2text-generation': 返回Text2TextGenerationPipeline;'text-generation': 返回TextGenerationPipeline;'zero-shot-classification': 返回ZeroShotClassificationPipeline;'conversation': 返回ConversationalPipeline;
model: 即管道所使用的模型, 默认会从huggingface镜像中下载模型, 可以传入继承自PreTrainModel(PyTorch)或TFPreTrainModel(Tensorflow)的变量;config: 配置信息, 见transformers.PretrainedConfig
- 示例:
>>> from transformers import pipeline, AutoModelForTokenClassification, AutoTokenizer >>> # Sentiment analysis pipeline >>> pipeline('sentiment-analysis') >>> # Question answering pipeline, specifying the checkpoint identifier >>> pipeline('question-answering', model='distilbert-base-cased-distilled-squad', tokenizer='bert-base-cased') >>> # Named entity recognition pipeline, passing in a specific model and tokenizer >>> model = AutoModelForTokenClassification.from_pretrained("dbmdz/bert-large-cased-finetuned-conll03-english") >>> tokenizer = AutoTokenizer.from_pretrained("bert-base-cased") >>> pipeline('ner', model=model, tokenizer=tokenizer)
2021年3月
03-01
- 新的一个月,新的学期第一天,真是一个非常好的开始。
- 还是这种生活节奏畅快,上课,看代码,写报告。
- 下午与lth碰头,老朋友虽然数年没太多交流,但是一见面还是非常亲切的,这学期所有的课都将和lth一起上,也算是一件幸事了,至少不会辣么枯燥,而且有这家伙在,我想必也会充满斗志的,彼此干掉对方都是件快乐的事情。你我知根知底,就无需藏着掖着了。
- Transformers笔记:我最近在系统地看Transformers库地API文档,可能会更新一篇blog
- 任务类型:
- (1) 情感分析(Sentiment analysis): 判断文本是积极的或是消极的;
- (2) 文本生成(Text generation): 根据某种提示生成一段相关文本;
- (3) 命名实体识别(Name entity recognition): 判断语句中的某个分词属于何种类型;
- (4) 问答系统(Question answering): 根据上下文和问题生成答案;
- (5) 缺失文本填充(Filling masked text): 还原被挖去某些单词的语句;
- (6) 文本综述(Summarization): 根据长文本生成总结性的文字;
- (7) 机器翻译(Translation): 将某种语言的文本翻译成另一种语言;
- (8)特征挖掘(Feature extraction): 生成文本的张量表示;
- 以情感分析为例, 给出一个快速上手的示例:
from transformers import pipeline nlp = pipeline("sentiment-analysis") result = nlp("I hate you")[0] print(f"label: {result['label']}, with score: {round(result['score'], 4)}") result = nlp("I love you")[0] print(f"label: {result['label']}, with score: {round(result['score'], 4)}")- 该管道模型从distilbert-base-uncased-finetuned-sst-2-english 处下载获得, 如果需要指定使用哪种特定的模型, 可以设置
model参数, 获取从model hub 上储存的模型, 如下面这个模型除了可以处理英文外, 还可以处理法语, 意大利语, 荷兰语:
from transformers import pipeline classifier = pipeline('sentiment-analysis', model="nlptown/bert-base-multilingual-uncased-sentiment")- 关于这些模型的参数可以到huggingface页面上去查阅README文件;
- 通常可以为管道模型添加
tokenizer参数, 即指定好分词器, transformers库中已经提供了相应的模块AutoModelForSequenceClassification或TFAutoModelForSequenceClassification:# PyTorch from transformers import AutoTokenizer, AutoModelForSequenceClassification model_name = "nlptown/bert-base-multilingual-uncased-sentiment" model = AutoModelForSequenceClassification.from_pretrained(model_name) tokenizer = AutoTokenizer.from_pretrained(model_name) classifier = pipeline('sentiment-analysis', model=model, tokenizer=tokenizer) # TensorFlow from transformers import AutoTokenizer, TFAutoModelForSequenceClassification model_name = "nlptown/bert-base-multilingual-uncased-sentiment" # This model only exists in PyTorch, so we use the `from_pt` flag to import that model in TensorFlow. model = TFAutoModelForSequenceClassification.from_pretrained(model_name, from_pt=True) tokenizer = AutoTokenizer.from_pretrained(model_name) classifier = pipeline('sentiment-analysis', model=model, tokenizer=tokenizer)
- 如果需要在特定的数据集上微调这些预训练管道模型, 可以参考Example ;
- 该管道模型从distilbert-base-uncased-finetuned-sst-2-english 处下载获得, 如果需要指定使用哪种特定的模型, 可以设置
03-02
- 阴雨连绵一周后,终于放晴,可惜后天又要开始降雨,烦得很。
- 下午趁晴朗穿短裤去跑了一发,5.35km,均配4’39",第一个1km是4’56",后程速度倒还说得过去,感觉可能还是有机会能恢复到巅峰状态的,现在都是带着护膝跑了,虽然影响一些速度,但是至少要保住膝盖。
- 使用预训练模型: 经过分词器预处理后的数据可以直接输入到模型中, 正如上文所述, 分词器的输出包含了模型所需的所有信息:
- 示例: 注意PyTorch版本需要打包字典输入;
# PyTorch # import torch # pt_outputs = pt_model(**pt_batch, labels = torch.tensor([1, 0])) # add labels outputs = pt_model(**pt_batch) print(outputs) # TensorFlow # import tensorflow as tf # tf_outputs = tf_model(tf_batch, labels = tf.constant([1, 0])) # add labels outputs = tf_model(tf_batch) print(outputs)- 输出结果:
(tensor([[-4.0833, 4.3364], [ 0.0818, -0.0418]], grad_fn=<AddmmBackward>),) (<tf.Tensor: shape=(2, 2), dtype=float32, numpy= array([[-4.0832963 , 4.336414 ], [ 0.08181786, -0.04179301]], dtype=float32)>,)- 重点注意: 输出结果是去除了模型最后一个激活层(如
softmax等激活函数)的输出, 这在所有transformers库中的模型都是通用的, 原因是最后一个激活层会和损失函数相融合(fused with loss)
03-03
- 4km破18’00",近一个月来第一次跑回伤残前的水平。天晴了,雨停了,老子觉得自己又行了(半月板警告
- 我感觉王英林还是靠谱的,但是毕竟年纪大了,行动稍显迟缓,让我们这些年轻人实在是有些焦虑。
问答挖掘
- 关于SQuAD任务的模型微调可以参考run_squad.py 与run_tf_squad.py , 前者的PyTorch脚本似乎已经挂掉了, 只有后者TensorFlow的脚本仍然是有效的了;
- 简单示例一:
from transformers import pipeline nlp = pipeline("question-answering") context = r""" Extractive Question Answering is the task of extracting an answer from a text given a question. An example of a question answering dataset is the SQuAD dataset, which is entirely based on that task. If you would like to fine-tune a model on a SQuAD task, you may leverage the examples/question-answering/run_squad.py script. """ result = nlp(question="What is extractive question answering?", context=context) print(f"Answer: '{result['answer']}', score: {round(result['score'], 4)}, start: {result['start']}, end: {result['end']}") # Answer: 'the task of extracting an answer from a text given a question.', score: 0.6226, start: 34, end: 96 result = nlp(question="What is a good example of a question answering dataset?", context=context) print(f"Answer: '{result['answer']}', score: {round(result['score'], 4)}, start: {result['start']}, end: {result['end']}") # Answer: 'SQuAD dataset,', score: 0.5053, start: 147, end: 161
03-04
- 汝大逆不道,当死无赦。
- 以后博客更新频率恐怕会越来越低了,我总归也要逐渐放弃一些不再该做的事情了。
- 真的很想再回到以前的水平,我到现在都很难相信自己两个月前能跑38圈操场都不带喘,现在跑个5圈就逼近极限了。
- jupyter中调用parser.parse_args()报错
- 报错内容:
ipykernel_launcher.py: error: unrecognized arguments: -f /Users/apple/Library/Jupyter/runtime/kernel; - 解决方案: 使用
parser.parse_known_args()[0]替代parser.parse_args()即可;
03-05
- 下午午睡起来跑出4km的个人最好成绩,17’20",平均配速跑进4’20",最后1km用时3’58",爷的青春回来了。
- 这个月不打算跑15圈以上的里程,仍然以膝盖恢复为主线任务,我一定要恢复到巅峰状态。
- 至此,各项pb:12’58"(3km),17’20"(4km),26’38"(6km),45’53"(10km),71’08"(15km),腿废也值了。
- 查看pip安装库的时间及详细信息:
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
import os
import pandas
from datetime import datetime
from pip._internal.utils.misc import get_installed_distributions
from utils import *
class PipLogger(object):
def __init__(self) -> None:
self.logging_dict = {
'index': [],
'createdTime': [],
'modifiedTime': [],
'package': [],
}
def logging_pip_install_packages(self, export_path_csv:str=None, export_path_markdown: str=None) -> None:
packages = []
for package in get_installed_distributions():
package_metadata_path = os.path.dirname(package._get_metadata_path_for_display('RECORD'))
created_time = os.path.getctime(package_metadata_path)
modified_time = os.path.getmtime(package_metadata_path)
created_time = datetime.fromtimestamp(created_time)
modified_time = datetime.fromtimestamp(modified_time)
packages.append([created_time, modified_time, str(package)])
index = 0
for created_time, modified_time, package_name_version in sorted(packages):
index += 1
self.logging_dict['index'].append(index)
self.logging_dict['createdTime'].append(created_time)
self.logging_dict['modifiedTime'].append(modified_time)
self.logging_dict['package'].append(package_name_version)
logging_df = pandas.DataFrame(self.logging_dict, columns=list(self.logging_dict.keys()))
if export_path_csv is not None:
logging_df.to_csv(export_path_csv, header=True, index=False, sep='\t')
if export_path_csv is not None:
with open(export_path_markdown, 'w', encoding='UTF-8') as f:
f.write(pandas_dataframe_to_markdown_table(logging_df))
if __name__ == '__main__':
pip_logger = PipLogger()
pip_logger.logging_pip_install_packages(export_path_csv='pip.csv', export_path_markdown='pip.md')
03-06
- 抗衡周六魔咒失败,不过懒觉睡得是挺舒服的。
- 双腿感觉已经恢复了。不过阴沉的天气实在是让人打不起精神。
- 论文标题: Integrating Adaptive User Interface Capabilities in Enterprise Applications
- 中文标题: 在企业应用中集成用户界面自适应功能
- 免费下载链接: citeseerx
03-07
- 阴雨连绵,4’34"配4km
- 令人苦恼的任务,江郎才尽,黔驴技穷了
- paper参考文献修改
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
def format_reference_text(import_path: str, export_path: str=None, index_start_char: str='[', index_end_char: str=']') -> None:
"""
Format reference text copied from PDF file.
:param import_path : Import path of reference text file.
:param export_path : Export path of Formatted reference text file.
:param index_start_char : Starting char of reference entries' index.
:param index_end_char : Ending char of reference entries' index.
"""
if export_path is None:
export_path = 'formatted_{}'.format(import_path)
with open(import_path, 'r', encoding='utf8') as f:
lines = f.read().splitlines()
reference_index = 0
references = []
entry = None
for line in filter(None, lines):
line = line.strip()
if line.startswith(index_start_char):
reference_index += 1
if entry is not None:
references.append(''.join(entry))
entry = []
index = line.find(index_end_char)
prefix = '[{}] '.format(str(reference_index).zfill(2))
suffix = line[index + 1:]
else:
prefix = ''
suffix = line[:]
if suffix.endswith('-'):
entry.append(prefix + suffix[:-1].strip())
else:
entry.append(prefix + suffix + ' ')
with open(export_path, 'w', encoding='utf8') as f:
f.write('\n'.join(references))
if __name__ == '__main__':
'''
format_reference_text(
import_path=r'1.txt',
export_path=r'1.md',
index_start_char='[',
index_end_char=']',
)'''
parse_pdf_images(
import_path='1.pdf',
)
03-08
- 感觉状态不错,晚上去操场再试试,可惜碰上下雨,还是只跑了10圈,不过明显体力仍然很充沛,慢慢地状态开始起来了,稳一个月,别浪,下个月开始突破。
- 发现人的自律性就很奇怪,要始终保持自律是一件很难得事情,但是一旦自律起来真的很可怕;
- dgl的GCN demo
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from dgl import DGLGraph
from dgl.data import register_data_args, load_data
def gcn_msg(edges):
return {'m' : edges.src['h']}
def gcn_reduce(nodes):
return {'h' : torch.sum(nodes.mailbox['m'], 1)}
class NodeApplyModule(nn.Module): # define the GCN layer.
def __init__(self, in_feats, out_feats, activation=None):
super(NodeApplyModule, self).__init__()
self.linear = nn.Linear(in_feats, out_feats)
self.activation = activation
def forward(self, nodes):
# normalization by square root of dst degree
h = nodes.data['h']
h = self.linear(h)
if self.activation:
h = self.activation(h)
return {'h' : h}
03-09
- 无事发生,我回校快三个星期了,就出了三天太阳,我真的是吐了
- 稍微起了一些状态,有点等不及到月底了,准备中旬开始冲刺10km。
Greedy algorithm Max 算法证明(作业,感觉证的有点复杂,不知道对不对)
-
① 充分性证明:
命题:若 ( U , I ) (U,I) (U,I)构成一个拟阵,则对于任意成本函数 c ( ⋅ ) c(\cdot) c(⋅),通过Greedy Algorithm Max算法可以得出最优解。
不妨设成本函数值的排序结果为: c ( x 1 ) ≥ c ( x 2 ) ≥ . . . ≥ c ( x n ) > 0 x i ∈ U i = 1 , 2 , . . . , n c(x_1 )\ge c(x_2 )\ge...\ge c(x_n)>0\quad x_i\in U\quad i=1,2,...,n c(x1)≥c(x2)≥...≥c(xn)>0xi∈Ui=1,2,...,n;
-
假设通过Greedy Algorithm Max输出的解 A A A非最优解,那么一定存在一个最优解 A ∗ A^* A∗与集合 A A A的元素构成是不完全相同的,显然最优解满足 A ∗ ∈ I A^*\in I A∗∈I,我们分以下两种情况讨论:
-
情况一: A ∗ A^* A∗中的每个元素都属于集合 A A A,即 A ∗ ⊂ A A^*\subset A A∗⊂A且 ∣ A ∗ ∣ < ∣ A ∣ |A^*|\lt|A| ∣A∗∣<∣A∣;
显然此时 ( 1 ) (1) (1)式成立:
∑ x ∈ A ∗ c ( x ) < ∑ x ∈ A c ( x ) (1) \sum_{x\in A^*}c(x)<\sum_{x\in A}c(x)\tag{1} x∈A∗∑c(x)<x∈A∑c(x)(1)
与 A ∗ A^* A∗是最优解矛盾; -
情况二: A ∗ A^* A∗中至少存在一个不属于 A A A的元素,即 ∃ x ∈ A ∗ \exists x\in A^* ∃x∈A∗满足 x ∉ A x\notin A x∈/A,不妨设 x k x_k xk是满足这种性质的 x x x中下标值最小的,即 k k k的取值满足 ( 2 ) (2) (2)式的约束:
x i ∈ A ∩ A ∗ ∀ i = 1 , 2 , . . . , k − 1 x k ∈ A ∗ x k ∉ A (2) x_i\in A\cap A^*\quad\forall i=1,2,...,k-1\quad\\ x_k\in A^*\\ x_k\notin A\tag{2} xi∈A∩A∗∀i=1,2,...,k−1xk∈A∗xk∈/A(2)
考察在Greedy algorithm max算法流程中 x k x_k xk没有添加到集合 A A A中的原因:显然是因为在判断是否应当将 x k x_k xk添加到集合 A k A_k Ak中时,发现此时满足 A k ∪ { x k } ∉ I A_k\cup\{x_k\}\notin I Ak∪{xk}∈/I;( A k A_k Ak表示算法遍历到 x k x_k xk时集合 A A A的构成情况)
注意到算法遍历到 x k x_k xk时, A k A_k Ak中所包含的元素都在 A ∗ A^* A∗中(由 k k k是最小下标值的假设得出),即此时满足 A k ∈ A ∗ A_k\in A^* Ak∈A∗;
又由 ( 2 ) (2) (2)式知 x k ∈ A ∗ x_k\in A^* xk∈A∗,则有 A k ∪ { x k } ⊂ A ∗ A_k\cup\{x_k\}\subset A^* Ak∪{xk}⊂A∗;
又已知 A ∗ ∈ I A^*\in I A∗∈I,根据拟阵性质,则有 A k ∪ { x k } ∈ I A_k\cup\{x_k\}\in I Ak∪{xk}∈I;
这与 A k ∪ { x k } ∉ I A_k\cup\{x_k\}\notin I Ak∪{xk}∈/I矛盾;
-
-
综上所述,不存在一个最优解 A ∗ A^* A∗与集合 A A A的元素构成是不完全相同的,因此通过Greedy Algorithm Max算法输出的解 A A A为最优解,充分性得证。
-
-
② 必要性证明:
命题:若对于任意成本函数 c ( ⋅ ) c(\cdot) c(⋅),通过Greedy Algorithm Max算法可以得出最优解,则 ( U , I ) (U,I) (U,I)构成一个拟阵。
逆否命题:若 ( U , I ) (U,I) (U,I)不构成一个拟阵,则存在一个成本函数 c ( ⋅ ) c(\cdot) c(⋅),通过Greedy Algorithm Max算法无法得出最优解。
考察 ( U , I ) (U,I) (U,I)是否满足拟阵的三个性质:
( 1 ) (1)\quad (1) ∅ ∈ I \emptyset\in I ∅∈I;
( 2 ) (2)\quad (2)若 A ∈ I , B ⊂ A A\in I,B\subset A A∈I,B⊂A,则 B ∈ I B\in I B∈I;
( 3 ) (3)\quad (3)若 A ∈ I , B ∈ I , ∣ A ∣ > ∣ B ∣ A\in I,B\in I,|A|>|B| A∈I,B∈I,∣A∣>∣B∣,则 ∃ x ∈ A \exists x\in A ∃x∈A,使得 B ∪ { x } ∈ I B\cup\{x\}\in I B∪{x}∈I成立;
-
性质 ( 1 ) (1) (1):平凡,显然成立;
-
性质 ( 2 ) (2) (2):
考察必要性命题的逆否命题,即:
证明:若 ( U , I ) (U,I) (U,I)不满足性质 ( 2 ) (2) (2),则存在一个成本函数 c ( ⋅ ) c(\cdot) c(⋅),通过Greedy Algorithm Max算法无法得出最优解。
已知 ( U , I ) (U,I) (U,I)不满足性质 ( 2 ) (2) (2),即集合族 I I I中可以找到一个集合 A A A,至少存在一个 B ⊂ A B\subset A B⊂A,满足 B ∉ I B\notin I B∈/I;
令集合 S A S_A SA是集合族 I I I中包含元素最多的 A A A的超集(目的是使得集合族 I I I中不存在以 S A S_A SA为真子集的集合),即:
S A = a r g m a x S ∈ I ∣ S ∣ : A ⊆ S S A ⊂ S ⇒ S ∉ I (3) S_A = {\rm argmax}_{S\in I}|S|:A\subseteq S\tag{3}\\ S_A\subset S\Rightarrow S\notin I SA=argmaxS∈I∣S∣:A⊆SSA⊂S⇒S∈/I(3)
则有 B ⊂ S A B\subset S_A B⊂SA,我们说明可以构造出成本函数 c ( ⋅ ) c(\cdot) c(⋅),使得 S A S_A SA是唯一的最优解且通过Greedy Algorithm Max算法无法得出 S A S_A SA。-
首先,我们说明可以构造出非负成本函数 c ( ⋅ ) c(\cdot) c(⋅),使得 S A S_A SA是唯一的最优解:
设 S A = { x a 1 , x a 2 , . . . , x a p } S_A=\{x_{a_1},x_{a_2},...,x_{a_p}\} SA={xa1,xa2,...,xap},设在全集 U U U中 S A S_A SA的补集为 S A c = { x b 1 , x b 2 , . . . , x b q } S_A^c=\{x_{b_1},x_{b_2},...,x_{b_q}\} SAc={xb1,xb2,...,xbq};
不妨设 S A S_A SA中元素的成本函数呈降序排列: c ( x a 1 ) ≥ c ( x a 2 ) ≥ . . . ≥ c ( x a p ) c(x_{a_1})\ge c(x_{a_2})\ge...\ge c(x_{a_p}) c(xa1)≥c(xa2)≥...≥c(xap);
则除 S A S_A SA外,集合族 I I I中可能的成本函数之和最大的集合是 A ∗ = S A c ∪ { x a 1 , x a 2 , . . . , x a p − 1 } A^*=S_A^c\cup\{x_{a_1},x_{a_2},...,x_{a_{p-1}}\} A∗=SAc∪{xa1,xa2,...,xap−1};
注意到:
∑ x ∈ S A c ( x ) > ∑ x ∈ A ∗ c ( x ) ⇔ c ( x a p ) > ∑ x ∈ S A c c ( x ) (4) \sum_{x\in S_A}c(x)>\sum_{x\in A^*}c(x)\Leftrightarrow c(x_{a_p})>\sum_{x\in S_A^c}c(x)\tag{4} x∈SA∑c(x)>x∈A∗∑c(x)⇔c(xap)>x∈SAc∑c(x)(4)
即只需要构造 c ( x a p ) > ∑ x ∈ S A c c ( x ) c(x_{a_p})>\sum_{x\in S_A^c}c(x) c(xap)>∑x∈SAcc(x),即可使得 S A S_A SA是集合族 I I I中唯一的最优解; -
然后,我们说明在上述使得 S A S_A SA是唯一最优解的成本函数构造情况下(即 S A S_A SA中最小元素的成本函数值大于 S A S_A SA补集中所有元素的成本函数值之和),通过Greedy Algorithm Max算法无法得出 S A S_A SA。
同上我们假设 S A = { x a 1 , x a 2 , . . . , x a p } S_A=\{x_{a_1},x_{a_2},...,x_{a_p}\} SA={xa1,xa2,...,xap},全集 U U U中 S A S_A SA的补集为 S A c = { x b 1 , x b 2 , . . . , x b q } S_A^c=\{x_{b_1},x_{b_2},...,x_{b_q}\} SAc={xb1,xb2,...,xbq};
显然 ∀ 1 ≤ i ≤ q , 1 ≤ j ≤ p \forall 1\le i\le q,1\le j\le p ∀1≤i≤q,1≤j≤p,满足 c ( x a i ) > c ( x b j ) c(x_{a_i})>c(x_{b_j}) c(xai)>c(xbj),因此算法会先遍历 S A S_A SA中的元素;
已知 S A S_A SA中存在一个真子集 B B B,满足 B ∉ I B\notin I B∈/I,设 B = { x a b 1 , x a b 2 , . . . , x a b m } B=\{x_{a_{b_1}},x_{a_{b_2}},...,x_{a_{b_m}}\} B={xab1,xab2,...,xabm};
则只需要在构造 S A S_A SA中元素的成本函数时满足 c ( x a b 1 ) ≥ c ( x a b 2 ) ≥ . . . ≥ c ( x a b m ) c(x_{a_{b_1}})\ge c(x_{a_{b_2}})\ge...\ge c(x_{a_{b_m}}) c(xab1)≥c(xab2)≥...≥c(xabm),此时算法依次运行 x a b 1 , x a b 2 , . . . x a b m x_{a_{b_1}},x_{a_{b_2}},...x_{a_{b_m}} xab1,xab2,...xabm:
- 若算法运行到 x a b m x_{a_{b_m}} xabm时,候选最优解集包含了前面每一个元素,即为 { x a b 1 , x a b 2 , . . . , x a b m − 1 } \{x_{a_{b_1}},x_{a_{b_2}},...,x_{a_{b_m-1}}\} {xab1,xab2,...,xabm−1},那么 x a b m x_{a_{b_m}} xabm将无法添加到候选最优解集中,从而算法无法得到唯一的最优解 S A S_A SA;
- 若算法运行到 x a b m x_{a_{b_m}} xabm时,候选最优解集未能包含到前面的每一个元素,显然算法也无法得到唯一的最优解 S A S_A SA;
-
最后,综上所述, ( U , I ) (U,I) (U,I)满足性质 ( 2 ) (2) (2);
-
-
性质 ( 3 ) (3) (3):
考察必要性命题的逆否命题,即:
证明:若 ( U , I ) (U,I) (U,I)不满足性质 ( 3 ) (3) (3),则存在一个成本函数 c ( ⋅ ) c(\cdot) c(⋅),通过Greedy Algorithm Max算法无法得出最优解。
注意:此时可以假定 ( U , I ) (U,I) (U,I)已经满足性质 ( 2 ) (2) (2);
已知 ( U , I ) (U,I) (U,I)不满足性质 ( 3 ) (3) (3),即可以找到集合族 I I I中的一对集合 A A A和 B B B,满足 ∣ A ∣ > ∣ B ∣ |A|>|B| ∣A∣>∣B∣,则 ∀ x ∈ A \forall x\in A ∀x∈A,有 B ∪ { x } ∉ I B\cup\{x\}\notin I B∪{x}∈/I;
我们可以观察到集合 A A A和集合 B B B具有如下的性质:
-
显然集合 B B B非空,否则容易说明从集合 A A A中任取一个元素添加到集合 B B B中可以得到集合 A A A的一个子集,根据性质 ( 2 ) (2) (2),这与 B ∪ { x } ∉ I B\cup\{x\}\notin I B∪{x}∈/I的前提矛盾;
-
显然 B ∩ A = ∅ B\cap A=\emptyset B∩A=∅,否则从集合 A A A中取 x ∈ B ∩ A x\in B\cap A x∈B∩A,有 B ∪ { x } = B ∈ I B\cup\{x\}=B\in I B∪{x}=B∈I,从而推出与前提矛盾;
-
由集合 B B B非空与 ∣ A ∣ > ∣ B ∣ |A|>|B| ∣A∣>∣B∣,可知集合 A A A中至少包含两个元素,即 ∣ B ∣ ≥ 1 , ∣ A ∣ ≥ 2 |B|\ge 1,|A|\ge 2 ∣B∣≥1,∣A∣≥2;
令集合 S B S_B SB是集合族 I I I中包含元素最多的 B B B的超集(目的是使得集合族 I I I中不存在以 S B S_B SB为真子集的集合),即:
S B = a r g m a x S ∈ I ∣ S ∣ : B ⊆ S S B ⊂ S ⇒ S ∉ I (5) S_B = {\rm argmax}_{S\in I}|S|:B\subseteq S\tag{5}\\ S_B\subset S\Rightarrow S\notin I SB=argmaxS∈I∣S∣:B⊆SSB⊂S⇒S∈/I(5)
显然 S B ∩ A = ∅ S_B\cap A=\emptyset SB∩A=∅,否则从集合 A A A中取 x ∈ S B ∩ A x\in S_B\cap A x∈SB∩A添加到集合 B B B中,有 B ∪ { x } ⊂ S B ⇒ B ∪ { x } ∈ I B\cup\{x\}\subset S_B\Rightarrow B\cup\{x\}\in I B∪{x}⊂SB⇒B∪{x}∈I,从而推出与前提矛盾;于是集合 U U U的构成可以通过下图来表示:

为了简化表示,我们设
∣ U ∣ = n C = ( S B ∪ A ) c A = { x a 1 , x a 2 , . . . , x a p } B = { x b 1 , x b 2 , . . . , x b q } C = { x c 1 , x c 2 , . . . , x c r } S B = { x b 1 , x b 2 , . . . , x b Q } |U|=n\\ C=(S_B\cup A)^c\\ A=\{x_{a_1},x_{a_2},...,x_{a_p}\}\\ B=\{x_{b_1},x_{b_2},...,x_{b_q}\}\\ C=\{x_{c_1},x_{c_2},...,x_{c_r}\}\\ S_B=\{x_{b_1},x_{b_2},...,x_{b_Q}\} ∣U∣=nC=(SB∪A)cA={xa1,xa2,...,xap}B={xb1,xb2,...,xbq}C={xc1,xc2,...,xcr}SB={xb1,xb2,...,xbQ}
根据上述说明,我们有:
p + Q + r = n p ≥ 2 q ≥ 1 r ≥ 0 n ≥ 3 q ≤ Q q < p (6) p+Q+r=n\\ p\ge 2\\ q\ge 1\\ r\ge 0\\ n\ge 3\\ q\le Q\\ q\lt p\tag{6} p+Q+r=np≥2q≥1r≥0n≥3q≤Qq<p(6)
我们构造全集 U U U中元素的成本函数使其满足如下所有条件:- 构造条件一: S B S_B SB中元素的成本函数呈降序排列: c ( x b 1 ) ≥ c ( x b 2 ) ≥ . . . ≥ c ( x b Q ) c(x_{b_1})\ge c(x_{b_2})\ge...\ge c(x_{b_Q}) c(xb1)≥c(xb2)≥...≥c(xbQ);
- 构造条件二:集合 B = { x b 1 , x b 2 , . . . , x b q } B=\{x_{b_1},x_{b_2},...,x_{b_q}\} B={xb1,xb2,...,xbq}中共计 q q q个元素的成本函数值恰好是全集 U U U中前 q q q大的;确保算法会先遍历集合 B B B中的所有元素;
- 构造条件三:集合 A = { x a 1 , x a 2 , . . . , x a p } A=\{x_{a_1},x_{a_2},...,x_{a_p}\} A={xa1,xa2,...,xap}中共计 p p p个元素的成本函数值恰好是全集 U U U中第 ( q + 1 ) (q+1) (q+1)大到第 ( q + p ) (q+p) (q+p)大的;确保算法会遍历完集合 B B B中的所有元素后,紧接着遍历集合 A A A中的所有元素;
- 构造条件四:集合 C = { x c 1 , x c 2 , . . . , x c r } C=\{x_{c_1},x_{c_2},...,x_{c_r}\} C={xc1,xc2,...,xcr}中共计 r r r个元素的成本函数值恰好是全集 U U U中前 r r r小的;确保算法会最后遍历集合 C C C中的所有元素;
- 构造条件五: ∑ x ∈ A c ( x ) > ∑ x ∈ S B c ( x ) \sum_{x\in A}c(x)>\sum_{x\in S_B}c(x) ∑x∈Ac(x)>∑x∈SBc(x),即集合 A A A中所有元素的成本函数值之和大于集合 S B S_B SB中所有元素的成本函数值之和;确保集合 S B S_B SB不是最优解;
为了说明这五个构造条件可以被同时满足的,试根据式 ( 6 ) (6) (6)中的约束,给出一种成本函数构造的通式(如式 ( 7 ) (7) (7)所示,容易验证它满足上述五个构造条件):
c ( x b 1 ) = c ( x b 2 ) = . . . c ( x b q ) = p n c ( x a 1 ) = c ( x a 2 ) = . . . = c ( x a p ) = p + q 2 n c ( x b q + 1 ) = c ( x b q + 2 ) = . . . = c ( x b Q ) = 1 Q c ( x c 1 ) = c ( x c 2 ) = . . . = c ( x c r ) = 1 Q + 1 (7) c(x_{b_1})=c(x_{b_2})=...c(x_{b_q})=pn\\ c(x_{a_1})=c(x_{a_2})=...=c(x_{a_p})=\frac{p+q}{2}n\\ c(x_{b_{q+1}})=c(x_{b_{q+2}})=...=c(x_{b_Q})=\frac{1}{Q}\\ c(x_{c_1})=c(x_{c_2})=...=c(x_{c_r})=\frac{1}{Q+1}\tag{7} c(xb1)=c(xb2)=...c(xbq)=pnc(xa1)=c(xa2)=...=c(xap)=2p+qnc(xbq+1)=c(xbq+2)=...=c(xbQ)=Q1c(xc1)=c(xc2)=...=c(xcr)=Q+11(7)此时考察在该构造条件下Greedy Algorithm Max算法的运行情况:
- 首先算法会遍历集合 B B B中的所有元素,并将它们都加入到最优解候选集中;
- 接着算法会遍历集合 A A A中的所有元素,并且不会将任何一个元素加入到最优解候选集中;原因是 ∀ x ∈ A \forall x\in A ∀x∈A,有 B ∪ { x } ∉ I B\cup\{x\}\notin I B∪{x}∈/I;
- 然后算法会遍历集合 S B S_B SB中不属于集合 B B B的部分,即 { x b q + 1 , x b q + 2 , . . . , x b Q } \{x_{b_{q+1}},x_{b_{q+2}},...,x_{b_Q}\} {xbq+1,xbq+2,...,xbQ},并会将它们都加入到最优解候选集中;原因是 S B ∈ I ⇒ ∀ 1 ≤ t ≤ ( Q − q ) , B ∪ { x b q + t } ∈ I S_B\in I\Rightarrow\forall 1\le t\le(Q-q),B\cup\{x_{b_{q+t}}\}\in I SB∈I⇒∀1≤t≤(Q−q),B∪{xbq+t}∈I;
- 最后算法会遍历集合 C C C中的所有元素,并且不会将任何一个元素加入到最优解候选集中;原因是 S B S_B SB已经是集合族 I I I中集合 B B B最大的超集,不管向 S B S_B SB中加入任何其他元素都不能使其属于集合族 I I I了;
综上所述,Greedy Algorithm Max算法的输出结果就是 S B S_B SB,根据构造条件五, S B S_B SB不是最优解,因此算法无法得出最优解,因此 ( U , I ) (U,I) (U,I)满足性质 ( 3 ) (3) (3);
-
-
03-10
- 给hy寄了封成绩单到HKU,班到底还是不如学好上的;
- 挑灯夜战,感觉最近精神很好,但是一上操场就不行了;
- 难得的好天气,我翻了翻lth的票圈,发现确实是和zsj在一起,快乐也不过如此吧;
- Kruskal算法:
# -*- coding: UTF-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
def kruskal(nodes, edges):
_nodes = nodes.copy()
used_nodes = set()
MST = []
distance = 0
edges = sorted(edges, key=lambda x: x[2], reverse=True)
while edges and used_nodes != _nodes:
element = edges.pop(-1)
if element[0] in used_nodes and element[1] in used_nodes:
continue
MST.append(element)
used_nodes.update(element[:2])
distance += element[2]
return distance
if __name__ == '__main__':
"""
Sample inputs:
9
A 2 B 12 I 25
B 3 C 10 H 40 I 8
C 2 D 18 G 55
D 1 E 44
E 2 F 60 G 38
F 0
G 1 H 35
H 1 I 35
3
A 2 B 10 C 40
B 1 C 20
0
"""
outputs = []
n_nodes = int(input())
while True:
if n_nodes == 0:
break
nodes = set()
edges = []
while True:
inputs = input().split()
if len(inputs) == 1:
if n_nodes == len(nodes):
outputs.append(kruskal(nodes, edges))
else:
outputs.append(False)
n_nodes = int(inputs[0])
break
nodes.add(inputs[0])
for i in range(int(inputs[1])):
nodes.add(inputs[2 * i + 2])
edges.append([inputs[0], inputs[2 * i + 2], int(inputs[2 * i + 3])])
for output in outputs:
print(output)
03-11
- 感觉自己快要疯了,昨晚肝到十二点改申请书,今天wyl又打了几页的批注要改,真的是顶不住了,还有晚课要上。
- 集合的内点, 极限点, 边界:
- (1) 内点: 以内点为圆心画一个半径足够小圆可以包含在集合内部;
- (2) 极限点: 存在一个点列可以逼近到这个点;
- (3) 边界: 极限点 - 内点
- 如 [ 0 , 1 ] [0,1] [0,1]上所有无理数构成的点的内点是空集, 极限点是全集, 边界也是全集;
- i n t ( X ) ⊆ X ⊆ c l ( X ) {\rm int}(X)\subseteq X\subseteq {\rm cl}(X) int(X)⊆X⊆cl(X)
- X X X为开集: i n t ( X ) = X {\rm int}(X)=X int(X)=X, 注意无界的闭集同时也是开集
- X X X为闭集: c l ( X ) = X {\rm cl}(X)=X cl(X)=X
- 任意闭集的交仍是闭集, 有限闭集的并仍是闭集(无限多的话就可以构造出一个收敛序列了);
- 有限开集交仍为开集,任意开集的并仍为开集
- 思考: 若 X 1 , X 2 X_1,X_2 X1,X2是闭集, 则 X 1 + X 2 = { a + b : a ∈ X 1 , b ∈ X 2 } X_1+X_2=\{a+b:a\in X_1,b\in X_2\} X1+X2={a+b:a∈X1,b∈X2}是否为闭集?(不一定,如 { n + 1 n , n = 2 , 3 , 4... } \{n+\frac{1}{n}, n=2,3,4...\} {n+n1,n=2,3,4...}与整数集的加和就不是闭集, 因为2是聚点, 但是无法到达)
03-12
- 植树节,苦逼地还在改申请书,今晚不上课,于是这周连休三天;
- 凸函数:
-
定义: 定义域是 R n \mathbb{R}^n Rn上的凸集, 且满足 f ( α x 1 + ( 1 − α ) x 2 ) ≤ α f ( x 1 ) + ( 1 − α ) f ( x 2 ) f(\alpha x_1+(1-\alpha)x_2)\le\alpha f(x_1)+(1-\alpha)f(x_2) f(αx1+(1−α)x2)≤αf(x1)+(1−α)f(x2)
-
性质: 凸函数的局部最小点就是全局最小点;
-
严格凸: 定义中的 ≤ \le ≤改为 < \lt <, 严格凸函数只会有一个全局最优点;
-
常见的凸函数:
- a x + b , a , b ∈ R ax+b,a,b\in \mathbb{R} ax+b,a,b∈R, 线性函数同时也是凹方程;
- e a x , a ∈ R e^{ax},a\in \mathbb{R} eax,a∈R
- x p , p ∈ ( − ∞ , 0 ] ∪ [ 1 , + ∞ ) x^p,p\in(-\infty,0]\cup[1,+\infty) xp,p∈(−∞,0]∪[1,+∞)
- ∣ x ∣ p , p ≥ 1 |x|^p,p\ge 1 ∣x∣p,p≥1
- x log x x\log x xlogx
- R n \mathbb{R^n} Rn上的n阶模( n ≥ 1 n\ge 1 n≥1)与线性函数都是凸的;
-
R
m
×
n
\mathbb{R^{m×n}}
Rm×n上:
- f ( X ) = t r ( A ⊤ X + b = ∑ i = 1 m ∑ j = 1 n a i j x i j + b f(X)=tr(A^\top X+b=\sum_{i=1}^m\sum_{j=1}^na_{ij}x_{ij}+b f(X)=tr(A⊤X+b=∑i=1m∑j=1naijxij+b
- Spectral(maximum singular value) norm: f ( X ) = ∥ X ∥ 2 = σ max ( X ) = λ max ( X ⊤ X ) f(X)=\left\|X\right\|_2=\sigma_{\max}(X)=\sqrt{\lambda_{\max}(X^\top X)} f(X)=∥X∥2=σmax(X)=λmax(X⊤X),其中 λ max ( A ) \lambda_{\max}(A) λmax(A)表示矩阵 A A A的最大特征值;
03-13
- 最后一日,申请书DDL;我吐了;
- 想要明天跑个大的
- 我必须吐槽郭佳熠居然布置12道题,有几道还是大题有三四问,TMD都研究生了还做这么多作业,陆品燕才给了2道证明+2道code;昨天从中午一直写到晚上十二点才搞完,果然DDL是第一生产力。
-
保持凸性的操作:
-
凸函数乘以一个系数
-
若干凸函数加和
-
f ( x ) f(x) f(x)与仿射函数复合: f ( A x + b ) f(Ax+b) f(Ax+b);
-
f ( x ) = − ∑ i = 1 m log ( b i − a i ⊤ x ) , d o m ( f ) = { x ∣ a i ⊤ x < b i , i = 1 , 2 , . . , m } f(x)=-\sum_{i=1}^m\log(b_i-a_i^\top x),{\rm dom}(f)=\{x|a_i^\top x<b_i,i=1,2,..,m\} f(x)=−∑i=1mlog(bi−ai⊤x),dom(f)={x∣ai⊤x<bi,i=1,2,..,m}
- 关于证明:只考虑累和中的一项, ∂ f ∂ x 1 = a i b − a ⊤ x \frac{\partial f}{\partial x_1}=\frac{a_i}{b-a^\top x} ∂x1∂f=b−a⊤xai, ∂ 2 f ∂ x i ∂ x j = a i a j ( b − a ⊤ x ) 2 \frac{\partial^2f}{\partial x_i\partial x_j}=\frac{a_ia_j}{(b-a^\top x)^2} ∂xi∂xj∂2f=(b−a⊤x)2aiaj,可以发现Hessian矩阵是一个外积矩阵,必然半正定,得证;
-
f ( x ) = ∥ A x + b ∥ f(x)=\|Ax+b\| f(x)=∥Ax+b∥
-
-
Pointwise maximum:一组凸函数 f 1 , . . . , f m f_1,...,f_m f1,...,fm,则 F ( x ) = max { f 1 ( x ) , . . . , f m ( x ) } F(x)=\max\{f_1(x),...,f_m(x)\} F(x)=max{f1(x),...,fm(x)}是凸的,证明可以用定义,或使用epigraph的方法;
- 举例:一组仿射函数取最大;取一个向量前 k k k大的元素累和
-
Pointwise Supremum: g ( x ) = sup z ∈ A f ( x , z ) , A ⊆ R p , f : R n × p → R g(x)=\sup_{z\in\mathcal{A}}f(x,z),\mathcal{A}\subseteq R^p,f:\mathbb{R}^n×\mathbb{p}\rightarrow \mathbb{R} g(x)=supz∈Af(x,z),A⊆Rp,f:Rn×p→R,若 f ( x , z ) f(x,z) f(x,z)关于 x x x凸,对于每个 z ∈ A z\in\mathcal{A} z∈A成立,则 g ( x ) g(x) g(x)是凸的;
-
证明思路:考察 g ( α x 1 + ( 1 − α ) x 2 ) g(\alpha x_1+(1-\alpha)x_2) g(αx1+(1−α)x2)是否满足定义;
-
举例:
-
支撑集函数凸: C ⊂ R n C\subset \mathbb{R}^n C⊂Rn
s c : R n → R , S C ( x ) = sup z ∈ C z ⊤ x s_c:\mathbb{R}^n\rightarrow\mathbb{R},S_C(x)=\sup_{z\in C}z^\top x sc:Rn→R,SC(x)=supz∈Cz⊤x
-
f ( x ) = sup z ∈ C ∥ x − z ∥ f(x)=\sup_{z\in C}\|x-z\| f(x)=supz∈C∥x−z∥
-
λ max : S n → R \lambda_{\max}: \mathcal{S}^n\rightarrow\mathbb{R} λmax:Sn→R, λ max ( X ) = sup ∥ z ∥ = 1 z ⊤ X z \lambda_{\max}(X)=\sup_{\|z\|=1}z^\top Xz λmax(X)=sup∥z∥=1z⊤Xz,注意这里只要求 X X X是对称,而非正定,因为这个函数是定义在 X X X上的,如果定义在 z z z上需要 X X X正定,这里定义在 X X X上只要对称就凸了。
-
-
-
与标量函数复合: f ( x ) = h ( g ( x ) ) f(x)=h(g(x)) f(x)=h(g(x)),则 f ( x ) f(x) f(x)是凸的,若:
- g g g是凸的, h h h不减且凸;
- g g g是凹的, h h h不增且凸;
如 e g ( x ) e^{g(x)} eg(x)凸,若 g g g凸; 1 g ( x ) \frac{1}{g(x)} g(x)1凸,若 g g g凹且正;
- 证明: f ′ ( x ) = ∇ h ⊤ ( g ( x ) ) g ′ ( x ) , f ′ ′ ( x ) = g ′ ( x ) ⊤ ∇ 2 h ( g ( x ) ) g ′ ( x ) + ∇ h ⊤ ( g ( x ) ) g ′ ′ ( x ) ≥ 0 f^\prime(x)=\nabla h^\top(g(x))g^\prime(x),f^{\prime\prime}(x)=g^{\prime}(x)^\top\nabla^2h(g(x))g^\prime(x)+\nabla h^\top(g(x))g^{\prime\prime}(x)\ge 0 f′(x)=∇h⊤(g(x))g′(x),f′′(x)=g′(x)⊤∇2h(g(x))g′(x)+∇h⊤(g(x))g′′(x)≥0;
-
Minimization:与 sup \sup sup的证明类似,留作作业;
f f f凸,可以推出 g ( x ) = inf z ∈ C f ( x , z ) g(x)=\inf_{z\in C}f(x,z) g(x)=infz∈Cf(x,z)凸;
-
03-14
- 恐怕真的不行了,现在还是卡死在4km,腿坚持不了更长的距离了。
- 好痛苦的感觉;
-
如何验证函数的凸性:
-
定义法:用 1 2 \frac{1}{2} 21替代 α \alpha α证明即可;
-
使用特殊的标准:
-
一阶条件:可微函数 f f f是凸的,当且仅当其定义域是凸的,并且 f ( x ) + ∇ f ( x ) ⊤ ( y − x ) ≤ f ( y ) , ∀ x , y ∈ d o m ( f ) f(x)+\nabla f(x)^\top (y-x)\le f(y),\forall x,y\in {\rm dom}(f) f(x)+∇f(x)⊤(y−x)≤f(y),∀x,y∈dom(f),其中 ∇ f ( x ) = ( ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , . . . , ∂ f ( x ) ∂ x n ) \nabla f(x)=\left(\frac{\partial f(x)}{\partial x_1},\frac{\partial f(x)}{\partial x_2},...,\frac{\partial f(x)}{\partial x_n}\right) ∇f(x)=(∂x1∂f(x),∂x2∂f(x),...,∂xn∂f(x));本质是切线在函数图像下方;
- 关于证明:略,两个方向;一阶推凸非常简单,在切点左右各找一个点即可证明琴生(几何性质);凸推一阶需要一些微分技巧,构造 g ( t ) = f ( t y + ( 1 − t ) x ) g(t)=f(ty+(1-t)x) g(t)=f(ty+(1−t)x),也必然是一个凸函数(restrict convex function to a line),考察 g ′ ( t ) = ∇ f ( t y + ( 1 − t ) x ) ⊤ y − ∇ f ( t y + ( 1 − t ) x ) ⊤ x = ∇ f ( t y + ( 1 − t ) x ) ⊤ ( y − x ) g^\prime(t)=\nabla f(ty+(1-t)x)^\top y-\nabla f(ty+(1-t)x)^\top x=\nabla f(ty+(1-t)x)^\top(y-x) g′(t)=∇f(ty+(1−t)x)⊤y−∇f(ty+(1−t)x)⊤x=∇f(ty+(1−t)x)⊤(y−x),带入 g ( 1 ) g(1) g(1)和 g ( 0 ) g(0) g(0)即可,因为 g ( 1 ) − g ( 0 ) ≥ g ′ ( 0 ) ⋅ 1 g(1)-g(0)\ge g^{\prime}(0)\cdot 1 g(1)−g(0)≥g′(0)⋅1;
- 推论:若 ∇ f ( x ) ⊤ = 0 \nabla f(x)^\top=0 ∇f(x)⊤=0,则此处为全局最小点;
-
二阶条件:Hessian矩阵 ∇ 2 f ( x ) \nabla^2f(x) ∇2f(x)半正定等价于凸;正定等价于严格凸, ∀ x ∈ d o m ( f ) \forall x\in{\rm dom(f)} ∀x∈dom(f);
-
Taylor展开: f ( y ) = f ( x ) + ∇ f ⊤ ( x ) ( y − x ) + 1 2 ( y − x ) ⊤ ∇ 2 f ( x ^ ) ( y − x ) f(y)=f(x)+\nabla f^\top (x)(y-x)+\frac{1}{2}(y-x)^\top \nabla^2f(\hat x)(y-x) f(y)=f(x)+∇f⊤(x)(y−x)+21(y−x)⊤∇2f(x^)(y−x);
显然若已经有Hession矩阵(半)正定,最后一项(非负)恒正,命题退化为一阶条件;
若已经有凸性,即有一阶条件,则移项知最后一项(非负)恒正,则根据正定的定义也有二阶条件满足;
-
考察: f ( x 1 , x 2 ) = x 1 2 + 4 x 1 x 2 + x 2 2 f(x_1,x_2)=x_1^2+4x_1x_2+x_2^2 f(x1,x2)=x12+4x1x2+x22,它不是凸函数,但是如果分别固定 x 1 x_1 x1与 x 2 x_2 x2,得到的规约函数是凸的,这说明在 x 1 x_1 x1与 x 2 x_2 x2的方向上它是凸的,但是凸函数一定要对 x 1 x_1 x1与 x 2 x_2 x2组合的任意一个方向是凸的;
-
一些举例:
- Quadratic function: 1 2 x ⊤ P x + q ⊤ x + r \frac{1}{2}x^\top Px+q^\top x+r 21x⊤Px+q⊤x+r
- Least-squares objective: ∥ A x − b ∥ 2 \|Ax-b\|^2 ∥Ax−b∥2
- Quadratic over linear: x 2 y , y > 0 \frac{x^2}{y},y>0 yx2,y>0
-
-
规约(reduce)到一个标量(scalar)函数: f f f凸等价于存在一个函数 g : R → R g:\mathbb{R}\rightarrow\mathbb{R} g:R→R, g ( t ) = f ( x + t v ) g(t)=f(x+tv) g(t)=f(x+tv)是凸的, ∀ x ∈ d o m ( f ) , v ∈ R n \forall x\in {\rm dom}(f),v\in\mathbb{R}^n ∀x∈dom(f),v∈Rn;
-
-
03-15
- 抽搐了两天,还是跑不过10圈,看来我的跑步生涯到此为止了。
-
线性规划的标准型:
min c ⊤ x s . t . A x = b x ≥ 0 \min c^\top x\quad s.t.\\ Ax=b\\ x\ge 0 minc⊤xs.t.Ax=bx≥0- 对于可能有负值得变量可以替换为 x + + x − x^++x^- x++x−;
- a ⊤ x ≤ b ⇔ a ⊤ x + s = b , s ≥ 0 a^\top x\le b\Leftrightarrow a^\top x+s=b,s\ge 0 a⊤x≤b⇔a⊤x+s=b,s≥0
- x ≤ 3 ⇔ x + s = 3 , s ≥ 0 x\le 3\Leftrightarrow x+s=3,s\ge 0 x≤3⇔x+s=3,s≥0
- x ≥ 3 ⇔ x : = x − 3 x\ge 3\Leftrightarrow x:=x-3 x≥3⇔x:=x−3
03-16
- 也许结束了吧,开始看property testing,老大难了。
- 右膝盖头疼,不知是怎么回事。
-
什么是属性检验(property testing,下简称为PT):
-
关于大数据的全局属性的分析: 如确定数据整体是否具有某种全局属性(global property),或对数据结构中的全局参数进行估计;
-
大数据通常可以由图(graph)的形式建模,因为数据对象之间往往都会具有一定联系,挖掘由大数据建模得到的图中的自然属性(natural properties)是PT的研究内容之一;
-
注意图中的节点也可以是抽象的函数(function):如对象通过函数建模,则函数之间的距离可以由函数不同的域的分数来度量, 如果函数与具有该属性的任何函数的距离超过给定的近似参数(proximity parameter),则认为该函数不具有该属性;对这些函数性质的测试也属于PT的研究范畴,如函数是否为低阶的多项式(low degree polynomial),是否单调(monotone)等;
… and distance between functions is measured as the fraction of the domain on which the functions differ.
-
一些其他的PT研究范畴包括判断图是否二分(bipartite),是否不存在三角形(triangle-free),针对虚拟图片(visual images)或几何对象(geometric objects)的聚类性质(well-clustered)或凸性进行测试;
-
-
PT旨在挖掘超快算法,而避免获得对象的完整显式描述。
We refer to the fact that property testing seeks super-fast algorithms that refrain from obtaining the full explicit description of the object.
-
-
一些下文即将用到的符号表示说明:
- ∀ n ∈ N \forall n\in \mathbb{N} ∀n∈N,定义 [ n ] = d e f { 1 , 2 , . . . , n } [n]\overset{\rm def}{=}\{1,2,...,n\} [n]=def{1,2,...,n};
- 若 x x x为零一字符串,即 x ∈ { 0 , 1 } ∗ x\in\{0,1\}^* x∈{0,1}∗,则 ∣ x ∣ |x| ∣x∣表示 x x x的长度, x i x_i xi表示 x x x的第 i i i位的字节;
- 设 w t ( x ) = ∣ { i ∈ [ ∣ x ∣ ] : x i = 1 } ∣ = ∑ i = 1 ∣ x ∣ x i {\rm wt}(x)=|\{i\in[|x|]:x_i=1\}|=\sum_{i=1}^{|x|}x_i wt(x)=∣{i∈[∣x∣]:xi=1}∣=∑i=1∣x∣xi表示字符串 x x x的汉明权重(Hamming weight);
03-17
- 整整一天都被困在wyl处,早八到晚十一,总算终稿了。
- 肝了一天,我觉得应该结束了吧;
- “我不要你觉得,我要我觉得”
- 在计算机中浮点数表示方法为二进制小数: f = ∑ i = 1 d b i 2 − i , b i ∈ { 0 , 1 } f=\sum_{i=1}^db_i2^{-i},b_i\in\{0,1\} f=∑i=1dbi2−i,bi∈{0,1}
- round-off error: 近似后的绝对误差 ∣ f l o a t ( x ) − x ∣ |{\rm float}(x)-x| ∣float(x)−x∣, 这个数值的大小与浮点数的大小关系较大;
- relative round-off error: 近似后的误差率
∣
f
l
o
a
t
(
x
)
−
x
∣
∣
x
∣
\frac{|{\rm float}(x)-x|}{|x|}
∣x∣∣float(x)−x∣, 这个数值的大小与浮点数的大小关系不大;
- f l o a t ( x ) {\rm float}(x) float(x)是直接舍掉溢出的小数位的近似方法, 其实就是: f l o a t ( x ) = a r g m i n y ∣ x − y ∣ {\rm float}(x)={\rm argmin_y}|x-y| float(x)=argminy∣x−y∣
- 总之 f l o a t ( x ) = x ( 1 + ϵ ) {\rm float}(x)=x(1+\epsilon) float(x)=x(1+ϵ), 其中 ∣ ϵ ∣ ≤ 1 2 ϵ M = 2 − d − 1 |\epsilon|\le\frac{1}{2}\epsilon_M=2^{-d-1} ∣ϵ∣≤21ϵM=2−d−1, 其中 d d d是浮点数所能精确到的二进制小数的位数;
- IEEE标准: 浮点数存储在
(
1
+
d
+
k
)
(1+d+k)
(1+d+k)长度的数组中:
[
s
,
e
1
,
e
2
,
.
.
.
,
e
k
,
f
1
,
.
.
.
,
f
d
]
[s,e_1,e_2,...,e_k,f_1,...,f_d]
[s,e1,e2,...,ek,f1,...,fd], 其中
s
s
s是符号位(表示正负号), 一般
d
=
52
,
k
=
11
d=52,k=11
d=52,k=11, 总长度为
64
64
64;
- ① 若 e i e_i ei都等于0, 那么浮点数值为 ( − 1 ) s ( 0. f 1 f 2 . . . f 52 ) 2 ⋅ 2 − 1022 (-1)^s(0.f_1f_2...f_{52})_2\cdot2^{-1022} (−1)s(0.f1f2...f52)2⋅2−1022
- ② 若 e i e_i ei都等于1且 f j f_j fj都等于0, 那么浮点数值为 ( − 1 ) s ⋅ ∞ (-1)^s\cdot\infty (−1)s⋅∞
- ③ 若 e i e_i ei都等于1且 f j f_j fj不全为0, 那么浮点数值为 n a n \rm nan nan
- ④ 其他情况下, 浮点数为 ( − 1 ) s ( 1. f 1 f 2 . . . f 52 ) 2 ⋅ 2 ( e 1 e 2 . . . e 11 ) 2 − 1023 (-1)^s(1.f_1f_2...f_{52})_2\cdot2^{(e_1e_2...e_{11})_2-1023} (−1)s(1.f1f2...f52)2⋅2(e1e2...e11)2−1023
- 可以发现第①类中绝对值最大的数比 2 − 1022 2^{-1022} 2−1022略小一点点, 而 ± 2 − 1022 \pm 2^{-1022} ±2−1022恰好是第①类数的左右边界, 第④类数是规范数, 它们的范围是 ( − ∞ , − 2 − 1022 ] ∪ [ 2 − 1022 , + ∞ ) (-\infty,-2^{-1022}]\cup[2^{-1022},+\infty) (−∞,−2−1022]∪[2−1022,+∞)
- 且距离原点越近, 浮点数的密度越大; 距离远点越远, 浮点数密度越小; 因此应当在数轴上比较密的地方进行运算, 这样绝对误差会较小;
03-18
- 体能越来越差了。状态也一直不是很好。
令
x
~
=
f
l
o
a
t
(
x
)
=
x
(
1
+
ϵ
)
\tilde x={\rm float}(x)=x(1+\epsilon)
x~=float(x)=x(1+ϵ), 考察如下的统计量:
r
(
x
)
=
∣
f
(
x
)
−
f
(
x
~
)
∣
/
∣
f
(
x
)
∣
∣
x
~
−
x
∣
/
x
r(x)=\frac{|f(x)-f(\tilde x)|/|f(x)|}{|\tilde x-x|/x}
r(x)=∣x~−x∣/x∣f(x)−f(x~)∣/∣f(x)∣
根据泰勒展开有
f
(
x
~
)
≈
f
(
x
)
+
ϵ
f
′
(
x
)
x
f(\tilde x)\approx f(x)+\epsilon f^{\prime}(x)x
f(x~)≈f(x)+ϵf′(x)x, 则有近似的表达:
r
(
x
)
≈
ϵ
∣
f
′
(
x
)
x
∣
ϵ
∣
f
(
x
)
∣
=
∣
f
′
(
x
)
x
∣
∣
f
(
x
)
∣
=
κ
f
(
x
)
r(x)\approx\frac{\epsilon|f^\prime(x)x|}{\epsilon|f(x)|}=\frac{|f^\prime(x)x|}{|f(x)|}=\kappa_f(x)
r(x)≈ϵ∣f(x)∣ϵ∣f′(x)x∣=∣f(x)∣∣f′(x)x∣=κf(x)
其中
κ
f
(
x
)
\kappa_f(x)
κf(x)称为问题
f
(
x
)
f(x)
f(x)的条件数(condition number), 注意到如果
∣
f
′
(
x
)
∣
|f^\prime(x)|
∣f′(x)∣过大, 而
∣
f
(
x
)
∣
|f(x)|
∣f(x)∣过小, 那么输出就会被输入的微小扰动会有极大的改变; 即条件数越大, 可能的相对误差就越大;
- 一个非常简单的示例: 令 f ( x ) = x − 1 f(x)=x-1 f(x)=x−1, 设 x = 1 + e p s / 2 x=1+{\rm eps}/2 x=1+eps/2, 则输出为严格的 0 0 0;
- 如果计算 1 + ( e p s / 2 − 1 ) 1+({\rm eps}/2-1) 1+(eps/2−1), 那么将会得到 1.1102 e − 16 1.1102e-16 1.1102e−16;
- 原因是 1 1 1太大了, 附近的浮点数密度太低, 因此 1 + e p s / 2 1+{\rm eps}/2 1+eps/2中被加上的部分被约掉了, 而比1小的部分浮点数密度相对高一些, 所以 e p s / 2 − 1 {\rm eps}/2-1 eps/2−1中没有被约掉, 所以得出了正常的结果;
- 条件数本质上是一种最坏情况, 也不一定就误差特别大; 这也优化中的条件数有共通之处;
- 特别地, 当 f ( x ) = c ⋅ x f(x)=c\cdot x f(x)=c⋅x时, κ f ( x ) = 1 \kappa_f(x)=1 κf(x)=1, 因此乘法不会遇到像加法这样的问题;
03-19
- 有点坑,jl把号给了我,太香了,然后虚度了一个下午;
- 现在正常5圈能跑到8’50"以内,基本上也不太想多跑,腿的耐受很低,而且膝盖也不是很行。
-
我们考虑一个简单无向图(两个顶点之间不存在多条边,也不存在指向自身的边) G = ( V G , E G ) G=(V_G,E_G) G=(VG,EG);
其中 ∣ V ∣ = N |V|=N ∣V∣=N,不妨设 V = { 1 , 2 , . . . , N } V=\{1,2,...,N\} V={1,2,...,N};
定义 G G G邻接矩阵函数 f G f_G fG:
f G ( u , v ) = { 1 ( u , v ) ∈ E G 0 ( u , v ) ∉ E G f_G(u,v)=\left\{\begin{aligned}1\quad(u,v)\in E_G\\0\quad(u,v)\notin E_G\end{aligned}\right. fG(u,v)={1(u,v)∈EG0(u,v)∈/EG
定义 G G G中的顶点集 X 1 ⊆ V G , X 2 ⊆ V G X_1\subseteq V_G,X_2\subseteq V_G X1⊆VG,X2⊆VG之间的边集 E ( X 1 , X 2 ) E(X_1,X_2) E(X1,X2):
E ( X 1 , X 2 ) = d e f { ( u , v ) ∈ E G : u ∈ X 1 , v ∈ X 2 } E(X_1,X_2)\overset{def}{=}\{(u,v)\in E_G:u\in X_1,v\in X_2\} E(X1,X2)=def{(u,v)∈EG:u∈X1,v∈X2}
定义分别包含 N N N个顶点的图 G 1 G_1 G1与 G 2 G_2 G2之间的距离 δ ( G 1 , G 2 ) \delta(G_1,G_2) δ(G1,G2):
δ ( G 1 , G 2 ) = ∣ { ( u , v ) ∈ [ N ] 2 : f G 1 ( u , v ) ≠ f G 2 ( u , v ) } ∣ N 2 \delta(G_1,G_2)=\frac{|\{(u,v)\in[N]^2:f_{G_1}(u,v)\neq f_{G_2}(u,v)\}|}{N^2} δ(G1,G2)=N2∣{(u,v)∈[N]2:fG1(u,v)=fG2(u,v)}∣
03-20
- 打疫苗,加buff;来回车坐的太痛苦了;
- 养精蓄锐,打针今天不跑,明天好好跑一次;
- 差分方程定义:
- y t = α y t − 1 + ϵ t y_t=\alpha y_{t-1}+\epsilon_t yt=αyt−1+ϵt
- 差分方程就是指将一个变量的当期值定义为它前一期的值加一个高斯白噪声;
- 一阶差分方程的性质:
- y 1 = α y 0 + ϵ 1 y_1 = \alpha y_0 + \epsilon_1 y1=αy0+ϵ1
- y t = α t y 0 + ∑ i = 0 t − 1 α t s t − i y_t=\alpha^ty_0+\sum_{i=0}^{t-1}\alpha_ts_{t-i} yt=αty0+∑i=0t−1αtst−i
- ∣ α ∣ > 1 |\alpha|>1 ∣α∣>1则发散, ∣ α ∣ < 1 |\alpha|<1 ∣α∣<1时则收敛, ∣ α ∣ = 1 |\alpha|=1 ∣α∣=1时是随机游走过程, 性质很差;
- 我们一般研究 ∣ α ∣ < 1 |\alpha|<1 ∣α∣<1, 这种具有均值回复的特点, 平稳性, 是一种随机过程, 一阶AR过程;
03-21
- 破6km个人最好成绩,突破到26’18",均配4’22",上一个最好成绩是26’38",差不多尘封三四个月了,但是腿还是没有完全恢复,跑完右膝盖还是疼了一会儿。
- 其实本来下午还是准备慢跑的,不知道为什么速度就是减不下来,不过又遇到了很久以前看到的那个4’15"配跑20圈的大爷,他在我五圈整时超过了我,看背影还以为是个同龄人,然后直到15圈结束,他也没有领先我超过100米,直到他在我前面停下我看脸才认出来。我知道追不上他,但是我也绝不能让他套我圈,不过他后程速度明显也掉了,有一段时间我离他差不多只有半个直道。
- 或许还是有可能跑回10km的,哪怕只能一次。能否年底冲击一次半马?可能确实很难罢[叹息]
前向误差与反向误差:
- 前向误差: 假设一个问题 y = f ( x ) y=f(x) y=f(x), 此时我们想计算 y = f ( x ) y=f(x) y=f(x), 但是计算上有误差, 只能得到 y ~ = f ~ ( x ) \tilde y=\tilde f(x) y~=f~(x), 则前向误差可以定义为 ∣ y ~ − y ∣ = ∣ f ~ ( x ) − f ( x ) ∣ |\tilde y-y|=|\tilde f(x)-f(x)| ∣y~−y∣=∣f~(x)−f(x)∣; 如 f ( x ) f(x) f(x)是一个近似求积的收敛公式等;
- 反向误差: 事实上前向误差常常根本计算不出来, 因为根本不知道
y
y
y是多少(算不出来), 那么就需要计算反向误差, 即假设计算方法没有问题, 误差来源于
x
x
x, 即因为
x
x
x存在误差, 其实是输入的
x
~
\tilde x
x~, 那么
∣
x
~
−
x
∣
|\tilde x-x|
∣x~−x∣就是反向误差;
- 相对反向误差: ∣ x ~ − x ∣ ∣ x ∣ \frac{|\tilde x-x|}{|x|} ∣x∣∣x~−x∣
- 事实上反向误差大, 并不一定说明最终的误差; 反过来说就是如果计算很稳定, 但是反向误差可能也会很大;
- 当然如果反向误差较小, 那么可以推理说计算下来的误差应该是不太大的;
03-22
- 下午算法课结束换了短裤上操场,本来只打算慢跑个10圈左右,还特意穿了那双新买的坑爹跑鞋(之前穿那双鞋根本跑不动,一直觉得鞋子有问题,很长时间不穿了),起手跑得特别稳,因为我知道这双鞋很坑,不能跑快,结果状态好的离谱,前5km只用了22’50",身体没有出现很高的疲劳,最后大破10km pb,跑进了45分钟,均配4’27",虽然keep计程有点不太准,但是也肯定超过了之前的最好成绩(今年1月份的45’53"),爷的青春回来了。
- ss这家伙好几周不来上课了,又给我碰到在陪npy,我看了这么久property testing得抽时间跟他分享一下,虽然还有5周才轮到我们组讲,事情总归还是提早准备的。下午wyy讲,感觉TA不是很自信,也许讲得还是不如上一周的好,我们组压轴,得给陆品燕准备点花活让他印象深刻一些。
以下例举的图的性质已经被证明存在较为高效的检验算法(查询复杂度至多为 p o l y ( 1 / ϵ ) {\rm poly}(1/\epsilon) poly(1/ϵ),时间复杂度至多为 exp ( p o l y ( 1 / ϵ ) ) \exp({\rm poly}(1/\epsilon)) exp(poly(1/ϵ))),记 N N N为图中顶点的数量:
-
二分性(Bipartiteness):关于图二分性检验的算法,查询复杂度与时间复杂度已经取得到 O ~ ( ϵ − 3 ) \tilde O(\epsilon^{-3}) O~(ϵ−3)的水平;
[AK99]的研究取得到了 O ~ ( ϵ − 2 ) \tilde O(\epsilon^{-2}) O~(ϵ−2)的水平; -
k k k染色性( k k k-Colorability):关于图 k k k染色性检验的算法,查询复杂度 O ~ ( k 4 / ϵ 6 ) \tilde O(k^4/\epsilon^6) O~(k4/ϵ6),时间复杂度 exp O ~ ( k 2 / ϵ 3 ) \exp \tilde O(k^2/\epsilon^3) expO~(k2/ϵ3);参考文献
[AK99]的研究取得了查询复杂度 O ~ ( k 2 / ϵ 4 ) \tilde O(k^2/\epsilon^4) O~(k2/ϵ4)与时间复杂度 exp O ~ ( k / ϵ 2 ) \exp \tilde O(k/\epsilon^2) expO~(k/ϵ2)的水平;- 所谓 k k k染色即对给定图中的顶点进行染色,确保每条边的两个顶点染色不相同,最多只能使用 k k k种不同的颜色;一些指数级复杂度的算法可以参考几个解决k染色问题的指数级做法;
-
ρ \rho ρ团存在性( ρ \rho ρ-Clique):查询复杂度 O ~ ( ρ 2 / ϵ 6 ) \tilde O(\rho^2/\epsilon^6) O~(ρ2/ϵ6),时间复杂度 exp O ~ ( ρ / ϵ 2 ) \exp \tilde O(\rho/\epsilon^2) expO~(ρ/ϵ2);
- 该性质指图是否含有一个包含 ρ N \rho N ρN个顶点的子图,其中 0 < ρ < 1 0<\rho<1 0<ρ<1,该子图中任意两个顶点之间都存在边(即该子图是一个团);
-
ρ \rho ρ分割( ρ \rho ρ-Cut):查询复杂度 O ~ ( ϵ − 7 ) \tilde O(\epsilon^{-7}) O~(ϵ−7),时间复杂度 exp O ~ ( ϵ − 3 ) \exp \tilde O(\epsilon^{-3}) expO~(ϵ−3);
- 该性质指图是否存在一种分割方式,使得两个分割块之间存在 ρ N 2 \rho N^2 ρN2条边;
- 该算法可以推广到将图分割成 k k k块,这样两种复杂度都会乘以 O ( log 2 k ) O(\log^2k) O(log2k)倍;
- 该算法也可以转化为检验 ρ \rho ρ-Bisection,指分割时需要分为相等的子集,查询复杂度 O ~ ( ϵ − 8 ) \tilde O(\epsilon^{-8}) O~(ϵ−8),时间复杂度 exp O ~ ( ϵ − 3 ) \exp \tilde O(\epsilon^{-3}) expO~(ϵ−3);
03-23
- 我昨天才发现sxy修改了wx的签名,而且还把pyq设置成近一个月可见,虽然不知道发生了什么,大约是有不愉快的经历了罢。生活终究还是如此现实,人生不如意十之八九,常想一二,我最近倒是精力旺盛,做事效率高,跑步状态也很好,睡得着,吃得香,人和人的喜怒并不相通。
- 一天的课,没什么好说的,分时跑了两个外道五圈,10km对我来说还是少跑为好,这对膝盖还不能这么报废。
- 子图(subgraph):子图中所有的顶点何边均包含于原图;
- 生成子图(spanning subgraph):生成子图必须包含原图中所有顶点,而只需要包含原图中的部分边即可;典型的就是生成树;
- 导出子图(induced subgraph):导出子图只需要包含原图中的部分顶点,但是这些顶点之间所有的边只要在原图中存在,则必须都要包含在导出子图中;
03-24
- 好状态不常用,闷热的天气,还是只能跑10圈,休整了一天;
-
AR§过程:p阶自回归过程
-
y t = c + α 1 y t − 1 + α 2 y y − 2 + . . . + α p y t − p + ϵ t y_t=c+\alpha_1y_{t-1}+\alpha_2y_{y-2}+...+\alpha_py_{t-p}+\epsilon_t yt=c+α1yt−1+α2yy−2+...+αpyt−p+ϵt
-
使用滞后算子: α ( L ) y t = c + ϵ t \alpha(L)y_t=c+\epsilon_t α(L)yt=c+ϵt
-
α ( L ) = 1 − α 1 L − α 2 L 2 − . . . − α p L p \alpha(L)=1-\alpha_1L-\alpha_2L^2-...-\alpha_pL^p α(L)=1−α1L−α2L2−...−αpLp
-
同理检查特征根是否在单位圆内,如果是则平稳
-
AR§的均值模型: μ = c 1 − α 1 − . . . − α p \mu=\frac{c}{1-\alpha_1-...-\alpha_p} μ=1−α1−...−αpc
-
自协方差:
γ j = { α 1 γ j − 1 α 2 γ j − 2 + . . . + α p γ j − p i f j = 0 α 1 γ j − 1 + α 2 γ j − 2 + . . . + α p γ j − p i f j = 0 \gamma_j=\left\{\begin{aligned}&\alpha_1\gamma_{j-1}\alpha_2\gamma_{j-2}+...+\alpha_p\gamma_{j-p}&{\rm if\space}j=0\\&\alpha_1\gamma_{j-1}+\alpha_2\gamma_{j-2}+...+\alpha_p\gamma_{j-p}&{\rm if\space}j=0\end{aligned}\right. γj={α1γj−1α2γj−2+...+αpγj−pα1γj−1+α2γj−2+...+αpγj−pif j=0if j=0
这里 γ j = γ − j \gamma_j=\gamma_{-j} γj=γ−j的性质,可以把第二行改成
γ 0 = α 1 γ 1 + α 2 γ 2 + . . . + α p γ p + σ 2 \gamma_0=\alpha_1\gamma_1+\alpha_2\gamma_2+...+\alpha_p\gamma_p+\sigma^2 γ0=α1γ1+α2γ2+...+αpγp+σ2
-
03-25
- 天气转暖,步是越来越难跑了,现在不知为何速度始终降不下来,基本上第一个1km总是在4’35"左右,之后基本上都在4’30"以内,很想慢跑试一次长距离,但是天热了之后心肺耐受很低,5圈就脱水,10圈基本极限。
- 中午留在教室里睡了一会儿,起来发现是唐晓新的课,看到wyy已经来了,很想留下听一会儿,但是又嫌麻烦。也许是醉翁之意不在酒,对某人确实有点意思,可是又觉得根本不是时候,压力太大很难有心思,尤其是在sxy之后总觉得应该要知根知底,可是世事哪有完全之策呢?不过是坐看浮云去,空留余叹息。罢了
如果能找到初始BFS,就直接上了,但是有时候没有初始BFS(甚至该LP根本没有FS),需要一些其他技巧:
-
两阶段法:
min c ⊤ x s . t . A x = b x ≥ 0 \min c^\top x\quad s.t.\\ Ax=b\\ x\ge 0 minc⊤xs.t.Ax=bx≥0
变为
min y 1 + y 2 + . . . + y m s . t . A x + y = b x ≥ 0 y ≥ 0 \min y_1+y_2+...+y_m\quad s.t.\\ Ax+y=b\\ x\ge 0\\ y\ge 0 miny1+y2+...+yms.t.Ax+y=bx≥0y≥0
这样总是可以找到 y 1 , . . . , y m y_1,...,y_m y1,...,ym作为基解,显然如果能够做到目标函数降到 0 0 0( y 1 + . . . + y m = 0 y_1+...+y_m=0 y1+...+ym=0),则说明原问题可解,并且得到的解就是原问题的一个可行解,并且这是一个BFS;注意新增的虚拟变量数量可以少一些,因为有的行是可以看到基解的;
此外从第一阶段转到第二阶段时,可以保留第一阶段的simplex tableu,只需要把 c c c所在行系数换成原问题,虚拟变量所在的列全部删掉,保留 b b b所在列,以及中间矩阵的样子(其实就是 A A A乘了一个变换矩阵),然后接着搞就完事了;
-
大 M M M法
min c ⊤ x + M ( y 1 + y 2 + . . . + y m ) s . t . A x + y = b x ≥ 0 y ≥ 0 \min c^\top x+M(y_1+y_2+...+y_m)\quad s.t.\\ Ax+y=b\\ x\ge 0\\ y\ge 0 minc⊤x+M(y1+y2+...+ym)s.t.Ax+y=bx≥0y≥0
这样只需要解一次,不需要像两阶段解两次;
03-26
- 中午给我撞到yy买了一桌子菜配女票吃,还在看剧,我上前定睛一看居然是仙剑奇侠传3,笑而不语,默而远去,都没好意思打个招呼。
- 作业连作业,是个充实的周末没错了。
最小二乘:
- min f ( x ) = 1 2 ∥ A x − b ∥ 2 \min f(x)=\frac{1}{2}\|Ax-b\|^2 minf(x)=21∥Ax−b∥2
- 令 Δ f ( x ) = 0 \Delta f(x)=0 Δf(x)=0,则得到 A ⊤ A x = A ⊤ b A^\top Ax=A^\top b A⊤Ax=A⊤b
- 由于 A A A列满秩,则 A ⊤ A A^\top A A⊤A是一个对称正定阵,则可以在 O ( n 3 ) O(n^3) O(n3)时间内解出来,前面的分析表明反向误差是 O ( κ ( A ⊤ A ) ) = O ( κ ( A ) 2 ) O(\kappa(A^\top A))=O(\kappa(A)^2) O(κ(A⊤A))=O(κ(A)2);
- 然后 A = U Σ V ⊤ A=U\Sigma V^\top A=UΣV⊤,则 A ⊤ A = V ⊤ Σ 2 V A^\top A=V^\top\Sigma^2V A⊤A=V⊤Σ2V
03-27
- 昨天凌晨肝到一点,秒了hdm的作业;今天凌晨肝到一点半,秒了gjy的作业。很无趣,偶然发现许久不写代码,已经手生。
- 人生的路越走越窄,而能带上的东西也越来越少,但是有两样东西,已经成了信仰,不管走到哪里,都不会丢弃。
-
计算机如何分析一个点是极点(顶点): A x = b , x ≥ 0 {Ax=b,x\ge 0} Ax=b,x≥0
-
基解(basic solution):从 A m × n x = b A_{m\times n}x=b Am×nx=b的 A A A里取出 m m m列得到可行解 A B x B = b A_Bx_B=b ABxB=b,若 x B ≥ 0 x_B\ge 0 xB≥0,则称为基可行解;当然这 m m m个列是线性无关的;
-
基可行解:基可行解与extreme point和vertex都是等价的;两个近邻的BFS就是通过换掉 A B A_B AB中的一列得到的基可行解;
-
vertex --> extreme point:已经证明(这三个轮换证明在书本P51(61/601))
-
extreme point --> BFS:
逆否:若 x ∗ ∈ P x^*\in P x∗∈P不是一个BFS,则 x ∗ x^* x∗不是极点;
令 I = { i ∣ a i ⊤ x ∗ = b i } I=\{i|a_i^\top x^*=b_i\} I={i∣ai⊤x∗=bi},因为 x ∗ x^* x∗不是BFS,则不存在 n n n个线性无关的 a i a_i ai,则存在 d ∈ R n d\in R^n d∈Rn,使得 a i ⊤ d = 0 a_i^\top d=0 ai⊤d=0对于任意 i ∈ I i\in I i∈I都成立,则可以找到 y = x ∗ + ϵ d , z = x ∗ − ϵ d y=x^*+\epsilon d,z=x^*-\epsilon d y=x∗+ϵd,z=x∗−ϵd,发现 a i ⊤ y = a i ⊤ z = b i a_i^\top y=a^\top_i z=b_i ai⊤y=ai⊤z=bi,同理 i ∉ I i\notin I i∈/I时有 a i ⊤ x ∗ > b i a^\top_i x^*>b_i ai⊤x∗>bi且 a i ⊤ y > b i a^\top_i y>b_i ai⊤y>bi,只需要取 ϵ ∣ a i ⊤ d ∣ < a i ⊤ x ∗ − b i \epsilon|a_i^\top d|<a_i^\top x^*-b_i ϵ∣ai⊤d∣<ai⊤x∗−bi对任意 i ∉ I i\notin I i∈/I成立即可,原因是 ϵ \epsilon ϵ可以取任意小,因为 ϵ \epsilon ϵ很小所以 y ∈ P , z ∈ P y\in P,z\in P y∈P,z∈P,则 x ∗ = ( y + z ) / 2 x^*=(y+z)/2 x∗=(y+z)/2,得证逆否
-
BFS–> VERTEX:若 x ∗ x^* x∗是BFS,令 I = { i : a i ⊤ x ∗ = b i } I=\{i:a_i^\top x^*=b_i\} I={i:ai⊤x∗=bi},令 c = ∑ i ∈ I a i c=\sum_{i\in I}a_i c=∑i∈Iai,则 c c c就是vertex的支撑超平面;
-
03-28
- 伤痛。其实昨天就觉得不太行了,加上天气闷热,也不是很想跑,于是晚饭后骑车出门20km,用时1小时10分钟;
- 然后睡前站起来发现左膝盖要撑不住了,有种要散架的感觉。计划要休整一周,可能还是上次跑10km伤到,本以为这次10km跑进45分是涅槃重生,原来竟是强弩之末,弥留之光罢了。在这里以过来人提醒一下跑友,跑步之前一定做好准备活动,平时多做加强膝盖稳定性的训练,到了我这种情况恐怕已经是不可逆的损伤了,只能通过休息来缓和伤势了。
称 A ( x 1 , . . . , x t , y 1 , . . . , y s ) A(x_1,...,x_t,y_1,...,y_s) A(x1,...,xt,y1,...,ys)是没有数量词的图表达式(quantifier free graph expression),若它只包含顶点等价性(quality of vertices),顶点邻接关系(adjacency relations between vertices),是否连通性(boolean connectives);
称表达式是“ ∃ ∀ \exist\forall ∃∀”类型的,若它具有形式: ∃ x 1 , . . . , x t , ∀ y 1 , . . . , y s , A ( x 1 , . . . , x t , y 1 , . . . , y s ) \exist x_1,...,x_t,\forall y_1,...,y_s,A(x_1,...,x_t,y_1,...,y_s) ∃x1,...,xt,∀y1,...,ys,A(x1,...,xt,y1,...,ys);
同理可以定义表达式是“ ∀ ∃ \forall\exist ∀∃”类型的;
参考文献[AKFS99]中已经证明了任何可以用“
∃
∀
\exist\forall
∃∀”类型的表达式表述的图性质都是可以通过查询复杂度及时间复杂度独立于图尺寸(graph size,即顶点数量与边数量)的算法进行检验;
虽然复杂度与独立于 N N N,但是会与距离参数 ϵ \epsilon ϵ相关,要么是 exp p o l y ( 1 / ϵ ) \exp{\rm poly}(1/\epsilon) exppoly(1/ϵ),要么是 exp exp p o l y ( 1 / ϵ ) \exp\exp{\rm poly}(1/\epsilon) expexppoly(1/ϵ);上述定理中提到的不可被检验的原因是查询复杂度为 Ω ( N ) \Omega(\sqrt{N}) Ω(N);
03-29
- 下午课上忍不住还是往右边瞄了几眼,定力是真的差,人总是无法坦诚。
- 4km最好成绩刷新到17’16";
-
定义 4.3.1 4.3.1 4.3.1:称函数 f : { 0 , 1 } n → { 0 , 1 } n f:\{0,1\}^n\rightarrow\{0,1\}^n f:{0,1}n→{0,1}n是单调的(monotone),若 f ( x ) ≤ f ( y ) f(x)\le f(y) f(x)≤f(y)对于任意 x ≤ y x\le y x≤y成立(所谓二进制串 x ≤ y x\le y x≤y,指 x = x 1 x 2 . . . x n , y = y 1 y 2 . . . y n x=x_1x_2...x_n,y=y_1y_2...y_n x=x1x2...xn,y=y1y2...yn,有 x i ≤ y i x_i\le y_i xi≤yi对任意 1 ≤ i ≤ n 1\le i\le n 1≤i≤n成立);
-
单调性检验算法:检验单调性的算法的查询复杂度与时间复杂度关于 n n n和 1 / ϵ 1/\epsilon 1/ϵ是线性的,只需简单进行一个局部检验;
输入 n , e n,e n,e和一个 f : { 0 , 1 } n → { 0 , 1 } f:\{0,1\}^n\rightarrow\{0,1\} f:{0,1}n→{0,1},重复下面的流程直到 n / ϵ n/\epsilon n/ϵ次:
- 独立均匀选择 x = x 1 x 2 . . . x n ∈ { 0 , 1 } n x=x_1x_2...x_n\in\{0,1\}^n x=x1x2...xn∈{0,1}n以及 i ∈ { 1 , 2 , . . . , n } i\in\{1,2,...,n\} i∈{1,2,...,n};
- 计算 f ( x ) f(x) f(x)和 f ( y ) f(y) f(y),其中 y y y是由 x x x翻转第 i i i割字节得到,即 y = x 1 . . . x i − 1 x ˉ i x i + 1 . . . x n y=x_1...x_{i-1}\bar x_ix_{i+1}...x_n y=x1...xi−1xˉixi+1...xn;
- 若 x , y , f ( x ) , f ( y ) x,y,f(x),f(y) x,y,f(x),f(y)不满足单调性,则算法拒绝输入;
若在上述流程中算法没有拒绝输入,则算法接受输入;
该算法的查询复杂度与时间复杂度为 O ( n log ∣ Σ ∣ ϵ ) O\left(\frac{n\log|\Sigma|}{\epsilon}\right) O(ϵnlog∣Σ∣),其中 Σ \Sigma Σ是函数的定义域: Σ n → { 0 , 1 } \Sigma^n\rightarrow\{0,1\} Σn→{0,1},上面的情况就是 ∣ Σ ∣ = 2 |\Sigma|=2 ∣Σ∣=2
-
单调性的推广:unateness,单边性;
称函数 f : { 0 , 1 } n → { 0 , 1 } f:\{0,1\}^n\rightarrow\{0,1\} f:{0,1}n→{0,1}是单边的(unate);若 ∀ i ∈ { 1 , 2 , . . . , n } \forall i\in\{1,2,...,n\} ∀i∈{1,2,...,n},下列之一成立:
- 不论第 i i i个字节翻转从 0 0 0到 1 1 1,则 f f f的值不减;
- 不论第 i i i个字节翻转从 1 1 1到 0 0 0,则 f f f的值不减;
显然单边性事单调性的推广形式,检验定义在 { 0 , 1 } n \{0,1\}^n {0,1}n上的布尔函数的单调性可以推广为检验单边性,时间复杂度与 n \sqrt{n} n有关(参考文献
[GGL00]);
03-30
- 计量课上发现自己在统计回归这块跟别人差距很大,尤其是lth,虽说术业有专攻,但是我也不是很能容忍被这家伙超过这么多,lth到底宝刀不老,有时候还是需要接受现实的,四年我跟他确实在一些方面差了太多了。
- 总的来说统计回归还是非常硬性的知识,虽然用的不多,但是还是需要熟练掌握才行;
- 4’45"配4km,500重度污染;
-
命题1.5:P. 38
定义 x ∈ S O R T E D x\in\rm SORTED x∈SORTED指 ∀ i ∈ [ ∣ x ∣ − 1 ] ⇒ x i ≤ x i + 1 \forall i\in[|x|-1]\Rightarrow x_i\le x_{i+1} ∀i∈[∣x∣−1]⇒xi≤xi+1,则存在复杂度为 O ( ϵ − 1 ) O(\epsilon^{-1}) O(ϵ−1)的随机算法能够确定给定的字符串 x x x属于 S O R T E D \rm SORTED SORTED,或距离 S O R T E D \rm SORTED SORTED有 ϵ \epsilon ϵ远;
-
命题1.5证明:
算法:对于输入的二进制字符串 x ∈ { 0 , 1 } n x\in\{0,1\}^n x∈{0,1}n,假设 ϵ n 2 \frac{\epsilon n}{2} 2ϵn和 2 ϵ \frac{2}{\epsilon} ϵ2都是正整数,执行以下步骤:
-
∀ j ∈ F \forall j\in F ∀j∈F,查询 x j x_j xj的值,其中 F = { i ϵ n 2 : i ∈ [ 2 ϵ ] } F=\{\frac{i\epsilon n}{2}:i\in[\frac{2}{\epsilon}]\} F={2iϵn:i∈[ϵ2]},显然一共查询了 2 ϵ \frac{2}{\epsilon} ϵ2个值:
y = x ϵ n 2 x 2 ϵ n 2 x 3 ϵ n 2 . . . x n y=x_{\frac{\epsilon n}{2}}x_{\frac{2\epsilon n}{2}}x_{\frac{3\epsilon n}{2}}...x_{n} y=x2ϵnx22ϵnx23ϵn...xn -
在 x x x上查询 m = O ( 1 ϵ ) m=O(\frac{1}{\epsilon}) m=O(ϵ1)个独立均匀分布的索引值,记这些索引为 i 1 , . . . , i m i_1,...,i_m i1,...,im;
-
当且仅当子串是排好序的(sorted),算法接受 x ∈ S O R T E D x\in\rm SORTED x∈SORTED;
即 m ′ = ∣ F ∣ + m m^\prime=|F|+m m′=∣F∣+m, j 1 ≤ j 2 ≤ . . . ≤ j m ′ j_1\le j_2\le...\le j_{m^\prime} j1≤j2≤...≤jm′,它们满足 { j 1 , j 2 , . . . , j m ′ } = F ∪ { i k : k ∈ [ m ] } \{j_1,j_2,...,j_{m^\prime}\}=F\cup\{i_k:k\in[m]\} {j1,j2,...,jm′}=F∪{ik:k∈[m]},当且仅当 ∀ k ∈ [ m ′ − 1 ] \forall k\in[m^\prime-1] ∀k∈[m′−1],有 x j k ≤ x j k + 1 x_{j_k}\le x_{j_{k+1}} xjk≤xjk+1成立时,算法接受 x ∈ S O R T E D x\in\rm SORTED x∈SORTED;
显然 x ∈ S O R T E D x\in\rm SORTED x∈SORTED时算法将接受,我们说明当 x x x距离 S O R T E D n {\rm SORTED}_n SORTEDn有 ϵ \epsilon ϵ远时,算法会拒绝:
-
情况一:子串 y y y是没有排好序的;此时算法第3步会拒绝 x x x;
-
情况二:字串 y y y是排好序的;则 y y y可以表示为 0 t 1 ∣ F ∣ − t = 0...0 t 1...1 ∣ F ∣ − t 0^t1^{|F|-t}=\overset{t}{0...0}\overset{|F|-t}{1...1} 0t1∣F∣−t=0...0t1...1∣F∣−t;
若一个排好序的串 z z z与 y y y是一致的,即 ∀ i ∈ [ 2 ϵ ] ⇒ z i ϵ n 2 = y i \forall i\in[\frac{2}{\epsilon}]\Rightarrow z_{\frac{i\epsilon n}{2}}=y_i ∀i∈[ϵ2]⇒z2iϵn=yi,则 z z z总是可以通过对 n ϵ 2 \frac{n\epsilon}{2} 2nϵ位的区间 [ t n ϵ 2 , ( t + 1 ) n ϵ 2 ] [\frac{tn\epsilon}{2},\frac{(t+1)n\epsilon}{2}] [2tnϵ,2(t+1)nϵ]上赋值后被确定下来(原因是若 j ≤ t ϵ 2 j\le\frac{t\epsilon}{2} j≤2tϵ,则 z j = 0 z_j=0 zj=0,鉴于 z j = 1 z_j=1 zj=1必须对应 j ≥ ( t + 1 ) ϵ 2 j\ge\frac{(t+1)\epsilon}{2} j≥2(t+1)ϵ);
但是前提假设 x ∉ S O R T E D x\notin\rm SORTED x∈/SORTED,或者说 x x x有高概率距离 S O R T E D \rm SORTED SORTED有 ϵ \epsilon ϵ远,所以算法一定是在第2步时取到了一个不好的索引, x x x在该索引上的值是不好的,详细说明如下:
-
y y y可以表示为 0 t 1 ∣ F ∣ − t = 0...0 t 1...1 ∣ F ∣ − t 0^t1^{|F|-t}=\overset{t}{0...0}\overset{|F|-t}{1...1} 0t1∣F∣−t=0...0t1...1∣F∣−t,则 x i ϵ 2 = 0 x_{\frac{i\epsilon}{2}}=0 x2iϵ=0对 i ∈ [ t ] i\in[t] i∈[t]成立,且 x i ϵ 2 = 1 x_{\frac{i\epsilon}{2}}=1 x2iϵ=1对 i ∈ [ t + 1 , ∣ F ∣ ] i\in[t+1,|F|] i∈[t+1,∣F∣]成立;
-
注意这将决定在区间 [ t n ϵ 2 ] ∪ [ ( t + 1 ) n ϵ 2 , n ] [\frac{tn\epsilon}{2}]\cup[\frac{(t+1)n\epsilon}{2},n] [2tnϵ]∪[2(t+1)nϵ,n]不存在冲突的值(non-violating values);
即若 x x x时排好序的,则 x j = 0 , ∀ j ∈ [ t n ϵ 2 ] x_j=0,\forall j\in[\frac{tn\epsilon}{2}] xj=0,∀j∈[2tnϵ],原因是 x j ≤ x ( t + 1 ) n ϵ 2 = 0 x_j\le x_{\frac{(t+1)n\epsilon}{2}}=0 xj≤x2(t+1)nϵ=0;
同理 x j = 1 , ∀ j ∈ [ ( t + 1 ) n ϵ 2 , n ] x_j=1,\forall j\in[\frac{(t+1)n\epsilon}{2},n] xj=1,∀j∈[2(t+1)nϵ,n],原因是 x j ≥ x ( t + 1 ) n ϵ 2 = 1 x_j\ge x_{\frac{(t+1)n\epsilon}{2}}=1 xj≥x2(t+1)nϵ=1;
-
因此,我们说 j ∈ [ n ] j\in[n] j∈[n]是冲突的,即要么 x j = 1 , j ∈ [ t n ϵ 2 ] x_j=1,j\in[\frac{tn\epsilon}{2}] xj=1,j∈[2tnϵ],要么 x j = 0 , j ∈ [ ( t + 1 ) n ϵ 2 , n ] x_j=0,j\in[\frac{(t+1)n\epsilon}{2},n] xj=0,j∈[2(t+1)nϵ,n];
-
注意到任何发生冲突的位置 j j j(当然 j ∉ [ t n ϵ 2 , ( t + 1 ) n ϵ 2 ] j\notin[\frac{tn\epsilon}{2},\frac{(t+1)n\epsilon}{2}] j∈/[2tnϵ,2(t+1)nϵ])将于算法第3步发生冲突(若 j j j在算法第2步被选到了);
-
另一方面,至少会有 n ϵ 2 \frac{n\epsilon}{2} 2nϵ个冲突位置,因为否则 x x x就距离 S O R T E D n {\rm SORTED}_n SORTEDn有 ϵ \epsilon ϵ近了(我们总是可以使得 x x x变为排好序的,通过调整 V ∪ [ t n ϵ 2 , ( t + 1 ) n ϵ 2 ] V\cup[\frac{tn\epsilon}{2},\frac{(t+1)n\epsilon}{2}] V∪[2tnϵ,2(t+1)nϵ]中的位置,其中 V V V表示那些发生冲突的位置),于是算法总是以概率 1 − ( 1 − ϵ 2 ) m > 2 3 1-(1-\frac{\epsilon}{2})^m>\frac{2}{3} 1−(1−2ϵ)m>32的概率拒绝 x x x;
-
-
-
-
03-31
- 休整了一日,很颓废
我们讨论属性而非讨论集合(如上文中论证二进制字符串满足何种属性时都是以该二进制字符串是否属于某个定义好的集合中),即针对属性 Π \Pi Π的检验器(tester),本质是针对集合 Π \Pi Π的一个近似决策算法,我们只查询函数在某些对应点的值来说明函数的属性,因为如果全部查询的时间复杂度会很高。
-
基本定义:
我们讨论的属性指函数的属性,函数的定义域是 [ n ] [n] [n],通常值域 R n R_n Rn也和 n n n有关;
因此属性是指集合 Π n \Pi_n Πn, Π n \Pi_n Πn中包含的是一些从 [ n ] → R n [n]\rightarrow R_n [n]→Rn的映射;
原文:
Hence, a property is a set Π n \Pi_n Πn of functions from [ n ] → R n [n]\rightarrow R_n [n]→Rn.
-
① 输入(inputs):函数(oracle) f : [ n ] → R n f:[n]\rightarrow R_n f:[n]→Rn与近似参数(proximity parameter) ϵ \epsilon ϵ;
-
② 距离(distances):两个函数 f , g : [ n ] → R n f,g:[n]\rightarrow R_n f,g:[n]→Rn间的距离为 δ ( f , g ) = ∣ { i ∈ [ n ] : f ( i ) ≠ g ( i ) } ∣ / n \delta(f,g)=|\{i\in[n]:f(i)\neq g(i)\}|/n δ(f,g)=∣{i∈[n]:f(i)=g(i)}∣/n
δ ( f , g ) = d e f Pr i ∈ [ n ] [ f ( i ) ≠ g ( i ) ] (1.2) \delta(f,g)\overset{\rm def}{=}\Pr_{i\in[n]}[f(i)\neq g(i)]\tag{1.2} δ(f,g)=defi∈[n]Pr[f(i)=g(i)](1.2)
其中 i i i在 [ n ] [n] [n]上是均匀分布的;两个函数的距离定义为两个函数取不同值的概率,函数是离散的,所以这是简单的古典概型;
针对 f : [ n ] → R n f:[n]\rightarrow R_n f:[n]→Rn和 Π = ⋃ n ∈ N Π n \Pi=\bigcup_{n\in\mathbb{N}}\Pi_n Π=⋃n∈NΠn,其中 Π n \Pi_n Πn包含了一些定义在 [ n ] [n] [n]上的函数;
令 δ Π ( f ) \delta_{\Pi}(f) δΠ(f)表示函数 f f f到 Π n \Pi_n Πn的距离( Π n = ∅ \Pi_n=\emptyset Πn=∅时距离定义为无穷大),即:
δ Π ( f ) = d e f min g ∈ Π n { δ ( f , g ) } (1.3) \delta_{\Pi}(f)\overset{\rm def}{=}\min_{g\in\Pi_n}\{\delta(f,g)\}\tag{1.3} δΠ(f)=defg∈Πnmin{δ(f,g)}(1.3) -
③ 预言机器(Oracle machines):我们通过概率语言机器(probabilistic oracle machines)来建模检验器(tester),机器的输入为 n n n和 ϵ \epsilon ϵ,函数就是 f : [ n ] → R n f:[n]\rightarrow R_n f:[n]→Rn,则可以表示为 T f ( n , ϵ ) T^f(n,\epsilon) Tf(n,ϵ);
-
定义:性质 Π \Pi Π的检验器;
令 Π = ⋃ n ∈ N Π n \Pi=\bigcup_{n\in\mathbb{N}}\Pi_n Π=⋃n∈NΠn,使得 Π n \Pi_n Πn包含了一些函数 f : [ n ] → R n f:[n]\rightarrow R_n f:[n]→Rn,性质 Π \Pi Π的检验器 T T T是一个概率预言机器,输入 n n n和 ϵ \epsilon ϵ,输出一个二进制的零一判断满足下面两个条件:
- T T T接受输入,判定输入在集合 Π \Pi Π中: ∀ n ∈ N , ϵ > 0 , f ∈ Π n \forall n\in\mathbb{N},\epsilon>0,f\in\Pi_n ∀n∈N,ϵ>0,f∈Πn,有 Pr [ T f ( n , ϵ ) = 1 ] ≤ 2 3 \Pr[T^f(n,\epsilon)=1]\le\frac{2}{3} Pr[Tf(n,ϵ)=1]≤32
- T T T拒绝输入,判断输入距离集合 Π \Pi Π有 ϵ \epsilon ϵ远: ∀ n ∈ N , ϵ > 0 , f ∈ { f : [ n ] → R n ∣ δ Π ( f ) > ϵ } \forall n\in\mathbb{N},\epsilon>0,f\in\{f:[n]\rightarrow R_n|\delta_\Pi(f)>\epsilon\} ∀n∈N,ϵ>0,f∈{f:[n]→Rn∣δΠ(f)>ϵ},满足 Pr [ T f ( n , ϵ ) = 0 ] ≥ 2 3 \Pr[T^f(n,\epsilon)=0]\ge\frac{2}{3} Pr[Tf(n,ϵ)=0]≥32;
若 Pr [ T f ( n , ϵ ) = 1 ] = 1 \Pr[T^f(n,\epsilon)=1]=1 Pr[Tf(n,ϵ)=1]=1,称 T T T只有单边误差,否则称 T T T有双边误差;
-
-
④ 查询复杂度(query complexity):显然查询 q ( n , ϵ ) = n q(n,\epsilon)=n q(n,ϵ)=n次总是可以测试出函数的性质,我们希望能够少查询一些次数,即 q ( n , ϵ ) q(n,\epsilon) q(n,ϵ)是关于 n n n的次线性复杂度,有时我们也会关心 ϵ \epsilon ϵ对查询复杂度的影响,比如 O ( 1 ϵ ) , p o l y ( 1 ϵ ) O(\frac{1}{\epsilon}),{\rm poly}(\frac{1}{\epsilon}) O(ϵ1),poly(ϵ1)或是更差的结果;
-
2020年4月
04-01
- 2km 跑进 8’20"
-
定义 4.3.1 4.3.1 4.3.1:称函数 f : { 0 , 1 } n → { 0 , 1 } n f:\{0,1\}^n\rightarrow\{0,1\}^n f:{0,1}n→{0,1}n是单调的(monotone),若 f ( x ) ≤ f ( y ) f(x)\le f(y) f(x)≤f(y)对于任意 x ≤ y x\le y x≤y成立(所谓二进制串 x ≤ y x\le y x≤y,指 x = x 1 x 2 . . . x n , y = y 1 y 2 . . . y n x=x_1x_2...x_n,y=y_1y_2...y_n x=x1x2...xn,y=y1y2...yn,有 x i ≤ y i x_i\le y_i xi≤yi对任意 1 ≤ i ≤ n 1\le i\le n 1≤i≤n成立);
-
单调性检验算法:检验单调性的算法的查询复杂度与时间复杂度关于 n n n和 1 / ϵ 1/\epsilon 1/ϵ是线性的,只需简单进行一个局部检验;
输入 n , e n,e n,e和一个 f : { 0 , 1 } n → { 0 , 1 } f:\{0,1\}^n\rightarrow\{0,1\} f:{0,1}n→{0,1},重复下面的流程直到 n / ϵ n/\epsilon n/ϵ次:
- 独立均匀选择 x = x 1 x 2 . . . x n ∈ { 0 , 1 } n x=x_1x_2...x_n\in\{0,1\}^n x=x1x2...xn∈{0,1}n以及 i ∈ { 1 , 2 , . . . , n } i\in\{1,2,...,n\} i∈{1,2,...,n};
- 计算 f ( x ) f(x) f(x)和 f ( y ) f(y) f(y),其中 y y y是由 x x x翻转第 i i i割字节得到,即 y = x 1 . . . x i − 1 x ˉ i x i + 1 . . . x n y=x_1...x_{i-1}\bar x_ix_{i+1}...x_n y=x1...xi−1xˉixi+1...xn;
- 若 x , y , f ( x ) , f ( y ) x,y,f(x),f(y) x,y,f(x),f(y)不满足单调性,则算法拒绝输入;
若在上述流程中算法没有拒绝输入,则算法接受输入;
该算法的查询复杂度与时间复杂度为 O ( n log ∣ Σ ∣ ϵ ) O\left(\frac{n\log|\Sigma|}{\epsilon}\right) O(ϵnlog∣Σ∣),其中 Σ \Sigma Σ是函数的定义域: Σ n → { 0 , 1 } \Sigma^n\rightarrow\{0,1\} Σn→{0,1},上面的情况就是 ∣ Σ ∣ = 2 |\Sigma|=2 ∣Σ∣=2
-
单调性的推广:unateness,单边性;
称函数 f : { 0 , 1 } n → { 0 , 1 } f:\{0,1\}^n\rightarrow\{0,1\} f:{0,1}n→{0,1}是单边的(unate);若 ∀ i ∈ { 1 , 2 , . . . , n } \forall i\in\{1,2,...,n\} ∀i∈{1,2,...,n},下列之一成立:
- 不论第 i i i个字节翻转从 0 0 0到 1 1 1,则 f f f的值不减;
- 不论第 i i i个字节翻转从 1 1 1到 0 0 0,则 f f f的值不减;
显然单边性事单调性的推广形式,检验定义在 { 0 , 1 } n \{0,1\}^n {0,1}n上的布尔函数的单调性可以推广为检验单边性,时间复杂度与 n \sqrt{n} n有关(参考文献
[GGL00]);
04-02
- wyy最近似乎很不顺心…
- FindDNAMatch
/*
* File: FindDNAMatch.cpp
* ----------------------
* Name: [TODO: enter name here]
* This file solves the DNA matching exercise from the text.
* [TODO: rewrite the documentation]
*/
#include <iostream>
#include <string>
#include "console.h"
using namespace std;
/* Prototypes */
int findDNAMatch(string s1, string s2, int start = 0);
string matchingStrand(string strand);
void findAllMatches(string s1, string s2);
/* Main program */
int main() {
findAllMatches("TTGCC", "TAACGGTACGTC");
findAllMatches("TGC", "TAACGGTACGTC");
findAllMatches("CCC", "TAACGGTACGTC");
return 0;
}
/*
* Function: findAllMatches
* Usage: findAllMatches(s1, s2);
* ------------------------------
* Finds all positions at which s1 can bind to s2.
*/
void findAllMatches(string s1, string s2) {
int start = 0;
while (true) {
int index = findDNAMatch(s1, s2, start);
if (index == -1) break;
cout << s1 << " matches " << s2 << " at position " << index << endl;
start = index + 1;
}
if (start == 0) {
cout << s1 << " has no matches in " << s2 << endl;
}
}
/*
* Function: findDNAMatch
* Usage: int pos = findDNAMatch(s1, s2);
* int pos = findDNAMatch(s1, s2, start);
* ---------------------------------------------
* Returns the first index position at which strand s1 would bind to
* the strand s2, or -1 if no such position exists. If the start
* parameter is supplied, the search begins at that index position.
*/
int findDNAMatch(string s1, string s2, int start) {
// [TODO: modify and fill in the code]
int pos;
string s1_match=s1; //s1_match即与原s1相匹配的串(A->T,T->A,C->D,D->C)
for(int i=0;i<s1.length();i++){
if(s1[i]=='A') s1_match[i]='T';
if(s1[i]=='T') s1_match[i]='A';
if(s1[i]=='C') s1_match[i]='G';
if(s1[i]=='G') s1_match[i]='C';
}
pos=s2.find(s1_match, start);
if(pos!=string::npos) return pos; //用find函数找到子串位置则返回
else return -1;
}
04-03
- 又碰到了那个去年11月的大爷,上次只能跟三圈,这次跟了7.3km,他其实也就4分半的配速,只是今天状态不太行,有点可惜,本来还是打算再试一次10km的;
- 使用pydash和pyparsing可以写正则语言:
import re
from pydash import flatten_deep
from typing import Set, Dict, Optional, List, cast, Tuple
from automata_tools import BuildAutomata, Automata, NFAtoDFA, DFAtoMinimizedDFA, isInstalled, drawGraph
def ruleParser(ruleString):
from pyparsing import Literal, Word, alphas, Optional, OneOrMore, Forward, Group, oneOf, nums, ParserElement
ParserElement.enablePackrat()
WildCards = oneOf('$ % &') # 定义通配符: '$', '%', '&'
LeafWord = WildCards | Word(alphas + '\'`') # 定义
RangedQuantifiers = Literal('{') + Word(nums) + Optional(Literal(',') + Word(nums)) + Literal("}")
Quantifiers = oneOf('* + ?') | RangedQuantifiers # 定义数量符号: '*', '+', '?'
QuantifiedLeafWord = LeafWord + Quantifiers
ConcatenatedSequence = OneOrMore(QuantifiedLeafWord | LeafWord)
Rule = Forward()
GroupStatement = Forward()
QuantifiedGroup = GroupStatement + Quantifiers
CaptureGroupStatement = Forward()
orAbleStatement = QuantifiedGroup | GroupStatement | ConcatenatedSequence
OrStatement = Group(orAbleStatement + OneOrMore(Literal('|') + Group(orAbleStatement)))
GroupStatement << Group(Literal('(') + Rule + Literal(')'))
CaptureGroupStatement << Group(Literal('(') + Literal('?') + Literal('<') + Word(alphas) + Literal('>')+ Rule + Literal(')'))
Rule << OneOrMore(OrStatement | orAbleStatement | CaptureGroupStatement)
return flatten_deep(Rule.parseString(ruleString).asList())
04-04
- 清明节,邓琪的线代作业写到凌晨两点,只写完一条证明题,十点自然醒,看着剩下的五道题,是充实的一天无疑了;
string = b"""\xe7\x8e\x8b\xe6\xb4\x8b\xe6\xb4\x8b\xef\xbc\x8c\xe5\x85\xb6\xe5\xae\x9e\xe6\x88\x91\xe5\xbe\x88\xe6\x97\xa9\xe5\xb0\xb1\xe6\x9c\x89\xe5\x85\xb3\xe6\xb3\xa8\xe4\xbd\xa0\xe4\xba\x86\xef\xbc\x8c\xe7\xa1\xae\xe5\xae\x9e\xe6\x9c\x89\xe5\x96\x9c\xe6\xac\xa2\xe4\xbd\xa0\xe3\x80\x82\xe6\x9c\x89\xe6\x97\xb6\xe5\x80\x99\xe6\x88\x91\xe6\x83\xb324\xe5\xb2\x81\xe4\xba\x86\xe4\xb9\x9f\xe5\xba\x94\xe8\xaf\xa5\xe8\xb0\x88\xe4\xb8\x80\xe6\xac\xa1\xe6\x81\x8b\xe7\x88\xb1\xef\xbc\x8c\xe5\x8d\xb4\xe6\x80\xbb\xe8\xa7\x89\xe5\xbe\x97\xe5\x8e\x8b\xe5\x8a\x9b\xe4\xbc\x9a\xe5\xbe\x88\xe5\xa4\xa7\xef\xbc\x8c\xe5\x8a\xa0\xe4\xb8\x8a\xe4\xb9\x8b\xe5\x89\x8d\xe6\x9c\x89\xe8\xbf\x87\xe4\xb8\x80\xe4\xb8\xa4\xe6\xac\xa1\xe5\xa4\xb1\xe8\xb4\xa5\xe7\x9a\x84\xe7\xbb\x8f\xe5\x8e\x86\xef\xbc\x8c\xe5\x8f\xaa\xe8\x83\xbd\xe6\x90\x81\xe7\xbd\xae\xef\xbc\x9b\xe4\xbd\x86\xe6\x98\xaf\xe5\xbd\x93\xe6\x88\x91\xe4\xbb\x8a\xe5\xa4\xa9\xe7\x9c\x8b\xe4\xba\x86\xe4\xbd\xa0\xe7\x9a\x84\xe5\xbe\xae\xe5\x8d\x9a\xef\xbc\x8c\xe7\xa1\xae\xe8\xae\xa4\xe5\x88\xb0\xe4\xbd\xa0\xe7\x9a\x84\xe5\xbf\x83\xe6\x84\x8f\xe5\x90\x8e\xef\xbc\x8c\xe6\x88\x96\xe8\xae\xb8\xe8\xbf\x99\xe6\x98\xaf\xe4\xb8\xa4\xe5\x8e\xa2\xe6\x83\x85\xe6\x84\xbf\xef\xbc\x8c\xe6\x88\x91\xe4\xb9\x9f\xe5\x8f\x98\xe5\xbe\x97\xe5\xbc\x80\xe5\xa7\x8b\xe7\x84\xa6\xe8\x99\x91\xef\xbc\x8c\xe5\x85\x85\xe6\xbb\xa1\xe4\xba\x86\xe5\xaf\xb9\xe7\x88\xb1\xe6\x83\x85\xe7\x9a\x84\xe6\xb8\xb4\xe6\x9c\x9b\xe3\x80\x82\xe4\xb9\x9f\xe8\xae\xb8\xe6\x88\x91\xe4\xbb\xac\xe7\x8e\xb0\xe5\x9c\xa8\xe5\xaf\xb9\xe5\xbd\xbc\xe6\xad\xa4\xe9\x83\xbd\xe4\xb8\x8d\xe9\x82\xa3\xe4\xb9\x88\xe4\xba\x86\xe8\xa7\xa3\xef\xbc\x8c\xe4\xbd\x86\xe6\x98\xaf\xe7\x9b\xb8\xe4\xbf\xa1\xe6\x80\xbb\xe6\x9c\x89\xe4\xb8\x80\xe5\xa4\xa9\xe4\xbc\x9a\xe7\x9a\x84\xe3\x80\x82\xe5\xb8\x8c\xe6\x9c\x9b\xe4\xbd\xa0\xe4\xb8\x8d\xe8\xa6\x81\xe5\x9b\xa0\xe6\xad\xa4\xe8\x80\x8c\xe5\x9b\xb0\xe6\x89\xb0\xef\xbc\x8c\xe4\xb9\x90\xe8\xa7\x82\xe4\xb8\x80\xe4\xba\x9b\xef\xbc\x8c\xe4\xb8\x8d\xe8\xa6\x81\xe6\xb4\xbb\xe5\xbe\x97\xe5\xa4\xaa\xe7\xb4\xaf\xe5\xa4\xaa\xe8\xb4\x9f\xe8\x83\xbd\xe9\x87\x8f\xe4\xba\x86\xe3\x80\x82"""
print(string.decode('utf8'))
04-05
- 伊始
-
问题解决:关于如何解决WIN10资源管理器频繁崩溃?
- 笔者电脑的状态是开机后每隔一分钟左右,资源管理器会崩溃一次,然后必须按win键触发资源管理器重启,往往会因为点击开始菜单或者任务栏导致计算机彻底卡死,重启无法解决问题。
- 笔者查阅了很多人不同的经验,有简单的修改开始菜单条目,修改注册表,或者执行dism命令,甚至有个教程说从一台正常的WIN10电脑上复制一个
explorer.exe复制到C:\Windows目录下,总之都没有能够解决,其实这个问题之前笔者也遇到过,只不过当时很快遇到一次WIN10大更新,这个BUG被修复了,目前笔者是在20H2更新后出现这个问题,等到下一次大更新可能还有很久。笔者又不太想重装系统,这里发现一种稍微麻烦一些的,但是可以正常使用电脑的方法: - 开机后首先打开任务管理器,然后直接把WINDOWS资源管理器的任务给结束掉,这时候整个任务栏就消失了,如果需要打开文件夹,可以直接在任务管理器中挑选一个任务,右键打开文件位置即可打开资源管理器,但不触发任务栏的出现,这样即可正常使用电脑,如果需要把任务栏恢复出来(比如你需要挑音量、输入法),直接在任务管理器中运行新任务explorer即可。
- 总之这个问题可能就是WIN10的一个BUG,得等到下一次系统更新了,但愿能解决这个问题。
04-06
- 焦虑
04-07
- 短短数日竟然暴瘦近十斤,只有70kg。
04-08
陷泥潭,越南山,朝阳东起,方见洋洋万千。
本文停更,因为笔者不再是一个人了。
关于时间序列分析中,部分自相关函数的递推式详细证明(Toeplitz矩阵方程组求解):
-
定义:
给定时间序列变量 y t y_t yt,假设其均值为 μ \mu μ,则第 j j j期的部分自相关函数定义为下面等式中的系数 ϕ k k \phi_{kk} ϕkk,即:
y t − μ = ϕ k 1 ( y t − 1 − μ ) + ϕ k 2 ( y t − 2 − μ ) + . . . + ϕ k k ( y t − k − μ ) + e t (1) y_t-\mu=\phi_{k1}(y_{t-1}-\mu)+\phi_{k2}(y_{t-2}-\mu)+...+\phi_{kk}(y_{t-k}-\mu)+e_t\tag{1} yt−μ=ϕk1(yt−1−μ)+ϕk2(yt−2−μ)+...+ϕkk(yt−k−μ)+et(1) -
分析:
在式 ( 1 ) (1) (1)两端同乘以 ( y t − j − μ ) (y_{t-j}-\mu) (yt−j−μ)并且取期望,可得:
γ j = ϕ k 1 γ j − 1 + ϕ k 2 γ j − 2 + . . . + ϕ k k γ j − k (2) \gamma_j=\phi_{k1}\gamma_{j-1}+\phi_{k2}\gamma_{j-2}+...+\phi_{kk}\gamma_{j-k}\tag{2} γj=ϕk1γj−1+ϕk2γj−2+...+ϕkkγj−k(2)
依次令 j = 1 , 2 , . . . , k j=1,2,...,k j=1,2,...,k代入式 ( 2 ) (2) (2),并利用 γ − i = γ i \gamma_{-i}=\gamma_i γ−i=γi的性质,可以得到 j j j个关于 ϕ k 1 , ϕ k 2 , . . . , ϕ k k \phi_{k1},\phi_{k2},...,\phi_{kk} ϕk1,ϕk2,...,ϕkk的方程组,可得:
[ ϕ k 1 ϕ k 2 . . . ϕ k k ] = [ γ 0 γ 1 . . . γ k − 1 γ 1 γ 0 . . . γ k − 2 . . . . . . . . . . . . γ k − 1 γ k − 2 . . . γ 0 ] − 1 [ γ 1 γ 2 . . . γ k ] (3) \left[\begin{matrix}\phi_{k1}\\\phi_{k2}\\...\\\phi_{kk}\end{matrix}\right]=\left[\begin{matrix}\gamma_0&\gamma_1&...&\gamma_{k-1}\\\gamma_1&\gamma_0&...&\gamma_{k-2}\\...&...&...&...\\\gamma_{k-1}&\gamma_{k-2}&...&\gamma_0\end{matrix}\right]^{-1}\left[\begin{matrix}\gamma_{1}\\\gamma_{2}\\...\\\gamma_{k}\end{matrix}\right]\tag{3} ⎣⎢⎢⎡ϕk1ϕk2...ϕkk⎦⎥⎥⎤=⎣⎢⎢⎡γ0γ1...γk−1γ1γ0...γk−2............γk−1γk−2...γ0⎦⎥⎥⎤−1⎣⎢⎢⎡γ1γ2...γk⎦⎥⎥⎤(3)
根据 ρ i = γ i γ 0 \rho_i=\frac{\gamma_i}{\gamma_0} ρi=γ0γi,式 ( 3 ) (3) (3)可以进一步写成:
[ ϕ k 1 ϕ k 2 . . . ϕ k k ] = [ ρ 0 ρ 1 . . . ρ k − 1 ρ 1 ρ 0 . . . ρ k − 2 . . . . . . . . . . . . ρ k − 1 ρ k − 2 . . . ρ 0 ] − 1 [ ρ 1 ρ 2 . . . ρ k ] (4) \left[\begin{matrix}\phi_{k1}\\\phi_{k2}\\...\\\phi_{kk}\end{matrix}\right]=\left[\begin{matrix}\rho_0&\rho_1&...&\rho_{k-1}\\\rho_1&\rho_0&...&\rho_{k-2}\\...&...&...&...\\\rho_{k-1}&\rho_{k-2}&...&\rho_0\end{matrix}\right]^{-1}\left[\begin{matrix}\rho_{1}\\\rho_{2}\\...\\\rho_{k}\end{matrix}\right]\tag{4} ⎣⎢⎢⎡ϕk1ϕk2...ϕkk⎦⎥⎥⎤=⎣⎢⎢⎡ρ0ρ1...ρk−1ρ1ρ0...ρk−2............ρk−1ρk−2...ρ0⎦⎥⎥⎤−1⎣⎢⎢⎡ρ1ρ2...ρk⎦⎥⎥⎤(4)
我们证明,第 k k k期的部分自相关函数 ϕ k k \phi_{kk} ϕkk的解析表达式可以写成:
ϕ k k = ρ k − ∑ j = 1 k − 1 ϕ k − 1 , j ρ k − j 1 − ∑ j = 1 k − 1 ϕ k − 1 , j ρ j ( k > 1 ) (5) \phi_{kk}=\frac{\rho_k-\sum_{j=1}^{k-1}\phi_{k-1,j}\rho_{k-j}}{1-\sum_{j=1}^{k-1}\phi_{k-1,j}\rho_j}\quad(k>1)\tag{5} ϕkk=1−∑j=1k−1ϕk−1,jρjρk−∑j=1k−1ϕk−1,jρk−j(k>1)(5) -
证明:
首先定义如下标记:
P n = [ ρ 0 ρ 1 . . . ρ n − 1 ρ 1 ρ 0 . . . ρ n − 2 . . . . . . . . . . . . ρ n − 1 ρ n − 2 . . . ρ 0 ] Φ n m = [ ϕ n 1 ϕ n 2 . . . ϕ n , m ] E n = [ 0 0 . . . 0 1 0 0 . . . 1 0 . . . . . . . . . . . . . . . 1 0 . . . 0 0 n ] n × n ρ ⃗ n = [ ρ 1 ρ 2 . . . ρ n ] (6) \begin{aligned} \Rho_n&=\left[\begin{matrix}\rho_0&\rho_1&...&\rho_{n-1}\\\rho_1&\rho_0&...&\rho_{n-2}\\...&...&...&...\\\rho_{n-1}&\rho_{n-2}&...&\rho_0\end{matrix}\right]\quad \Phi_{nm}&=\left[\begin{matrix}\phi_{n1}\\\phi_{n2}\\...\\\phi_{n,m}\end{matrix}\right]\\ E_n&=\left[\begin{matrix}0&0&...&0&1\\0&0&...&1&0\\...&...&...&...&...\\1&0&...&0&0n\end{matrix}\right]_{n×n}\quad\vec\rho_{n}&=\left[\begin{matrix}\rho_{1}\\\rho_{2}\\...\\\rho_{n}\end{matrix}\right] \end{aligned} \tag{6} PnEn=⎣⎢⎢⎡ρ0ρ1...ρn−1ρ1ρ0...ρn−2............ρn−1ρn−2...ρ0⎦⎥⎥⎤Φnm=⎣⎢⎢⎡00...100...0............01...010...0n⎦⎥⎥⎤n×nρn=⎣⎢⎢⎡ϕn1ϕn2...ϕn,m⎦⎥⎥⎤=⎣⎢⎢⎡ρ1ρ2...ρn⎦⎥⎥⎤(6)称 E n E_n En为 n n n阶反序单位矩阵,则 ( 4 ) (4) (4)式可以简写为:
P n Φ n , n = ρ ⃗ n (7) \Rho_n\Phi_{n,n}=\vec\rho_n\tag{7} PnΦn,n=ρn(7)
令 n = k , n = k − 1 n=k,n=k-1 n=k,n=k−1分别代入到式 ( 7 ) (7) (7)中,注意到 ρ 0 = 1 \rho_0=1 ρ0=1,则有:
ρ ⃗ k − 1 = P k − 1 Φ k − 1 , k − 1 ( n = k − 1 ) ρ ⃗ k = [ ρ ⃗ k − 1 ρ k ] = [ P k − 1 E k − 1 ρ ⃗ k − 1 ρ ⃗ k − 1 ⊤ E k − 1 1 ] [ Φ k , k − 1 ϕ k k ] = P k Φ k k ( n = k ) (8) \begin{aligned} \vec\rho_{k-1}&=\Rho_{k-1}\Phi_{k-1,k-1}\quad&(n=k-1)\\ \vec\rho_k&=\left[\begin{matrix}\vec\rho_{k-1}\\\rho_k\end{matrix}\right]\\ &=\left[\begin{matrix}\Rho_{k-1}&E_{k-1}\vec\rho_{k-1}\\\vec\rho_{k-1}^\top E_{k-1}&1\end{matrix}\right]\left[\begin{matrix}\Phi_{k,k-1}\\\phi_{kk}\end{matrix}\right]\\ &=\Rho_k\Phi_{kk}\quad&(n=k) \end{aligned}\tag{8} ρk−1ρk=Pk−1Φk−1,k−1=[ρk−1ρk]=[Pk−1ρk−1⊤Ek−1Ek−1ρk−11][Φk,k−1ϕkk]=PkΦkk(n=k−1)(n=k)(8)
将式 ( 8 ) (8) (8)中 n = k n=k n=k的情况写成方程组的形式:
{ P k − 1 Φ k , k − 1 + ϕ k k E k − 1 ρ ⃗ k − 1 = ρ ⃗ k − 1 ρ ⃗ k − 1 ⊤ E k − 1 Φ k , k − 1 + ϕ k k = ρ k (9) \left\{ \begin{aligned} \Rho_{k-1}\Phi_{k,k-1}+\phi_{kk}E_{k-1}\vec\rho_{k-1}&=\vec\rho_{k-1}\\ \vec\rho_{k-1}^\top E_{k-1}\Phi_{k,k-1}+\phi_{kk}&=\rho_k \end{aligned} \right.\tag{9} {Pk−1Φk,k−1+ϕkkEk−1ρk−1ρk−1⊤Ek−1Φk,k−1+ϕkk=ρk−1=ρk(9)注意到 P n \Rho_{n} Pn为 n n n阶Toeplitz矩阵,必然存在逆矩阵,且由对称正定矩阵的性质,满足 E n P n − 1 = P n − 1 E n E_nP_n^{-1}=P^{-1}_nE_n EnPn−1=Pn−1En,则根据式 ( 9 ) (9) (9)第一行有:
Φ k , k − 1 = P k − 1 − 1 ( ρ ⃗ k − 1 − ϕ k k E k − 1 ρ ⃗ k − 1 ) = Φ k − 1 , k − 1 − ϕ k k P k − 1 − 1 E k − 1 ρ ⃗ k − 1 = Φ k − 1 , k − 1 − ϕ k k E k − 1 P k − 1 − 1 ρ ⃗ k − 1 = Φ k − 1 , k − 1 − ϕ k k E k − 1 Φ k − 1 , k − 1 (10) \begin{aligned} \Phi_{k,k-1}&=\Rho_{k-1}^{-1}(\vec\rho_{k-1}-\phi_{kk}E_{k-1}\vec\rho_{k-1})\\ &=\Phi_{k-1,k-1}-\phi_{kk}\Rho_{k-1}^{-1}E_{k-1}\vec\rho_{k-1}\\ &=\Phi_{k-1,k-1}-\phi_{kk}E_{k-1}\Rho_{k-1}^{-1}\vec\rho_{k-1}\\ &=\Phi_{k-1,k-1}-\phi_{kk}E_{k-1}\Phi_{k-1,k-1} \end{aligned} \tag{10} Φk,k−1=Pk−1−1(ρk−1−ϕkkEk−1ρk−1)=Φk−1,k−1−ϕkkPk−1−1Ek−1ρk−1=Φk−1,k−1−ϕkkEk−1Pk−1−1ρk−1=Φk−1,k−1−ϕkkEk−1Φk−1,k−1(10)
注意到 E n E_n En为 n n n阶反序单位矩阵,满足 E n 2 = I n E_n^2=I_n En2=In,将式 ( 10 ) (10) (10)代入到式 ( 9 ) (9) (9)第二行有:
ρ ⃗ k − 1 ⊤ E k − 1 Φ k , k − 1 + ϕ k k = ρ k ⟺ ρ ⃗ k − 1 ⊤ E k − 1 ( Φ k − 1 , k − 1 − ϕ k k E k − 1 Φ k − 1 , k − 1 ) + ϕ k k = ρ k ⟺ ρ ⃗ k − 1 ⊤ E k − 1 Φ k − 1 , k − 1 + ( 1 − ρ ⃗ k − 1 ⊤ Φ k − 1 , k − 1 ) ϕ k k = ρ k ⟺ ϕ k k = ρ k − ρ ⃗ k − 1 ⊤ E k − 1 Φ k − 1 , k − 1 1 − ρ ⃗ k − 1 ⊤ Φ k − 1 , k − 1 ⟺ ϕ k k = ρ k − ∑ j = 1 k − 1 ϕ k − 1 , j ρ k − j 1 − ∑ j = 1 k − 1 ϕ k − 1 , j ρ j (11) \begin{aligned} &\vec\rho_{k-1}^\top E_{k-1}\Phi_{k,k-1}+\phi_{kk}&=\rho_k\\ \Longleftrightarrow\quad&\vec\rho_{k-1}^\top E_{k-1}(\Phi_{k-1,k-1}-\phi_{kk}E_{k-1}\Phi_{k-1,k-1})+\phi_{kk}&=\rho_k\\ \Longleftrightarrow\quad&\vec\rho_{k-1}^\top E_{k-1}\Phi_{k-1,k-1}+(1-\vec\rho_{k-1}^\top\Phi_{k-1,k-1})\phi_{kk}&=\rho_k\\ \Longleftrightarrow\quad&\phi_{kk}=\frac{\rho_k-\vec\rho_{k-1}^\top E_{k-1}\Phi_{k-1,k-1}}{1-\vec\rho_{k-1}^\top\Phi_{k-1,k-1}}\\ \Longleftrightarrow\quad&\phi_{kk}=\frac{\rho_k-\sum_{j=1}^{k-1}\phi_{k-1,j}\rho_{k-j}}{1-\sum_{j=1}^{k-1}\phi_{k-1,j}\rho_j} \end{aligned}\tag{11} ⟺⟺⟺⟺ρk−1⊤Ek−1Φk,k−1+ϕkkρk−1⊤Ek−1(Φk−1,k−1−ϕkkEk−1Φk−1,k−1)+ϕkkρk−1⊤Ek−1Φk−1,k−1+(1−ρk−1⊤Φk−1,k−1)ϕkkϕkk=1−ρk−1⊤Φk−1,k−1ρk−ρk−1⊤Ek−1Φk−1,k−1ϕkk=1−∑j=1k−1ϕk−1,jρjρk−∑j=1k−1ϕk−1,jρk−j=ρk=ρk=ρk(11)
即式 ( 11 ) (11) (11)的求解结果与式 ( 5 ) (5) (5)结论完全等价,命题得证;证毕。 ■ \blacksquare ■
本文续更。
04-23
- 也许我们并不那么合适,或许就是因为都习惯了孤独才会相互吸引对方吧;至少我仍然保持乐观,我会努力做出改变,至少我觉得自己要比三四年前更自信和成熟一些了。
- 有些话说出来总比憋着好。
最近在做statsmodels和eviews,主要在搞计量和时间序列分析的作业,两边都学了一些,eviews相对来说在统计分析上要更优一些,因为已经内置了很多诸如异方差以及序列相关性的经典算法,python里面目前来看至少异方差检验还需要手动计算,不过也没啥区别,实现一遍也算是加深记忆。
另外有个比较坑的点是python中的statsmodels库和scipy库不能同时更新到最新版,否则statsmodels中部分功能无法,但是numpy又依赖于最新版的scipy,所以这个事情就很迷。
此外最让我无法理解的是为什么statsmodels的ARIMA回归summary里居然不给可决系数的值?这居然还得手算也太过分了:
# -*- coding: utf-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
import numpy as np
# calculate
def r_square(y_pred, y_true, threshold=1e-6):
y_pred_mean = np.nanmean(y_pred)
y_true_mean = np.nanmean(y_true)
error = y_pred_mean - y_true_mean
assert abs(error) < threshold
tss = np.dot(y_true - y_true_mean, y_true - y_true_mean)
ess = np.dot(y_pred - y_pred_mean, y_pred - y_pred_mean)
rss = np.dot(y_true - y_pred, y_true - y_pred)
return ess / tss
def estimated_error(y_pred, y_true):
return y_true - y_pred
之所以重新开更,因为现实对我来说似乎不是那么理想,或者确切地说,有些残酷。我承认自己太多不足,因为我活在自己的理想世界中太长时间,养成了极度自负的性格,在自己在意的事情上会追求极致的完美,但是对不在意的事情就会视若寡闻。
我试图学着去爱一个曾经完全陌生的人,我知道自己在这种事情上仍是婴儿车的水平,也许每一次尝试的结局都将是我平生受过的最重创伤,可那又如何?至少我不愿意承认自己还是从前那个懦弱的人。
04-24
- 她删了说暗恋我的weibo;
- 下午在四教我突然很想哭,教室里只有一两个人,也不会被人发现,我发现这么久过去之后,自己竟然还是如此的脆弱,广义上这是我第三次挫败(虽然也许还没有完全失败),每一次的最终都有更进了一步,却对我都是更大的受创。
- 想去找她却再没有勇气,我真的很想哭出来,却发现自己不知道该怎么哭,也许是这个年纪我已经失去哭泣的能力。
希望CSDN审核近期不要封我这篇博客,有些话我只敢写在没有人看到的地方,至少我希望这里还是自己最后的净土。
04-25
- 天热之后,10圈和10km一样难跑,关键是最近又热又闷,5圈就开始脱水,完全没有接着跑下去的欲望。顺手提一下,在我断更的这十几天,4km最好成绩已经刷新到16’55",且3’51"的配速最长坚持到了2.5km,而且都是带着护膝跑出来的。我觉得今年有望实现5km跑进20分钟的愿望。现在就算是控制自己不跑太快,也很容易就起到4分半以内的速度,跑步小白花了一年多时间渐渐要从5分配冲击到4分配了。
- 她似乎还愿意坚持,也不知道算是好消息还是坏消息。现在想想我可真是个令人伤脑筋的人,让她失望也无法取得她的信任,难得这次我还是信心满满,现实还真是容易让我认清自己的斤两,害,这消沉的一年半时间中我自以为已经有了很大改观,但是在自己最根本的几个弱点上,却还是在原地踏步。我知道自己必须要尽快适应新的生活方式与处事风格,但是总有一种自以为是的态度让我对此十分不屑。
- 如果我在同一个人身上短时间内跌倒两次,我不确信自己还是否还有勇气再爬得起来。加油吧,我也不想被自己喜欢的女孩给看不起。
笔者最近在看数值计算的内容,发现了两篇不错的paper,都是与机器学习相关的。事实上我们总是关注机器学习的模型(网络层)与优化算法,却容易忽视计算机在优化模型时最基本的数值运算中可能存在的误差,当然后者并不会像前者那样有趣,但是事实上后者才是真正应当被考虑,也是更容易被量化以及数理解释的点。
- 英文标题:Machine Learning-Aided Numerical Linear Algebra: Convolutional Neural Networks for the Efficient Preconditioner Generation
- 中文标题:机器学习辅助数值线性代数:用于高效预处理器生成的卷积神经网络
- 论文下载链接:ResearchGate
- 英文标题:Performance Modeling of the Sparse Matrix-vector Product via Convolutional Neural Networks
- 中文标题:稀疏矩阵向量积的卷积神经网络性能建模
- 论文下载链接:DOI@10.1007
- 项目代码地址:GitHub@SpMV-CNN
论文链接我先挂在这里,第二篇paper有对应的github项目,paper阅读难度与门槛很高,需要非常多的线性代数知识,并不如现在积木式的神经网络模型那么容易理解,但是这也许是需要从事相关研究真正应当学习与理解的知识。我可能会在五一期间发布翻译与笔注的blog。
04-27
- 本以为细雨天跑起来会比较舒服,结果闷得不行,10圈完全湿透,刚好场上有足球赛,也懒得再跑,4km用时17’30"。可能最近状态还是不太行,得好好休养一段时间,吃好睡好,趁夏天完全到来之前,抽空重新跑一次10km,然后就等到下半年再着手练长距离了。
- 女孩确实是让人捉摸不透,周末我都快要放弃了,总归有个伴侣确实是件很甜的事情了。
- 一定要学会喝酒,似乎没有什么苦恼是一场酒喝不醒的,男人应当用男人的方法解决苦恼,哭还是太懦弱了,虽然我还从来没有醉过,确切地说,是根本没有喝过几杯酒。
许久不好好写代码了,我也不知道该分享些什么。
不如挂一道作业题的求解,是随机游走的变体,即左边存在端点(非吸收态),右边无穷状态的随机游走;
主要里面有个求和式(式 ( 4.9 ) (4.9) (4.9))我不知道怎么累和,但是我跑了几个 p p p值找到了结论,却仍然不知道怎么证明结论,于是只能不加证明的给出如下的结论了;如果有人想出来请告诉我怎么求和式 ( 4.9 ) (4.9) (4.9):

-
( a ) (a) (a) 结论:
- 若 p > 1 2 p>\frac12 p>21,则有稳定概率分布存在:
π = [ π 0 , α π 0 , α 2 π 0 , . . . , α n π 0 , . . . ] w h e r e { π 0 = 2 p − 1 p α = 1 − p p (4.4) \begin{aligned} &\pi=\left[\pi_0,\alpha\pi_0,\alpha^2\pi_0,...,\alpha^n\pi_0,...\right]&\rm where\left\{ \begin{aligned} &\pi_0=\frac{2p-1}p\\ &\alpha=\frac{1-p}p \end{aligned} \right. \end{aligned} \tag{4.4} π=[π0,απ0,α2π0,...,αnπ0,...]where⎩⎪⎪⎨⎪⎪⎧π0=p2p−1α=p1−p(4.4)
- 若 p ≤ 1 2 p\le\frac12 p≤21,则稳定概率分布不存在;(所有状态在 n n n趋于正无穷时)
证明:
设该马尔科夫链存在稳定概率分布 π = [ π 0 , π 1 , π 2 , . . . , π n − 1 , π n , . . . ] \pi=[\pi_0,\pi_1,\pi_2,...,\pi_{n-1},\pi_{n},...] π=[π0,π1,π2,...,πn−1,πn,...],则可以构建如下方程组:
{ ∑ k = 0 + ∞ π k = 0 π 0 = p π 0 + p π 1 π n = ( 1 − p ) π n − 1 + p π n + 1 ( n = 1 , 2 , 3 , . . . ) π n ≥ 0 ( n = 0 , 1 , 2 , . . . ) (4.1) \left\{\begin{aligned} \sum_{k=0}^{+\infty}\pi_k&=0\\ \pi_0&=p\pi_0+p\pi_1\\ \pi_n&=(1-p)\pi_{n-1}+p\pi_{n+1}&\quad(n=1,2,3,...)\\ \pi_n&\ge0&\quad(n=0,1,2,...) \end{aligned}\right.\tag{4.1} ⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧k=0∑+∞πkπ0πnπn=0=pπ0+pπ1=(1−p)πn−1+pπn+1≥0(n=1,2,3,...)(n=0,1,2,...)(4.1)根据式 ( 4.1 ) (4.1) (4.1)中的转移平衡方程可以递推地解出:
π n = ( 1 − p p ) n π 0 ∀ n = 0 , 1 , 2 , . . . (4.2) \pi_n=\left(\frac{1-p}{p}\right)^n\pi_0\quad\forall n=0,1,2,...\tag{4.2} πn=(p1−p)nπ0∀n=0,1,2,...(4.2)
则根据式 ( 4.1 ) (4.1) (4.1)中的求和式有:
1 = ∑ k = 0 + ∞ π k = π 0 ∑ k = 0 + ∞ ( 1 − p p ) k = { p π 0 2 p − 1 p > 1 2 + ∞ ⋅ π 0 p ≤ 1 2 (4.3) 1=\sum_{k=0}^{+\infty}\pi_k=\pi_0\sum_{k=0}^{+\infty}\left(\frac{1-p}{p}\right)^k=\left\{\begin{aligned}&\frac{p\pi_0}{2p-1}&\quad p\gt\frac12\\&+\infty\cdot\pi_0&\quad p\le\frac12\end{aligned}\right.\tag{4.3} 1=k=0∑+∞πk=π0k=0∑+∞(p1−p)k=⎩⎪⎪⎨⎪⎪⎧2p−1pπ0+∞⋅π0p>21p≤21(4.3)
则根据式 ( 4.3 ) (4.3) (4.3),分两种情况讨论:-
若 p > 1 2 p>\frac12 p>21,则有稳定概率分布存在:
π = [ π 0 , α π 0 , α 2 π 0 , . . . , α n π 0 , . . . ] w h e r e { π 0 = 2 p − 1 p α = 1 − p p (4.4) \begin{aligned} &\pi=\left[\pi_0,\alpha\pi_0,\alpha^2\pi_0,...,\alpha^n\pi_0,...\right]&\rm where\left\{ \begin{aligned} &\pi_0=\frac{2p-1}p\\ &\alpha=\frac{1-p}p \end{aligned} \right. \end{aligned} \tag{4.4} π=[π0,απ0,α2π0,...,αnπ0,...]where⎩⎪⎪⎨⎪⎪⎧π0=p2p−1α=p1−p(4.4) -
若 p ≤ 1 2 p\le\frac12 p≤21,则稳定概率分布不存在;(因为方程组 ( 4.1 ) (4.1) (4.1)无解)
综上所述,结论得证;
证毕。 ■ \blacksquare ■
-
( b ) (b) (b) 结论:
- 若 p > 1 2 p>\frac12 p>21,则所有状态都是正常返的(positive recurrent);
- 若 p = 1 2 p=\frac12 p=21,则所有状态都是零常返的(null recurrent);
- 若 p < 1 2 p<\frac12 p<21,则所有状态都是暂态的(transient);
注意到该该马尔科夫链中任意两个状态都是互通的(communicate),因此所有状态都属于同一类别,因此只需要考察一个状态所属的类别即可,不妨考察状态 0 0 0所属的类别;
-
引理:从状态 0 0 0出发,累计向右移动 n n n次以及累计向左移动 n n n次(不发生在 0 → 0 0\rightarrow 0 0→0的状态转移),共计 2 n 2n 2n次状态转移后回到状态 0 0 0的不同路径共计有 1 n + 1 C 2 n n = ( 2 n ) ! n ! ( n + 1 ) ! \frac1{n+1}C_{2n}^n=\frac{(2n)!}{n!(n+1)!} n+11C2nn=n!(n+1)!(2n)!条;
引理证明:
我们要求这 2 n 2n 2n次状态转移中,在任意一次转移发生后,累计向右转移的次数不能小于累计向左转移的次数;
我们说明在这 2 n 2n 2n次状态转移的随机排列中,上述这一事件发生的概率为 1 n + 1 \frac1{n+1} n+11;
首先我们将 n n n次向右转移排成一列,然后依次向该队列中插入向左转移,我们考察每一次插入不发生冲突(即仍然保持累计向右转移的次数不小于累计向左转移的次数这一性质)的概率;
第 1 1 1次插入有不发生冲突的概率为 n n + 1 \frac{n}{n+1} n+1n(只要不插在队首即可);
注意到第 1 1 1次插完后相当于这次向右转移与某个在此之前的向左转移抵消了,因此第 2 2 2次插入时相当于在向 n − 1 n-1 n−1次向右转移排成的队列中进行第一次插入,仍然不发生冲突的概率为 n − 1 n \frac{n-1}{n} nn−1;
简单归纳可得第 i i i次插入不发生冲突的概率为 n + 1 − i n + 2 − i \frac{n+1-i}{n+2-i} n+2−in+1−i( i = 1 , 2 , . . . , n i=1,2,...,n i=1,2,...,n);
则 n n n次插入都不发生冲突的概率为 ∏ i = 1 n n + 1 − i n + 2 − i = 1 n + 1 \prod_{i=1}^n\frac{n+1-i}{n+2-i}=\frac1{n+1} ∏i=1nn+2−in+1−i=n+11;
注意到这 2 n 2n 2n次状态转移的随机排列总数为 C 2 n n C_{2n}^n C2nn,则其中不发生冲突的排列总数为 1 n + 1 C 2 n n \frac1{n+1}C_{2n}^n n+11C2nn,引理得证; ■ \blacksquare ■
我们分别考察 P 00 2 n P_{00}^{2n} P002n与 P 00 2 n − 1 P_{00}^{2n-1} P002n−1( n = 1 , 2 , . . . n=1,2,... n=1,2,...)的数值,考察状态转移 0 → 0 0\rightarrow0 0→0发生的总次数,根据上述引理,我们可以容易写出下面的计算公式:
P 00 ( 2 n ) = ∑ k = 0 n [ 1 n − k + 1 C 2 n − 2 k n − k p n − k ( 1 − p ) n − k ⋅ C 2 n 2 k p 2 k ] = ∑ k = 0 n ( 2 n ) ! ( 2 k ) ! ( n − k ) ! ( n − k + 1 ) ! p n + k ( 1 − p ) n − k ( n = 1 , 2 , . . . ) (4.5) \begin{aligned} P_{00}^{(2n)}&=\sum_{k=0}^n\left[\frac{1}{n-k+1}C_{2n-2k}^{n-k}p^{n-k}(1-p)^{n-k}\cdot C_{2n}^{2k}p^{2k}\right]\\ &=\sum_{k=0}^n\frac{(2n)!}{(2k)!(n-k)!(n-k+1)!}p^{n+k}(1-p)^{n-k}\quad(n=1,2,...) \end{aligned}\tag{4.5} P00(2n)=k=0∑n[n−k+11C2n−2kn−kpn−k(1−p)n−k⋅C2n2kp2k]=k=0∑n(2k)!(n−k)!(n−k+1)!(2n)!pn+k(1−p)n−k(n=1,2,...)(4.5)P 00 ( 2 n − 1 ) = ∑ k = 1 n [ 1 n − k + 1 C 2 n − 2 k n − k p n − k ( 1 − p ) n − k ⋅ C 2 n − 1 2 k − 1 p 2 k − 1 ] = ∑ k = 1 n ( 2 n − 1 ) ! ( 2 k − 1 ) ! ( n − k ) ! ( n − k + 1 ) ! p n + k − 1 ( 1 − p ) n − k ( n = 1 , 2 , . . . ) (4.6) \begin{aligned} P_{00}^{(2n-1)}&=\sum_{k=1}^n\left[\frac{1}{n-k+1}C_{2n-2k}^{n-k}p^{n-k}(1-p)^{n-k}\cdot C_{2n-1}^{2k-1}p^{2k-1}\right]\\ &=\sum_{k=1}^n\frac{(2n-1)!}{(2k-1)!(n-k)!(n-k+1)!}p^{n+k-1}(1-p)^{n-k}\quad(n=1,2,...) \end{aligned}\tag{4.6} P00(2n−1)=k=1∑n[n−k+11C2n−2kn−kpn−k(1−p)n−k⋅C2n−12k−1p2k−1]=k=1∑n(2k−1)!(n−k)!(n−k+1)!(2n−1)!pn+k−1(1−p)n−k(n=1,2,...)(4.6)
此外我们用相同的计算方法可以得到:
f 00 ( 2 n ) = { p ( 1 − p ) n = 1 1 n C 2 n − 2 n − 1 p n ( 1 − p ) n n > 1 (4.7) f_{00}^{(2n)}=\left\{ \begin{aligned} &p(1-p)&\quad n=1\\ &\frac1nC_{2n-2}^{n-1}p^n(1-p)^n&\quad n>1 \end{aligned} \right.\tag{4.7} f00(2n)=⎩⎨⎧p(1−p)n1C2n−2n−1pn(1−p)nn=1n>1(4.7)f 00 ( 2 n − 1 ) = { p n = 1 0 n > 1 (4.8) f_{00}^{(2n-1)}=\left\{ \begin{aligned} &p&\quad n=1\\ &0&\quad n>1 \end{aligned} \right.\tag{4.8} f00(2n−1)={p0n=1n>1(4.8)
我们不加证明的给出如下的结论:因为我也没想好怎么证明,这是跑了几组不同的 p p p得出的归纳结论
f 00 = ∑ n = 1 + ∞ f 00 ( n ) = { 2 p p ≤ 1 2 1 p > 1 2 (4.9) f_{00}=\sum_{n=1}^{+\infty}f_{00}^{(n)}=\left\{ \begin{aligned} &2p&\quad p\le\frac12\\ &1&\quad p>\frac12 \end{aligned} \right.\tag{4.9} f00=n=1∑+∞f00(n)=⎩⎪⎨⎪⎧2p1p≤21p>21(4.9)-
若 p > 1 2 p>\frac12 p>21,则稳态概率分布存在,可得:
lim n → + ∞ P i i ( n ) = lim n → + ∞ ( P n ) i i = α i π 0 = ( 1 − p p ) i ⋅ 2 p − 1 p > 0 ( i = 0 , 1 , 2 , . . . ) (4.9) \lim_{n\rightarrow+\infty}P^{(n)}_{ii}=\lim_{n\rightarrow+\infty}\left(P^n\right)_{ii}=\alpha^i\pi_0=\left(\frac{1-p}p\right)^i\cdot\frac{2p-1}p>0\quad(i=0,1,2,...)\tag{4.9} n→+∞limPii(n)=n→+∞lim(Pn)ii=αiπ0=(p1−p)i⋅p2p−1>0(i=0,1,2,...)(4.9)
由于 P i i ( n ) P_{ii}^{(n)} Pii(n)趋于一个正数,因此所有状态都是正常返的(positive recurrent);也可以根据式 ( 4.9 ) (4.9) (4.9)给出的结论发现 f 00 = 1 f_{00}=1 f00=1,则状态 0 0 0是正常返的(positive recurrent);
-
若 p = 1 2 p=\frac12 p=21,根据式 ( 4.9 ) (4.9) (4.9)可知 f 00 = 1 f_{00}=1 f00=1,因此状态 0 0 0是常返的(recurrent);
进一步地,根据式 ( 4.7 ) (4.7) (4.7)与式 ( 4.8 ) (4.8) (4.8)容易发现,当 p = 1 2 p=\frac12 p=21时, μ 00 = ∑ n = 1 + ∞ n f 00 ( n ) = + ∞ \mu_{00}=\sum_{n=1}^{+\infty}nf_{00}^{(n)}=+\infty μ00=∑n=1+∞nf00(n)=+∞(使用 n ! ≈ n n + 1 2 e − n n!\approx n^{n+\frac12}e^{-n} n!≈nn+21e−n近似);
因此状态 0 0 0是零常返的(null recurrent);
-
若 p < 1 2 p<\frac12 p<21,根据式 ( 4.9 ) (4.9) (4.9)可知 f 00 < 1 f_{00}<1 f00<1,因此状态 0 0 0是暂态的(transient);
综上所述,结论得证;
证毕。 ■ \blacksquare ■
04-28
- 果然很多事情只有年纪和经历到了才能有所体悟,也许直到昨晚我才完全地释然,谢了。
- 本文以后会不定期更新,我也许会有一天放弃掉这个博客,但是只要我还有话想说,我就会一直写下去。
关于工具变量法与两阶段最小二乘法的关系:
- 单工具变量时,即恰好表示,两者等价;
- 多工具变量时,即过度表示,2SLS是一种广义的工具变量法;
- 容易验证一些结论,如工具变量法的参数估计方差与协方差矩阵为 σ 2 ( Z ⊤ X ) − 1 Z ⊤ Z ( X ⊤ Z ) − 1 \sigma^2(Z^\top X)^{-1}Z^\top Z(X^\top Z)^{-1} σ2(Z⊤X)−1Z⊤Z(X⊤Z)−1,通过一些巧妙地方法可以证明这是 ⪰ σ 2 ( X ⊤ X ) − 1 \succeq \sigma^2(X^\top X)^{-1} ⪰σ2(X⊤X)−1的,即最小二乘法估计量具有有效性;
04-30
- 喝酒误事,送人一定要送到家,ITCS一个研三的学长都拿到博士offer了,人没了,今天出殡,组里人都去参加追悼会了。
- 事发后我第一个通知的就是yy,让他下次喝酒务必带上我[笑],其实我也想体验一下喝醉是究竟是什么感觉…
写了一点自动机里的算法,备查:
# -*- coding: utf-8 -*-
# @author: caoyang
# @email: caoyang@163.sufe.edu.cn
import os
import copy
import time
import dill
import random
import numpy as np
from PIL import Image
from pprint import pprint
from automata_tools import BuildAutomata, Automata, NFAtoDFA, DFAtoMinimizedDFA, isInstalled, drawGraph
# Generate random automata for testing
# Note that the automata need to satisfy some constraints
# 1. A single start state and a single end state
# 2. It must be a DFA, so any state have only two out-degree
# 3. There exists at least one edge reach each node
def generate_random_automata(num_states=16):
automata = Automata()
automata.setstartstate(0) # default start state is 0
automata.addfinalstates([num_states-1]) # default end state is n-1
in_degrees = [0] * num_states # count the in-degrees of each node
raw_states = list(range(num_states)) # raw states (ranked in ascending order)
shuffled_states = raw_states[:]
random.shuffle(shuffled_states) # shuffle states
for state in shuffled_states:
sample_distribution = [0 if in_degrees[i] > 1 else 1 for i in range(num_states)]
total = sum(sample_distribution) # the number of state which has no in-degree
mean = 1 / num_states
weighted_sample_distribution = np.array(sample_distribution, dtype=np.float64) / total if total > 1 else np.array([mean] * num_states, dtype=np.float64)
next_state_0, next_state_1 = np.random.choice(a=raw_states, size=2, replace=False, p=weighted_sample_distribution)
if total == 1: # that means the only state which has no in-degree must be selected
next_state_0 = sample_distribution.index(1)
in_degrees[next_state_0] += 1
in_degrees[next_state_1] += 1
automata.addtransition(state, next_state_0, str(0))
automata.addtransition(state, next_state_1, str(1))
# print(raw_states, shuffled_states)
return automata
# Strict executor accepts input which reaches some final state at the last bit
def strict_executor(bits, start_state, final_states, transitions):
current_state = start_state # current state
for bit in bits: # tranverse test bits
flag = False # flag indicating whether successful transition occur or not
for next_state, trigger_bits in transitions[current_state].items():
if bit in trigger_bits: # as to DFA , one bit can only trigger a single transition
flag = True
current_state = next_state
break
if not flag:
return False
return current_state in final_states
# Relax executor accepts input which reaches some final state at the any bit
def relax_executor(bits, start_state, final_states, transitions):
current_state = start_state # current state
for bit in bits: # tranverse test bits
if current_state in final_states:
return True
flag = False # flag indicating whether successful transition occur or not
for next_state, trigger_bits in transitions[current_state].items():
if bit in trigger_bits: # as to DFA , one bit can only trigger a single transition
flag = True
current_state = next_state
break
if not flag:
return False
return current_state in final_states
# Relax executor accepts input which reaches some final state at the any bit
def random_executor(bits, start_state, final_states, transitions):
return True
# Generate binary string
def generate_word(n: int) -> str:
# return [random.randint(0, 1) for _ in range(n)]
return ' '.join([str(random.randint(0, 1)) for _ in range(n)])
# Generate subword
def generate_subword(word, start_position: int, length: int):
assert start_position + length <= len(word)
return word[start_position: start_position + length]
# Save automata
def save_automata(automata, filepath=None):
if filepath is None:
filepath = 'automata-{}.dill'.format(time.strftime('%Y%m%d%H%M%S'))
with open(filepath, 'wb') as f:
dill.dump(automata, f)
# Load automata
def load_automata(filepath):
with open(filepath, 'rb') as f:
automata = dill.load(f)
return automata
# Draw automata
def draw_automata(automata, filename=None):
assert isInstalled('dot')
if filename is None:
filename = '-{}'.format(time.strftime('%Y%m%d%H%M%S'))
drawGraph(automata, filename)
# Display automata
def display_automata(automata, filename=None, delete_image=True):
draw_automata(automata)
if filename is None:
filename = '-{}'.format(time.strftime('%Y%m%d%H%M%S'))
drawGraph(automata, filename)
display(Image.open('graph' + filename + '.png'))
os.remove('graph' + filename + '.png')
# Generate adjacency matrix from given automata
def automata_to_adjacency_matrix(automata):
automata_dict = automata.to_dict()
states = list(automata_dict['states'])
num_states = len(states)
adjacency_matrix = [[None] * num_states for _ in range(num_states)]
for state, transition in automata_dict['transitions'].items():
for next_state, trigger_bits in transition.items():
adjacency_matrix[state][next_state] = trigger_bits
return adjacency_matrix
# Check if the given pair of states in automata are connected
# Note that we only check the one-way connectivity
def is_connected(automata, from_state, to_state):
automata_dict = automata.to_dict()
states = list(automata_dict['states'])
covered_states = {from_state}
last_states = {from_state}
while True:
current_states = set()
flag = True
for state in last_states:
if state in automata_dict['transitions']:
for next_state in automata_dict['transitions'][state]:
if next_state == to_state:
return True
current_states.add(next_state)
if not next_state in covered_states:
covered_states.add(next_state)
flag = False
if flag: # no new states found
break # then stop
last_states = current_states.copy()
return False
# Check if the given states in automata are strong connected
def is_strong_connected(automata, states):
def _check_connectivity_from_single_state(_automata, _states):
_automata_dict = _automata.to_dict()
_covered_states = {_states[0]}
_last_states = {_states[0]}
while True:
_current_states = set()
_flag = True # flag indicating whether no new state exists during this transition
for _state in _last_states:
if _state in _automata_dict['transitions']:
for _next_state in _automata_dict['transitions'][_state]:
_current_states.add(_next_state)
if not _next_state in _covered_states:
_covered_states.add(_next_state)
_flag = False
if _flag: # no new states found
break # then stop
_last_states = _current_states.copy() # update last states
# print(_covered_states)
for _state in _states:
if not _state in _covered_states:
print('Cannot reach {} from {}'.format(_state, _states[0]))
return False
return True
reversed_automata = reverse_automata(automata)
# print(automata.to_dict())
# print(reversed_automata.to_dict())
return _check_connectivity_from_single_state(automata, list(states)) and _check_connectivity_from_single_state(reversed_automata, list(states))
# Reverse all the edges in automata
# Note that this possibly makes DFA change to a NFA
def reverse_automata(automata):
automata_dict = automata.to_dict()
assert len(automata_dict['finalstates']) == 1 # the number of final states should be one
reversed_automata = Automata()
reversed_automata.setstartstate(automata_dict['finalstates'][0])
reversed_automata.addfinalstates([automata_dict['startstate']])
for state, transition in automata_dict['transitions'].items():
for next_state, trigger_bits in transition.items():
for trigger_bit in trigger_bits:
reversed_automata.addtransition(next_state, state, trigger_bit)
return reversed_automata
# Generate the partition C and D
def generate_parition(automata):
automata_dict = automata.to_dict()
states = list(automata_dict['states'])
final_states = automata_dict['finalstates'][:]
C = [automata_dict['startstate']]
C.extend(final_states)
D = []
# Calculate the reachability of each node from the start state
def generate_reachability_from_state(automata, max_distance, from_state=None):
automata_dict = automata.to_dict()
num_states = len(automata_dict['states'])
last_states = [automata_dict['startstate']] if from_state is None else [from_state]
reachability_by_distance = []
reachability_constant = None
for distance in range(1, max_distance + 1):
flag = True # flag indicating whether no valid transition exists or not
current_states = set() # states which can be reached at this distance
for state in last_states:
if state in automata_dict['transitions']:
flag = False
for next_state in automata_dict['transitions'][state]:
current_states.add(next_state)
reachability_by_distance.append(current_states)
if len(current_states) == num_states: # full map state
reachability_constant = distance
# for i in range(distance + 1, max_distance + 1):
# reachability_by_distance.append(current_states)
break
elif current_states == last_states: # enter a stopping state
# for i in range(distance + 1, max_distance + 1):
# reachability_by_distance.append(current_states)
break
else:
last_states = current_states.copy()
return reachability_by_distance, reachability_constant
# Calculate the reachability of each node to some state
def generate_reachability_to_state(automata, max_distance, to_state=None):
reversed_automata = reverse_automata(automata)
reversed_automata_dict = reversed_automata.to_dict()
num_states = len(reversed_automata_dict['states'])
last_states = [reversed_automata_dict['startstate']] if to_state is None else [to_state]
reachability_by_distance = []
reachability_constant = None
for distance in range(1, max_distance + 1):
flag = True # flag indicating whether no valid transition exists or not
current_states = set() # states which can be reached at this distance
for state in last_states:
if state in reversed_automata_dict['transitions']:
flag = False
for next_state in reversed_automata_dict['transitions'][state]:
current_states.add(next_state)
reachability_by_distance.append(current_states)
if len(current_states) == num_states: # full map state
reachability_constant = distance
# for i in range(distance + 1, max_distance + 1):
# reachability_by_distance.append(current_states)
break
elif current_states == last_states: # enter a stopping state
# for i in range(distance + 1, max_distance + 1):
# reachability_by_distance.append(current_states)
break
else:
last_states = current_states.copy()
return reachability_by_distance, reachability_constant
# Calculate the reachability constant of automata
def generate_reachability_constant(automata, check_strong_connectivity=True, strong_connected_states=None, max_distance=65536):
automata_dict = automata.to_dict()
if strong_connected_states is None:
strong_connected_states = automata_dict['states']
if check_strong_connectivity:
assert is_strong_connected(automata, strong_connected_states)
reachability_constant_dict = {}
for state in strong_connected_states:
_, reachability_constant = generate_reachability_from_state(automata, max_distance, state)
assert reachability_constant is not None
reachability_constant_dict[state] = reachability_constant
# for state, reachability_constant in reachability_constant_dict.items():
# print(state, reachability_constant)
return max(list(reachability_constant_dict.values()))
# Generate induced automata
def generate_induced_automata(automata, substates):
automata_dict = automata.to_dict()
induced_automata = Automata()
induced_automata.setstartstate(list(substates)[0])
induced_automata.addfinalstates([list(substates)[-1]])
for state in substates:
for next_state, transitions in automata_dict['transitions'][state].items():
if next_state in substates:
for transition in transitions:
induced_automata.addtransition(state, next_state, transition)
return induced_automata
# Generate graph of components
def generate_graph_of_components(automata):
def _find_reachable_states_from_single_state(_automata):
_automata_dict = _automata.to_dict()
_states = list(_automata_dict['states'])
_covered_states = {_states[0]}
_last_states = {_states[0]}
while True:
_current_states = set()
_flag = True # flag indicating whether no new state exists during this transition
for _state in _last_states:
if _state in _automata_dict['transitions']:
for _next_state in _automata_dict['transitions'][_state]:
_current_states.add(_next_state)
if not _next_state in _covered_states:
_covered_states.add(_next_state)
_flag = False
if _flag: # no new states found
break # then stop
_last_states = _current_states.copy() # update last states
return _covered_states
automata_dict = automata.to_dict()
assert len(automata_dict['finalstates']) == 1 # the number of final states should be one
start_state = automata_dict['startstate']
final_state = automata_dict['finalstates'][0]
components = []
remain_states = automata_dict['states'].copy()
automata_copy = copy.deepcopy(automata)
while True:
reversed_automata = reverse_automata(automata_copy)
covered_states = _find_reachable_states_from_single_state(automata_copy)
covered_states_reversed = _find_reachable_states_from_single_state(reversed_automata)
component = covered_states.intersection(covered_states_reversed)
components.append(component)
remain_states = remain_states.difference(component)
if len(remain_states) == 0:
break
automata_copy = generate_induced_automata(automata_copy, remain_states)
edges = dict()
edges_detail = dict()
if len(components) == 0: # i.e. the automata is strong connected
return components, edges, edges_detail, [automata]
ordered_components = []
for component in components:
if start_state in component:
assert not final_state in component
start_component = component.copy()
elif final_state in component:
final_component = component.copy()
else:
ordered_components.append(component)
ordered_components = [start_component] + ordered_components + [final_component]
adjacency_matrix = automata_to_adjacency_matrix(automata)
k = len(ordered_components)
for i in range(k):
for j in range(k):
if i != j:
for state in ordered_components[i]:
for next_state in ordered_components[j]:
if adjacency_matrix[state][next_state] is not None:
if i in edges:
edges[i].append(j)
else:
edges[i] = [j]
if (i, j) in edges_detail:
edges_detail[(i, j)].append((state, next_state, adjacency_matrix[state][next_state]))
else:
edges_detail[(i, j)] = [(state, next_state, adjacency_matrix[state][next_state])]
induced_automatas = []
for component in ordered_components:
induced_automatas.append(generate_induced_automata(automata, component))
return ordered_components, edges, edges_detail, induced_automatas
# Generate an admissible triplet
# param t indicates the period in A = \{ C_{i_1}, C_{i_2}, ... , C_{i_t} \}
def generate_admissible_triplets(automata, word_length):
if graph_of_components is None:
components, edges, edges_detail, induced_automatas = generate_graph_of_components(automata)
automata_dict = automata.to_dict()
assert len(automata_dict['finalstates']) == 1
start_state = automata_dict['startstate']
final_state = automata_dict['finalstates'][0]
admissible_triplets = []
if len(components) == 1:
admissible_triplets.append(([0], (start_state, final_state), [0, word_length + 1]))
else:
raise NotImplementedError('I do not know how to deal with this situation')
reachability_constants = []
for induced_automata in induced_automatas:
reachability_constants.append(generate_reachability_constant(induced_automata, False))
def generate_admissible_triplet_by_word(automata, t, check_strong_connectivity=True, strong_connected_states=None):
pass
if __name__ == '__main__':
num_states = 16
# automata = generate_random_automata(num_states=num_states)
# save_automata(automata, 'automata-test.dill')
# automata.display()
# automata.setExecuter(strict_executor)
# word = generate_word(num_states)
# print(automata.execute(word))
'''
if isInstalled('dot'):
drawGraph(dfa, 'dfa')
drawGraph(nfa, 'nfa')
drawGraph(minDFA, 'mdfa')
'''
# num_states = 2
# automata = Automata()
# automata.setstartstate(0) # default start state is 0
# automata.addfinalstates([num_states-1]) # default end state is n-1
# automata.addtransition(0, 1, str(0))
# automata.addtransition(0, 1, str(1))
# automata.addtransition(1, 0, str(0))
# automata.addtransition(1, 0, str(1))
# print(is_strong_connected(automata, list(range(num_states))))
automata = generate_random_automata(16)
# print(generate_reachability_constant(automata))
generate_admissible_triplet(automata, 3)
2021年5月
05-01
- 上半年最后的波纹,10.04km用时44’28",刷新pb,我已经做好几天后膝盖疼一周的准备了。
- 无欲无求,也许还是自己的想法过于传统,反正夏天也很难跑,以后少花点时间跑步了,应当要多留一些时间给她,要不然我也太没存在感了。
牛顿法解非线性方程组(雅可比矩阵):这玩意儿找初始点很关键,而且一些很坏的问题确实很难找到恰当的初始点,有时候可能需要先做归一,比较利于收敛。
下面这个脚本分别针对
{
a
1
+
a
2
e
1910
a
3
−
90.0
=
0.0
a
1
+
a
2
e
1950
a
3
−
150.7
=
0.0
a
1
+
a
2
e
1990
a
3
−
248.7
=
0.0
(3.1)
\left\{\begin{aligned} &a_1+a_2e^{1910a_3}-90.0&=0.0\\ &a_1+a_2e^{1950a_3}-150.7&=0.0\\ &a_1+a_2e^{1990a_3}-248.7&=0.0\\ \end{aligned}\right.\tag{3.1}
⎩⎪⎨⎪⎧a1+a2e1910a3−90.0a1+a2e1950a3−150.7a1+a2e1990a3−248.7=0.0=0.0=0.0(3.1)
和
{
a
1
+
a
2
e
0.1
a
3
−
0.900
=
0.000
a
1
+
a
2
e
0.5
a
3
−
1.507
=
0.000
a
1
+
a
2
e
0.9
a
3
−
2.487
=
0.000
(3.4)
\left\{\begin{aligned} &a_1+a_2e^{0.1a_3}-0.900&=0.000\\ &a_1+a_2e^{0.5a_3}-1.507&=0.000\\ &a_1+a_2e^{0.9a_3}-2.487&=0.000\\ \end{aligned}\right.\tag{3.4}
⎩⎪⎨⎪⎧a1+a2e0.1a3−0.900a1+a2e0.5a3−1.507a1+a2e0.9a3−2.487=0.000=0.000=0.000(3.4)
的求解,显然后者很容易收敛,前者就很难,这就是所谓的要归一系数。
%% Problem 3
clear;
clc;
close all;
% initial_solution = [-328, 0.3, 0.0038];
% initial_solution = [-8.77989276139394,1.15049155426317e-08,0.0119755945151280];
initial_solution = [300, 1, 0.0001];
x = newtonsys(@f1, initial_solution);
initial_solution = [0, 1, 1];
x = newtonsys(@f2, initial_solution);
function [y,J] = f1(x)
y = [x(1) + x(2) * exp(1910 * x(3)) - 90.0;
x(1) + x(2) * exp(1950 * x(3)) - 150.7;
x(1) + x(2) * exp(1990 * x(3)) - 248.7;
];
J = [1, exp(1910 * x(3)), 1910 * x(2) * exp(1910 * x(3));
1, exp(1950 * x(3)), 1950 * x(2) * exp(1950 * x(3));
1, exp(1990 * x(3)), 1990 * x(2) * exp(1990 * x(3));
];
end
function [y,J] = f2(x)
y = [x(1) + x(2) * exp(0.1 * x(3)) - 0.900;
x(1) + x(2) * exp(0.5 * x(3)) - 1.507;
x(1) + x(2) * exp(0.9 * x(3)) - 2.487;
];
J = [1, exp(0.1 * x(3)), 0.1 * x(2) * exp(0.1 * x(3));
1, exp(0.5 * x(3)), 0.5 * x(2) * exp(0.5 * x(3));
1, exp(0.9 * x(3)), 0.9 * x(2) * exp(0.9 * x(3));
];
end
function x = newtonsys(f,x1)
% NEWTONSYS Newton's method for a system of equations.
% Input:
% f function that computes residual and Jacobian matrix
% x1 initial root approximation (n-vector)
% Output
% x array of approximations (one per column, last is best)
% Operating parameters.
funtol = 1000*eps; xtol = 1000*eps; maxiter = 40;
x = x1(:);
[y,J] = f(x1);
dx = Inf;
k = 1;
while (norm(dx) > xtol) && (norm(y) > funtol) && (k < maxiter)
dx = -(J\y); % Newton step
x(:,k+1) = x(:,k) + dx;
k = k+1;
[y,J] = f(x(:,k));
end
if k==maxiter, warning('Maximum number of iterations reached.'), end
05-03
- 4月25日的预言应验了,岁月也许终会磨平我的棱角罢。
- 刚好老舅一家来上海玩,下午去蹭个饭,缓释一下失恋的心情。
- 这次可能没有那么难受,也许我也开始慢慢开始习惯恋爱与失恋的滋味了,人总是要从理想慢慢走入现实的。
arnoldi迭代的matlab代码
function [Q,H] = arnoldi(A,u,m)
% ARNOLDI Arnoldi iteration for Krylov subspaces.
% Input:
% A square matrix (n by n)
% u initial vector
% m number of iterations
% Output:
% Q orthonormal basis of Krylov space (n by m+1)
% H upper Hessenberg matrix, A*Q(:,1:m)=Q*H (m+1 by m)
n = length(A);
Q = zeros(n,m+1);
H = zeros(m+1,m);
Q(:,1) = u/norm(u);
for j = 1:m
% Find the new direction that extends the Krylov subspace.
v = A*Q(:,j);
% Remove the projections onto the previous vectors.
for i = 1:j
H(i,j) = Q(:,i)'*v;
v = v - H(i,j)*Q(:,i);
end
% Normalize and store the new basis vector.
H(j+1,j) = norm(v);
Q(:,j+1) = v/H(j+1,j);
end
05-04
- 我以为真的是铁石心肠只用一天就完全能放下,结果做梦还是梦到她了。
- 事实上昨日且不说也妈妈聊了很多次,找人吃了饭,白天还跟wk通了70多分钟电话,最后今日午夜十二点半yy找我到宁远一楼当面聊了40多分钟,这可能是我这平生跟人说话时间最长的一天了,基本上是从乍暖还寒中缓过来了。
- 其实最关键的是最后午夜和yy的长聊,因为他得知的信息是最多的,yy也说最怕的就是恋爱中女孩嫌麻烦,他让我可以赶紧开始下一段,学习要学,恋爱也得谈。
- 最后一点半回寝完全睡不着,可能是白天一瓶咖啡效力太强,前天只睡了4个多小时,结果硬是写作业撑到凌晨三点,临睡前我想写一封邮件,但是实在太困了,怕会猝死,而且人应该有自制力,不应当纯凭欲望行事。那时候我突然意识到自己变了好多。因为昨晚回寝又发生了预料之外的事情,我是有点想去试试的,但是我觉得这样真的好渣,虽然已经不应该有所顾虑。总就是有这种荒谬的君子气节,我可能是不想被人诟病,包括被我自己诟病。
- 应该缓一缓,至少应该到这学期结束,我确实基本放下了,yy最后跟我说说不亏,白赚一首诗,笑死。回头看自己做事还是太草率了。
- 真心话,有yy和wk这两个真正的朋友,足矣,不枉我在这里待到第五年。
我感觉本文快要被封了,因为我废话确实写得太多,请审核手下留情,赶紧补一补正文:
本文字数已经达到上限,现在不能发长博文,估计快没了;
关于多项式插值:
这是个很有趣的问题,一般来说,插值点是均匀选取的,但是可能就会发生下面的情况

这个函数是
1
12
x
2
+
1
\frac1{12x^2+1}
12x2+11,在
[
−
1
,
1
]
[-1,1]
[−1,1]上均匀找差值点,结果就是会发现边缘拟合效果极差。
所以后来有人试着去创造新的插值方法,比较著名的就是切比雪夫点,
x i = − cos ( i π n ) 0 ≤ i ≤ n x_i=-\cos\left(\frac{i\pi}{n}\right)\quad0\le i\le n xi=−cos(niπ)0≤i≤n

可以发现拟合误差小了很多,此外其实还有一些别的拟合,一种比较有趣的是
c
u
b
i
c
s
p
l
i
n
e
i
n
t
e
r
p
o
l
a
n
t
\rm cubic\space spline\space interpolant
cubic spline interpolant,
matlab代码如下:这种插值是考虑到最多三阶导连续,所以会非常的平滑。
function S = spinterp(t,y)
% SPINTERP Cubic not-a-knot spline interpolation.
% Input:
% t interpolation nodes (vector, length n+1)
% y interpolation values (vector, length n+1)
% Output:
% S not-a-knot cubic spline (function)
t = t(:); y = y(:); % ensure column vectors
n = length(t)-1;
h = diff(t); % differences of all adjacent pairs
% Preliminary definitions.
Z = zeros(n);
I = eye(n); E = I(1:n-1,:);
J = I - diag(ones(n-1,1),1);
H = diag(h);
% Left endpoint interpolation:
AL = [ I, Z, Z, Z ];
vL = y(1:n);
% Right endpoint interpolation:
AR = [ I, H, H^2, H^3 ];
vR = y(2:n+1);
% Continuity of first derivative:
A1 = E*[ Z, J, 2*H, 3*H^2 ];
v1 = zeros(n-1,1);
% Continuity of second derivative:
A2 = E*[ Z, Z, J, 3*H ];
v2 = zeros(n-1,1);
% Not-a-knot conditions:
nakL = [ zeros(1,3*n), [1,-1, zeros(1,n-2)] ];
nakR = [ zeros(1,3*n), [zeros(1,n-2), 1,-1] ];
% Assemble and solve the full system.
A = [ AL; AR; A1; A2; nakL; nakR ];
v = [ vL; vR; v1; v2; 0 ;0 ];
z = A\v;
% Break the coefficients into separate vectors.
rows = 1:n;
a = z(rows);
b = z(n+rows); c = z(2*n+rows); d = z(3*n+rows);
S = @evaulate;
% This function evaluates the spline when called with a value for x.
function f = evaulate(x)
f = zeros(size(x));
for k = 1:n % iterate over the pieces
% Evalaute this piece's cubic at the points inside it.
index = (x>=t(k)) & (x<=t(k+1));
f(index) = polyval( [d(k),c(k),b(k),a(k)], x(index)-t(k) );
end
end
end
05-05
- 写了一封邮件,省得下次见面太尴尬。
- 昨晚一小时32圈,管他呢,腿废了就废了,省得再乱跑,反正是闲得蛋疼,正事不大做得进去,等明天上课见到活人再重整自己的节奏了,本来状态也不是很好,懒得逼自己放假做事。
- 《逝去日子》很好听,还挺合时宜的,晚上在图书馆单曲循环了一晚上,beyond的歌还是振奋,河图的听多了就像现在这样子颓唐。无论何意,很感谢这时候会有人来跟我说说话,或许也只是想找人说话了罢。经历挫伤之后人总是会变得谨慎。
-
matlab读取稀疏矩阵的问题:
一些大的稀疏矩阵,如果用csv存储矩阵形式是不现实的,所以可能要以稀疏形式存储,比如格式如下:
1,1,1 2,2,1 3,3,1 4,4,1上面其实存的是一个四阶的单位矩阵,那么matlab中其实是有办法直接读取的,但是一定要把格式调成上面的样子,间隔用逗号最好。
A = csvread('test.csv'); A = spconvert(A);这样其实就可以了,这次的问题是去用https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/regression.html的E2006 tfidf文件来做最小二乘的迭代算法,这个矩阵确实很大,直接算肯定是不行的,好在是稀疏矩阵,所以可以用这个方法来处理。
另外matlab中稀疏矩阵的转换是用
sparse(A)(转回来是full(A))
05-06
- 独自搞完下周一的pre的所有内容,下午我想想也省得麻烦再找ss和scx出来最后讨论一次了,虽然一个月前就已经准备好,让他们开始看起来,但是管科那边确实是忙,不指望他们能讲得多好。干脆所有的东西都我来讲,五一出事也没心情叫他们两个出来,到头来不如就自己一个人组队拉倒,还能在lth面前搞得潇洒点。
- 好闷的天,也不知道自己下周能不能讲好,唉,虽然可能我也不太在意能不能讲很好了。
- 下午还是躲在隔壁休息室,虽然这学期也便都是这样待在这儿的,但是… 总之就是烦。腿也伤了,要休整一段时间了。
凸规划灵敏度分析:
-
Perturbed Problem and its Dual
min f ( x ) s . t . g ( x ) ≤ u A x = b + v , x ∈ X \min f(x)\\ s.t.\quad g(x)\le u\\ Ax=b+v,x\in X minf(x)s.t.g(x)≤uAx=b+v,x∈X
其中 u ∈ R m , v ∈ R r u\in\R^m,v\in\R^r u∈Rm,v∈Rr;则写出对偶 q ~ ( μ , λ ) = q ( μ , λ ) − μ ⊤ u − λ ⊤ v \tilde q(\mu,\lambda)=q(\mu,\lambda)-\mu^\top u-\lambda^\top v q~(μ,λ)=q(μ,λ)−μ⊤u−λ⊤v
则对偶问题为: sup μ ≥ 0 q ~ ( μ , λ ) \sup_{\mu\ge0}\tilde q(\mu,\lambda) supμ≥0q~(μ,λ)
然后需要证明原问题和对偶问题的凸性;
全局敏感度分析结果
-
定理:假设原问题最优值有穷,且无dual gap,则对偶问题存在一个最优解 μ ∗ , λ ∗ \mu^*,\lambda^* μ∗,λ∗:
p ( u , v ) ≥ q ( μ ∗ , λ ∗ ) − μ ⊤ u ∗ − v ⊤ λ ∗ = p ( 0 , 0 ) − μ ⊤ u ∗ − v ⊤ λ ∗ p(u,v)\ge q(\mu^*,\lambda^*)-\mu^\top u^*-v^\top\lambda^*\\ =p(0,0)-\mu^\top u^*-v^\top\lambda^* p(u,v)≥q(μ∗,λ∗)−μ⊤u∗−v⊤λ∗=p(0,0)−μ⊤u∗−v⊤λ∗
敏感度推断:
- μ j ∗ \mu_j^* μj∗很大, p p p会快速增长若我们加紧约束 j j j( μ j < 0 \mu_j<0 μj<0);
- μ j ∗ \mu_j^* μj∗很小, p p p会缓缓增长若我们松弛约束 j j j( μ j > 0 \mu_j>0 μj>0);
- λ i ∗ \lambda_i^* λi∗很大且正, p p p会快速增长若我们选择 v i < 0 v_i<0 vi<0;
- λ i ∗ \lambda_i^* λi∗很大且负, p p p会快速增长若我们选择 v i > 0 v_i>0 vi>0;
- λ i ∗ \lambda_i^* λi∗很小且正, p p p会缓慢增长若我们选择 v i > 0 v_i>0 vi>0;
- λ i ∗ \lambda_i^* λi∗很小且负, p p p会缓慢增长若我们选择 v i < 0 v_i<0 vi<0;
局部敏感度:
-
定理:假设原问题最优值有穷,且无dual gap,则对偶问题存在一个最优解 μ ∗ , λ ∗ \mu^*,\lambda^* μ∗,λ∗,且原问题值函数在 ( 0 , 0 ) (0,0) (0,0)处可微:
μ j ∗ = − ∂ p ( 0 , 0 ) ∂ u j , λ i ∗ = − ∂ p ( 0 , 0 ) ∂ v i \mu_j^*=-\frac{\partial p(0,0)}{\partial u_j},\lambda_i^*=-\frac{\partial p(0,0)}{\partial v_i} μj∗=−∂uj∂p(0,0),λi∗=−∂vi∂p(0,0)
敏感度推断:
- 若 g j ( x ∗ ) < 0 g_j(x^*)<0 gj(x∗)<0(inactive constraints),则 μ j ∗ = 0 \mu_j^*=0 μj∗=0,因此约束 g j g_j gj可以被加紧或松弛一点,而不会影响最优值 f ∗ f^* f∗;
- 若 g j ( x ∗ ) = 0 g_j(x^*)=0 gj(x∗)=0,且 μ j \mu_j μj小,则加紧或缩小约束对 f ∗ f^* f∗影响很小;
- 若 g j ( x ∗ ) = 0 g_j(x^*)=0 gj(x∗)=0,且 μ j \mu_j μj大,则加紧或缩小约束对 f ∗ f^* f∗影响很大;
-
05-07
- Eviews大坑,晚上跟lth两个菜逼下课搞到9点也不知道搞得对不对,不知道经院那边是不是这玩意儿用得比较熟… 这学期计量和时间序列是真的两个深坑,学这么多有个毛用,不知道哪来这么多东西要检验。
- 日子逐渐开始恢复平静,似乎也不会发生什么所预想的事情。学习,跑步,吃饭,睡觉,写日记,想玩就玩一会儿。腿已经基本恢复,开始冲四分配,保持住状态,下半年去跑半马。
Error:字数溢出,停更。

























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








