目录
回顾
稍微回顾一下LTL与公平性相关的知识
我们知道,在LTL上的公平性约束可以表示为
设 ϕ \phi ϕ和 ψ \psi ψ是命题公式:
- 无条件的公平性: □ ◊ ψ \Box\Diamond\psi □◊ψ
- 强公平性: □ ◊ ϕ → □ ◊ ψ \Box\Diamond\phi\rightarrow\Box\Diamond\psi □◊ϕ→□◊ψ
- 弱公平性: ◊ □ ϕ → □ ◊ ψ \Diamond\Box\phi\rightarrow\Box\Diamond\psi ◊□ϕ→□◊ψ
并且,在LTL上添加公平性约束,并不会影响我们的对LTL的模型检测,因为我们推导了结论:
s
⊨
f
a
i
r
ϕ
当且仅当 对于所有的π∈Paths(s),如果
π
⊨
f
a
i
r
,
那
么
π
⊨
ϕ
当且仅当
s
⊨
(
f
a
i
r
→
ϕ
)
s\vDash_{fair}\phi \\ \text{当且仅当 对于所有的π∈Paths(s),如果}π\vDash fair,那么π\vDash\phi \\ \text{当且仅当 }s\vDash (fair\rightarrow\phi)
s⊨fairϕ当且仅当 对于所有的π∈Paths(s),如果π⊨fair,那么π⊨ϕ当且仅当 s⊨(fair→ϕ)
看到 s ⊨ ( f a i r → ϕ ) s\vDash (fair\rightarrow\phi) s⊨(fair→ϕ)这个地方,假设我们的公平性假设现在是fair= ◊ □ a \Diamond\Box\ a ◊□ a,那么可满足性就变成了 s ⊨ ( ◊ □ ¬ a ∨ ϕ ) s\vDash (\Diamond\Box\lnot a\vee\phi) s⊨(◊□¬a∨ϕ),这边是个 ∨ \vee ∨的关系,所以模型检测算法可以直接用在具有公平性约束的LTL上。
前面有一张对比LTL和CTL的表,我们也知道了如果CTL具有公平性约束,就不会像LTL那么简单了,需要额外的技术进行操作,那么接下来慢慢看吧。
CTL公平性约束
其实形式上的话和LTL的公平性约束公式有点像,不过CTL要考虑所有路径的状况
unconditional CTL fairness定义为:
u
f
a
i
r
=
⋀
1
≤
i
≤
k
□
◊
ψ
i
ufair=\bigwedge_{1≤i≤k}\Box\Diamond\psi_{i}
ufair=1≤i≤k⋀□◊ψi
strong CTL fairness的形式为:
s
f
a
i
r
=
⋀
1
≤
i
≤
k
(
□
◊
ψ
i
→
□
◊
ϕ
i
)
sfair=\bigwedge_{1≤i≤k}(\Box\Diamond\psi_{i}\rightarrow\Box\Diamond\phi_{i})
sfair=1≤i≤k⋀(□◊ψi→□◊ϕi)
weak CTL fairness定义为:
w
f
a
i
r
=
⋀
1
≤
i
≤
k
(
◊
□
ψ
i
→
□
◊
ϕ
i
)
wfair=\bigwedge_{1≤i≤k}(\Diamond\Box\psi_{i}\rightarrow\Box\Diamond\phi_{i})
wfair=1≤i≤k⋀(◊□ψi→□◊ϕi)
其中 ψ i , ϕ i \psi_{i},\phi_{i} ψi,ϕi是CTL状态公式
CTL公平性假设fair定义和公平性假设定义类似,就是ufair,sfair,wfair上面三者的结合
CTL公平性假设的语义
- s ⊨ f a i r t r u e s\vDash_{fair} true s⊨fairtrue
- s ⊨ f a i r a s\vDash_{fair} a s⊨faira当且仅当 a∈Label(s)
- s ⊨ f a i r φ 1 ∧ φ 2 s\vDash_{fair} φ_{1}\wedge φ_{2} s⊨fairφ1∧φ2当且仅当 ( s ⊨ f a i r φ 1 ) ∨ ( s ⊨ f a i r φ 2 ) (s\vDash_{fair} φ_{1})\vee (s\vDash_{fair} φ_{2}) (s⊨fairφ1)∨(s⊨fairφ2)
- s ⊨ f a i r ¬ φ s\vDash_{fair} \lnotφ s⊨fair¬φ 当且仅当 ¬ ( s ⊨ f a i r φ ) \lnot(s\vDash_{fair} φ) ¬(s⊨fairφ)
- s ⊨ f a i r ∃ φ s\vDash_{fair} \existφ s⊨fair∃φ 当且仅当 存在从s开始的公平性路径满足 s ⊨ f a i r φ s\vDash_{fair}φ s⊨fairφ
- s ⊨ f a i r ∀ φ s\vDash_{fair} \forallφ s⊨fair∀φ 当且仅当 对于所有从s开始的公平性路径满足 s ⊨ f a i r φ s\vDash_{fair}φ s⊨fairφ
- s ⊨ f a i r ◯ φ s\vDash_{fair} \bigcircφ s⊨fair◯φ 当且仅当 π [ 1 ] ⊨ f a i r φ \pi[1]\vDash_{fair}φ π[1]⊨fairφ
- s ⊨ f a i r φ 1 U φ 2 s\vDash_{fair} φ_{1}Uφ_{2} s⊨fairφ1Uφ2 当且仅当 存在 j ≥ 0 j\ge0 j≥0使得 π [ j ] ⊨ f a i r φ 2 ∧ ( ∀ 0 ≤ k < j . π [ k ] ⊨ f a i r φ 1 ) \pi[j]\vDash_{fair}φ_{2}\wedge(\forall0\le k\lt j.\pi[k]\vDash_{fair}φ_{1}) π[j]⊨fairφ2∧(∀0≤k<j.π[k]⊨fairφ1)
带有公平性假设的CTL模型检测问题
给定一个TS模型,给定一个CTL公式 ϕ \phi ϕ,它的形式为ENF,并且给定一个CTL上的公平性假设fair,如何判断 T S ⊨ f a i r ϕ TS\vDash_{fair} \phi TS⊨fairϕ是否成立?
其实和LTL最不同的处理方式就是:
通过忽略不公平路径的方式来改变CTL公式的语义
算法主要流程不变:
- 递归地计算 S a t ( ϕ ) = { s ∈ S ∣ s ⊨ ϕ } Sat(\phi)=\{s\in S|s\vDash\phi\} Sat(ϕ)={s∈S∣s⊨ϕ}
- 检查是不是所有的初始状态都属于 S a t ( ϕ ) Sat(\phi) Sat(ϕ),即 S 0 ⊆ S a t ( ϕ ) S_{0}\subseteq Sat(\phi) S0⊆Sat(ϕ)
但是可满足集的计算方式部分发生了变化
1、不发生变化的部分
- S a t f a i r ( t r u e ) = S Sat_{fair}(true)=S Satfair(true)=S
- S a t f a i r ( a ) = { s ∈ S ∣ a ∈ L ( s ) } Sat_{fair}(a)=\{s\in S|a\in L(s)\} Satfair(a)={s∈S∣a∈L(s)},对于任意a∈AP
- S a t f a i r ( ϕ ∧ ψ ) = S a t f a i r ( ϕ ) ∩ S a t f a i r ( ψ ) Sat_{fair}(\phi\wedge\psi)=Sat_{fair}(\phi)\cap Sat_{fair}(\psi) Satfair(ϕ∧ψ)=Satfair(ϕ)∩Satfair(ψ)
- S a t f a i r ( ¬ ϕ ) = S ∖ S a t f a i r ( ϕ ) Sat_{fair}(\lnot\phi)=S\setminus Sat_{fair}(\phi) Satfair(¬ϕ)=S∖Satfair(ϕ)
2、发生部分变化的部分
- S a t f a i r ( ∃ ◯ ϕ ) = S a t ( ∃ ◯ ( ϕ ∧ a f a i r ) ) Sat_{fair}(\exist\bigcirc\phi)=Sat(\exist\bigcirc(\phi\wedge a_{fair})) Satfair(∃◯ϕ)=Sat(∃◯(ϕ∧afair))
- S a t f a i r ( ∃ ϕ U ψ ) = S a t ( ∃ ( ϕ U ( ψ ∧ a f a i r ) ) ) Sat_{fair}(\exist \phi U\psi)=Sat(\exist(\phi U(\psi\wedge a_{fair}))) Satfair(∃ϕUψ)=Sat(∃(ϕU(ψ∧afair)))
这个
a
f
a
i
r
a_{fair}
afair是一个额外添加的原子命题,它的含义是
a
f
a
i
r
∈
L
(
s
)
当
且
仅
当
s
⊨
f
a
i
r
∃
□
t
r
u
e
a_{fair}\in L(s)当且仅当s\vDash_{fair}\exist\Box true
afair∈L(s)当且仅当s⊨fair∃□true
自然语言表述一下就是把不公平的部分排除在外不进行考虑, 根据例子来看看这个 a f a i r a_{fair} afair是怎么把不公平路径排掉的
例如我们有这么一个TS系统
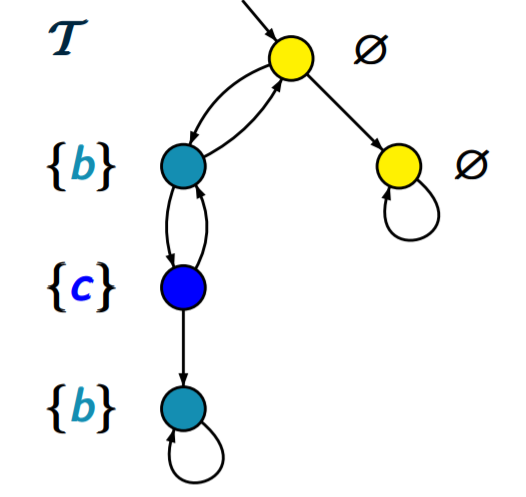
给定一个CTL公式
∃
◊
c
\exist\Diamond c
∃◊c,给定一个strong fair:
f
a
i
r
=
□
◊
b
→
□
◊
c
fair=\Box\Diamond b\rightarrow\Box\Diamond c
fair=□◊b→□◊c
然后,因为这个CTL公式带有了公平性假设的约束,所以我们只考虑满足公平性假设的情况,而不考虑不满足公平性假设的情况,所以原始的CTL公式变化为 ∃ ◊ ( c ∧ a f a i r ) \exist\Diamond (c\wedge a_{fair}) ∃◊(c∧afair)
我们可以看到虚线上面的状态都是满足这个公平性假设,而唯独最下面的那个状态不满足,我们就把它排除掉。
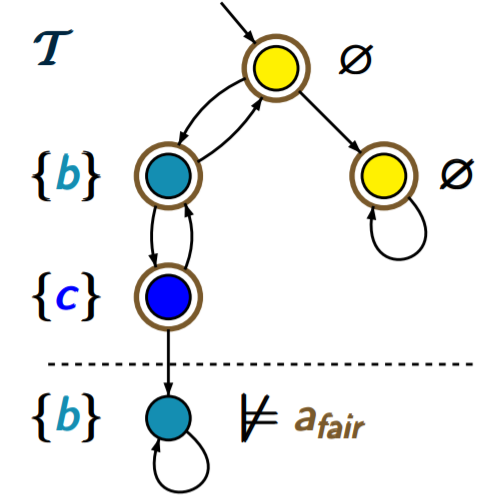
最后
(
c
∧
a
f
a
i
r
)
(c\wedge a_{fair})
(c∧afair)指的就是下图中蓝色圆圈的状态

通过加入命题公式
a
f
a
i
r
a_{fair}
afair的方式,我们用形式化的方式将不公平路径从考虑中排除,然后就按照计算Sat方式就可以完成计算了。
其中这两部分和纯CTL的模型检测还是很相似的,不过一旦CTL公式是类似于 ∃ □ a \exist\Box a ∃□a这样子的话,上面的方式就没啥用了,所以对于 ∃ □ a \exist\Box a ∃□a需要重新定义算法
3、需要重新定义算法的部分( ∃ □ a \exist\Box a ∃□a)
这个部分我们就是要计算
S
a
t
f
a
i
r
(
∃
□
a
)
Sat_{fair}(\exist\Box a)
Satfair(∃□a)这个特例,怎么算呢?分为三步:
1、在TS上除去那些
s
⊭
a
s\nvDash a
s⊭a的状态,获得一个子图
2、找找看子图上是否存在满足公平性的状态所组成的环,并使得从初始状态
s
0
s_{0}
s0出发可以达到这个环
3、所有环上的状态以及可以到达这个环的状态组成的集合就是
S
a
t
f
a
i
r
(
∃
□
a
)
Sat_{fair}(\exist\Box a)
Satfair(∃□a)的值
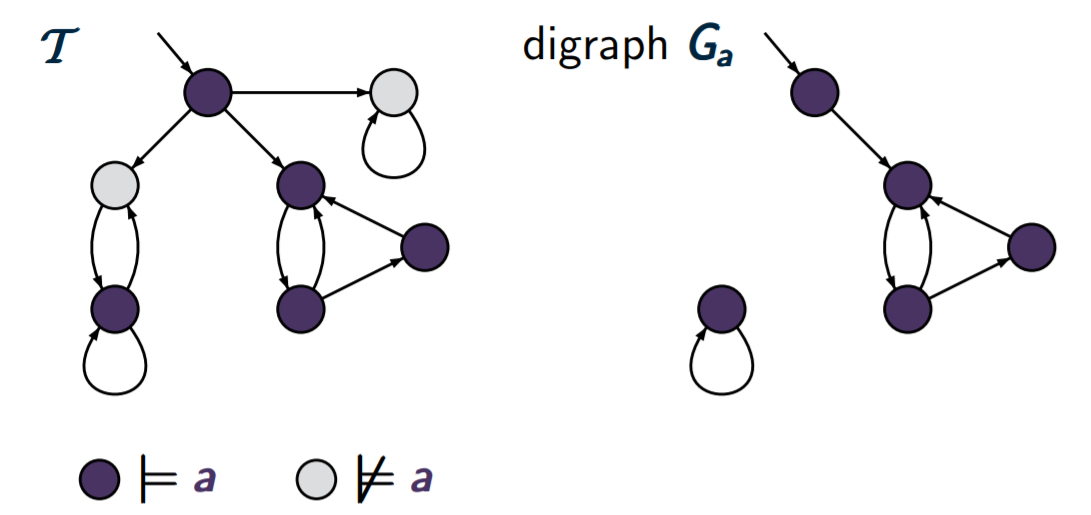
来看一个例子,假设我们有这么一个TS,CTL公式为 ∃ □ a \exist\Box a ∃□a, s ⊨ a s\vDash a s⊨a和 s ⊭ a s\nvDash a s⊭a的部分都标出来了,我们按照第一步先把 s ⊭ a s\nvDash a s⊭a的状态都删了,得到右边那一张子图
现有公平性假设为
f
a
i
r
=
(
□
◊
b
1
→
□
◊
c
1
)
∧
(
□
◊
b
2
→
□
◊
c
2
)
fair=(\Box\Diamond b_{1}\rightarrow \Box\Diamond c_{1})\wedge (\Box\Diamond b_{2}\rightarrow \Box\Diamond c_{2})
fair=(□◊b1→□◊c1)∧(□◊b2→□◊c2)
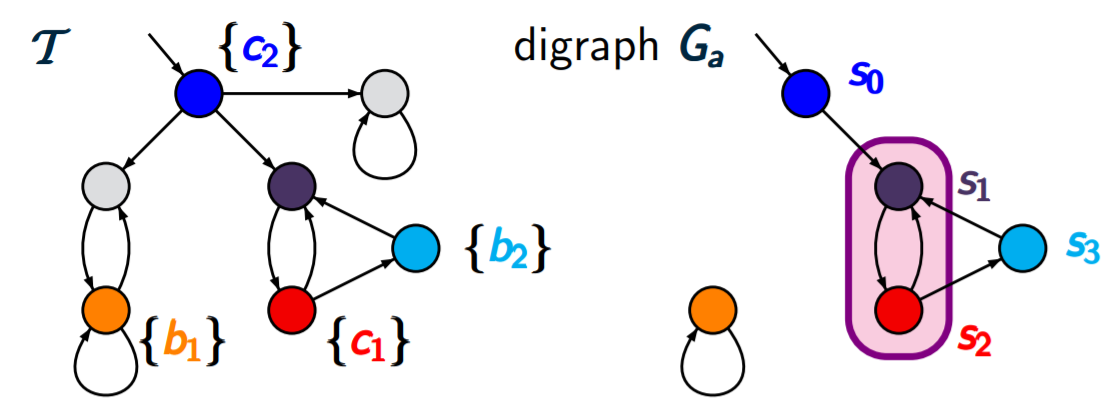
我们看看这个子图里面,是否有满足公平性的状态组成的环,我们现在找到一个环由
s
1
s_{1}
s1和
s
2
s_{2}
s2组成,并且它们满足公平性,我们看到
s
0
s_{0}
s0是初始状态可以到达这个环,而
s
3
s_{3}
s3也可以到达这个环,所以
S
a
t
f
a
i
r
(
∃
□
a
)
=
{
s
0
,
s
1
,
s
2
,
s
3
}
Sat_{fair}(\exist\Box a)=\{s_{0},s_{1},s_{2},s_{3}\}
Satfair(∃□a)={s0,s1,s2,s3}
至此我们解决了带有公平性假设的CTL模型检测问题
时间复杂度
假设TS带有N个状态和M个转换,假设公平性假设由k个约束组成
那么解决带有公平性假设约束的CTL公式
ϕ
\phi
ϕ的模型检测问题的时间复杂度为:
O
(
∣
ϕ
∣
⋅
(
M
+
N
)
⋅
k
)
O(|\phi|·(M+N)·k)
O(∣ϕ∣⋅(M+N)⋅k)
























 1101
1101











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








