公平性(Fairness)
系统的一个重要方面是公平性,公平性排除了被认为是不现实(unrealistic)的无限行为,并且这一步通常是建立活性属性所必需的。
我们通过在并发系统中经常遇到的一个问题来说明公平的概念:
现有一个并发系统N,有进程 P 1 , P 2 . . . P N P_{1},P_{2}...P_{N} P1,P2...PN,它们在有需要时就会请求服务,但是现在只有一个服务进程名叫Server会为这些进程提供服务,现在Server采用如下策略:从P1开始检查,如果P1请求了服务,那么就为P1提供服务,如果P1没有请求,那么就检查下一个进程P2,直到检查完毕,然后从头开始检查。我们可以想见,如果P1一直请求服务,那么Server会为P1无限次提供服务,而剩下的进程都会陷入无限等待的过程,这对除P1外的进程来说是是不公平(unfair)的,这种行为就属于不现实的无限行为。
为了获得由TS建模的并行系统的行为的真实描述,我们需要一种另一种形式的LT属性,来解决TS中不确定性决策的问题。
于是,为了排除上述不现实的行为,我们需要添加公平性约束(Fairness Constraints),而公平的执行或者轨迹(execute or trace)就是满足了某些公平性约束。
基于动作的公平性约束
如何表述这类公平性约束?这里采用基于动作(action)的观点(还有基于状态的公平,不在这里讨论)
对于一个没有终止状态的 T S = ( S , A c t , → , S 0 , A P , L ) TS=(S, Act,→,S_{0}, AP, L) TS=(S,Act,→,S0,AP,L),A⊆ Act,TS上的无限执行片段 ρ = s 0 → α 0 s 1 → α 1 . . . ρ =s_{0}\xrightarrow{α_{0}} s_{1}\xrightarrow{α_{1}}... ρ=s0α0s1α1...,公平约束具有三风格:
- 如果ρ是unconditionally A-fair,那么无论何时
if ∃ ∞ j ≥ 0 , a j ∈ A . \text{if }\overset{∞}\exist j\ge 0,a_{j}∈A. if ∃∞j≥0,aj∈A.
无条件A-fair的含义是,无论在什么情况下,A中的动作总能无限经常次执行。
- 如果ρ是strongly A-fair,那么无论何时
( ∃ ∞ j . A c t ( s j ∩ A ≠ ∅ ) ⇒ ( if ∃ ∞ j ≥ 0 , a j ∈ A ) (\overset{∞}\exist j.Act(s_{j}\cap A\ne ∅)\Rightarrow(\text{if }\overset{∞}\exist j\ge 0,a_{j}∈A) (∃∞j.Act(sj∩A=∅)⇒(if ∃∞j≥0,aj∈A)
strongly A-fair的含义是,存在无限经常次A为enabled时,A中动作将会无限经常次执行。
- 如果ρ是weakly A-fair,那么无论何时
( ∀ ∞ j . A c t ( s j ∩ A ≠ ∅ ) ⇒ ( if ∃ ∞ j ≥ 0 , a j ∈ A ) (\overset{∞}\forall j.Act(s_{j}\cap A\ne ∅)\Rightarrow(\text{if }\overset{∞}\exist j\ge 0,a_{j}∈A) (∀∞j.Act(sj∩A=∅)⇒(if ∃∞j≥0,aj∈A)
weakly A-fair的含义是,从某个时刻起,A将会为enabled,从而A中动作将会无限经常次执行。
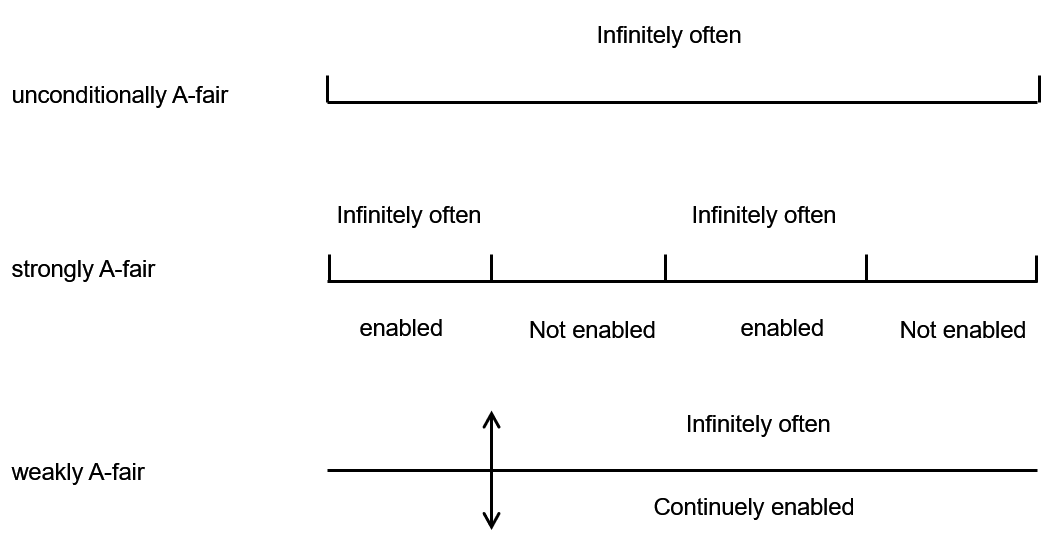
定义什么的太难懂了,来点直白点的解释,无条件就是任何时候都是无限经常次执行的
strong和weak这俩引入了enabled这个概念,strongly A-fair要求在enable的片段中动作能够无限经常次执行,而在not enabled的片段中没有规定
weakly A-fair则是,不管之前如何,如果在某一个时间点之后,动作持续一直enabled,那么在这片段中动作要求能够无限经常次执行
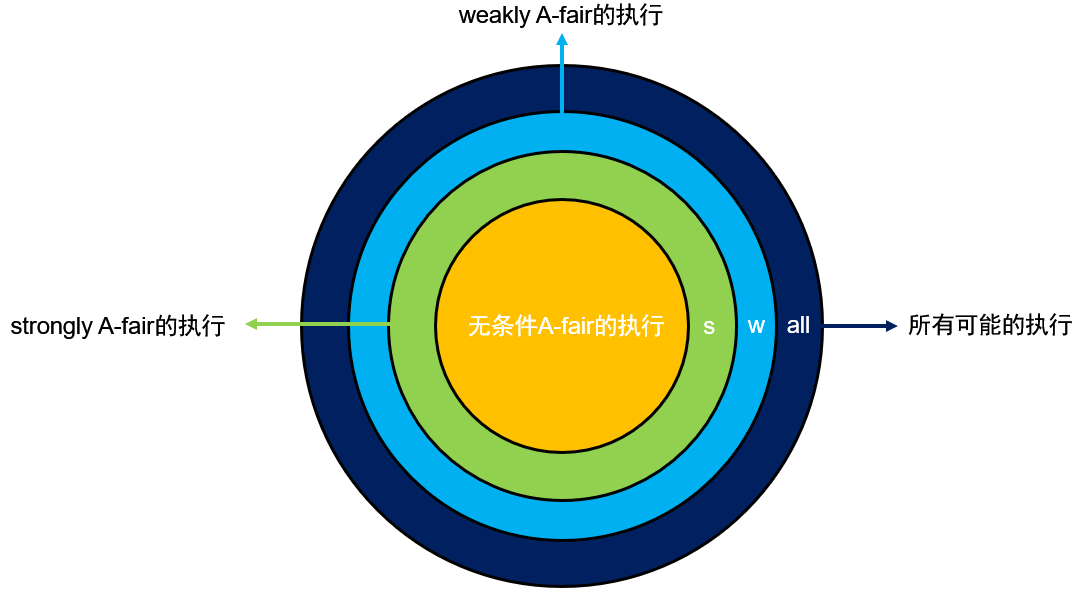
从上面的定义中我们可以容易得到
unconditionally A-fair
⇒
strongly A-fair
⇒
weakly A-fair
\text{unconditionally A-fair}\Rightarrow \text{strongly A-fair}\Rightarrow \text{weakly A-fair}
unconditionally A-fair⇒strongly A-fair⇒weakly A-fair
例题
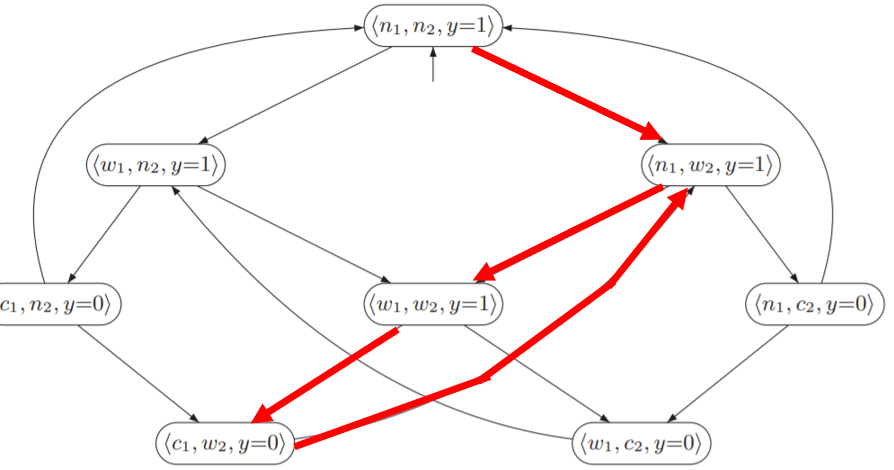
看看这张两个进程互斥进入临界区的图
设A={enter1}
对于上面这条红色路径来说,它是哪种A-fair?
unconditionally A-fair。因为动作只有enter1,我们只需考虑这一个动作,enter1就是进程1进入临界区,我们看到红色路径中无限经常次执行enter1,没有任何条件(当然你也可以说这是strongly A-fair和weakly A-fair,因为这几个是包含关系)
设A={enter2}
对于上面这条红色路径来说,它是哪种A-fair?
weakly A-fair。首先它肯定不是无条件的,其次在考虑一下strong,观察状态<w1.w2.y=1>这个时候,进程2属于enabled状态,因为它能够执行该动作,但是它执行(即进入临界区)了吗?没有,所以在enabled的时候它没有无限经常次执行动作,所以它不是strong,最后是weak,它压根就没有在某一个时间点后能够持续的enabled,因为进入<c1,w2,y=0>这个状态对进程2来说就是not enabled,所以它属于weakly A-fair
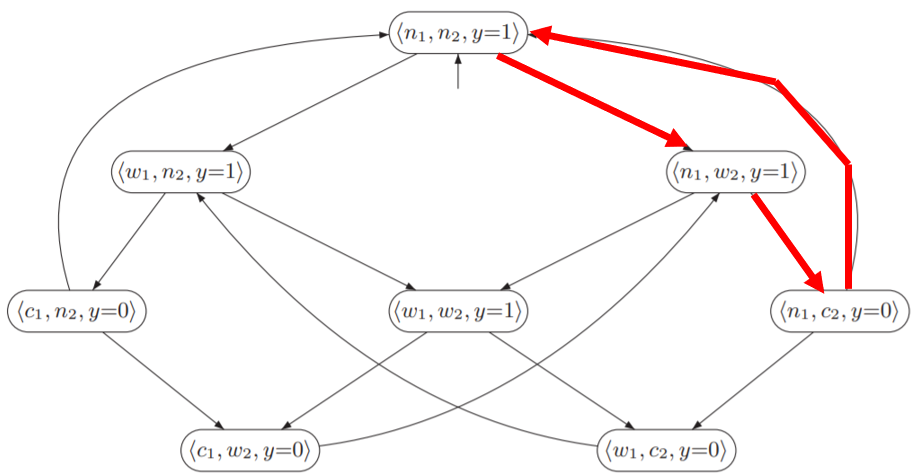
设A={enter1}
对于上面这条红色路径来说,它是哪种A-fair?
strongly A-fair。可以看到,这个执行序列是进程2一直在进入临界区,进程1一直在等待,所以肯定不是无条件的,但是满足strongly的定义,因为strongly要求在endabled时能够无限经常次进入,进程1根本现在没有enabled的状态,所以是strongly A-fair,当然也是weakly。
设A={enter1,enter2}
对于上面这条红色路径来说,它是哪种A-fair?
unconditionally A-fair
让我们来看看定义
if
∃
∞
j
≥
0
,
a
j
∈
A
.
\text{if }\overset{∞}\exist j\ge 0,a_{j}∈A.
if ∃∞j≥0,aj∈A.
只要存在一个动作满足无限经常次执行就可以了,所以enter2在无限经常次执行,它就是无条件的。
公平性假设(fairness assumption)
有时候我们定义公平性可能要用到不止一种风格的公平性约束,一般要考虑到三种风格,这就有了公平性假设这个概念
我们定义公平性假设为一个三元组
F
=
(
F
u
c
o
n
d
,
F
s
t
r
o
n
g
,
F
w
e
a
k
)
F=(F_{ucond},F_{strong},F_{weak})
F=(Fucond,Fstrong,Fweak)
F u c o n d , F s t r o n g , F w e a k ⊆ 2 A c t F_{ucond},F_{strong},F_{weak}\subseteq 2^{Act} Fucond,Fstrong,Fweak⊆2Act,这表示这三个F是集合的集合,类似于 F u c o n d = { A 1 , A 2 } , A 1 = { e n t e r 1 } , A 2 = { e n t e r 1 , e n t e r 2 } F_{ucond}=\{A_{1},A_{2}\},A_{1}=\{enter1\},A_{2}=\{enter1,enter2\} Fucond={A1,A2},A1={enter1},A2={enter1,enter2}
如果 ρ ρ ρ被称为F-fair,那么:
- 对所有 A ∈ F u c o n d A∈F_{ucond} A∈Fucond,ρ是unconditionally A-fair
- 对所有 A ∈ F s t r o n g A∈F_{strong} A∈Fstrong,ρ是strongly A-fair
- 对所有 A ∈ F w e a k A∈F_{weak} A∈Fweak,ρ是weakly A-fair
公平轨迹定义为:
F
a
i
r
T
r
a
c
e
s
F
(
T
S
)
=
{
t
r
a
c
e
(
ρ
)
:
ρ
是
T
S
上
的
F
−
f
a
i
r
执
行
}
FairTraces_{F}(TS)=\{trace(ρ):ρ是TS上的F-fair执行\}
FairTracesF(TS)={trace(ρ):ρ是TS上的F−fair执行}
例:
考虑到两进程互斥模型有如下的公平性需求:
each waiting process eventually enters its critical section
每个等待的进程最终会进入临界区
首先我们考虑不加约束的情况下,它能够满足嘛?显然是不行的
现在我们为其加入公平性假设
F
s
t
r
o
n
g
=
F
u
c
o
n
d
=
∅
F
w
e
a
k
=
{
{
e
n
t
e
r
1
}
,
{
e
n
t
e
r
2
}
}
F_{strong}=F_{ucond}=∅ \\ F_{weak}=\{\{enter1\},\{enter2\}\}
Fstrong=Fucond=∅Fweak={{enter1},{enter2}}
加入了这个约束之后,能够满足公平性了嘛?
还是不行,这个在上面的例子中有讲到,搬出这张图

这个路径是满足weakly的公平性约束的,但是进程2还是不能进入临界区
接着再考虑一下strongly的约束,现在约束改为:
F
w
e
a
k
=
F
u
c
o
n
d
=
∅
F
s
t
r
o
n
g
=
{
{
e
n
t
e
r
1
}
,
{
e
n
t
e
r
2
}
}
F_{weak}=F_{ucond}=∅ \\ F_{strong}=\{\{enter1\},\{enter2\}\}
Fweak=Fucond=∅Fstrong={{enter1},{enter2}}
现在,嗯,将约束放到strong下后,我们可以发现现在是满足这个公平性的了。
好,回顾一下刚刚那个过程,我们从构建公平性假设的时候,先看看需不需要加入公平性约束,如果需要,应该从weakly A-fair开始,因为我们要做的是排除那些不符合要求的路径,要做到排除的路径尽可能的少,又要满足相应的要求,所以先从一般性情况出发,先考虑weakly再考虑strongly最后再考虑unconditionally。
现在我们有新的公平性需求了,在原有的基础上加入每个进程无限经常次进入临界区的要求
each waiting process eventually enters its critical section
每个等待的进程最终会进入临界区
each process enter to critical section infinitely often
每个进程将会无限经常次进入临界区
来看看这个现在的情况满不满足要求呢?NO
同样回到上面的例子

这种情况虽然满足strong的约束,但是不符合公平性要求
现在仍然从weakly开始考虑,将约束改为
F u c o n d = ∅ F w e a k = { { r e q 1 } , { r e q 2 } } F s t r o n g = { { e n t e r 1 } , { e n t e r 2 } } F_{ucond}=∅ \\ F_{weak}=\{\{req1\}, \{req2\}\} \\ F_{strong}=\{\{enter1\},\{enter2\}\} Fucond=∅Fweak={{req1},{req2}}Fstrong={{enter1},{enter2}}
req表示进程进入等待区的过程,为什么加入了这个weak约束,它就能满足无限次进入临界区的公平性了呢?也就是说,我们加了这个约束之后,它排除了如上图的循环,如何排除的?
我们以上图为例仔细看看, < n 1. n 2 , y = 1 > → < n 1 , w 2 , y = 1 > → < n 1. c 2. y = 0 > <n1.n2,y=1>\rightarrow<n1,w2,y=1>\rightarrow<n1.c2.y=0> <n1.n2,y=1>→<n1,w2,y=1>→<n1.c2.y=0>,在这三个状态时,我们都可以走图中左边的那条路吧,而这三个状态走另一条要执行的动作均为req1,也就是说进程1一直处于一种enabled状态,但却又没有执行req1,这就违反了了weakly约束在一个持续的enabled序列中要求无限经常次执行动作req1的约束,所以这条路就这么被排除了。
所以,这样的一个公平性假设满足了我们提出的公平性要求。
公平性的满足
回想一下,如果一个TS满足线性时间属性P,那么可以表示为
T
S
⊨
P
当且仅当
T
r
a
c
e
s
(
T
S
)
⊆
P
TS \vDash P\text{ 当且仅当}Traces(TS) ⊆ P
TS⊨P 当且仅当Traces(TS)⊆P
类似的,我们将TS在公平假设F下,满足线性时间属性P表示为
T
S
⊨
F
P
当
且
仅
当
F
a
i
r
T
r
a
c
e
s
F
(
T
S
)
⊆
P
TS \vDash_{F}P当且仅当FairTraces_{F}(TS)⊆P
TS⊨FP当且仅当FairTracesF(TS)⊆P
可实现的公平性与安全性
如果公平性假设F对一个TS来说是可实现的(realizable),那么对于TS上的每一个可达状态s,均存在从s开始的F-fair路径
可实现的公平性与安全性之间的关系有这么一个结论:
可实现的公平性假设和安全性是不相关的
想象一下之前那个线性时间属性的分类图,可实现的公平性和其他部分(非安全性)是相关的,但是和安全性是不相关的。
这里的不相关可能有些难理解,假如我们有一个TS,它满足一个安全性,现在加入一个公平性假设F,这个TS系统在这个公平性假设F的约束下,仍然满足安全性
也就是说
T
S
⊨
P
s
a
f
e
当
且
仅
当
T
S
⊨
F
P
s
a
f
e
TS\vDash P_{safe} 当且仅当 TS\vDash_{F} P_{safe}
TS⊨Psafe当且仅当TS⊨FPsafe
























 785
785











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








