椭圆曲线加法运算(二)

1. 椭圆曲线加法运算

1.1. 问题描述

给定椭圆曲线$y^2=x^3+8$，点P=$(1,3)$，求P+P=?

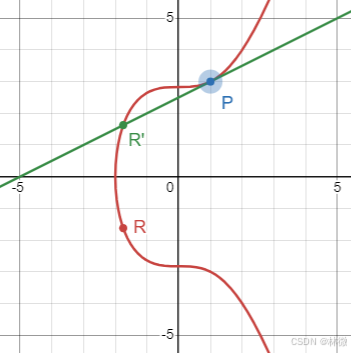
[图片来自: https://www.desmos.com/calculator/fttnxuzryp?lang=zh-TW]

1.2. 解决方案

步骤一: 计算椭圆曲线$y^2=x^3+8$在P点的切线的方程

对椭圆曲线的隐函数在x，y方向上分别求导，有，
$2ydy=3x^{2}dx$
$\frac{dy}{dx}=\frac{3x^2}{2y}=\frac{1}{2}$

代入P点，得到过P点切线的方程
$y=\frac{1}{2}x+\frac{5}{2}$

步骤二: 计算切线方程与椭圆曲线的第三个交点

联立切线方程和椭圆曲线，得到，
$\{\begin{array}{ll}y=\frac{1}{2}x+\frac{5}{2}& \\ y^2=x^3+8& \end{array}$

切线方程代入椭圆曲线，得到，
${\left(\frac{1}{2}x+\frac{5}{2}\right)}^2=x^3+8$
$4x^3-x^2-10x+7=0$
$\left(x-1\right)\cdot \left(4x-4\right)\cdot \left(x+\frac{7}{4}\right)=0$

得到第三个交点： $R^{\prime }=\left(-\frac{7}{4},\frac{\sqrt{169}}{8}\right)$

即，P+P=R=$\left(-\frac{7}{4},-\frac{\sqrt{169}}{8}\right)$

参考资料

[1. 椭圆曲线的加法运算] https://www.ruanx.net/elliptic-curve/
[2. 椭圆曲线的加法运算] https://zh.wikipedia.org/zh-cn/%E6%A9%A2%E5%9C%93%E6%9B%B2%E7%B7%9A%E7%9A%84%E7%B4%94%E9%87%8F%E4%B9%98%E6%B3%95