第三章:线性回归回顾
本章是是一些比较基础的数学问题,主要是在后面章节案例中引入多特征时所必须掌握的基本数学技巧,所以吴老师在第三章带我们一起回顾了些;这里我就不做过多总结和分享,只列举一些基本知识点概念,作为学习笔记;
1、矩阵(matrix)、向量(vector)
矩阵是由数字组成的矩形阵列,并写在大方括号里,如:,这是一个2x3的矩阵;向量是一个比较特殊的矩阵,它只有一列,即一个nx1的矩阵被称为向量,如:
,这是一个向量,也是一个3×1的矩阵;这里给出一个维度的概念,即一个2行3的矩阵我们就说它的维度是2×3; 我们可以用一个字母加上标的形式表达一个特定维度的矩阵,如:
 表示矩阵R有n行m列,用字母加下标表示其中一个特定的元素,如:
表示矩阵R有n行m列,用字母加下标表示其中一个特定的元素,如: 表示矩阵A中第i行第j列的元素;
表示矩阵A中第i行第j列的元素;
2、矩阵的加减法
只有维度相同的矩阵才能进行加减法;计算公式为: ,即两个矩阵对应元素进行加减,例如:
,即两个矩阵对应元素进行加减,例如:
3、矩阵的乘法
矩阵相乘时他们的维度必须满足如下公式: ,矩阵中的元素满足公式:
,矩阵中的元素满足公式:;例如:
4、单位矩阵( )、以及矩阵的逆(
)、以及矩阵的逆(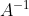 )和转置(
)和转置(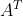 )
)
单位矩阵 对角线上的元素都为1,其余元素都为零,它满足如下关系:
对角线上的元素都为1,其余元素都为零,它满足如下关系: (可类比单位1)
(可类比单位1)
矩阵和它的逆矩阵满足如下关系: ,部分矩阵不存在逆矩阵;(可类比倒数)
,部分矩阵不存在逆矩阵;(可类比倒数)
矩阵的转置是将矩阵中的元素沿对角线对称互换位置获得,他们之间的元素满足如下关系: ;
;
5、矩阵的除法
一般不说矩阵的除法,通常都是讲的矩阵求逆 如: ;
;
最后这里我们给一个矩阵相乘的实际用涂,在前一章节的背景下有一个目标函数和m个样本
,我们用一个m×2的矩阵包涵所有样本:
,用一个向量包含所有参数
,然后做乘法就可以 获得所有样本的结果值,如下:

























 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








