Ordinal Regression 年龄估计（CVPR2016）

由于论文时间比较早了，模型也相对较老，因此，本文主要针对文章里面对“ordinal regression”的研究进行整理总结。

论文链接（https://www.cv-foundation.org/openaccess/content_cvpr_2016/papers/Niu_Ordinal_Regression_With_CVPR_2016_paper.pdf）

针对该文章，已经有大量的讨论和分析，但是看完所有相关的分析依然不能理解里面设计的ordinal regression的细节（相关的分析文章链接已在本文末尾给出）。

概述

这一篇cvpr2016的文章，主要是利用多输出CNN(多任务)结合有序回归的思想来解决人脸估计问题，主要的贡献点有两个：

1、用端到端的多任务CNN模型代替之前的SVM处理有序回归问题。

2、提供了一个新的以亚洲人为主的人脸年龄数据集AFAD。

模型

这是文章里面使用到的模型，现在我们来看的话，应该很熟悉了，所以我们不讨论这个模型结构。唯一的重点就是最后使用到的多任务思想。

有序回归（ordinal regression）

进入正题，我们主要讨论里面的有序回归（ordinal regression） 。

介绍年龄估计问题

年龄估计，顾名思义就是要从人脸图片中估计出对象的年龄，一般情况下是一个整数，而不是年龄段（中年，青年）和小数（25.5），这一点符合人的常理，我们在提及自己的年龄时，也不会说“我今年25.5岁”。

常见思路

• Classification

由于年龄估计任务的输出是一个整数，比如0-99岁年龄范围，显然他可以看做一个100分类问题，0-99正好看做100个类。虽然分类的方法是最直接清晰的思路，但是年龄本身有连续性，而分类问题忽略了这种天然的内在联系，因为常规的分类任务，类别间是完全独立的，比如猫狗分类。举个例子：
我们一般用softmax+交叉熵做分类任务的损失，假如有三个类别，分别是猫、狗、鸟，它们分别对应的one-hot编码是[1 0 0]、[ 0 1 0]、[0 0 1]，当前对一张实际类别是猫的图片进行预测，假设预测结果P1为[0.2 0.6 0.2]，P2为[0.2 0.2 0.6]，显然这两次预测结果都是错误，并根据交叉熵计算损失是一样大的，在猫、狗、鸟的三分类问题中，这样来计算损失是合理的。
但是假如我们把这个三分类分别对应0岁，1岁和2岁，这样计算损失就不再合理，因为1岁要比2岁，更加接近于0岁，而1岁和2岁产生的损失却一样大，这就是分类问题应用到年龄估计中的弊端，softmax仅仅强调了类间差异的最大化，却忽略了年龄问题本身的连续性。

• Regression

由于年龄的连续性，年龄估计也可以看做回归问题，但是回归处理假设人的衰老是一个“静态”过程，即不同年龄的人的衰老变化规律一致。

• Ranking

年龄估计过程可以看成是对大量人脸有效信息对进行比较的过程，也就是通过若干组二值分类结果就可以得到相应的年龄估计值，通过寻找当前年龄标签在年龄序列中的相对位置来确定最终的年龄值，从而有效克服了传统的年龄估计方法忽略了人类面部衰老过程中的动态性、模糊性以及个性化的特点。

多个二分类思想

这篇论文不同于传统的分类问题或回归问题处理年龄估计，而是引入了一种Ordinal Regression思想，是在用多个二分类问题实现顺序的年龄回归任务，从而考虑到年龄的连续性特点。

 而二分类的输出就是：是否大于当前的Rank。在本文中，Rank是Ordinal的，如果我们要做1-100岁的年龄估计，那么Rank就有99个，分别对应1-99个年龄，如果第1个任务为1，那么表征预测的人脸年龄大于1，第二个任务为1，预测的人脸年龄大于2，依次类推，直到最后一个任务T=100-1，如果该任务为1，及预测的人脸年龄大于99。
最后的年龄q等于上述所有输出为1的子任务的和，及：

这样定义年龄估计有两个好处：
1.在实际生活中，我们去判断一个人的年龄大于还是小于另一个年龄，要比直接去估计这个年龄更容易，这符合人的主观认知；
2.Ordinal的思想不同于直接分类，利用了年龄本身连续性的特点。

我们还能发现，如果我们预测的任务Task T=100，那么输出将会有2*T，即为200个神经元输出。因为每两个神经元作为一个二分类器（如图所示），两个神经元的取值范围为{0,1}。例如，任务1预测当前年龄是否大于1，大于1则神经元取值为1，否则取值为0，

损失函数

介绍了文章中采用的多个二分类思想处理ordinal regression。接下来介绍怎么设计损失函数。

由于，该方法本质上是在用多个二分类子任务构建Ordinal Regression，所以损失函数采用的是交叉熵，即对每一个子任务的损失函数加权求平均，当我们认为每个要子任务都是同等重要的，那么每个子任务的损失函数为：

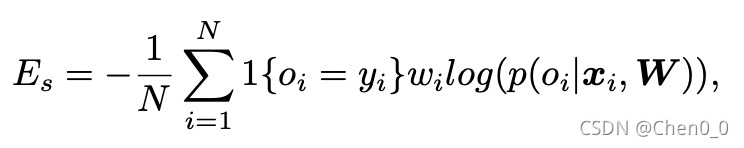
其中yi为标签，oi为输出值， 1{.}表示内部条件成立为1，反之取0。wi为第i个图片的权重。

 因为有T=K-1个子任务，所以所有子任务的损失函数为：

其中 为第t个子任务的权重。

作者还对每个任务基于对应的数据数量设置了权重(λt)，并发现相比于平均分布得到了一些提升：

 

参考：

https://blog.csdn.net/weixin_30496751/article/details/95351551?utm_medium=distribute.pc_relevant.none-task-blog-2~default~baidujs_title~default-0.control&spm=1001.2101.3001.4242

https://zhangxu.blog.csdn.net/article/details/90739483?utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EOPENSEARCH%7Edefault-2.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EOPENSEARCH%7Edefault-2.control