数值作业:二分法求方程的根之C语言实现代码

二分法是求方程近似解的一种简单直观的方法，设函数f(x)在[a,b]上连续，且f(a)*f(b)<0,则表明f(x)在[a,b]上至少有一个零点，这是微积分中的介值定理(不得不吐槽一下大学微分方程老师讲课跟个煞笔一样，反正我是重来没听的）．然后通过二分区间，缩小区间范围，当小到一定的精确度的时候，这个x就是我们所求的近似根了．
个人对算法的分析：１首先输入我们的函数f(x),这里定义为一元三次方程;2,输入求根区间[a,b]和误差控制量eps(在C语言中1e-10代表1*10的负10次方）,用到了fabs()求绝对值的数学库函数．输入步骤完毕．３，判断f(a)*f(b)<0是否为真．为真代表有零点，就可以用二分法不断地缩小空间，得出近似解x了．没有零点就尴尬了，二分法只能计算方程的实根，这里也可以看出二分法的局限性．
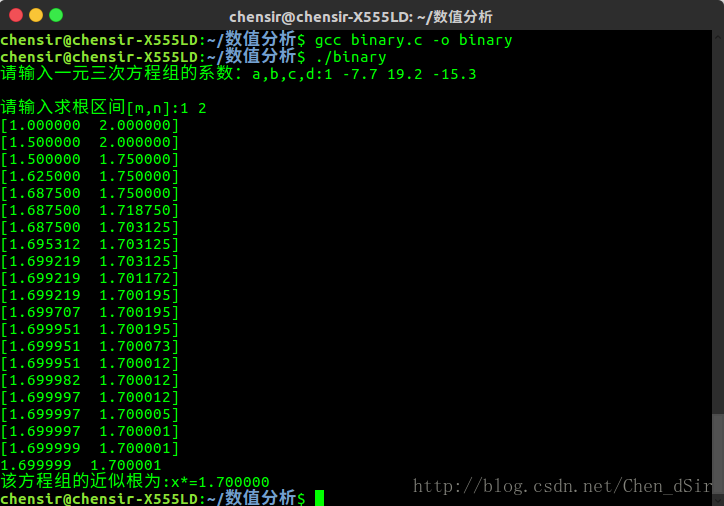
下面给出一个题目：用二分法求f(x)=x*x*x-7.7*x*x+19.2*x-15.3在区间[1,2]之间的根．
下面给出自己写的代码，如下：

/********************************************
    > File Name: Binary.c
    > Author:chendiyang
    > School:WUST_CST_1501班
    > Myblog:www.chendsir.com
    > Mail:1441353519@qq.com 
    > Created Time: 2017年04月18日 星期二 23时55分13秒
 **************************************************/
#include <stdio.h>
#include <math.h>

const double eps = 1e-6; //定义我们计算的精度
double a,b,c,d;        //假定我们输入的函数是一元三次方程组，a*x*x*x+b*x*x+c*x+d=0
double f(double x) //定义我们的函数
{
return a*x*x*x+b*x*x+c*x+d;
}

int main()
{
    double m,n;//求根区间[m,n]
    double i,j,sum;
    printf("请输入一元三次方程组的系数：a,b,c,d:");
    scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
    printf("\n请输入求根区间[m,n]:");
    scanf("%lf%lf",&m,&n);
    if(f(m)*f(n)<0)
    {
        while(fabs(m-n)>eps)
        {
          i=(m+n)/2.0;
          sum=f(i);
          printf("[%lf  %lf]\n",m,n);
          if(fabs(sum)<eps)
           {
               break;
            //printf("\n该方程组的近似根为:x2*=%lf\n",i);
            //return 1;
           }
          else if(f(i)*f(m)<0)
          {
              n=i; //修正区间，将[m,n]换成[m,i],这里的i是中点
          }  
          else if(f(i)*f(n)<0)
          {
              m=i;//修正区间，将[m,n]换成[i,n],这里的i是中点
          }
        }
    }
    else ; //如有其他求根方法，可以加上
    printf("%lf  %lf",m,n);
    j=(m+n)/2;
    printf("\n该方程组的近似根为:x*=%lf\n",j);
}

　　　这道题目就是不停的缩小区间，从而得出近似解，
　　　然而二分法最坑的地方不是它只能计算实根这个问题，最坑的是它当函数f(x)存在几个零点实，它只能计算出一个零点！！这个针对有些算法题目就不好办了．牛顿迭代法和弦切法可以解决它的不足，当然也有它们的局限，every coin has two sides,事物都有两面性，算法也不例外．．．