2017 ACM-ICPC 亚洲区（西安赛区）网络赛 E.Maximum Flow(找规律？)

题意：现在有n个点，编号为0至n-1, 满足i<j的任意两点连一条i^j流量的边，问0到n-1的最大流。 n<=1e18

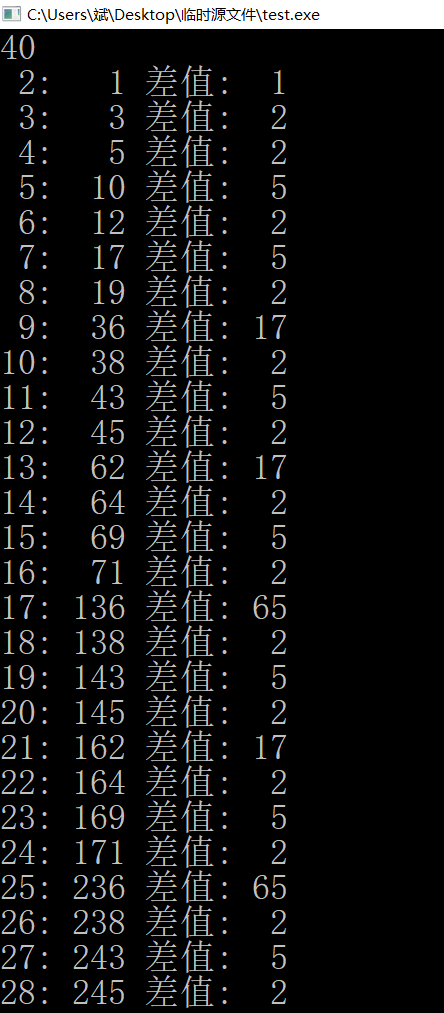
思路：n这么大。。上来就先打个表看下规律吧，结果发现每项与上一项的差值有个规律，相邻2^k的差值为2^(k*2)+1,简单来说就是每个差值（2^(k*2)+1）都从一个位置开始，每隔一定距离出现一次，一个位置同时可能是多个数的话取最大的那个。可以看看表：

知道了这个规律，统计下每种差值在1-n内他出现的次数，最后求和下就行，因为有些位置同时出现多种差值的情况需要取大的那个，所以倒着容斥一下就行，减掉出现过的个数。

代码：

#include<bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
typedef long long ll;
ll fac[63] = {1, 1}, start[63] = {0, 3};
ll ans[100], step[100] = {1, 1};
ll num[100];

void init()
{
    for(int i = 2; i <= 61; i++)
        fac[i] = fac[i-1]*2*2%mod, step[i] = step[i-1]*2;
    start[2] = 5;
    for(int i = 3; i <= 61; i++)
        start[i] = start[i-1]*2-1;
    for(int i = 1; i <= 61; i++)
        start[i] -= step[i];
}

int main(void)
{
    init();
    ll n;
    while(~scanf("%lld", &n))
    {
        memset(ans, 0, sizeof(ans));
        memset(num, 0, sizeof(num));
        ll pre = 0;
        for(int i = 61; i >= 1; i--)
        {
            num[i] = ((max(0LL, n-start[i])/step[i])-pre+mod)%mod;
            ans[i] = num[i]*(fac[i]+1)%mod;
            pre = (pre+num[i])%mod;
        }
        ll res = 1;
        for(int i = 1; i <= 61; i++)
            res = (res+ans[i])%mod;
        printf("%lld\n", res);
    }
    return 0;
}

打表代码：

#include<bits/stdc++.h>
using namespace std;
const int INF = 1e9;
const int maxn = 1e3+5;
const int maxv = 1e6+7;
int head[maxv], cur[maxv], d[maxv], s, t, k, sum;
int n, m, dis[maxn];
struct node
{
    int v, w, next;
}edge[maxv];

void addEdge(int u, int v, int w)
{
    edge[k].v = v;
    edge[k].w = w;
    edge[k].next = head[u];
    head[u] = k++;
    edge[k].v = u;
    edge[k].w = 0;
    edge[k].next = head[v];
    head[v] = k++;

}

int bfs()
{
    memset(d, 0, sizeof(d));
    d[s] = 1;
    queue<int> q;
    q.push(s);
    while(!q.empty())
    {
        int u = q.front();
        if(u == t) return 1;
        q.pop();
        for(int i = head[u]; i != -1; i = edge[i].next)
        {
            int to = edge[i].v, w = edge[i].w;
            if(w && d[to] == 0)
            {
                d[to] = d[u] + 1;
                if(to == t) return 1;
                q.push(to);
            }
        }
    }
    return 0;
}

int dfs(int u, int maxflow)
{
    if(u == t) return maxflow;
    int ret = 0;
    for(int i = cur[u]; i != -1; i = edge[i].next)
    {
        int to = edge[i].v, w = edge[i].w;
        if(w && d[to] == d[u]+1)
        {
            int f = dfs(to, min(maxflow-ret, w));
            edge[i].w -= f;
            edge[i^1].w += f;
            ret += f;
            if(ret == maxflow) return ret;
        }
    }
    return ret;
}

int Dinic()
{
    int ans = 0;
    while(bfs() == 1)
    {
        memcpy(cur, head, sizeof(head));
        ans += dfs(s, INF);
    }
    return ans;
}

int main(void)
{
    int e;
    while(~scanf("%d", &e))
    {
        int pre = 0;
        for(int i = 2; i <= e; i++)
        {
            n = i;
            memset(head, -1, sizeof(head));
            s = 0, t = n-1; k = 0, sum = 0;
            for(int i = 0; i < n; i++)
            {
                for(int j = i + 1; j < n; j++)
                {
                    if(j == n-1) dis[i] = i ^ j, sum += i ^ j;
                    addEdge(i, j, i^j);
                }
            }
            int cur = Dinic();
            printf("%2d: %3d 差值:%3d\n", i, cur, cur-pre);
            pre = cur;
        }
    }
    return 0;
}