加减运算
一、补码的加减运算公式
1、
[X+Y]补 = [X]补 + [Y]补
[X-Y]补 = [X]补 + [-Y]补
说明:
1、使用补码进行加减运算,符号位和数值位一样参加运算。
2、补码的减法可以用加法来实现,任意两数之差的补码等于被减数的补码与**减数相反数的补码(这里有一个求补操作)**之和

那我们来举一些例子来说明一下这个运算:

2、判断补码运算的溢出
我在这里说明一下,我学习这个内容的时候,一直都弄不明白我们的机器检测溢出到底有什么用,然后我后来找到一个说服自己的理由就是:机器检测溢出,如果是下溢,机器就认为这个数是机器零,如果是上溢,机器就没有办法表示这个数,然后可能会发生类似我们程序的一个报错了无法执行,这个时候我们可能要转换数据类型,我也不知道这个想法是对还是不对,所以这里就提出来,错误不要喷。(这个想法的来源是“浮点数的表示范围”)。下面我们切入正题
溢出:当运算结果超出机器数的表示范围时,称为溢出。计算机必须具备检测运算结果是否发生溢出的能力,否则会得到错误的结果。
对于加减运算,常用来判断溢出的方法:
1、确定发生溢出的情况:
正数相加,且结果符号位为1;
负数相加,且结果符号位为0;
正数-负数,且结果符号位为1;
负数-正数,且结果符号位为0;
2、单符号位判溢方法
当最高有效位产生的进位和符号位产生的进位不同时,加减运算发生了溢出。
V=C1⊕Cf,这里当v=1,发生溢出,当v=0,不发生溢出
下面来举一个例子:

这里也说明一下:这里的算数,如果发现比原来的数多了进位,因为机器没有办法存储的宽度是一定的,所以这个进位会被省略掉(大概是这么理解的)
2、双符号位判溢法
X和Y采用双符号位补码参加运算,正数的双符号位为00,负数的双符号位为11;当运算结果的两位符号Sf1 Sf2不同时(01或10),发生溢出。
V= Sf1 ⊕ Sf2= Xf ⊕Yf ⊕Cf⊕ Sf
Sf1 Sf2=01,则正溢出;Sf1 Sf2=10,则负溢出
还是用上面的例子举例子:

========================================
机器数的移位运算
二进制数据(真值)每相对于小数点左移一位,相当于乘以2(也就是题目问的2x);每相对于小数点右移一位,相当于除以2(也就是题目问的x/2)
计算机中的移位运算分为:
1、逻辑移位:将移位的数据视为无符号数据,各数据位在位置上发生了变化,导致无符号数据的数值(无正负)放大或缩小。
2、算术移位:将移位的数据视为带符号数据(机器数)。算术移位的结果,在数值的绝对值上进行放大或缩小,同时,符号位必须要保持不变。
3、循环移位:所有的数据位在自身范围内进行左移或者右移,左移时最高位移入最低位,右移时最低位移入最高位。
1、算术左移:符号位不变,高位移出,低位补0。 为保证补码算术左移时不发生溢出,移位的数据最高有效位必须与符号位相同。 在不发生溢出的前提下,用硬件实现补码的算术左移时,直接将数据最高有效位移入符号位,不会改变机器数的符号。
2、算术右移:符号位不变,低位移出,高位正数补0,负数补1,即高位补符号位。
========================================
移码的加减运算和溢出
X和 Y的移码相加
[X]移+ [Y]移=[X]移+ [Y]补
[X]移- [Y]移=[X]移+ [-Y]补 (所以这里也有一个取补操作,和上面讲的一样)


====================================
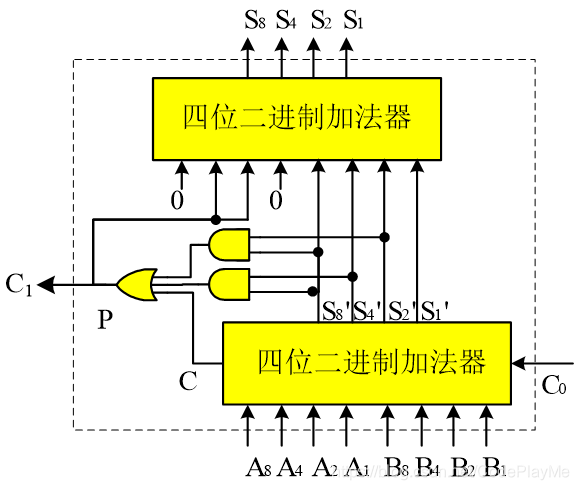
十进制的加法运算




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








