题目描述
数学的王国里,有一些约数国王……约数国王的定义是这样的:一个大于1的整数n,如果它约数的个数比1~n-1的每个整数的约数的个数都要多,那么我们就称它为约数国王。聪明的小明在奥数书上认识了它们,于是产生了一个问题:他想知道L到R之间一共有多少个约数国王?它们分别又是谁?
输入
输入文件只有一行,包含一个l,一个r,表示小明想知道的范围。
输出
只有一行,第一个数h,表示l~r内一共有多少个约数国王,接下来h个从小到大的数(为了防止国王们打架,你需要按顺序输出。),表示约数国王分别是谁。
样例输入
1 100
样例输出
8 2 4 6 12 24 36 48 60
数据范围限制
对于30%的数据,1<=l<=r<=200000。
对于50%的数据,1<=l<=r<=500000。
对于70%的数据,保证最大的约数国王的约数的个数不大于5000。
对于100%的数据,1<=l<=r, 并且保证l,r在64位整型以内,最大的约数国王的约数的个数不大于200000。
吹水时间:
1.“约数国王”的真名是“约数富豪”,是我在《奥数教程》里看到的。我觉得“富豪”太土了,所以改成了“国王”。
2.由于这实在是太坑了,我从有雏形开始,到全部出好,几乎用了半年。
3.鄙人语文实在不算好,所以题目描述比较简陋。
4.感谢XC的大力支持和对题目的修改。
让我们步入正题
不知道机智的你能拿多少分呢?
30
直接暴力就好了,枚举时注意不要枚举所有因数,只需要枚举两个因数中较小的那个因数,就可以得出答案。
注意完全平方数的特殊情况。
时间复杂度 O(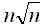
代码(C++):
#include<cstdio>
#include<cmath>
#define fo(i,x,y) for(int i=x;i<=y;i++)
#define p 200000
using namespace std;
long long a[200],l,r,t,f,max;
int main()
{
fo(i,2,p)
{
f=0;
fo(j,1,sqrt(i*1.0)) if(i%j==0)f+=2;
if(floor(sqrt(i*1.0))==sqrt(i*1.0))f--;
if(f>max){max=f;a[++a[0]]=i;}
}
scanf("%lld%lld",&l,&r);
fo(i,1,a[0])if((a[i]>=l)&&(a[i]<=r))t++;printf("%lld",t);
fo(i,1,a[0])if((a[i]>=l)&&(a[i]<=r))printf(" %lld",a[i]);
}50
1.
根据乘法原理,设k=p1^q1*p2^q2*p3^q3…pn^qn(p_i是k的质因数,q_i是p_i对应的指数),则k的约数的个数为(q1+1)(q2+1)(q3+1)…(qn+1)。
让我们举个栗子:
假设有一数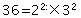
那么其实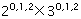
因为可以是0,所以需要把各指数加一,然后乘起来,就是约数的个数了。
那么,通过枚举k的质因数和指数,也可以求出k的约数的个数。注意同样是枚举小于等于根号k的质因数,不要枚举全部。
设p_0表示根号n以内质数的个数,则时间复杂度O(n p_0)
代码(C++):
#include<cstdio>
#include<cmath>
#define fo(i,x,y) for(int i=x;i<=y;i++)
using namespace std;
const int max=500000,po=sqrt(max*1.0);
bool bz[po+1];
int f[max+1],p[169],a[200],mx,l,r,t;
int main()
{
fo(i,2,po)
{
if (!bz[i]) p[++p[0]]=i;
fo(j,1,p[0])
{
if(max/p[j]<i) break;
bz[i*p[j]]=1;
if (i%p[j]==0) break;
}
}
fo(i,1,max)
{
f[i]=1; int k=i;
fo(j,1,p[0])
{
if (p[j]>sqrt(i*1.0)) break;
if (k==1) break;
int a=0;
while (k%p[j]==0)
{
a++;k/=p[j];
}
f[i]*=a+1;
}
if (k>1) f[i]*=2;
if(f[i]>mx){mx=f[i];a[++a[0]]=i;}
}
scanf("%lld%lld",&l,&r);
fo(i,1,a[0])if((a[i]>=l)&&(a[i]<=r))t++;printf("%lld",t);
fo(i,1,a[0])if((a[i]>=l)&&(a[i]<=r))printf(" %lld",a[i]);
}
2.
线性筛法求约数的个数,详细请参考:
http://blog.csdn.net/cold_chair/article/details/51525699
70
设c(y)表示有y个因数的最小的正整数,
那么当c(y)< c(y+1),c(y+2),c(y+3),…,c(y+k)的时候,c(y)就是一个约数国王。
至于y+k,我们假想它很大就行了。
那么问题转换成了如何求c(y),此时可以想到动态规划。
设f(x)(y)表示有x个不同的质因数,因数的个数为y的最小的正整数,那么很容易想到这x个质数肯定是最小的连续的x个质数,即2,3,5,7,11…
根据之前的“(q1+1)(q2+1)(q3+1)…(qn+1)”,很容易得出状态转移方程f(x)(y)=f(x-1)(y/(k+1))*p_x^k (1<=k<=y)(k+1|y)。
p_x指的是第x大的质数。
x最大是log2 y,因为每增加一个不同的质因子,约数的个数至少要乘以2(即对应的指数为一)。
时间复杂度O(n n log2n)
实际上会小得很多,如果常数比较优美,甚至可以直接卡过。如果卡不过,打表也行了。
代码(pascal):
const
am=5000;
up=100000;
an=trunc(ln(am)/ln(2));
man=9223372036854775807;
var
op,max,l,r:int64;
i,j,k,q,w,t:longint;
a:array[0..am] of int64;
bz:array[2..up] of boolean;
p:array[0..10000] of int64;
f:array[1..an,1..am] of int64;
m:array[2..am] of int64;
function min(x,y:int64):int64;
begin
if x<y then exit(x) else exit(y);
end;
begin
for i:=2 to up do
begin
if not bz[i] then
begin
inc(p[0]);
p[p[0]]:=i;
if p[0]=an then break;
end;
for j:=1 to p[0] do
begin
if i*p[j]>up then break;
bz[i*p[j]]:=true;
if i mod p[j]=0 then break;
end;
end;
for i:=1 to an do
for j:=1 to am do
f[i,j]:=man;
f[1,2]:=p[1];
for j:=3 to 62 do
f[1,j]:=f[1,j-1]*p[1];
for i:=2 to an do
begin
for j:=1<<i to am do
begin
op:=1;
for k:=1 to j>>1-1 do
begin
if p[i]>man/op then break;
op:=op*p[i];
if j mod (k+1)>0 then continue;
if op>man/f[i-1,j div (k+1)] then continue;
if f[i-1][j div(k+1)]*op<f[i][j] then
f[i][j]:=f[i-1][j div (k+1)]*op;
end;
end;
end;
for j:=2 to am do
begin
m[j]:=man;
for i:=1 to an do
m[j]:=min(m[j],f[i,j]);
end;
max:=man;
for i:=am downto 2 do
begin
m[i]:=man;
for j:=1 to an do
m[i]:=min(m[i],f[j,i]);
end;
for i:=am downto 2 do
begin
if m[i]<max then
begin
inc(a[0]); a[a[0]]:=m[i]; max:=m[i];
end;
end;
read(l,r);
q:=0;
for j:=1 to a[0] do
if (a[j]>=l)and(a[j]<=r) then inc(q);
write(q);
for j:=a[0] downto 1 do
if (a[j]>=l)and(a[j]<=r) then write(' ',a[j]);
writeln;
end.
100:
其实70分和100分是一样的,100分是70分的优化。
方程里有一个条件(k+1| y),我们可以想办法把它弄掉:
如果想要求f(x)(y),需要穷举所有的f(x-1)(…),十分的不值,因为很多数明显都不是y的因数。其实当我们求出一个f(x)(y)时,就可以用它去维护f(x+1)(y的倍数),这样,
求一个f(x)(y)的时间就是y的因数的个数,平均下来是log2y。
注意求出的f(x)(y) 有可能会超过64位整形,如果超过了,就给它个无穷大,不理它就行了,因为题目只要我们求出64位整形以内的约数国王。
这样就可以AC了,时间复杂度O(n log2 n log2n)。实际上要小得很多,原因前面已经说明。
优化:
1.
若一个数k=p1^q1*p2^q2*p3^q3…pn^qn,由于p是有序的,所以当p,q(不按顺序,只考虑数字)都相同时,p,q成不上升序,k才能最小。
那么我们可以记录一个min(x)(y),表示f(x)(y)中q_x的值,只有当k<=min(x)(y)时,才去更新f(x)(y*(k+1)),这么做,又可以去掉许多不必要的计算。
2.
空间复杂度是O(n log n),不算很大。但是我们打个滚动数组会更好,时间也会小一些。
最终程序(C++):
#include<cstdio>
#include<cmath>
#define fo(i,x,y) for(int i=x;i<=y;i++)
const int am=170000,an=17,up=100;
int min[am+1],min1[am+1];
bool bz[up+1];
long long a[300],p[up+1],f[am+1],f1[am+1],m[am+1];
long long max=9223372036854775807LL;
int main()
{
fo(i,2,up)
{
if (!bz[i]) p[++p[0]]=i;
fo(j,1,p[0])
{
if (up/p[j]<i) break;
bz[i*p[j]]=1;
if (i%p[j]==0) break;
}
}
f[1]=1; fo(i,2,62) {f[i]=f[i-1]*2;min[i]=i-1;}
fo(i,63,am)f[i]=max;
fo(i,2,am) m[i]=max;
fo(i,1,16)
if (i%2)
{
fo(j,1<<(i+1),am) f1[j]=max;
fo(j,1<<i,am)
{
if (f[j]==max) continue;
if (f[j]<m[j]) m[j]=f[j];
double y=log(max/f[j])/log(p[i+1]);
if(am/(j+1)-1<y) y=am/(j+1)-1;
if(min[j]<y) y=min[j];
long long op=1;
fo(k,1,y)
{
op*=p[i+1];
if(f[j]*op<f1[j*k+j])
{
f1[j*k+j]=f[j]*op;
min1[j*k+j]=k;
}
}
}
} else
{
fo(j,1<<(i+1),am) f[j]=max;
fo(j,1<<i,am)
{
if (f1[j]==max) continue;
if (f1[j]<m[j]) m[j]=f1[j];
double y=log(max/f1[j])/log(p[i+1]);
if(am/(j+1)-1<y) y=am/(j+1)-1;
if(min1[j]<y) y=min1[j];
long long op=1;
fo(k,1,y)
{
op*=p[i+1];
if(f1[j]*op<f[j*k+j])
{
f[j*k+j]=f1[j]*op;
min[j*k+j]=k;
}
}
}
}
fo(i,1<<17,am)if(f[i]<m[i])m[i]=f[i];
long long x=max;
for(int i=am;i>1;i--)
if(m[i]<x)
{
a[++a[0]]=m[i];
x=m[i];
}
long long l,r;
scanf("%lld %lld",&l,&r);
int y=0;
fo(i,1,a[0]) if ((a[i]>=l)&&(a[i]<=r)) y++;
printf("%d",y);
for(int i=a[0];i>=1;i--)
if ((a[i]>=l)&&(a[i]<=r))
{
printf(" %lld",a[i]);
}
}





















 1450
1450

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








