打印一个n行的杨辉三角形两种方法（详细解释，细到数学公式推导）

第一种是循环语句嵌套

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int main() {
    int n, coef = 1;

    printf("请输入一个整数n：");
    scanf("%d", &n);

    for (int i = 0; i < n; i++) 
    {
        // 打印每行前面的空格，使三角形居中显示
        for (int space = 1; space <= n - i; space++)
        {
            printf(" ");
        }

        for (int j = 0; j <= i; j++) 
        {
            if (j == 0 || i == 0) 
            {
                coef = 1;
            }
            else 
            {
                coef = coef * (i - j + 1) / j;
            }
            printf("%4d", coef);
        }
        printf("\n");
    }

    return 0;
}

首先这是完整的代码接下来让我来解释为什么这样写

这是一个杨辉三角，对于杨辉三角，先要知道几条性质，我们将最顶上那个1的编为（0，0）（行，列）

1.杨辉三角行与列数量相同

2.有且仅有两种情况该项为1，第一种当行与列相同的时候，第二种当列为0的时候

3.杨辉三角符合二项式定理展开系数规律，及其行列就对应求和公式。

4.杨辉三角某一项的值是左边一项乘以(m-n+1)/n，推导过程如下

for (int i = 0; i < n; i++) 
    {}

 最外层的for是为了生成行，这里的n是我们先前输入的总行数

for (int space = 1; space <= n - i; space++)
        {
            printf(" ");
        }

这一步是为了让杨辉三角居中，至于space为什么要小于等于n -  i我们画个图就知道了，假设生成4行

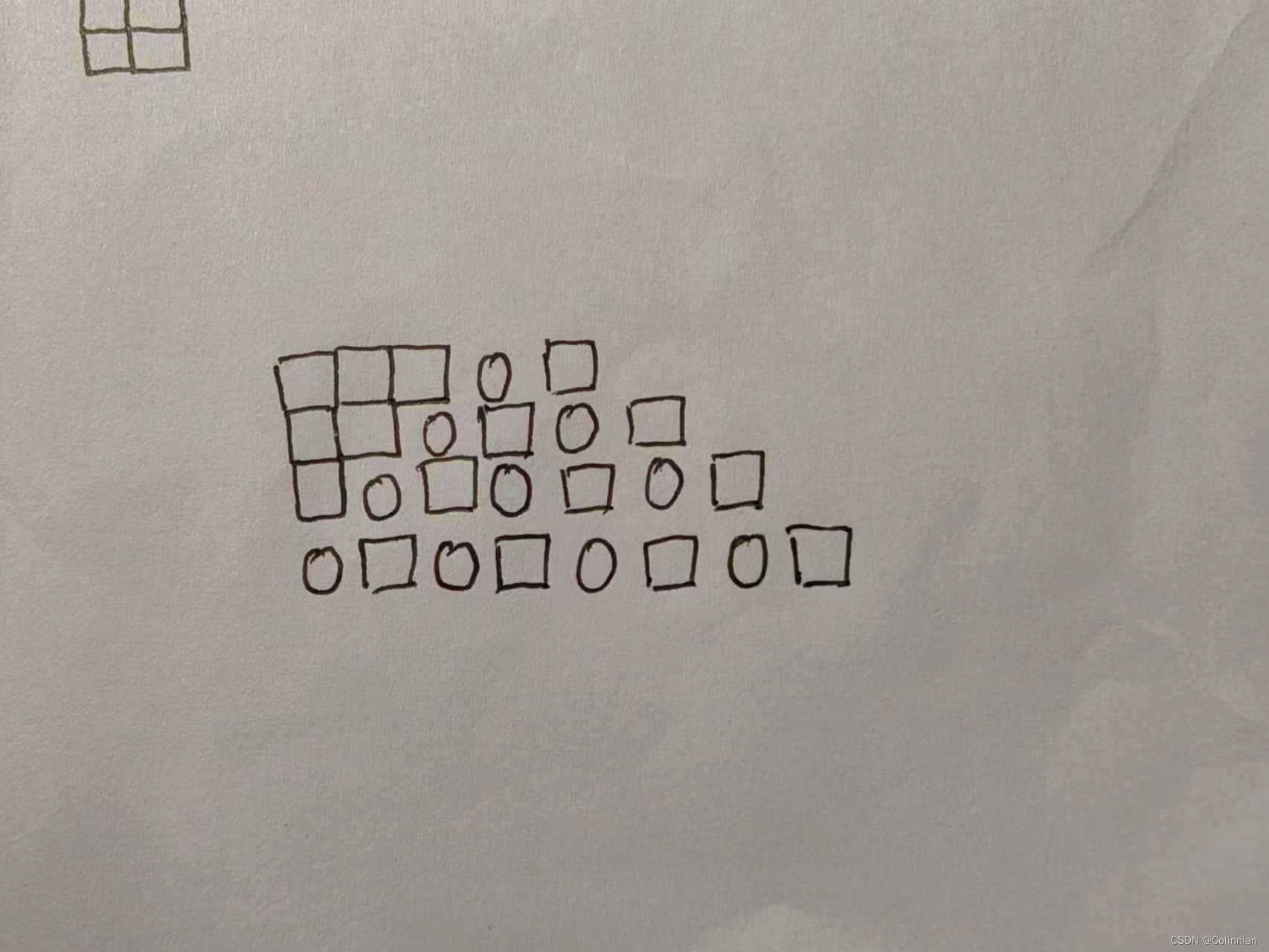
 圆圈代表数字，方框代表空格，最后一行4-4刚好等于0，前面便不会有空格。

for (int j = 0; j <= i; j++) 
        {
            if (j == 0 || i == 0) 
            {
                coef = 1;
            }
            else 
            {
                coef = coef * (i - j + 1) / j;
            }
            printf("%4d", coef);
        }
        printf("\n");

这一步我们首先用循环语句生成了列，对应性质1，我们要让列小于等于行，所以j<=i。

然后在嵌套一个·if语句，if的条件对应性质2，上面有写，这里是把1打印出来，else则对应其它情况，这里则是对应性质4，我们仅仅是把公式罗列上去了，

下面%4d取决于你要打印的行数，如果某一行的某一项超过4个字符了，则要改成%5d。

到此，只要依照循环，按顺序一个一个打印出来就行了。

第二种方法是函数递归

首先要补充一条性质，项（m，n）是由项（m-1,n-1）+(n-1,m)而成

下面是完整的代码

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
// 计算杨辉三角形的值
int calculateValue(int row, int col) {
    if (col == 0 || col == row) {
        return 1;
    }
    else {
        return calculateValue(row - 1, col - 1) + calculateValue(row - 1, col);
    }
}

// 打印n行的杨辉三角形
void printPascalTriangle(int n) {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= i; j++) {
            printf("%d ", calculateValue(i, j));
        }
        printf("\n");
    }
}

int main() {
    int n;

    printf("请输入一个整数 n: ");
    scanf("%d", &n);

    if (n < 0) {
        printf("请输入一个非负整数。\n");
    }
    else {
        printPascalTriangle(n);
    }

    return 0;
}

主函数的if和else想必不用多讲，从else进入到第一个函数，第一个函数

void printPascalTriangle(int n)是为了生成行和列，和第一种方法里的for循环嵌套一个道理，

然后每生成一个行和列便把（i，j）传给第二个函数

int calculateValue(int row, int col) {
    if (col == 0 || col == row) {
        return 1;
    }
    else {
        return calculateValue(row - 1, col - 1) + calculateValue(row - 1, col);
    }
}

第二个函数的if条件就是我们所讲的性质1，行列相同，或列为0是，该项为1，紧接着进入else，便是我们补充的性质（首先要补充一条性质，项（m，n）是由项（m-1,n-1）+(n-1,m)而成）把他拆成两项再去运算，直到计算到第一项为止，然后在加和回来，最后就可以得到我们的结果了，不过递归只适用于次数较少的运算。所以我认为还是第一种方法比较好。

第一个函数这里忘了写让它居中的代码了，这里补充一下

void printPascalTriangle(int n) {
    for (int i = 0; i < n; i++) 
    {
        for (int space = 1; space <= n - i; space++)
        {
            printf(" ");
        }
        for (int j = 0; j <= i; j++) {
            printf("%d ", calculateValue(i, j));
        }
        printf("\n");
    }
}

最后让我们运行一下看看结果吧！！

 第一次写文章，完结撒花！！