复分析——第3章——亚纯函数和对数(E.M. Stein & R. Shakarchi)-CSDN博客

本文链接：https://blog.csdn.net/ComputerInBook/article/details/139702558

第3章 亚纯函数和对数

(Meromorphic Functions and the Logarithm)

One knows that the differential calculus, which has

contributed so much to the progress of analysis, is

founded on the consideration of differential coefficients,

that is derivatives of functions. When one attributes

an infinitesimal increase ε to the variable x, the function

f (x) of this variable undergoes in general an infinitesimal

increase of which the first term is proportional

to ε , and the finite coefficient of ε of this increase

is what is called its differential coefficient... If

considering the values of x where f (x) becomes infinite,

we add to one of these values designated by $x_{1}$ ,

the infinitesimal ε, and then develop $f(x_{1}+\epsilon)$

in increasing power of the same quantity, the first terms

of this development contain negative powers of ε; one

of these will be the product of 1/ε with a finite coefficient,

which we will call the residue of the function

f (x), relative to the particular value $x_{1}$ of the variable

x. Residues of this kind present themselves naturally

in several branches of algebraic and infinitesimal analysis.

Their consideration furnish methods that can be

simply used, that apply to a large number of diverse

questions, and that give new formulae that would seem

to be of interest to mathematicians...

(人们知道，对分析的进步贡献如此之大的微积分，它是建立在对微分系数(即，函数的导数)的考量之上的，当有人把一个无穷小递增量 ε 归因于变量x的时候，该变量的函数 f (x)通常会经历其第一项与 ε 成比例的无穷小的增长，这个递增的 ε 的有限系数就是所谓的微分系数……，若考虑在其中 f (x)变成无限时的x的值，我们添加由 $x_{1}$ 指定的这些值之一，无穷小量 ε ，然后按递增的同一个量的幂展开(develop) $f(x_{1}+\epsilon)$ ，展开式(development)中的第一项包含 ε 的负幂；展式项之一将是1/ε 与一个有限系数之积，我们称这个有限系数为函数 f (x) 相对于变量 x 的这个特定值 $x_{1}$ 的留数(residue)。这种类型的留数在代数和无穷小分析的几个分支中自然地呈现了出来。对它们的考量诞生了可以简单使用的方法，这些方法适用于大量不同的问题，并因此给出了数学家似乎感兴趣的新公式......)

---------------------------------------------------------------------------A. L. Cauchy, 1826

该理论中有一个普遍原理，已经隐含在Riemann的著作中，该原理指出，解析函数在本质上以其奇点(singularities)为特征。也就是说，全局解析函数由它们的零点“有效地”确定，亚纯函数(meromorphic functions)由它们的零点和极点(poles)确定。虽然这些论断不能被表述为精确的一般定理，但仍然存在应用该原理的重要实例。

我们首先考虑奇点，特别是全纯函数可以有不同类型的点之奇点(“孤立(isolated)”奇点)。按照递增的严重程度(severity)的顺序，这些奇点类型是：

$\bullet$ 可除奇点(removable singularities)；

$\bullet$ 极点(poles)；

$\bullet$ 本征奇点(essential singularities)。

第一种类型的奇点是“无害”的，因为函数实际上可以在其可除奇点处扩展为全纯函数(因此得名可除奇点)。在第三种类型的奇点附近，该函数的振荡和增长速度可能比任何幂都快，并且要完全理解其行为并非易事。对于第二种类型的奇点，对其分析更直接，并且与留数积分相关，其产生如下所述。

我们记得，根据Cauchy定理，在一个含于闭合曲线γ及其内部的开集中的全纯函数 f 满足

$\displaystyle \int_{\gamma}f(z)dz=0$ 。

所出现的问题是：若 f 在曲线的内部有一个极点会发生什么？为了回答这个问题，考虑例子 f (z) = 1/z 并回顾事实——若C 是一个以0为圆心的(正向)圆，则

$\displaystyle \int_{C}\frac{1}{z}dz=2\pi{i}$ 。

这被证明是留数积分中的关键要素(ingredient)。

当我们考虑具有奇点的全纯函数的不定积分时，一个新的方面出现了。例如，基础函数f (z) = 1/z 表明，最终的“函数”(在这种情况下是对数)可能不是单值的，理解这种现象对于许多学科来说是非常重要的。探索这种多值性(multi-valuedness)实际上导致了“论证原理(argument principle)”。 我们可以利用这个原理来计算合适曲线内全纯函数的零点数量。作为这个结论的一个简单推论，我们获得了全纯函数的一个重要的几何属性：它们是开放映射(open mappings)。从这点出发，(证明)全纯函数的另一个重要特征(最大值原理)就很容易了。

为了转向对数本身，并掌握其多值性的准确特征，我们引入了曲线同伦(homotopy)和简单连通域(simply connected domain)的概念。正是在后一种类型的开集上，可以定义对数的单值分支。

1. 零和极点(Zeros and poles)

根据定义，一个函数 f 的奇点(point singularity)是这样一个复数点(不妨记为 $z_{0}$ ) —— $z_{0}$ 使得函数 f 在 $z_{0}$ 点的邻域内有定义但在 $z_{0}$ 点本身处无定义。我们也将称这样的奇点为孤立奇点(isolated singularities)。例如，若函数使用f (z) = z仅被定义于穿孔平面(punctured plane)上，则圆点即是一个奇点。当然，在这种情况下，函数实际上是可以被定义的( 通过置 f (0) = 0 ), 因此，最终的扩展是连续且事实上是复可积函数(entire)。(这样的奇点则称为可移除奇点(removable singularities))(译注：后面都简称其为“可除奇点”)。更有趣情况的是函数 g (z) = 1/z 定义于穿孔平面的这种情况。现在，可以明确的是，函数g不能定义为一个连续函数，更不用说在0 处定义为一个全纯函数了。事实上，随着 z趋近于0，函数增长到无穷大，我们将称原点是一个极型奇点(pole singularity)。最后，函数 $h(z)=e^{1/z}$ 定义于穿孔平面的这种情况表明，可除奇点和极点并不能呈现出事情的全部特征。事实上，在正实轴上，函数h(z) 随着 z 趋近于0而增长到无穷大，而在负实轴上，函数h (z) 随着 z 趋近于0而趋近于 0 。最后，随着z在虚轴上趋近于原点，h迅速摆动，但仍保持有界。

由于奇点经常因分数的分母消失而出现，因此我们从全纯函数的零点开始进行局部研究。

对于全纯函数 f ，若 $f (z_{0}) = 0$ , 则称 $z_{0}$ 是其零点(zero)。特别是，解析延拓(analytic continuation)表明，非平凡(non-trivial)全纯函数的零点是孤立的。换句话说，若 f 在Ω中是全纯的，并且对于某个 $z_{0} \in \Omega$ ，有 $f (z_{0}) = 0$ ，则存在 $z_{0}$ 的一个开邻域 U ，使得对于任意 $z \in U - \{z_{0}\}$ ， $f (z ) \neq 0$ (除非 f (z ) 恒为0 ) 。我们从接近零的全纯函数的局部描述开始。

定理 1.1 假设 f 在一个连续开集 Ω 中是全纯函数，且在一点 $z_{0} \in \Omega$ 处有一个零点，并在Ω中恒不消没。则存在 $z_{0}$ 的一个邻域 U ⊂ Ω ，在U上存在一个非消没的全纯函数 g ，以及存在一个唯一的正整数 n，使得对于任意 z ∈ U ，有

$f (z ) = (z-z_0)^{n}g(z )$ 。

证明：

因为Ω是连通的且 f 不恒为 0,我们推断出 f 在 $z_{0}$ 的一个邻域内不恒为零。在以 $z_{0}$ 为圆心的一个小圆盘内，f 有幂级数展式

$\displaystyle f (z ) = \sum_{k=0}^{\infty}a_{k}(z-z_{0})^{k}$ 。

因为 f 在 $z_{0}$ 的附近不恒为 0 ,则存在一个使得 $a_{n} \neq 0$ 的最小整数n 。则，我们可以写为

$f (z ) = (z-z_{0})^{n}[a_{n} + a_{n+1}(z-z_{0}) + ...] = (z-z_{0})^{n}g(z )$ 。

其中，g使用方括号中的级数定义，因此是全纯的，且对于接近 $z_{0}$ 的任意 z ，函数处处不消没(因为 $a_{n} \neq 0$ )。为了证明整数 n 的唯一性，假设我们也可以写成

$f (z ) = (z-z_{0})^{n}g(z ) = (z-z_{0})^{m}h(z )$ ，

其中，h(z ) ≠ 0 。若 m > n ，则我们可以使用 $(z-z_0)^{n}$ 除以表达式，从而看到

$g(z ) = (z-z_{0})^{m-n}h(z )$ ,

并令 $z \rightarrow z_{0}$ 并产生了 $g(z_{0} ) = 0$ , 则产生了矛盾。若 m < n ，则按类似的论证便给出 $h(z_{0} ) = 0$ ，这也是一个矛盾。因此，我们推断出 m = n 且 h = g ，定理得证。

在以上定理的情况下，我们称 f 在 $z_{0}$ 点具有n 阶 0 (zero of order n)(或重数n (multiplicity n))。若零的阶数是1，则我们称其是简单的(simple)(零)。我们观察到，从量化上讲，阶描述了函数消没的速率。

前面定理的重要性来自于事实——现在，我们可以准确地表述函数 1/f 在 $z_{0}$ 点据有的奇点类型。

为止目的，现在方便定义 $z_{0}$ 的一个可删除邻域(a deleted neighborhood)为一个以 $z_{0}$ 为圆心的开圆盘( $z_{0}$ 前添加减号)，即，对于某个 r > 0 , 集合成为

$\{ z: 0 < |z - z_{0} |< r \}$ 。

对于函数 f , 若函数 1/f (在 $z_{0}$ 点定义为0 )在 $z_{0}$ 的整个邻域内都是全纯函数，则我们称定义于 $z_{0}$ 的一个可删除邻域中的一个函数 f 在 $z_{0}$ 点有一个极点(pole)。

定理 1.2 若 f 在 $z_{0}\in \Omega$ 处有一个极点，则在那一个点的邻域内，存在一个非消没全纯函数h和一个唯一的正整数 n 使得

$f (z ) = (z-z_{0})^{-n}h(z )$ 。

证明：

根据前面的定理，我们有 $1/ f (z ) = (z-z_{0})^{n}g(z )$ ，其中，g 是全纯函数并且在 $z_{0}$ 的一个邻域内是非消没的。所以，用 h (z ) = 1/ g (z )便推导出了结论。

称整数n为极点的阶(或重数),并用以描述函数在 z0 点附近增长的速率。若极点的阶为1，则我们称其为简单的(极点)(或称“一阶极点”)。

下一个定理应该让人想起(reminiscent)幂级数展式，只不过现在我们允许负阶项来解释极点的存在

定理 1.3 若 f 在 $z_{0}$ 点有一个 n 阶极点，则

(1) $\displaystyle f (z ) = \frac{a_{-n}}{(z-z_{0})^{n}} + \frac{a_{-n+1}}{(z-z_{0})^{n-1}} + ... + \frac{a_{-1}}{z-z_{0}} + G(z )$ ，

其中，G 在 $z_{0}$ 的一个邻域内是全纯函数。

证明：

证明来自前面定理中的乘法表述。事实上，函数 h 有一个幂级数展式

$h (z ) = A_{0} + A_{1}(z - z_{0}) + ...$ ，

因此，

$\begin{array}{rlc} f (z ) &\displaystyle= (z-z_{0})^{-n} (A_{0} + A_{1}(z - z_{0}) + ... ) \\ \\ &\displaystyle= \frac{a_{-n}}{(z-z_{0})^{n}} + \frac{a_{-n+1}}{(z-z_{0})^{n-1}} + ... + \frac{a_{-1}}{z-z_{0}} + G(z ) \end{array}$ 。

称和式

$\displaystyle \frac{a_{-n}}{(z-z_{0})^{n}} + \frac{a_{-n+1}}{(z-z_{0})^{n-1}} + ... + \frac{a_{-1}}{z-z_{0}}$

为 f 在极点 $z_{0}$ 的主要部分(principal part), 系数 $a_{-1}$ 是 f 在这个极点的留数(residue)。

我们记为 $res_{z_{0}} f = a_{-1}$ 。留数的重要性来自于这样一个事实：主要部分中的所有其他项，即那些阶数严格大于 1 的项，都在 $z_{0}$ 的一个删除邻域中具有原函数。因此，若用 P(z)表示上述主要部分，用C表示任意圆心位于 $z_{0}$ 点的圆，我们得到

$\displaystyle \frac{1}{2\pi{i}} = \int_{C} P(z)dz = a_{-1}$ 。

在关于留数公式的章节我们还将回到这个重点。

正如我们将会看到，在很多情况下，积分的计算归结为留数的计算。在 f 在 $z_{0}$ 点有简单极点的这种情况下，可以明确

$\displaystyle res_{z_{0}} f = \lim_{z \rightarrow z_{0}}(z-z_{0})f(z)$ 。

若极点是更高阶的，类似的公式也成立，也涉及微分和取极限。

定理 1.4 若 f 在 $z_{0}$ 点有一个 n 阶极点，则

$\displaystyle res_{z_{0}} f = \lim_{z \rightarrow z_{0}}\frac{1}{(n-1)!}\left ( \frac{d}{dz}\right )^{n-1} (z-z_{0})^{n}f(z)$ 。

这个定理是公式(1)的直接应用的结果，意味着

$\displaystyle (z-z_{0})^{n} f(z) = a_{-n} + a_{-n+1}(z - z_{0}) + ... + a_{-1} (z-z_{0})^{n-1} + G(z )(z-z_{0})^{n}$ 。

2. 留数公式(The residue formula)

我们现在讨论著名的留数公式。我们的方法遵循上一章中对Cauchy定理的讨论：我们首先考虑圆及其内部圆盘的情况，然后解释对可构周线(toy contours)及其内部的一般化(generalizations)。

定理 2.1 假设 f 在包含圆 C 及其内部(除去在 C 内的一个奇点 $z_{0}$ 处)的一个开集上是全纯的。则

$\displaystyle \int_{C} f(z)dz = 2\pi{i}\:\mathrm{res}_{z_{0}} f$ 。

证明：

再一次地，我们可以选择避开极点的锁眼周线，并令窄带(corridor)趋于0，从而看到

$\displaystyle \int_{C} f(z)dz = \int_{C_\epsilon} f(z)dz$ ，

其中， $C_{\epsilon}$ 是以极点 $z_{0}$ 为圆心以 ε 为半径的小圆。

现在，我们观察到

$\displaystyle \frac{1}{2\pi{i}}\int_{C_{\epsilon}}\frac{a_{-1}}{z-z_{0}}dz = a_{-1}$

是Cauchy积分公式(前一章定理 4.1) 应用于常量函数 $f = a_{-1}$ 的直接结果。类似地，当 k > 1 时,通过使用相应的求导公民(也是前一章推论 4.2)，得到

$\displaystyle \frac{1}{2\pi{i}}\int_{C_{\epsilon}}\frac{a_{-1}}{(z-z_{0})^{k}}dz = 0$ 。

但我们知道，在 $z_{0}$ 的一个邻域内，我们可以写成

$\displaystyle f (z) = \frac{a_{-n}}{(z-z_{0})^{n}} + \frac{a_{-n+1}}{(z-z_{0})^{n-1}} + ... + \frac{a_{-1}}{z-z_{0}} + G(z )$ ，

其中，G(z )是全纯的。根据 Cauchy 定理，我们还知道 $\int_{C_{\epsilon}}G(z)dz=0$ , 因此， $\int_{C_{\epsilon}}f(z)dz=a_{-1}$ 。这就意味着预期的结果。

这个定理可以推广到在圆中有有限多个极点的情况和可构周线的情况。

推论 2.2 假设 f 在包含圆C及其内部(除去在C内的奇点 $z_{1},...,z_{N}$ 处)的一个开集上是全纯的。则

$\displaystyle \int_{C} f(z)dz = 2\pi{i} \sum_{k=1}^{N}res_{z_{k}}f$ 。

为了证明，考虑一个多个锁眼周线，其中有一个避开每个极点的环。令窄带(corridor)的宽度趋于零。在极限中，大圆上的积分等于适用定理 2.1 的小圆上的积分之和。

推论 2.3 假设 f 在包含一条可构周线 γ 及其内部(除去在C 内的奇点 $z_{1},...,z_{N}$ 处)的一个开集上是全纯的。则

$\displaystyle \int_{\gamma} f(z)dz = 2\pi{i} \sum_{k=1}^{N}res_{z_{k}}f$ 。

在上述公式中，我们取的 γ具有正方向。证明过程包括选择适合给定可构周线的锁眼，这样，正如我们之前所看到的，我们可以将情况简化为在适用于定理 2.1 的极点周围的小圆上进行积分。

称恒等式 $\int_{\gamma} f(z)dz = 2\pi{i} \sum_{k=1}^{N}res_{z_{k}}f$ 为留数公式(residue formula)。

2.1 例子

留数计算提供了一种计算各种积分的强大技巧。在下面我们给出的例子中，我们计算形如

$\int_{-\infty}^{\infty}f(x)dx$

的3种广义(improper)Riemann积分。主要思想是将 f 延拓到复平面，则选择一个可构周线族 γR 使得

$\displaystyle \lim_{R \rightarrow \infty}\int_{\gamma{R}}f(z)dz = \int_{-\infty}^{\infty}f(x)dx$ 。

根据计算 f 在其极点处留数的方法，我们容易求得 $\int_{\gamma {R}}f(z)dz$ 。挑战点在于选择合适周线族γR 以使得以上极限成立。通常，这种选择由 f 的衰退(decay)行为触发。

例子1：

首先，我们根据周线积分证明

(2) $\displaystyle \int_{-\infty}^{\infty}\frac{dx}{1+x^{2}}=\pi$ 。

注意，若我们作变量替换 $x \mapsto x/y$ ，得到

$\displaystyle \frac{1}{\pi}\int_{-\infty}^{\infty}\frac{ydx}{y^{2}+x^{2}} =\int_{-\infty}^{\infty}\mathcal{P}_y (x) dx$ 。

换句话说，公式(2)指的是，对于每一个y,Poisson核的积分等于1。这一点在第一册书的第5章的引理2.5中非常容易地得以证明，因为 $1/(1+x^{2})$ 是函数 arctan(x)的导数。因此，我们提供了一种导向(2)的另一种证明的留数计算公式。

考虑函数

$\displaystyle f(z)=\frac{1}{1+z^{2}}$ ，

其在复平面上除了在简单极点 i 和 –i 处，函数是全纯函数。此外，我们选择图1所示的周线 γR 。

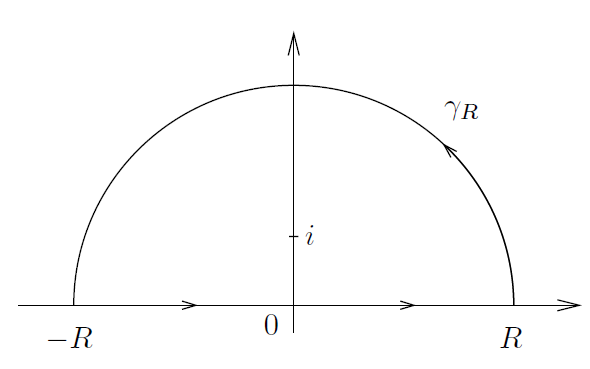
---------------------------------------------图1：例1中的周线 γR ---------------------------------------------------

这个周线由位于实轴上的线段[-R,R]和位于上半平面上且圆心位于圆点的一个大的半圆周构成。

由于我们可以写成

$\displaystyle f(z)=\frac{1}{(z+i)(z-i)}$ ,

我们可以看到，f 在 i 点的留数是1/(2i)。因此，若R足够大，我们就有

$\displaystyle \int_{\gamma{R}} f(z)dz = \frac{2\pi{i}}{2{i}} = \pi$ 。

若我们用 $C_{R}^{+}$ 表示半径为 R 的大半圆，我们会看到

$\displaystyle \left | \int_{C_{R}^{+}}f(z)dz \right | \leq \pi{R}\frac{B}{R^{2}} \leq \frac{M}{R}$ ，

其中，当 $z \in C_{R}^{+}$ 且 R 是大值的时候，我们使用了 $| f (z)| \leq {B}/{|z|^{2}}$ 这个事实。因此，这个积分随着 $R \rightarrow \infty$ 而趋近于 0 。故而，在极限表达式中，我们求得

$\displaystyle \int_{-\infty}^{\infty}f(x)dx=\pi$ ,

正如预期。我们注意到(remark)，在这个例子中，我们选择上半平面的半圆并没有什么特别之处。如果使用下半平面中的半圆，并使用另一个极点和合适的留数，则可以得到相同的结果。

例子2：

以下是将在第6章中扮演重要作用的积分：

$\displaystyle \int_{-\infty}^{\infty}\frac{e^{ax}}{1+e^{x}}dx=\frac{\pi}{\sin(\pi{a})}(0<a<1)$ 。

为了证明这个公式，我们令 $f (z) = e^{az}/(1+e^{z})$ ，并考虑位于上半平面且一边位于实轴上,而另一个平行边位于直线 Im(z) = 2π 上的矩形周线, 如图2所示。

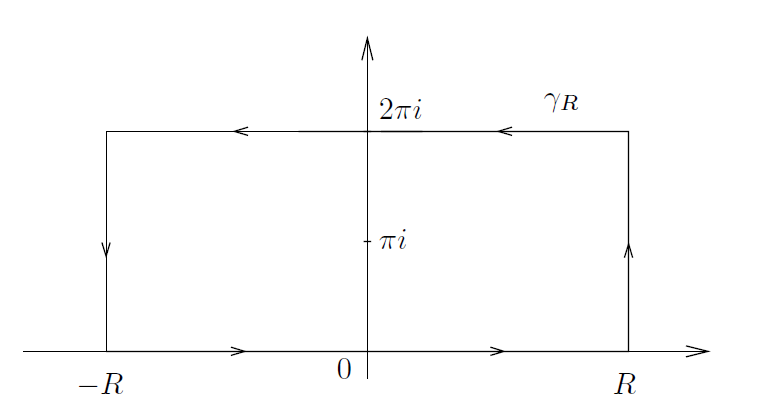
--------------------------------------------图2：例2中的周线 γR ----------------------------------------------------

在矩阵周线 γR 上 f 的分母(denominator) 消没的唯一点是 z = πi 。为了计算f在这点的留数，我们按如下论证：

首先，注意

$\displaystyle (z - \pi{i})f(z) = e^{az}\frac{z - \pi{i}}{1+e^{z}} = e^{az} \frac{z - \pi{i}}{e^{z}-e^{\pi{i}} }$ 。

我们识别出等式右边差商的倒数的特别之处，事实上，

$\displaystyle \lim_{z \rightarrow \pi{i}}\frac{e^{z}-e^{\pi{i}}}{z-\pi{i}}=e^{\pi{i}}=-1$ ,

因为 $e^{z}$ 的导数是其自身。所以，函数 f 在πi处有一个简单极点，其留数

$res_{\pi{i}}f=-e^{a\pi{i}}$ 。

因此，留数公式指的是

(3) $\displaystyle \int_{\gamma {R}}f=-2\pi{i}e^{a\pi{i}}$ 。

现在我们考察 f 在矩阵每一边上的积分。令 $I_{R}$ 表示

$\int_{-R}^{R}f(x)dx$ ，

并令 I 表示我们希望计算的那个积分, 以使得随着 $R \rightarrow \infty$ 而 $I_{R} \rightarrow I$ 。则，可以明确的是，f在矩形上边的积分(具有从右到左的方向)是

$-e^{2\pi{ai}}I_{R}$ 。

最后，若 $A_{R} = \{R + it : 0 \leq t \leq 2\pi \}$ 表示矩形右侧的垂直边，则

$\displaystyle \left |\int_{A_{R}}\right | \leq \int_{0}^{2{\pi}}\left | \frac{e^{a(R + it)}}{1+e^{(R + it)}} \right | dt \leq Ce^{(a-1)R}$ ，

且由于 a < 1 ,则随着 R ⟶∞ 而积分趋近于 0 。类似地，f在矩形左侧的垂直边上的积分也随着 R ⟶∞ 而趋近于0 ，因为它可以使用 $Ce^{-aR}$ 和 a > 1 来界定。因此，在极限中，随着 R ⟶∞ ，恒等式 (3) 将产生

$I - e^{2{\pi}ia}I = -2{\pi}ie^{a{\pi}i}$ ，

据此，我们可以推导出

$\begin{array}{rlc} I &\displaystyle= -2{\pi}{i} \frac{ e^{a{\pi}i}}{1-e^{2{\pi}ia}} \\ \\ &\displaystyle= \frac{2{\pi}i}{e^{{\pi}ia}-e^{(-{\pi}ia)} } \\ \\ &\displaystyle= \frac{\pi}{\sin({\pi}a)} \end{array}$ ，

到此，计算完结。

例子3：

现在，我们计算另一个Fourier变换，即

$\displaystyle \int_{-\infty}^{\infty}\frac{e^{-2{\pi}ix\xi}}{\cosh{(\pi{x})}}dx=\frac{1}{\cosh{({\pi}}\xi)}$ ，

其中，

$\displaystyle \cosh{(z)}=\frac{e^{z}+e^{-z}}{2}$ 。

换句话说，函数 1/cosh(z) 是其自身的Fourier变换,函数 $e^{-{\pi}x^{2}}$ 也具有这种属性(见第2章例1)。为了理解这一点，我们使用一个如下图3所示的矩形周线 γR ，其宽度趋近于无穷大，但其高度宽定。对于一个固定的 ξ∈ℝ ，令

$\displaystyle f(z) = \frac{e^{-2{\pi}iz\xi}}{\cosh{({\pi}z)}}$ ，

并注意到，当 $e^{{\pi}z} = -e^{{-\pi}z}$ 时，即，当 $e^{2{\pi}z} = -1$ 时，函数 f 的分母恰好消没。换言之，f在矩形周线内的仅有极点是位于 α = i/2 和 β = 3i/2 处。为了求得f 在α处的留数，我们注意到

$\begin{array}{rlc} (z - {\alpha}) f(z) & \displaystyle= e^{-2{\pi}iz{\xi}} \frac{2(z - {\alpha})}{e^{{\pi}z} + e^{-{\pi}z}} \\ \\ &\displaystyle= 2e^{-2{\pi}iz{\xi}} e^{{\pi}z} \frac{(z - {\alpha})}{e^{2{\pi}z}- e^{2{\pi}{\alpha}}} \end{array}$ 。

我们识别出等式右边为函数 $e^{2{\pi}z}$ 在 z = α 处的差商(difference quotient)之倒数。因此，

$\displaystyle \lim_{z \rightarrow \alpha}(z - \alpha) f(z) = 2e^{-2{\pi}iz{\xi}} e^{{\pi}z}\frac{1}{2{\pi}e^{2{\pi}\alpha}} = \frac{e^{{\pi}\xi}}{{\pi}i }$ ，

(译注：函数的一阶差商即是函数一阶导数按定义的求法，因此，上式 $\frac{(z - {\alpha})}{e^{2{\pi}z}- e^{2{\pi}{\alpha}}}$ 是函数 $e^{2\pi{z}}$ 在z = α 处的导数之倒数， $e^{2\pi{\alpha}}$ 对α 求一阶导数即是 $2{\pi}e^{2{\pi}\alpha}$ ), 上述即证明了函数 f在α 处具有一个留数为 $\frac{e^{{\pi} \xi}}{{\pi}i}$ 的简单极点。类似地，我们求得 f 在 β 处具有一个留数为 $-\frac{e^{3{\pi}\xi}}{{\pi}i}$ 的简单极点。

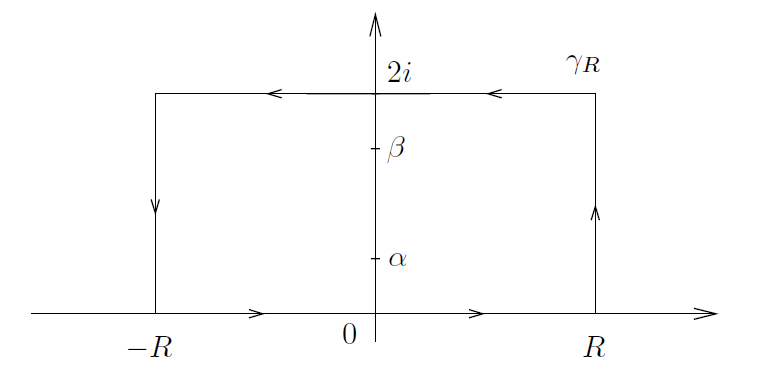
---------------------------------------------------图3: 例3中的周线γR ----------------------------------------------

我们通过证明当 R 趋于无穷大时 f 在垂直边上的积分趋于零的方式，从而略去 f 在垂直边上的积分。事实上，若 z = R + iy (0 ≤ y ≤ 2), 则

$\displaystyle |e^{-2{\pi}iz{\xi}} | \leq e^{4{\pi}|{\xi}|}$ ，

且

$\begin{array}{rlc} |\cosh{(z)}|&\displaystyle= \left | \frac{e^{{\pi}z}+e^{-{\pi}z}} {2} \right | \\ \\ &\displaystyle \geq \frac{1}{2}\bigg | \left |e^{{\pi}z}\right | -\left |e^{-{\pi}z} \right | \bigg | \\ \\ & \displaystyle \geq \frac{1}{2} \left |e^{\pi{R}}-e^{-\pi{R}} \right | \\ \\ & \displaystyle \rightarrow \infty (R \rightarrow \infty) \end{array}$ ，

这就证明了 f 在右侧垂直线段上的积分随 $R \rightarrow \infty$ 而趋于 0 。同样，按类似的论证方法，证明f 在左侧垂直线段上的积分随 $R \rightarrow \infty$ 而趋于0 。最后，我们看到，若用I 表示我们所期望的积分，收 f 在矩形上半部分的积分(按从右向左的方向)是 $-e^{4{\pi}{\xi}}I$ ，其中，我们使用了函数 $\cosh(\pi{\zeta} )$ 以2i为周期这个事实。在极限表达式中，随着 R 趋近于无穷大，留数公式给出

$\begin{array}{rlc} I - e^{4{\pi}{\xi}}I&\displaystyle=2{\pi}i \left (\frac{e^{{\pi}{\xi}}}{{\pi}i}-\frac{e^{3{\pi}{\xi}}}{{\pi}i} \right ) \\ \\ &=-2e^{2{\pi}\xi}(e^{{\pi}\xi}-e^{-{\pi}\xi}) \end{array}$ ，

且由于 $1 - e^{4{\pi}{\xi}} =-e^{2{\pi}\xi}(e^{2{\pi}\xi}-e^{-2{\pi}\xi})$ ，我们求得

$\displaystyle I = 2\frac{e^{\pi\xi}-e^{-\pi\xi}}{e^{2\pi\xi}-e^{-2\pi\xi}}=2\frac{e^{\pi\xi}-e^{-\pi\xi}}{(e^{\pi\xi}-e^{-\pi\xi})(e^{\pi\xi}+e^{-\pi\xi})}=\frac{2}{e^{(\pi\xi}+e^{-\pi\xi})}=\frac{1}{\cosh({\pi}\xi)}$ ,

正如所断言的那样。

事实上，类似的论证建立了如下的公式：

$\displaystyle \int_{-\infty}^{\infty}e^{-2{\pi}ix\xi}\frac{\sin(\pi{a})}{\cosh(\pi{x})+\cos(\pi{a})}dx=\frac{2\sinh(2\pi{a\xi})}{\sinh(2\pi{\xi})}$ (只要 0 < a < 1),

其中， $\displaystyle \sinh(z)=\frac{e^{z}-e^{-z}}{2}$ 。

在上面，我们已经证明了特例 a = 1/2 。这个恒等式可以于确定条带(strip)Poisson核的显式公式(参见第I册书第 5 章中的问题 3)，或者证明两个平方和定理(我们将在第 10 章中看到)。

3. 奇点和亚纯函数(Singularities and meromorphic functions)

回到第1节，我们发现，我们已经陈述了一个函数在奇点附近的分析特征。现在我们将注意力集中到其它孤立奇点类型。令 f 为一个开集Ω上的一个全纯函数(可能除去位于 Ω 内的一点 $z_{0}$ 处)，如果我们可以按某种方式定义位于 $z_{0}$ 处的f ，使得f 成为整个Ω上的全纯函数，则我们称 $z_{0}$ 是 f 的可除奇点(a removable singularity)。

定理 3.1 (基于可除奇点的Riemann定理)

假设f 为一个开集Ω上的一个全纯函数(可能除去位于 Ω 内的一点 $z_{0}$ 处)，若 f 在 $\Omega - \{z_{0}\}$ 上是有界的，则 $z_{0}$ 是一个可除奇点。

证明：

因为问题是局部的，我们可以考虑以 $z_{0}$ 为圆心且其闭包含于 Ω 的一个小圆盘 D 。令 C表示这个圆盘的边界且具有通常的正方向。我们将证明，若 $z \in D$ 且 $z \neq z_{0}$ ，则在定理的假设条件下，我们有

(4) $\displaystyle f (z) = \frac{1}{2\pi{i}}\int_{C}\frac{f(\zeta)}{\zeta-z}d\zeta$ 。

因为应用上一章中的定理5.4可证明等式(4)的右侧在整个D上定义了一个全纯函数，当 $z \neq z_{0}$ 时，这个全纯函数与 f (z)一致，这就给到了我们预期的扩展(extension)。

为了证明公式(4)，我们固定 z∈D 且确保 $z \neq z_{0}$ ，并使用如下图4中所示的熟悉的可构周线。

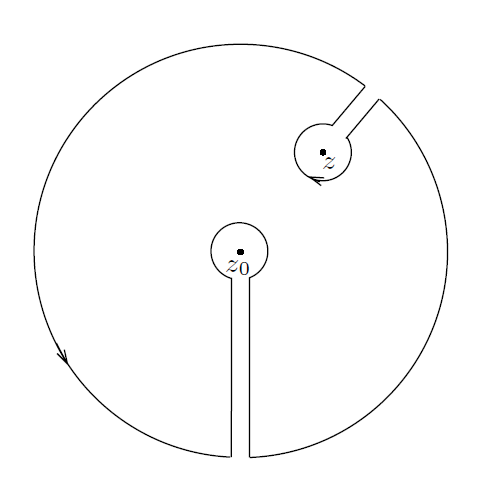
---------------------------------------图4：在Riemann定理证明中使用的多锁眼周线 --------------------------

可以看到，多锁眼周线避开了两个点 z 和 $z_{0}$ 。令窄带(corridor)互相靠近，并最后重叠，则在极限表达式中，我们得到了一个消去表达式(cancellation)：

$\displaystyle \int_{C}\frac{f(\zeta)}{\zeta-z}d\zeta + \int_{\gamma_{\epsilon}}\frac{f(\zeta)}{\zeta-z}d\zeta+\int_{\gamma_{\epsilon}^{'}}\frac{f(\zeta)}{\zeta-z}d\zeta=0$ ，

其中， $\gamma_{\epsilon}$ 和 $\gamma_{\epsilon}^{'}$ 是以 ε 为半径的小圆，且分别以 z 和 $z_{0}$ 为圆心。复制第2章第4节中Cauchy积分公式证明中使用的参数，我们求得

$\displaystyle \int_{\gamma_{\epsilon}}\frac{f(\zeta)}{\zeta-z}d\zeta=-2\pi{i}f(z)$ 。

对于第二个积分，我们使用 f 有界且ε 很小、ζ 远离 z 的假设条件，因此，得到

$\displaystyle \bigg | \int_{\gamma_{\epsilon}^{'}}\frac{f(\zeta)}{\zeta-z}d\zeta \bigg | \leq C\epsilon$ 。

令 ε 趋近于0 即可证明我们的论点(contention),并推导出扩展公式(4)的证明。

令人惊讶的是，我们可以根据函数在奇点邻域中的行为从Riemann定理中推导出极点的特征。

推论 3.2 假设 f 在 $z_{0}$ 点有一个孤立奇点。则当且仅当随着 $z \rightarrow z_{0}$ 而有 $|f(z)| \rightarrow \infty$ 时， $z_{0}$ 是 f 的一个极点。

证明：

若 $z_{0}$ 是一个极点，则我们知道，1/ f 在 $z_{0}$ 点有一个零，因此，当 $z \rightarrow z_{0}$ 时有 $|f(z)| \rightarrow \infty$ 。反之，假设这个条件成立。则 1/ f 在点附近有界，事实上，当 $z \rightarrow z_{0}$ 时有 $1/| f(z)| \rightarrow 0$ 。因此，1/ f 在 $z_{0}$ 处有一个可除奇点，并且在那里一定会消没。这就证明了反之的情况，即 $z_{0}$ 是一个极点。

孤立奇点属于3种分类之一：

$\bullet$ 可除奇点(Removable singularities)( f 在 $z_{0}$ 点附近有界)；

$\bullet$ 极点奇点(Pole singularities) (随着 $z \rightarrow z_{0}$ 而 $|f(z)| \rightarrow \infty$ )；

$\bullet$ 本征奇点(Essential singularities)。

在默认情况下，不可除的或者极点型的任意奇点均定义为本征奇点。例如，在第1节的初开头讨论的函数 $e^{1/z}$ 在 0 处具有一个本征奇点。我们已经观察到该函数在原点附近的“狂野(wild)”行为。与可除奇点或极点附近的全纯函数的受控行为相反，全纯函数在本征奇点附近表现得不稳定(erratically)是其典型特征。下一个定理阐明了这一点。

定理 3.3 (Casorati-Weierstrass) 若 f 在穿孔圆盘(punctured disc) $D_{r}(z_0) - {z_0}$ 上是全纯的，且在 $z_{0}$ 处具有一个本征奇点。则 $D_{r}(z_0) - {z_0}$ 在 f 下和像在复平面上是紧致的(dense)。

证明：

我们按反证法进行论证。假设 f 的范围不是紧的，因此，存在 w ∈ ℂ 和 δ > 0使得

$| f (z) - w | > \delta$ (对于任意 $w \in D_{r}(z_0) - {z_0}$ ) 。

因此，我们可以在 $D_{r}(z_0) - {z_0}$ 上定义一个新函数

$\displaystyle g( z ) = \frac{1}{f(z)-w}$ ，

它在这个穿孔圆盘上是全纯的且以 1/δ 为界。因此，根据定理 3.1 函数 g 在 $z_{0}$ 处有一个可除奇点。若 $g(z_{0}) \neq 0$ ，则 f (z) – w 在 $z_{0}$ 处是全纯的，这与假设 $z_{0}$ 是一个本征奇点矛盾。在 $g(z_{0})=0$ 这种情况下，则 f (z) – w 在 $z_{0}$ 处有一个孔，这也与 $z_{0}$ 处的奇点特征矛盾。因此，定理得证。

事实上，Picard证明了一个更强的结果。他证明，在上述定理的假设下，函数 f 无限次地取每个复值，最多有一次例外。虽然我们不会证明这个显著的结果，但我们将在后面的章节中对整个函数的研究中得出一个更简单的版本。请参阅第 5 章中的练习 11。

现在我们回到仅有极点作为孤立奇点的函数。对于一个开集 Ω上的函数 f ，若存在一个点序列 $\{ z_{0} ,z_{1} ,z_{2} , ...\}$ 在Ω 中具有无限的点，并使得

( i ) 函数 f 在 $\Omega-\{ z_{0} ,z_{1} ,z_{2} , ...\}$ 上是全纯的，和

( ii ) f 在点 $\{ z_{0} ,z_{1} ,z_{2} , ...\}$ 处具有极点，

则 f 是亚纯函数(meromorphic)。

讨论扩充复平面中的亚纯函数也很有用。若一个函数对于任意大的 z 值是全纯的，我们可以使用我们用来对 z 有限值处的奇点进行分类的三重区分来描述其在无穷远处的行为。因此，若 f 对于任意大的 z 值是全纯的，我们可以考虑 F ( z ) = f (1/z) , 现在它在原点的删除领域中是全纯的，若 F 在原点处有一个极点，我们称 f 在无穷远处有一个极点(a pole at infinity)。类似地，根据 F 在 0 点的相应行为，我们可以称f 在无穷远处有一个本征奇点(an essential singularity at infinity)、或者在无穷远处有一个可除奇点(a removable singularity at infinity)(因此，也是全纯的)。复平面中的亚纯函数，如果在无穷远处全纯或在无穷远处具有极点，则称其在扩充复平面中是亚纯函数(meromorphic in the extended complex plane)。

在这个阶段我们回到本章开头提到的原理。在这里我们可以看到它最简单的形式。

定理 3.4 在扩充复平面上的亚纯函数是比率函数(rational function)。

证明：

假设 f 在扩充复平面上是全纯的。则 f (1/z) 在 0 点有一个极点或者一个可除奇点，并且在任一种情况下，在原点的一个删除领域内它一定是全纯的。因此，函数 f 在平面上仅有有限多个极点(比如说，位于 $z_{1} ,...,z_{n}$ 处)。这种思想就是从 f 中减去其所有极点的主要部分，包括其无穷远处的极点。在每个极点 $z_{k}\in \mathbb{C}$ 附近，我们可以写成

$f (z) = f_{k}(z) + g_{k}(z)$ ，

其中， $f_{k}(z)$ 是 f 在 $z_{k}$ 点处的主要部分，且 $g_{k}$ 在 $z_{k}$ 的(全)领域中是全纯的。且 $f_{k}$ 是一个按 $1/( z - z_{k})$ 的多项式。类似地，我们可以写成

$f(1/z)=\hat{f}_{\infty}(z)+\hat{g}_{\infty}(z)$ ，

其中， $\hat{g}_{\infty}$ 在原点的领域内是全纯的，且 $\hat{f}_{\infty}$ 是 f (1/z) 在 0 点处的主要部分，即，按 1/z 的多项式。最后，令 $f_{\infty}(z)=\hat{f}_{\infty}(1/z)$ 。

我们断言函数 $H = f - f_{\infty} - \sum_{k=1}^{n}f_{k}$ 是复可积函数且有界。事实上，在极点 $z_{k}$ 的附近我们减去 f 的主要部分，因此，函数 H在那儿有可除奇点。此外，H (1/z)对于 0 附近的z有界，因为我们从位于 ∞ 处的极点减去了主要部分。这证明了我们的观点，根据Liouville定理，我们推断出 H 是常量。根据 H 的定义，我们发现 f 是一个比率函数，正如所证明的。

请注意，因此，比率函数通过规定其零点和极点的位置和重数(multiplicities)来确定乘法常数。

3.1 Riemann 球面(The Riemann sphere)

扩充复平面(由复数 ℂ 和位于无穷远处的点构成)有一个方便的几何解释，我们在此作简要讨论。

考虑具有坐标( X,Y,Z ) 的Euclid空间 $\mathbb{R}^{3}$ ，其中，XY 平面等同于 ℂ 。我们用 𝕊 表示球心位于( 0,0,1/2 )且半径为 1/2 的球体。这个球体的直径是单位直径，并且如图5所示位于复平面原点的上方。此外，我们令 𝒩 = (0,0,1)表示球体的北极。

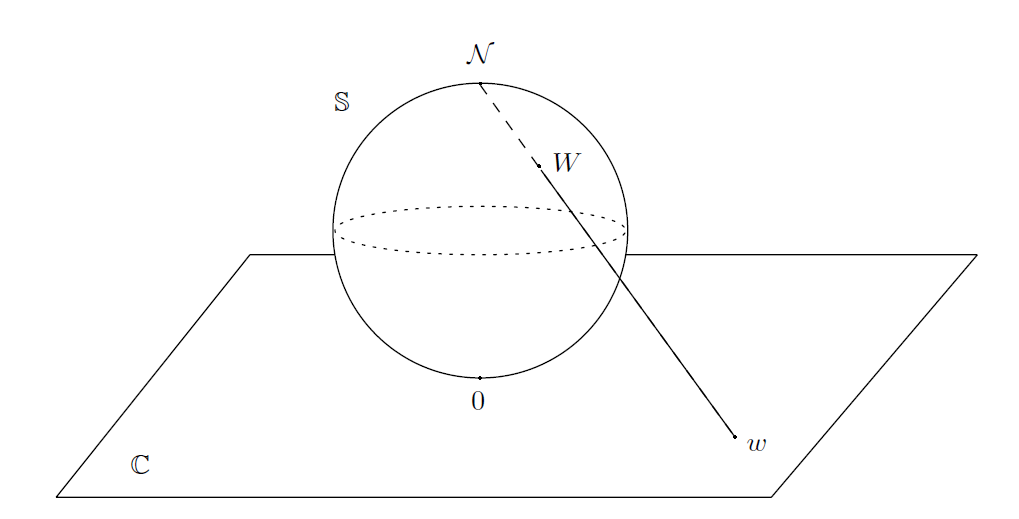
-----------------------图5: Riemann球体 𝕊 及其立体投影(stereographic projection)----------------------

已经 𝕊 上不同于北极点的任意点 W = (X,Y,Z ), 连接 𝒩 和 W 的直线与 XY 平面相交与一点，我们用 w = x + iy 表示这一点；则称 w 为 W 的立体投影(stereographic projection)(见图5)。反之，已知 ℂ 中任意点 w ，连接 𝒩 和 w = ( x, y, 0) 的直线与球面相交于 𝒩 和别一点，我们称这一点为 W 。这个几何结构给出了一个穿孔球面 𝕊 – { 𝒩 } 和复平面之间的双射对应；用公式解析地表述为

$x=\frac{X}{1-Z}$ 和 $y=\frac{Y}{1-Z}$ ,

根据 𝒲 给出 w ，以及

$\displaystyle X=\frac{x}{x^{2}+y^{2}+1},Y=\frac{x}{x^{2}+y^{2}+1},Z=\frac{x^{2}+y^{2}}{x^{2}+y^{2}+1}$ ，

根据 w 给出 W 。在直观上，我们已经将得平整面封装到穿孔球面 𝕊 – { 𝒩 } 。

随着点 w 在 ℂ 中趋向于无穷大(在| w |⟶∞的意义上)，这个相对应的点 W 在 𝕊 上任意接近 𝒩 。这个简单的观察表明， 𝒩 成为所谓“无穷远处的点”的天然候选。无穷远处的点等同于 𝕊 上的点 𝒩，我们看到，扩充复平面可以被视为完全的二维球体 𝕊，称为Riemann球体(Riemann sphere)。由于这种构造通过添加一个点将无界集 ℂ 纳入紧致集 𝕊，因此Riemann球体有时被称为 ℂ 的一点紧化(one-point compactification)。

这种解释的一个重要结果如下：虽然无穷远点在与 ℂ 分开考虑时需要特别注意，但它现在发现自己与 𝕊 上的所有其他点处于同等地位。特别是，扩展复平面上的亚纯函数可以被认为是从 𝕊 到自身的映射，其中极点的图像现在是 𝕊 上的一个易于处理的点，即 𝒩。由于这些原因(以及其他原因)，Riemann球体为 ℂ 的结构以及亚纯函数理论提供了良好的几何上的洞悉。

4. 幅角原理及其应用(The argument principle and applications)

我们用几个评述提前进行对数讨论(见第6节)。通常，函数 $\log {f(z)}$ 是“多值的(multiple-valued)”，因为它不能被无歧义地定义于 $f (z) \neq 0$ 的集合上。然而，要定义它，就一定等于 $\log{|f(z)|}+i\arg{f(z)}$ ，其中， $\log{|f(z)|}$ 是通常的正数量 | f (z) | 的实变量对数(因此，定义无歧义)，而 $\arg{f(z)}$ 是某种参数确定量(最大为 2π 的加法整数倍)。注意，在任意情况下， $\log{f(z)}$ 的导数都是 $f {'}(z)/f (z)$ ，这是一个单值函数，而积分

$\displaystyle \int_{\gamma}\frac{f^{'}(z)}{f(z)}dz$

可以被解释为当 z 穿过曲线 γ 时 f 参数的变化。此外，假设曲线是闭合的，这种参数变化完全取决于 f 在γ 内的零点和极点。现在，我们将这一事实公式化为一个确切的定义。

首先，当加法公式

$\log{f_{1}f_{2}}=\log{f_{1}}+\log{f_{2}}$

通常不成立的时候(正如我们下面将会看到的那样)，这个加法可以恢复为对应的积分，我们从此开始介绍。这一点可以从下面的观察得到证实：

$\displaystyle \frac{(f_{1}f_{2})^{'}}{f_{1}f_{2}}=\frac{f_{1}^{'}f_{2}}{f_{1}f_{2}}+\frac{f_{1}f_{2}^{'}}{f_{1}f_{2}}=\frac{f_{1}^{'}}{f_{1}}+\frac{f_{2}^{'}}{f_{2}}$ ，

上式可推广为

$\displaystyle \frac{(\prod_{k=1}^{N}f_{k})^{'}}{\prod_{k=1}^{N}f_{k}}=\sum_{k=1}^{N}\frac{f_{k}^{'}}{f_{k}}$ 。

我们应用些公式如下，若 f 是全纯的且在 $z_{0}$ 点有一个 n 限 0 点，我们可以写成

$f ( z ) = (z-z_{0})^{n} g(z )$ ，

其中，g 是一个全纯函数且在 $z_{0}$ 的领域内无处消没，因此，

$\displaystyle \frac{f^{'}(z)}{f(z)}=\frac{n}{z-z_{0}}+G(z)$ ，

其中，G(z) = g ’(z)/g (z) 。这个结论在于，若 f 在 $z_{0}$ 点有一个 n 限极点，即，若 $f ( z ) = (z-z_{0})^{-n} h(z )$ , 则

$\displaystyle \frac{f^{'}(z)}{f(z)}=\frac{-n}{z-z_{0}}+H(z)$ 。

因此，若 f 是全纯的，则函数 f ‘/ f 将在f 的0 点和极点有简单的极点，并且留数只是 f 的零阶或 f 极点的负阶。结果，应用留数公式给出以下定理。

定理 4.1 (幅角原理) 若 f 在包含圆 C及其内部的开集中是亚纯的，若 f 在 C 上没有极点且永远不会消没，则

$\frac{1}{2\pi {i}}\int_{C}\frac{f{'}(z)}{f(z)}dz$ = ( C 内 f 的零点数 ) - ( C 内 f 的极点数 ) ，

其中零点和极点以其重数进行计数。

推论 4.2 以上定理对于可构周线成立。

作为幅角原理的应用，我们将证明一般理论中有趣的三个定理。第一个，Rouché定理，在某种意义上是一种连续性的表述。它指的是，全纯函数可以在不改变其零点数量的情况下被轻微扰动(perturbed)。然后，我们证明了开映射定理(open mapping theorem)，该定理指出全纯函数将开集映射到开集，这是一个重要的性质，再次显示了全纯函数的特殊性质。最后，最大模原理(maximum modulus principle)让人想起(实际上暗示)调和函数的相同性质：开集 Ω 上的非常数全纯函数无法在Ω内部达到最大值。

定理 4.3 (Rouché定理) 若 f 和g在包含圆 C及其内部的开集中是全纯的，若

| f ( z ) | > | g( z ) | ( 对于任意 z∈C ),

则 f 和 f + g 在圆 C 内具有相同数量的零点。

证明：

对 t∈[0,1] 定义

$f_{t}( z ) = f ( z ) + t g( z )$ ，

因此， $f_{0} = f$ 和 $f_{1} = f + g$ 。令 $n_{t }$ 表示 $f_{t }$ 在圆内按重数计算的0点数量，因此，特别是， $n_{t}$ 是整数。对于 z∈C ，条件 | f ( z ) | > | g( z ) | 显然意味着， $f_{t}$ 在圆上没有0点，幅角原理表明，

$\displaystyle n_{t}=\frac{1}{2\pi{i}}\int_{C}\frac{f_{t}^{'}(z)}{f_{t}(z)}dz$ 。

为了证明 $n_{t}$ 是常数，只需证明其是 t 的连续函数即可。则我们可以论证，若 $n_{t}$ 不是常数，中值定理(intermediate value theorem)确保某些具有 $n_{t_{0}}$ 不是整数的 $t_{0} \in [0,1]$ 存在，这与对于任意 t ， $n_{t}\in \mathbb{Z}$ 相矛盾。

为了证明 $n_{t}$ 的连续性，我们观察到， $f_t^{' }(z)/ f_t(z)$ 对于 t∈[0,1] 和 z∈C 是联合连续的，这种联合连续性可以根据它对于分子(numerator)和分母(denominator)都成立，以及我们的假设确保了 $f_{t}( z )$ 不会在 C上消没这个事实推导出。因此， $n_{t }$ 是整数值并且连续，且一定是常量。我们推断出 $n_{0} = n_{1}$ , 这是Rouché定理。

现在我们来了解全纯函数的一个重要几何性质，当我们将它们视为映射(即，将复平面中的区域映射到复平面)时，就会出现该几何性质。

对于一个映射，若它将开集映射到开集，则称其为开的(open)映射。

定理 4.4 (开映射定理) 若 f 在区域Ω 中是全纯的且非常量，则 f 是开的。

证明：

令 $w_{0}$ 属于f 的像(比如， $w_{0}=f(z_{0})$ )。我们一定可以证明， $w_{0}$ 处的所有点 w 也属于 f 的像。

定义 $g( z ) = f ( z ) -w$ 并记为

$\displaystyle g(z) = ( f ( z ) - w_{0} ) + ( w_{0} - w ) = F(z) + G(z)$ 。

现在选取 δ > 0 使得圆盘 $| z - z_{0} | \leq \delta$ 含于 Ω 中，并且在圆 $| z - z_{0} |= \delta$ 上 $f ( z ) \neq w_{0}$ 。然后我们可以选择 ε > 0 使得我们有，在圆 $| z - z_{0} |= \delta$ 上 |F(z) | > | G(z)|，并根据 Rouché 定理，我们推断出 g = F + G 在圆内有一个零点，因为 F 在圆内有一个零点。

下一个结论与全纯函数的大小有关。我们将开集 Ω 中全纯函数 f 的最大值称为其绝对值 | f | 在 Ω 中的最大值。

定理 4.5 (最大模原理)(Maximum modulus principle) 若 f 在Ω 中是一个非常量全纯函数，则 f 在Ω 中在不能获得最大值。

证明：

假设 f 在 $z_{0}$ 点确实可以获得最大值。因为 f 是全纯的，它是一个开映射，因此，若 D ⊂ Ω 是一个圆心位于 $z_{0}$ 点的小圆盘，其像 f (D) 是一个开集并且包含 $f(z_{0})$ 。这就说明，存在点 z∈D 使得 $| f (z) | > | f (z_{0})|$ ，这与假设矛盾。

推论 4.6 若Ω 是一个具有紧闭包 $\overline{\Omega}$ 的区域。若 f 在Ω 上是全纯的且在 $\overline{\Omega}$ 上是连续的，则

$\displaystyle \sup_{z\in \Omega}|f(z)| \leq \sup_{z\in \overline{\Omega}-\Omega}|f(z)|$ 。

事实上，由于 f (z) 在紧集 $\overline{\Omega}$ 上是连续的，则 f (z) 在 $\overline{\Omega}$ 中获得其最大值；但在Ω中却不能，因为 f 是非常量。若 f 是常量,则这个结论是平凡的。

评注： $\overline{\Omega}$ 是紧致的(即，有界的)这个假设对这个结论而言至关重要。我们给出一个将在第4章开始学习的与考量相关的例子。令 Ω 为开第一像限(quadrant),以正的半直线 x ≥ 0 和相应的虚 y ≥ 0 为界。考虑 $\displaystyle F(z) = e^{-iz^{2}}$ ，则 F 显然是复可积函数并且显然在 $\overline{\Omega}$ 上是连续的。此外，在两个边界轴 z = x和 z = iy 上 | F(z)| = 1 。然而，F(z) 在Ω中是无界的，因为，例如，若 $z = r\sqrt{i} = re^{i\pi/4}$ , 则我们有 $F(z) = e^{r^{2}}$ 。

5. 同伦和简单连通域(Homotopies and simply connected domains)

Cauchy定理的一般式以及多值函数分析的关键在于，理解在什么域我们可以定义一个已知全纯函数的原函数。注意对数研究的相关性，它以1/z 的原函数出现。本质问题不仅在于局部，而且也在于全局。对其阐明(elucidation)要求同伦(homotopy)的概念，以及由此产生的简单连通的思想。

令 $\gamma_{0}$ 和 $\gamma_{1}$ 开集Ω 中的两条具有相同端点的曲线。因此，若 $\gamma_{0}(t)$ 和 $\gamma_{1}(t)$ 是两个定义于[a,b] 上的参数化表达式，则我们有

$\gamma_{0}(a) = \gamma_{1}(a) = \alpha$ 和 $\gamma_{0}(b) = \gamma_{1}(b) = \beta$ 。

若对于每一个 0 ≤ s ≤ 1 ，存在一条曲线 $\gamma_{s} \subset \Omega$ ，可以用定义于 [a,b] 上的 $\gamma_{s}(t)$ 参数化，使得对每一个 s ，有

$\gamma_{s}(a) = \alpha$ 和 $\gamma_{s}(b) = \beta$ ,

以及对于任意 t∈[a,b],有

$\gamma_{s}(t)|_{s=0} = \gamma_{0}(t)$ 和 $\gamma_s(t)|_{s=1} = \gamma_{1}(t)$ ，

则称这两条曲线在 Ω 中是同伦的(homotopic)。此外， $\gamma_{s}(t)$ 在 s∈[0,1] 和 t∈[a,b] 中应当是联合连续的。

大致地讲，对于两条曲线，若其中一条曲线可以通过连续变换变形为另一条曲线而不离开Ω，则这两条曲线是同伦的(如图 6所示)。

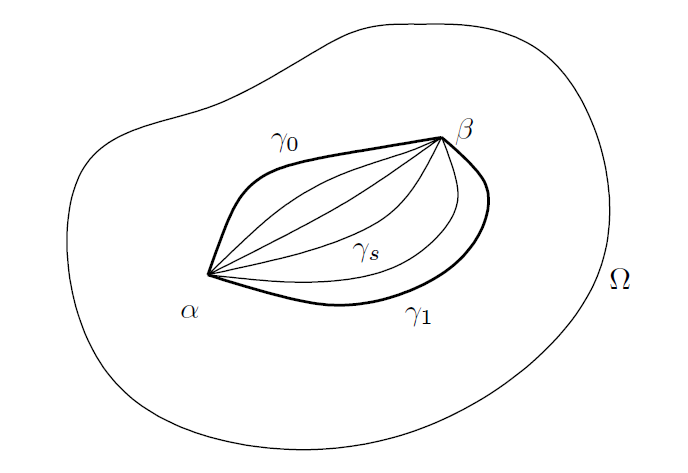
---------------------------------------------------------图6: 曲线的同伦--------------------------------------------------

定理 5.1 若 f 是Ω 中的全纯函数，只要 $\gamma_{0}$ 和 $\gamma_{1}$ 这两个函数在Ω 中是全纯的，则

$\displaystyle \int_{\gamma_{0}}f(z)dz = \int_{\gamma_{1}} f(z)dz$ 。

证明：

证明的关键在于证明若这两条曲线紧密靠近且具有相同的端点，则在这两条曲线上的积分是相等的。我们记得，根据定义，函数 $F(s,t) = \gamma_{s}(t)$ 在[0,1]×[a,b] 是连续的。特别地，由于 F 的像(我们用K表示)是紧的，存在ε > 0 使得半径为 3ε 圆心位于 F 的像中的一点的每一个圆盘都含于 Ω 中。否则，对于每一个 𝓁 ≥ 0 ，存在点 $z_{\ell}\in K$ 以及Ω 的补集中的点 $w_{\ell}$ 使得 $|z_{\ell} - w_{\ell}| < 1/{\ell}$ 。按照K的紧致性，存在一个 $\{\ell\}$ 的子序列(比如说 $\{ z_{\ell_{k}}\}$ )收敛于一点 z∈K⊂Ω ，按构造，我们一定也有 $w_{\ell_{k}} \rightarrow z$ ，且因为 $\{w_{\ell}\}$ 位于Ω的补集中且是闭合的，我们一定也有 $z \in \Omega^{c}$ 。这是矛盾的。

在求得具有预期属性的 ε 之后，我们可以(根据 F 的一致连续性)选择 δ 使得

$\displaystyle \sup_{t \in [a,b]}\bigg | \gamma_{s_{1}(t)}- \gamma_{s_{2}(t)} \bigg |< \epsilon$ ( 只要 $|s_{1}-s_{2}|< \delta$ ) 。

固定 $s_{1}$ 和 $s_{2}$ 且 $|s_{1}-s_{2}|< \delta$ 。则我们选择半径 2ε 的圆盘 $\{ D_{0} ,..., D_{n} \}$ ，以及 $\gamma_{s_{1}}$ 上的连贯点(consecutive) $\{ z_{0} ,..., z_{n+1} \}$ 和 $\gamma_{s_{2}}$ 上的连贯点 $\{ w_{0} ,..., w_{n+1} \}$ ，使得这些圆盘的合并覆盖这两条曲线，以及

$z_{i} ,z_{i+1} ,w_{i} ,w_{i+1} \in D_{i}$ ，

这种情况如图7所示。

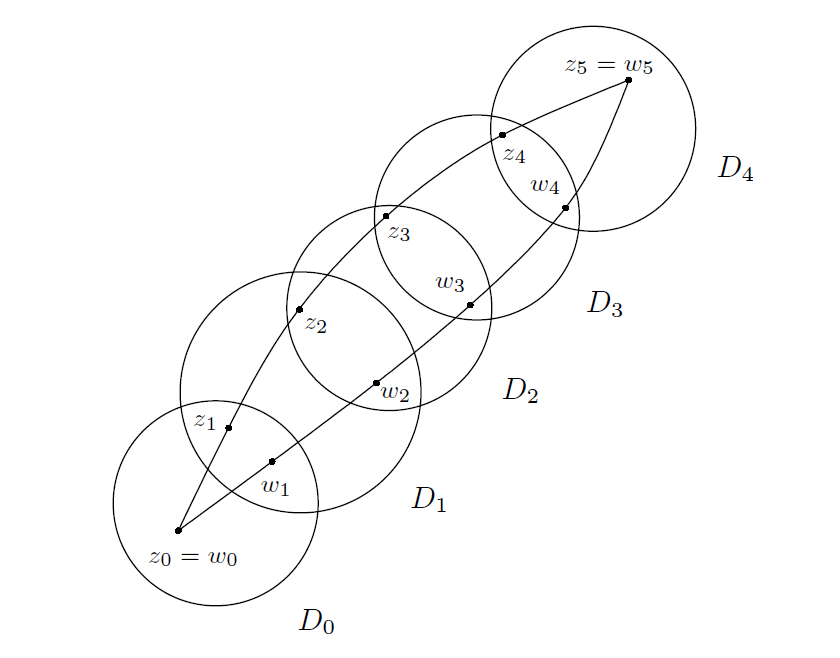
---------------------------------------------------图7：用圆盘覆盖两条相邻曲线-----------------------------------

此外，我们选择 $z_{0}=w_{0}$ 作为曲线的起始端点， $z_{n+1} = w_{n+1}$ 作为共同的末端点。在每一个圆盘 $D_{i}$ 上，令 $F_{i}$ 表示 f 的原函数(第2章定理2.1)。在 $D_{i}$ 和 $D_{i+1}$ 的交集上， $F_{i}$ 和 $F_{i+1}$ 是同一函数的两个原函数，因此，它们之间的差异一定只在于常量(比如， $c_{i}$ )。因此，

$F_{i+1}(z_{i+1}) - F_{i}(z_{i+1}) = F_{i+1}(w_{i+1}) - F_{i}(w_{i+1})$ ,

故而

(5) $F_{i+1}(z_{i+1}) - F_{i}(z_{i+1}) = F_{i+1}(w_{i+1}) - F_{i}(w_{i+1})$ 。

这意味着

$\begin{array}{rlc} \displaystyle \int_{\gamma_{s_{1}}}f-\int_{\gamma_{s_{2}}}f&\displaystyle=\sum_{i=0}^{n}\left [ F_{i}(z_{i+1}) - F_{i}(z_{i}) \right ] - \sum_{i=0}^{n}\left [ F_{i}(w_{i+1}) - F_{i}(w_{i}) \right ] \\\\ &\displaystyle=\sum_{i=0}^{n}\left [ F_{i}(z_{i+1}) - F_{i}(w_{i+1})-(F_{i}(z_{i})-F_{i}(w_{i}) \right ] \\\\ &\displaystyle=F_{n}(z_{n+1})-F_{n}(w_{n+1})-(F_{0}(z_{0})-F_{0}(w_{0})) \end{array}$ ，

因为这是由于(5)的消去性。由于 $\gamma_{s_{1}}$ 和 $\gamma_{s_{2}}$ 具有相同的起点和止点，所以，我们已经证明了

$\displaystyle \int_{\gamma_{0}} f = \int_{\gamma_{1}} f$ 。

通过二次划分区间[0,1]为长度不超过δ 的子区间 $[s_{i},s_{i+1}]$ ,我们可以经过有限多次从 $\gamma_{0}$ 到 $\gamma_{1}$ 应用以上论证方法，从而定理得证。

对于复平面上的区域Ω ，若Ω 中任意两条具有相同端点的成对曲线是同伦的，则此区域Ω是简单连通的(simply connected)。

例子1：

一个圆盘D 是简单连通的。事实上，若 $\gamma_{0}(t)$ 和 $\gamma_{1}(t)$ 是两条横亘于 D 中的两条曲线，我们可以定义 $\gamma_{s}(t)$ 为

$\displaystyle \gamma_s(t) = (1 - s)\gamma_{0}(t) + s\gamma_{1}(t)$ 。

注意，若 0 ≤ s ≤ 1 ，则对于每一个 t ，点 $\gamma_{s}(t)$ 在连接 $\gamma_{0}(t)$ 和 $\gamma_{1}(t)$ 的线段上，因此也就在D中。若将 D 换成矩形、或者更一般地换成任意开的凸面集(open convex set),则同样的论证依然有效(见练习21。)

例子2：

狭窄平面(slit plane) $\Omega = \mathbb - \{(-\infty,0]\}$ 是简单连通的。对于Ω 中的一对曲线 $\gamma_{0}$ 和 $\gamma_{1}$ ，我们记为 $\gamma_{j}(t) = r_{j}(t)e^{i\theta_{j} (t)} ( j = 0,1 )$ 且 $r_{j}(t)$ 连续且严格为正， $\theta_{j}(t)$ 连续且 $|\theta_{j} (t)|< \pi$ 。则，我们可以定义 $r_{s}(t)$ 为 $r_{s}(t) e^{i\theta_{s} (t)}$ ，其中，

$r_{s}(t) = (1 - s)r_{0}(t) + sr_{1}(t)$ 和 $\theta_{s} (t) = (1 - s)\theta_{0}(t) + s\theta_{1}(t)$ 。

则只要 0 ≤ s ≤ 1 ，我们就有 $\gamma_{s}(t) \in \Omega$ 。

例子3：

经过一些努力，我们可以证明可构周线的内部是简单连接的。这就要求我们将内部划分为几个子区域。练习 4 给出了论证的一般形式。

例子4：

与前面的例子相反，穿孔平面 ℂ - {0} 不是简单连通的。直观地，考虑原点位于两者之间的两条曲线。连续地从一条曲线过渡到另一条曲线而不超过 0 是不可能的。这一事实的严格证明需要进一步的结果，很快就会给出。

定理 5.2 在一个简单连通域内的任意全纯函数都有一个原函数。

证明：

固定 Ω 内的一个点 $z_{0}$ 并定义

$\displaystyle F(z) = \int_{\gamma} f (w)dw$ ，

其中，积分在 Ω 内连接 $z_{0}$ 到 $z_{1}$ 的任意曲线上进行。这种定义独立于曲线的选择，因为 Ω是简单连通的，而若 $\widetilde{\gamma}$ 是 Ω内连接 $z_{0}$ 到 $z_{1}$ 的另一条曲线，根据定理 5.1 ，我们应有

$\displaystyle \int_{\gamma} f (w)dw = \int_{\widetilde{\gamma}} f (w)dw$ 。

现在，我们可以记为

$\displaystyle F( z + h ) - F(z) = \int_{\eta} f (w)dw$ ，

其中，η 是连接 z 到 z + h 的线段。如第2章定理2.1 的证明论证一样，我们求得

$\displaystyle \lim_{h \rightarrow 0 }{\frac{F( z + h ) - F(z)}{h}} = f (z)$ 。

最终，我们获得了Cauchy定理的如下版本。

推论 5.3 若 f 在简单连通域 Ω中是全纯的，则对于Ω中的任意闭合曲线 γ,有

$\displaystyle \int_{\gamma} f (z)dz = 0$ 。

根据原函数存在性立即可得出此结论。

事实上，穿孔平面现在不是简单连接的，这一事实严格地根据 1/z 在单位圆上的积分为 2πi 而不是 0 的观察结果得出。

6. 复对数(The complex logarithm)

假设我们希望定义一个非零复数的对数。若 $z = re^{i\theta}$ , 我们希望对数是指数的逆，则很自然地设

$\log{z} = \log{r} + i\theta$ 。

在此处及下面，我们约定 $\log{r}$ 表示正整数 r的标准对数(注：根据标准对数的定义，我们指的是出现在初等积分正数的自然对数)。上述定义的麻烦在于，θ仅在2π 的整数倍范围内是唯一的。然而，对于已经的 z ，我们可以固定选择一个 θ ，并且若 z 的任意变动，唯一地取决于所选择的θ (假设我们要求θ 连续地随 z 变动)。因此，“在局部上”，我们可以给出对数的一个无歧义的定义，但是，这种定义在“全局上”无效。例如，若 z 从1开始,然后绕原点转一圈(winds)返回到1 ，对数不会回到其原点值，而是相差2πi的整数倍，因此，不是“单值的。” 为了使对数作为单值函数有意义，我们必须限定我们在其上定义对数的集合。这就是所谓的对数的枝(branch)或者叶(sheet)的选择。

我们对上面给出的简单连通域的讨论导致了对数函数枝的自然全局定义。

定理 6.1 假设 Ω 是简单连通的且 1∈Ω 和 0 ∉ Ω。则在Ω 中存在对数的枝 $F(z)=\log_{\Omega}(z)$ 使得

( i ) F 在 Ω 中是全纯的。

( ii ) 对于任意 $z\in \Omega$ ， $e^{F(z)} = z$ 。

( iii ) 只要 r 是实数且邻1，就有 F(r ) = r 。

换句话说，每个枝 $\log_{\Omega}(z)$ 都是为正数定义的标准对数的一个扩展。

证明：

我们将构造一个函数 F 作为函数 1/z 的原函数。因为 0 ∉ Ω ，则函数 f(z) = 1/ z 在Ω 上是全纯的，我们定义

$\displaystyle \log_{\Omega}(z) = F(z) = \int_{\gamma} f (w)dw$ ,

其中，γ 是 Ω 中连接 1 到 z 的任意曲线。因为 Ω 是简单连通的，所以定义不依赖于所选择的路径。按照同定理5.2的证明相同的论证，我们求得 F 是全纯的，并且对于任意 z ∉ Ω ，F ’(z) = 1/ z ，这就证明了 ( i )。为了证明 ( ii )，只需证明 $ze^{-F(z)} = 1$ 即可。为此，我们对上式的左边进行微分，得到

$\displaystyle \frac{d}{dz}(ze^{-F(z)})=e^{-F(z)}-zF^{'}(z)e^{-F(z)}=(1-zF^{'}(z))e^{-F(z)}=0$ 。

由于Ω 是连通的，我们(根据第1章推论3.4 ) 推断出 $ze^{-F(z)}$ 是常量。计算出在 z = 1 处的这个表达式，并注意到 F (1) = 0 ,因此，我们求得这个常量一定是 1 。

最后，若 r 是实数并接近1 ,我们可以在实轴上选择从 1 到 r 的线段作为路径，根据标准对数的常规公式，使得

$\displaystyle F(r) = \int_{1}^{r}\frac{1}{x}dx = \log{r}$ 。

这样就完成了对定理的证明。

例如，在狭窄平面 $\Omega = \mathbb{C} - \{(-\infty,0]\}$ 中，我们有对数的主枝(principal branch)

$\log{z}=\log{r}+i\theta$ ，

其中， $z=re^{i\theta}$ 且 |θ | < π 。(在此，我们去掉了下标 Ω ，并简记为 $\log{z}$ 。) 为了证明这一点，我们使用如图8所示的积分路径 γ 。

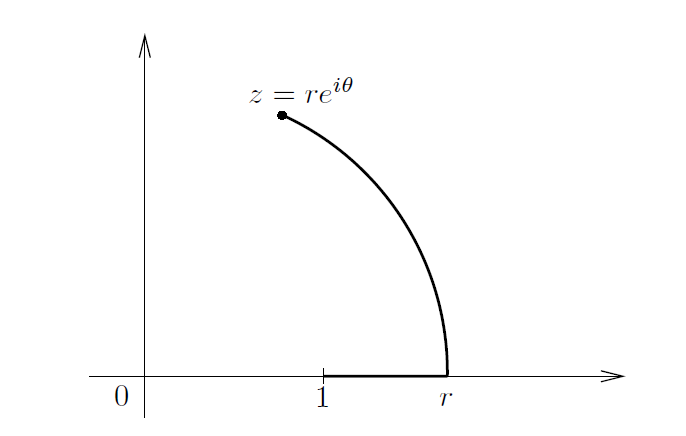
-----------------------------------------------图8：对数主枝积分路径---------------------------------------------

若 $z = re^{i\theta}$ 且 |θ | < π ，路径为从 1 到 r 的线段和从 r 到 z 的弧 η 构成。则

$\begin{array}{rlc} \log{z} &\displaystyle= \int_{1}^{r}\frac{dx}{x} + \int_{\eta}\frac{dw}{w} \\ \\ &\displaystyle= \log{r}+\int_{1}^{\theta}\frac{ire^{it}}{re^{it}}dt \\ \\ &\displaystyle= \log{r}+i\theta \end{array}$ 。

一个重要的观察是，通常

$\displaystyle \log{z_{1}z_{2}} \neq \log{z_{1}}+\log{z_{2}}$ 。

例如，若 $z_{1} = e^{2{\pi}i/3} = z_{2}$ ，则对于对数的主枝，我们有

$\displaystyle \log{z_{1}}=\log{z_{2}}=\frac{2\pi{i}}{3}$ ，

因为 $z_{1}z_{2}=e^{-2\pi{i}/3}$ , 我们有

$\displaystyle \frac{-2\pi{i}}{3} = \log{(z_{1} z_{2}) } \neq \log{z_{1}} + \log{z_{2}}$ 。

最后，对于对数主枝，下面的Taylor 展式成立

(6) $\displaystyle \log{(1+z)} = z - \frac{z^{2}}{2} + \frac{z^{3}}{3} - ... = -\sum_{n=1}^{\infty}(-1)^{n}\frac{z^{n}}{n}$ ( 对于 | z |< 1 ) 。

事实上，等式两侧微分等于 1/(1 + z )，因此，它们相差一个常量。因为两侧在 z = 0 处都等于 0 , 则这个常量一定是0 , 因此，我们已经证明了期望的 Taylor 展式。

在简单连通域中定义了一个对数之后，现在我们对于任意 α∈ℂ 定义幂 $z^{\alpha}$ 。若假设 Ω 是简单连通的且 1∈Ω 和 0 ∉ Ω ，我们选择如上具有 $\log{1}=0$ 的对数枝，并定义

$\displaystyle z^{\alpha}=e^{\alpha{\log}{z}}$ 。

注意， $1^{\alpha}=1$ ，以及若 α = 1/n，则

$\displaystyle (z^{1/n})^{n}=\prod_{k=1}^{n}e^{\frac{1}{n}\log{z}}=e^{\sum_{k=1}^{n}\frac{1}{n}\log{z}}=e^{\frac{n}{n}\log{z}}=e^{\log{z}}=z$ 。

我们知道，每一个非零复数 w 都可以写成 $w=e^{z}$ 。这个事实的一种推广在下一定理中给出，它讨论的是只要 f 不消没，则 $\log{f(z)}$ 必存在的问题。

定理 6.2 若 f 在简单连通域 Ω 中是无处消没的全纯函数，在则Ω上存在一个全纯函数 g 使得

$\displaystyle f(z)=e^{g(z)}$ 。

定理中的函数 g (z) 可以用 $\log{f(z)}$ 表示，取决于对数的“枝”。

证明：

因定 Ω 中的一定 $z_{0}$ 并定义一个函数

$\displaystyle g(z)=\int_{\gamma}\frac{f^{'}(w)}{f(w)}dw+c_{0}$ ，

其中，γ 是 Ω 中连接 $z_{0}$ 与 z 的任意路径，而 $c_{0}$ 是一个使得 $e^{c_{0}}=f(z_{0})$ 的复数。这个定义独立于路径 γ ，因为 Ω 是简单连通的。按照第2章中定理2.1的证明方法论证，可以求得 g 是全纯的，并且

$\displaystyle g^{'}(z)=\frac{f^{'}(z)}{f(z)}$ ，

通过简单计算即可给出

$\displaystyle \frac{d}{df(z)}\bigg(f(z)e^{-g(z)}\bigg) = 0$ ，

因此， $f(z)e^{-g(z)}$ 是常量。在 $z_{0}$ 点计算这个表达式，我们求得 $f(z_{0})e^{-c_{0}} = 1$ ，因此，对于任意 z∈Ω ， $f(z)=e^{g(z)}$ , 因此证明完结。

7. Fourier级数和调和函数(Fourier series and harmonic functions)

在第4章中，我们将描述复变函数理论和实数线上Fourier分析之间的一些有趣的联系。这项研究的动机部分来自于圆上的Fourier级数与圆盘中全纯函数的幂级数展开之间的简单而直接的关系，我们现在对此进行研究。

假设 f 在圆盘 $D_{R}(z_{0})$ 中是全纯的，因此 f 具有幂级数展开式

$\displaystyle f(z)=\sum_{n=0}^{\infty}a_{n}(z-z_{0})^{n}$

并且在这个圆盘上是收敛的。

定理 7.1 f 的幂级数展开式的系数由

$\displaystyle a_{n}=\frac{1}{2\pi{r^{n}}}\int_{0}^{2\pi}f(z_{0}+re^{i\theta})e^{-in\theta}d\theta$ (对于任意 n ≥0 和 0 < r < R )

给出。此外，

$\displaystyle 0=\frac{1}{2\pi{r^{n}}}\int_{0}^{2\pi}f(z_{0}+re^{i\theta})e^{-in\theta}d\theta$ (只要 n < 0 ) 。

证明：

因为 $f^{(n)}(z_{0})=a_{n}n!$ ，根据 Cauchy 积分公式得到

$\displaystyle a_{n}=\frac{1}{2\pi{i}}\int_{\gamma}\frac{f(\zeta)}{(\zeta-z_{0})^{n+1}}d\zeta$ ,

其中，γ 是中心位于 $z_{0}$ 半径为 0 < r < R 且具有正方向的圆。选择 $\zeta=z_{0}+re^{i\theta}$ 作为这个圆的参数化表达式，我们求得，对于 n ≥ 0 ,有

$\begin{array}{rlc} a_{n}&\displaystyle=\frac{1}{2\pi{i}}\int_{0}^{2\pi}\frac{f(z_{0}+re^{i\theta})}{(f(z_{0}+re^{i\theta})-z_{0})^{n+1}}d\zeta \\ \\ &\displaystyle =\frac{1}{2\pi{r}^{n}}\int_{0}^{2\pi}f(z_{0}+re^{i\theta})e^{-(n+1){\theta}}e^{i\theta}d\theta \\ \\ &\displaystyle =\frac{1}{2\pi{r}^{n}}\int_{0}^{2\pi}f(z_{0}+re^{i\theta})e^{-in{\theta}}d\theta \end{array}$ 。

最后，即使当 n < 0 时，我们的计算表明，我们仍然具有恒等式

$\displaystyle \frac{1}{2\pi{r}^{n}}\int_{0}^{2\pi}f(z_{0}+re^{i\theta})e^{-in{\theta}}d\theta =\frac{1}{2\pi{i}}\int_{\gamma}\frac{f(\zeta)}{(\zeta-z_{0})^{n+1}}d\zeta$ 。

因为 –n > 0 , 函数 $f (\zeta) (\zeta-z_{0})^{-n-1}$ 在圆盘上是全纯的，根据 Cauchy 定理，最后的积分消没。

对这个定理的解释如下：将 $f(z_{0}+re^{i\theta})$ 视为一个中心位于 $z_{0}$ 点且半径为 r 的圆盘闭包上的全纯函数的圆的限制。则其 Fourier系数在 n < 0 时消没，而当 n ≥ 0 时等于(不大于 $r^{n}$ 的一个因子)全纯函数 f 的幂级数的系数。当 n < 0 时Fourier系数消没的这个属性揭示了全纯函数的另一个专有的特殊(特别是，它们对任意圆的约束)。