关于数学中的空间之概观

ComputerInBook

已于 2025-03-10 14:04:02 修改

阅读量1k

点赞数 7

分类专栏：数学与应用数学文章标签：空间结构数学空间

于 2025-03-10 13:24:30 首次发布

本文链接：https://blog.csdn.net/ComputerInBook/article/details/146151137

版权

数学与应用数学专栏收录该内容

130 篇文章

订阅专栏

3. 数学空间的分类法(Taxonomy)

3.1 三个分类等级(Three taxonomic ranks)

3.2 空间物种间关系(Relations between species of spaces)

4. 数学空间之分类(Types of spaces)

4.1 线性空间和拓扑空间 (Linear and topological spaces)

4.2 仿射空间和射影空间 (Affine and projective spaces)

4.3 度量空间和一致空间 (Metric and uniform spaces)

4.4 赋范空间，Banach空间，内积空间，和Hilbert空间 (Normed, Banach, inner product, and Hilbert spaces)

4.5 平滑流形和Riemann流形 ( Smooth and Riemannian manifolds)

4.6 可测空间、测度空间和概率空间 (Measurable, measure, and probability spaces)

4.7 非交换几何 (Non-commutative geometry)

4.8 概形 (Schemes)

4.9 基本拓扑 (Topoi)

5. 空间和结构(Spaces and structure)

6. 空间的主要分类

1. 数学中空间的定义

在数学中，一个空间是指一个赋予了定义集合元素之间关系的结构之集合(有时称为全集(universe))(即，一个空间是指一个集合加上施加于集合之上的一种结构，这种结构定义了集合的元素之间的关系)。子空间(subspace)是保留了相同结构的父空间的子集。虽然现代数学使用多种类型的空间，例如 Euclid 空间、线性空间、拓扑空间(topological spaces)、Hilbert空间或概率空间(probability spaces)，但它并没有定义“空间”本身的概念。

一个(数学)空间由视为点的选定数学对象以及这些点之间选定的关系组成。点的性质可以千差万别：例如，点可以表示数字、另一个空间上的函数或另一个空间的子空间。关系定义了空间的性质。更准确地说，同构空间(isomorphic spaces)被认为是相同的空间，其中两个空间之间的同构是它们的点之间的一一对应关系，它们之间保留了这种关系。例如，三维 Euclid 空间的点之间的关系由Euclid公理唯一确定，并且所有三维 Euclid 空间都视为是相同的。

拓扑概念(例如连续性)对于每个Euclid空间都有自然定义。然而，拓扑不区分直线和曲线，因此Euclid空间和拓扑空间之间的关系是“易忘的”。这种关系在“空间类型”部分有更详细的讨论。

一个给定的数学对象应该被视为几何“空间”还是代数“结构”并不总是很清楚。布尔巴基(Bourbaki)提出的“结构”的一般定义涵盖了所有常见的空间类型，提供了同构的一般定义，并证明了同构结构之间属性的转移。

-------------------------------图1：一些抽象空间类型的概述。箭头表示也是一种；例如，赋范向量空间也是度量空间。--------------------------

2. 数学空间概念的发展历史

数学空间概念的发展历史表

经典	现代
公理是定义的明显含义定理是绝对的客观真理	公理是约定定理是相应公理的含义
点、线、等之间的关系是由它们的特征确定的	点、线、等之间的关系是本质的，它们之间的关系却不是
数学对象以其结构呈现给我们	每一个数学定理通过其某些属性描述其数学对象
几何对应于经验现实	几何是数学真理
空间的所有几何属性都可从公理推导	空间的公理不需要确定所有几何性质
几何学是一门自主的、活的科学	古典几何是数学的通用语言
空间是三维的	不同的维度概念适用于不同类型的空间
空间是几何的全集(universe)	空间只是数学结构，它们出现在数学的各个分支中

2.1 几何黄金时代之前的空间概念

在古希腊数学中，数学“空间”是对日常生活中观察到的三维现实的几何抽象。大约公元前 300 年，Euclid给出了空间属性的公理。Euclid在这些几何基础上建立了所有数学，甚至通过比较线段的长度和所选参考线段的长度来定义数字(注：即，一切数学对象皆几何)。

坐标法(解析几何)由René Descartes于 1637 年采用。当时，几何定理被视为可通过直觉和理性知晓的绝对客观真理，类似于自然科学的对象；而公理被视为定义的明显含义。

几何图形之间使用了两种等价关系：全等和相似。平移、旋转和反射(注：即关于某条轴对称)将图形转换为全等图形；同形体则转换为相似图形。例如，所有圆都相互相似，但椭圆并不类似于圆。第三种等价关系由Gaspard Monge于 1795 年引入，出现在射影几何(projective geometry)中：不仅椭圆，而且抛物线和双曲线在适当的射影变换下也会变成圆；它们都是射影等价图形。

Euclid几何与射影几何之间的关系表明，数学对象并不是连同其结构一起提供给我们。相反，每个数学理论都通过它们的某些属性来描述其对象，这些属性正是作为该理论基础的公理。

距离和角度不能出现在射影几何定理中，因为这些概念既不在射影几何的公理中提及，也没有从公理中提到的概念定义。“三角形三个角之和是多少”这个问题在Euclid几何中有意义，但在射影几何中却毫无意义。

19 世纪出现了不同的情况：在某些几何中，三角形三个角的总和定义明确，但与经典值(180 度)不同。 Nikolai Lobachevsky 于 1829 年和János Bolyai于 1832 年(以及Carl Friedrich Gauss于 1816 年，未发表)提出了非Euclid双曲几何，指出总和取决于三角形，并且始终小于 180 度。Eugenio Beltrami于 1868 年和Felix Klein于 1871 年获得了非Euclid双曲几何的Euclid “模型”，从而完全证明了该理论在逻辑上是可行的。

这一发现迫使人们放弃了Euclid几何的绝对真理论。它表明公理不是“显而易见的”，也不是“定义的含义”。相反，它们是假设。它们在多大程度上与实验现实相对应？这个重要的物理问题不再与数学有关。即使“几何”与实验现实不符，其定理仍然是“数学真理”。

非Euclid几何的Euclid模型是Euclid空间中存在的一些对象以及这些对象之间的一些关系的选择，这些关系满足非Euclid几何的所有公理(因此也满足所有定理)。这些Euclid对象和关系“演绎”非Euclid几何，就像当代演员演绎古代剧目一样。演员可以模仿现实中从未发生过的情况。舞台上演员之间的关系模仿了剧中角色之间的关系。同样，Euclid模型所选对象之间的所选关系模仿了非Euclid关系。它表明，数学对象之间的关系(而不是性质)在数学中至关重要。

-------图2：位似变换(homothety)通过缩放将一个几何图形转换为相似的图形。------

2.1 几何黄金时代及之后的空间概念

“几何(geometry)”一词(来自古希腊语：geo-“地球(earth)”、-metron“测量(measurement)”)最初是指处理我们所居住空间的长度、面积和体积的实用方法，但后来被广泛扩展(以及这里所讨论的空间概念)。

根据Bourbaki 1795 年(Monge的几何描述)和 1872 年(Klein的“Erlangen纲领”)之间的时期可以称为“几何的黄金时代”。Euclid最初研究的空间现在被称为三维Euclid空间。它的公理化由Euclid在 23 个世纪前开始，后来被 Hilbert 公理、Tarski公理和Birkhoff公理重新改造。这些公理系统通过受许多公理约束的原始概念(例如“点”、“之间”、“全等”)来描述空间。

解析几何取得了巨大进步，并成功地用变换群不变量的计算取代了经典几何定理。从那时起，业余爱好者对古典几何的新定理的兴趣比专业数学家更大。然而，古典几何的遗产并没有丢失。根据Bourbaki的说法，“古典几何作为一门独立而活的科学被忽视了，因此它变成了当代数学的通用语言”。

同时，数开始取代几何成为数学的基础。例如，Richard Dedekind在 1872 年的论文《连续性和非比数》(Continuity and irrational numbers)中断言，直线上的点应该具有Dedekind分割的性质，因此直线与实数集是同一事物。Dedekind谨慎地指出，这是一个无法证明的假设。在现代处理中，Dedekind的断言通常被视为直线的定义，从而将几何简化为算术。三维Euclid空间被定义为一个仿射空间，其元素差分的相关向量空间配有内积。像Euclid中的“从头开始”的定义现在不常用，因为它没有揭示这个空间与其他空间的关系。此外，三维射影空间现在定义为四维向量空间的所有一维子空间(即通过原点的直线)的空间。这种基础的转变需要一套新的公理，如果采用这些公理，几何学的经典公理就变成了定理。

现在，空间由视为点的选定数学对象(例如，另一个空间上的函数，或另一个空间的子空间，或只是一个集合的元素)以及这些点之间的选定关系组成。因此，空间只是方便的数学结构。人们可能认为被称为“空间”的结构比其他数学对象更具几何感，但这并不总是正确的。

根据Bernhard Riemann 于 1854 年发表的著名就职演讲，每个由 n 个实数参数化的数学对象都可以视为所有此类对象的 n 维空间中的一个点。当代数学家经常遵循这一思想，并发现几乎在任何地方使用古典几何术语都极具启发性。

函数是重要的数学对象。通常它们形成无限维函数空间，正如Riemann所指出并在 20 世纪通过函数分析进行了阐述的那样。

3. 数学空间的分类法(Taxonomy)

3.1 三个分类等级(Three taxonomic ranks)

虽然每种类型的空间都有自己的定义，但“空间”的一般概念却无法形式化。有些结构称为空间，而另一些则不是，没有正式的标准。此外，对“结构”的一般概念也没有达成共识。根据Pudlák的说法，“数学[...]不能完全用数学结构这样的单一概念来解释。尽管如此，Bourbaki的结构主义方法是我们所拥有的最好的方法。” 现在概述一种可能的Bourbaki精神的空间(和结构)分类。

我们将空间分为三个层次。鉴于每个数学理论都通过其对象的某些属性来描述它，首先要问的问题是：哪些属性？这导致了第一个(上层)分类级别。在第二个级别上，人们会考虑对特别重要的问题的答案(在根据第一个级别有意义的问题中)。在第三个分类级别上，人们会考虑所有可能问题的答案。

例如，上层分类区分Euclid空间和射影空间，因为两点之间的距离在Euclid空间中有定义，但在射影空间中没有定义。另一个例子。“三角形三个角的总和是多少”这个问题在Euclid空间中有意义，但在射影空间中没有意义。在非Euclid空间中，这个问题有意义，但答案不同，这不是上层区别。

此外，Euclid平面和Euclid三维空间之间的区别不是上层区别；“维度是多少”这个问题在两种情况下都有意义。

第二层分类区分Euclid空间和非Euclid空间；有限维空间和无限维空间；紧空间和非紧空间等。用Bourbaki的话来说，第二层分类是按“物种”分类。与生物分类学不同，一个空间可能属于多个物种。

例如，第三级分类区分不同维度的空间，但不区分三维Euclid空间的平面(视为二维Euclid空间)和所有实数对的集合(也视为二维Euclid空间)。同样，它也不区分同一非Euclid空间的不同Euclid模型。更正式地说，第三级将空间分类为同构。两个空间之间的同构定义为第一个空间的点与第二个空间的点之间的一一对应关系，该对应关系保留了根据第一级规定的所有关系。相互同构的空间被认为是单个空间的副本。如果其中一个属于给定的物种，那么它们都属于该物种。

同构的概念阐明了上级分类。给定同一上级类的两个空间之间的一一对应关系，人们可能会问它是否是同构。对于两个不同类别的空间来说，这个问题毫无意义。

与自身同构称为自同构。Euclid空间的自同构是这些的移位、旋转、反射和组合。Euclid空间是齐次的，因为每个点都可以通过某种自同构变换成其他每个点。

Euclid公理不留任何自由；它们唯一地确定了空间的所有几何性质。更确切地说：所有三维Euclid空间都是相互同构的。从这个意义上说，我们有“那个”三维Euclid空间。用Bourbaki的话来说，相应的理论是单价的。相反，拓扑空间通常是非同构的；它们的理论是多价的。数理逻辑中也有类似的想法：如果一个理论的所有相同基数的模型都是相互同构的，那么它就被称为范畴论的。按照Bourbaki的观点，多价理论( multivalent theories)的研究是现代数学区别于古典数学最显著的特征。

3.2 空间物种间关系(Relations between species of spaces)

拓扑概念(连续性、收敛性、开集、闭集等)在每个Euclid空间中都有自然定义。换言之，每个Euclid空间也是一个拓扑空间。两个Euclid空间之间的每个同构(isomorphism)也是相应拓扑空间之间的同构(称为“同胚(homeomorphism)”)，但反之则不正确：同胚可能会扭曲距离。用Bourbaki的话来说，“拓扑空间”是“Euclid空间”结构的底层结构。范畴论中也有类似的想法：“Euclid空间”空间范畴是拓扑空间范畴上的具体范畴；遗忘(或“剥离”)函子(functor)将前一个范畴映射到后一个范畴。

三维Euclid空间是Euclid空间的一个特例。用Bourbaki的话来说，三维Euclid空间的种类比Euclid空间的种类更丰富。同样，紧致拓扑空间的物种比拓扑空间的物种更加丰富。

空间种类之间的这种关系可以如图 3 所示以图解方式表示。从 A 到 B 的箭头表示每个 A 空间也是 B 空间，或者可以视为 B 空间，或者提供 B 空间等。将 A 和 B 视为空间类，可以将箭头解释为从 A 到 B 的过渡。(用Bourbaki的话来说，从 A 空间“推导出 B 空间。除非 A、B 类是集合，否则不完全是函数；这种细微差别不会使以下内容无效。)图 3 中的两个箭头不可逆，但原因不同。

-----------------------------------------图 3 ：空间种类之间的关系示例------------------------------------------

从“Euclid”到“拓扑”的转变是健忘的。拓扑区分连续和不连续，但不区分直线和曲线。直觉告诉我们，Euclid结构不能从拓扑中恢复。证明使用拓扑空间的自同构(即自同胚)，它不是Euclid空间的自同构(即不是移位、旋转和反射的组合)。这种变换将给定的Euclid结构变成(同构但)不同的Euclid结构；两个Euclid结构都对应于单个拓扑结构。

相反，从“三维Euclid”到“Euclid”的转变并不是健忘的；Euclid空间不一定是三维的，但如果它恰好是三维的，它就是成熟的，没有结构丢失。换句话说，后一个转换是单射(一对一)，而前一个转换不是单射(多对一)。我们用带倒钩尾部的箭头表示单射转换，“↣”而不是“→”。

这两个转换都不是满射，也就是说，不是每个 B 空间都来自某个 A 空间。首先，三维Euclid空间是Euclid空间的一个特例(不是一般情况)。其次，Euclid空间的拓扑是拓扑的一个特例(例如，它必须是非紧致的、连通的等)。我们用双头箭头表示满射转换，“↠”而不是“→”。例如，参见图 4；在那里，从“实线性拓扑”到“实线性”的箭头是双头的，因为每个实线性空间都允许某种(至少一个)与其线性结构兼容的拓扑。

这种拓扑一般不唯一，但当实线性空间是有限维时，它是唯一的。对于这些空间，转换既是单射又是满射，即双射；参见图 4 中从“有限维实线性拓扑”到“有限维实线性”的箭头。逆转换存在(可以用第二个向后的箭头表示)。因此，这两种结构是等价的。在实践中，人们不会区分等价的结构。等价结构可以视为单个结构，如图 4 中的大框所示。

箭头表示的转换遵循同构。也就是说，两个同构的 A 空间导致两个同构的 B 空间。

图 4 上的图是交换的。也就是说，图中所有具有相同起点和终点的有向路径都导致相同的结果。下面的其它图表也是可交换的，除了图 9 中的虚线箭头。从“拓扑”到“可测”的箭头是虚线，原因在那里解释道：“为了将拓扑空间变成可测空间，需要赋予它一个 σ代数。Borel 集的 σ代数是最受欢迎的，但不是唯一的选择。”实线箭头表示一种普遍的所谓“规范”转换，这种转换自然而然地出现，并且被广泛使用，通常是默认的隐式转换。例如，在谈论Euclid空间上的连续函数时，不需要明确指定其拓扑。事实上，存在替代拓扑，有时会使用，例如精细拓扑；但这些拓扑总是明确指定的，因为它们比普遍的拓扑不那么引人注目。虚线箭头表示正在使用几种转换，但没有一种转换非常普遍。

-----------------------------------------图 4 ：数学空间之间的关系：线性、拓扑等---------------------------

4. 数学空间之分类(Types of spaces)

4.1 线性空间和拓扑空间 (Linear and topological spaces)

线性空间(也称为向量空间)和拓扑空间是两个基本空间。

线性空间具有代数性质；有实线性空间(在实数域上)、复线性空间(在复数域上)，更一般地，有任意域上的线性空间。每个复线性空间也是实线性空间(后者是前者的基础)，因为每个复数都可以用两个实数指定。例如，作为一维复线性空间处理的复平面可以降级为二维实线性空间。相反，实线可以被视为一维实线性空间，但不能被视为复线性空间。另请参阅域扩展。更一般地，域上的向量空间也具有该域子域上的向量空间的结构。根据定义，在线性空间中给出的线性运算导致诸如直线(和平面以及其他线性子空间)、平行线、椭圆(和椭圆体)等概念。但是，不可能定义正交(垂直)线，也不可能在椭圆中单独挑出圆，因为在线性空间中没有像标量积这样的结构可用于测量角度。线性空间的维数定义为线性独立向量的最大数量，或者等价地，定义为张成的空间的向量的最小数量；它可以是有限的，也可以是无限的。同一域上的两个线性空间当且仅当它们具有相同的维数时才是同构的。n 维复线性空间也是 2n 维实线性空间。

拓扑空间具有解析性质。根据定义，在拓扑空间中给出的开集导致诸如连续函数、路径、映射；收敛序列、极限；内部、边界、外部等概念。但是，一致连续性、有界集、Cauchy序列、可微函数(路径、映射)仍未定义。拓扑空间之间的同构传统上称为同胚；这些是双向连续的一一对应。开区间 (0,1) 同胚于整个实线 (−∞,∞)，但不同胚于闭区间 [0,1]，也不同胚于圆。立方体的表面同胚于球体(球的表面)，但不同胚于圆环。不同维度的Euclid空间不是同胚的，这似乎很明显，但不容易证明。拓扑空间的维度很难定义；可以使用归纳维度(基于几何图形边界的维度通常比图形本身的维度小一的观察)和Lebesgue覆盖维度。在 n 维 Euclid 空间的情况下，两个拓扑维度都等于 n。

拓扑空间的每个子集本身都是拓扑空间(相反，只有线性空间的线性子集才是线性空间)。任意拓扑空间，由一般拓扑学(也称为点集拓扑学)研究，过于多样化，无法完全分类到同胚。紧拓扑空间是拓扑空间的重要一类(此“类型”的“种类”)。每个连续函数都在这样的空间上有界。闭区间 [0,1] 和扩展实线 [−∞,∞] 是紧的；开区间 (0,1) 和线 (−∞,∞) 不是。几何拓扑研究流形(此“类型”的另一个“种类”)；这些是局部同胚于Euclid空间的拓扑空间(并满足一些额外条件)。低维流形完全分类到同胚。

线性和拓扑结构都是线性拓扑空间(换言之，拓扑向量空间)结构的基础。线性拓扑空间既是实数或复数线性空间，又是拓扑空间，因此线性运算是连续的。因此，具有拓扑结构的线性空间通常不是线性拓扑空间。

每个有限维实线性空间或复线性空间都是线性拓扑空间，因为它具有一个且只有一个拓扑，使其成为线性拓扑空间。因此，“有限维实线性空间或复线性空间”和“有限维线性拓扑空间”这两个结构是等价的，即相互基础。因此，有限维线性拓扑空间的每个可逆线性变换都是同胚。三种维度概念(一个代数维度和两个拓扑维度)对于有限维实线性空间是一致的。然而，在无限维空间中，不同的拓扑可以符合给定的线性结构，并且可逆线性变换通常不是同胚。

4.2 仿射空间和射影空间 (Affine and projective spaces)

通过线性空间引入仿射空间和射影空间很方便，如下所示。(n + 1) 维线性空间的 n 维线性子空间本身也是 n 维线性空间，因此不是齐次的(homogeneous)；它包含一个特殊点，即原点。将其移位一个外部向量，可获得 n 维仿射子空间。它是齐次的。仿射空间不必包含在线性空间中，但与线性空间的仿射子空间同构。给定域上的所有 n 维仿射空间都是相互同构的。用 John Baez 的话来说，“仿射空间是忘记了其起源的向量空间”。特别是，每个线性空间也是仿射空间。

给定 (n + 1) 维线性空间 L 中的 n 维仿射子空间 A，A 中的直线可以定义为 A 与 L 中与 A 相交的二维线性子空间的交点：换句话说，与通过原点但不平行于 A 的平面的交点。更一般地，A 的 k 维仿射子空间是 A 与 L 中与 A 相交的 (k + 1) 维线性子空间的交点。

仿射子空间 A 的每个点都是 A 与 L 的一维线性子空间的交点。但是，L 的一些一维子空间与 A 平行；在某种意义上，它们在无穷远处与 A 相交。( n + 1) 维线性空间的所有一维线性子空间的集合根据定义是 n 维射影空间。并且仿射子空间 A 作为真子集嵌入到射影空间中。但是，射影空间本身是齐次的。射影空间中的直线对应于 (n + 1) 维线性空间的二维线性子空间。更一般地，射影空间的 k 维射影子空间对应于 ( n + 1) 维线性空间的 (k + 1) 维线性子空间，并且与 k 维射影空间同构。

按照这种方式定义，仿射空间和射影空间具有代数性质；它们可以是实数、复数，更一般地，可以是任何域上的。

每个实数或复数仿射空间或射影空间也是拓扑空间。仿射空间是非紧流形；射影空间是紧流形。在实射影空间中，直线与圆同胚，因此是紧的，与仿射空间的线性直线相反。

-------------------------------图 5：数学空间之间的关系：仿射、射影等-----------------------------------------

4.3 度量空间和一致空间 (Metric and uniform spaces)

点之间的距离在度量空间中定义。度量空间之间的同构称为等距(isometries)。每个度量空间也是一个拓扑空间。如果拓扑空间位于度量空间之下，则称为可度量的(metrizable)。所有流形都是可度量的。

在度量空间中，我们可以定义有界集和Cauchy序列。如果所有Cauchy序列都收敛，则度量空间称为完整的(complete)。每个非完备空间都作为稠密子集等距嵌入到完全空间 (完备空间)(completion)。每个紧度量空间都是完备的；实线是非紧的但完备的；开区间 (0,1) 是不完备的。

每个Euclid空间也是完备度量空间。此外，Euclid空间中固有的所有几何概念都可以用其度量来表征。例如，连接两个给定点 A 和 C 的直线段由所有点 B 组成，使得 A 和 C 之间的距离等于两个距离( A 和 B 之间以及 B 和 C 之间的距离)之和。

Hausdoff维数(与覆盖给定集合的小球数量有关)适用于度量空间，并且可以是非整数(尤其是对于分形)。对于n 维Euclid空间，Hausdoff 维数等于 n。

一致(或均匀)空间不引入距离，但仍允许使用一致连续性、Cauchy序列(或滤子或网格)、完整性(completeness)或完备性(completion)。每个一致空间也是拓扑空间。每个线性拓扑空间(无论是否可度量化)也是一致空间，并且在有限维上是完备的，但在无限维上通常是不完备的。更一般地，每个交换拓扑群也是一致空间。然而，非交换拓扑群带有两个一致结构，一个是左不变的，另一个是右不变的。

----------------------------------图 6：数学空间之间的关系：度量、一致等-----------------------------------

4.4 赋范空间，Banach空间，内积空间，和Hilbert空间 (Normed, Banach, inner product, and Hilbert spaces)

Euclid空间中的向量构成线性空间，但每个向量x 也具有长度，即范数 ‖x‖(注：所谓范数就是度量向量的长度，“范”即“度量”)。赋予范数的实数或复数线性空间是赋范空间。每个赋范空间既是线性拓扑空间，又是度量空间。Banach 空间是完备赋范空间。许多序列或函数空间都是无限维 Banach 空间。

所有范数小于 1 的向量之集合称为有范数空间的单位球。它是一个凸的、中心对称的集合，通常不是椭圆体；例如，它可以是一个多边形(在平面上)，或者更一般地，是一个多面体(在任意有限维中)。平行四边形定律(也称为平行四边形恒等式)

$\displaystyle \lVert {x-y} \rVert^{2} +\lVert {x+y} \rVert^{2} = 2\lVert {x} \rVert^{2} + 2\lVert {y} \rVert^{2}$

通常在赋范空间中失效，但对Euclid空间中的向量成立，这是因为向量的Euclid范数平方是其自身的内积，即 $\lVert {x} \rVert ^{2}=(x,x)$ 。

内积空间是实数或复数线性空间，具有双线性或半线性形式，满足某些条件，称为内积。每个内积空间也是赋范空间。赋范空间是内积空间的基础，当且仅当它满足平行四边形定律，或者等效地，当其单位球是椭圆体时。向量之间的角度在内积空间中定义。Hilbert空间被定义为完备内积空间。(一些作者坚持认为它必须是复数，其他人也承认实数Hilbert空间。) 许多序列或函数空间都是无限维Hilbert空间。Hilbert空间对量子理论非常重要。

所有 n 维实数内积空间都是相互同构的。可以说 n 维Euclid空间是忘记了起源的 n 维实数内积空间。

--------------------------图 7：数学空间之间的关系：赋范空间、Banach空间等-----------------------------

4.5 平滑流形和Riemann流形 ( Smooth and Riemannian manifolds)

平滑流形不称为“空间(spaces)”，但可以当成空间。每个平滑流形都是拓扑流形，并且可以嵌入有限维线性空间。有限维线性空间中的光滑表面是平滑流形：例如，椭圆体的表面是平滑流形，而多面体不是。实数或复数有限维线性、仿射和射影空间也是平滑流形。

在其每个点处，平滑流形中的平滑路径都有一个切向量，该切向量属于该点处流形的切空间。n 维平滑流形的切空间是 n 维线性空间。平滑函数在平滑流形上的微分在每个点处提供切空间上的线性函数。

Riemann流形或Riemann空间是一种平滑流形，其切空间具有满足某些条件的内积。Euclid空间也是Riemann空间。Euclid空间中的平滑表面是Riemann空间。双曲非Euclid空间也是Riemann空间。Riemann空间中的曲线具有长度，两点之间最短曲线的长度定义了距离，因此Riemann空间是度量空间。两条曲线在一点相交的夹角是它们切线之间的夹角。

放弃切空间内积的正性，可以得到伪Riemann空间，包括对广义相对论非常重要的 Lorentz空间。

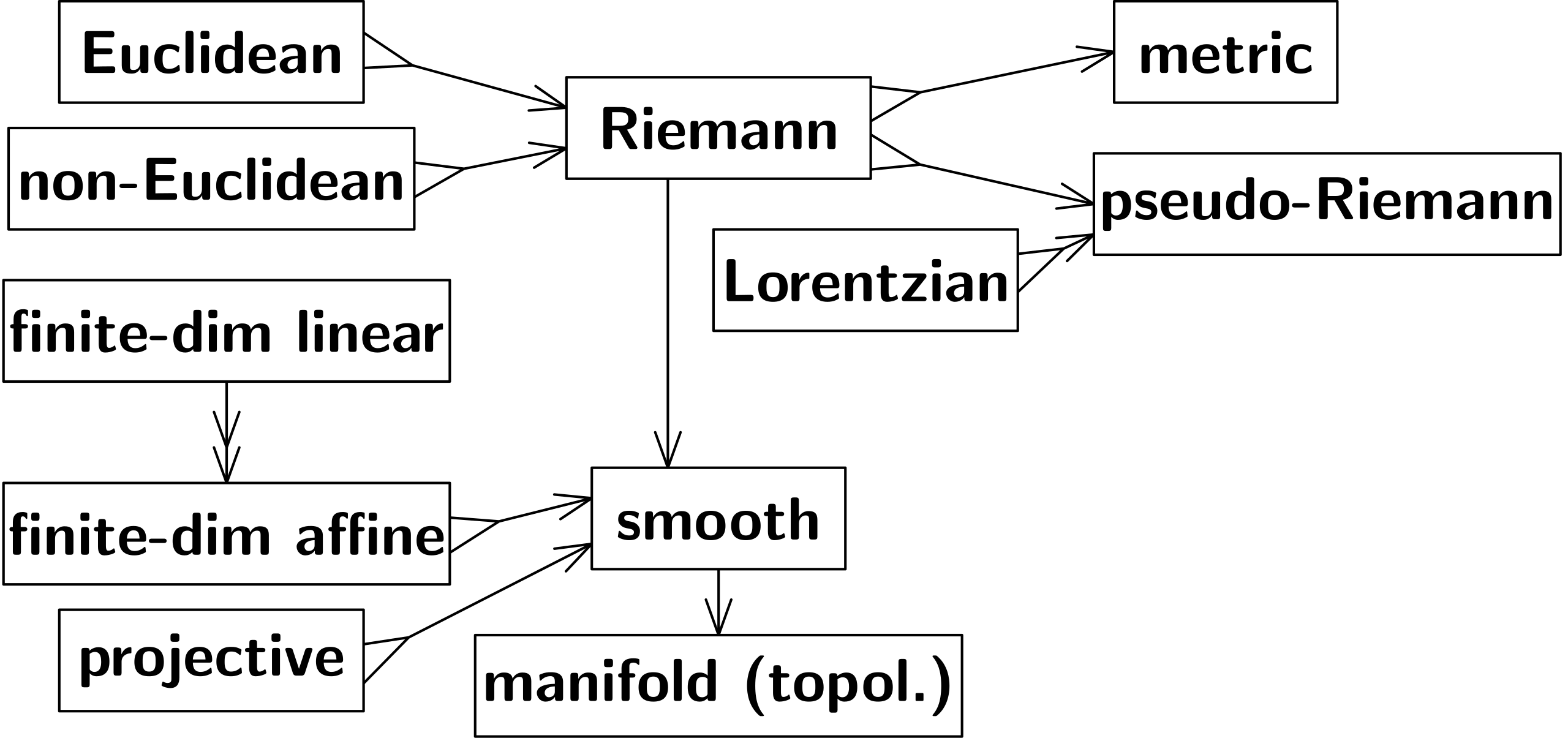
--------------------------图 8：数学空间之间的关系：平滑空间、Riemann空间等-------------------------

4.6 可测空间、测度空间和概率空间 (Measurable, measure, and probability spaces)

放弃距离和角度，同时保留体积(几何体)，就得到了测度论。除了体积之外，根据Andrey Kolmogorov的概率论方法，测度还概括了面积、长度、质量(或电荷)分布以及概率分布的概念。

古典数学中的“几何体”比一组点更为规则。几何体的边界体积为零。因此，几何体的体积是其内部的体积，内部可以通过无限的立方体序列穷竭。相反，任意点集的边界可以是非零体积(例如：给定立方体内所有比率点的集合)。测度论成功地将体积概念扩展到一大类集合，即所谓的可测集。事实上，不可测集几乎从未出现在应用中。

根据定义，在可测空间中给出的可测集导出了可测函数和映射。为了将拓扑空间变成可测空间，需要为其赋予一个 σ代数。Borel 集的 σ 代数是最受欢迎的，但并非唯一选择。(有时也会使用Baire集、普遍可测集(Universally measurable set)等)拓扑并非由 Borel σ代数唯一确定；例如，可分离Hilbert空间上的范数拓扑和弱拓扑导致相同的 Borel σ代数。并非每个 σ代数都是某个拓扑的 Borel σ代数。实际上，σ代数可以由给定的集合(或函数)集合生成，与任何拓扑无关。可测空间的每个子集本身也是可测空间。

标准可测空间(也称为标准 Borel 空间)特别有用，因为它与紧致空间有相似之处(参见 EoM)。标准可测空间之间的每个双射可测映射都是同构的；也就是说，逆映射也是可测的。并且，当且仅当其图在乘积空间中可测时，此类空间之间的映射才是可测的。同样，紧致度量空间之间的每个双射连续映射都是同构的；也就是说，逆映射也是连续的。并且，当且仅当其图在乘积空间中封闭时，此类空间之间的映射才是连续的。

Euclid空间(更一般地，在完全可分度量空间中)中的每个 Borel 集，如果赋予 Borel σ代数，都是标准可测空间。所有不可数标准可测空间都是相互同构的。

测度空间是赋予了测度的可测空间。具有Lebesgue测度的Euclid空间是测度空间。积分理论定义了测度空间上可测函数的可积性和积分。

测度为 0 的集合称为零集(null sets)，可忽略不计。因此，“模 0 同构”定义为全测度子集(即具有可忽略的补集)之间的同构。

概率空间是整个空间的测度等于 1 的测度空间。任何概率空间族(有限或非有限)的乘积都是概率空间。相反，对于一般的测度空间，只定义有限多个空间的乘积。因此，有许多无限维概率测度(尤其是Gauss测度)，但没有无限维Lebesgue测度。

标准概率空间特别有用。在标准概率空间上，条件期望可以视为条件测度的积分(常规条件概率，另见测度分解)。给定两个标准概率空间，它们的测度代数的每个同态都由某个测度保持映射诱导。标准可测空间上的每个概率测度都会产生标准概率空间。标准概率空间序列(有限或有限)的乘积是标准概率空间。所有非原子(no-atomic)标准概率空间都是模 0 相互同构的；其中一个是具有Lebesgue测度的区间 (0,1)。

这些空间的几何性较差。特别是，维度的概念(以某种形式)适用于所有其他空间，但不适用于可测空间、测度空间和概率空间。

--------------------------------图 9：数学空间之间的关系：可测空间、测度空间等------------------------

4.7 非交换几何 (Non-commutative geometry)

微积分的理论研究，即数学分析，在 20 世纪早期引发了对实值或复值函数线性空间的思考。这些空间最早的例子是函数空间，每个函数空间都适用于自己的一类问题。这些空间具有许多共同的特征，这些特征很快被抽象为Hilbert空间、Banach空间和更一般的拓扑向量空间。这些空间是解决各种数学问题的强大工具包。

最详细的信息由一类称为Banach代数的空间提供。这些是Banach空间与连续乘法运算的结合。一个重要的早期例子是测度空间 X 上本质上有界可测函数的Banach代数。这组函数是逐点加法和标量乘法下的Banach空间。通过逐点乘法运算，它成为一种特殊的Banach空间，现在称为交换von Neumann代数。逐点乘法确定了该代数在 X 上平方可积函数的Hilbert空间上的表示。John von Neumann早期的观察是，这种对应关系反过来也成立：给定一些温和的技术假设，交换的von Neumann代数与Hilbert空间上的表示一起确定了测度空间，并且这两个构造(von Neumann代数加表示和测度空间)互为逆。

von Neumann随后提出，非交换的von Neumann代数应该具有几何意义，就像交换的von Neumann代数一样。他与Francis Murray一起对von Neumann代数进行了分类。直接积分构造显示了如何将任何von Neumann代数分解为一组称为因子的更简单的代数。von Neumann和Murray将因子分为三类。类型 I 与交换的情况几乎相同。类型 II 和 III 表现出新的现象。 II 型von Neumann代数确定了一种几何，其特点是维度可以是任何非负实数，而不仅仅是整数。III 型代数既不是 I 型也不是 II 型代数，经过几十年的努力，它们被证明与 II 型因子密切相关。

与 von Neumann 和 Murray 对因子分类的研究同时，还发展了一种略有不同的函数空间几何方法。这种方法是 $C^{*}$ 代数理论，这里，激励的例子是 $C^{*}$ 代数 $C_{0}(x)$ ，其中，X是局部紧致 Hausdorff 拓扑空间。根据定义，这是 X 上连续复函数的代数，这些函数在无穷远处消没(大致意味着，距离选定点越远，函数越接近于零)，具有逐点加法和乘法运算。 Gelfand-Naimark 定理暗示交换 $C^{*}$ 代数与几何对象之间存在对应关系：对于某个局部紧致的 Hausdorff 空间 X，每个交换 $C^{*}$ 代数的形式为 $C_{0}(x)$ 。因此，可以纯粹根据交换 $C^{*}$ 代数来研究局部紧致的 Hausdorff 空间。非交换几何以此为灵感，研究非交换 $C^{*}$ 代数：如果存在“非交换空间 X ”这样的东西，那么它的 $C_{0}(x)$ 将是非交换 $C^{*}$ 代数；如果将 Gelfand-Naimark 定理应用于这些不存在的对象，那么空间(无论是否交换)都将与 $C^{*}$ 代数相同；因此，由于缺乏对非交换空间定义的直接方法，非交换空间被定义为非交换代数。许多标准几何工具可以用 $C^{*}$ 代数重新表述，这为研究非交换 $C^{*}$ 代数提供了几何启发的技术。

这两个例子现在都是非交换几何领域的案例。von Neumann代数和 $C^{*}$ 代数的具体例子分别称为非交换测度理论和非交换拓扑。非交换几何不仅仅是为了追求普遍性，也不仅仅是一种好奇心。非交换空间自然而然地，甚至是不可避免地从某些构造中产生。例如，考虑由风筝和飞镖组成的非周期性彭罗斯平面平铺。有一条定理，在这样的平铺中，每个有限的风筝和飞镖斑块都会无限次出现。因此，无法通过查看有限部分来区分两个Penrose平铺。这使得不可能以传统意义上为所有平铺的集合分配拓扑。尽管如此，彭罗斯拼贴确定了一个非交换的 $C^{*}$ 代数，因此可以用非交换几何技术来研究它们。另一个例子，也是微分几何中一个非常有趣的例子，来自流形的叶子层。这些是将流形分成称为叶子的较小维度子流形的方法，每个叶子都与附近的其他叶子局部平行。所有叶子的集合可以组成一个拓扑空间。然而，无理旋转的例子表明，这种拓扑空间无法用经典测度论的技术来访问。然而，有一个非交换的von Neumann代数与叶子层的叶子空间相关联，这再次为原本难以理解的空间提供了良好的几何结构。

4.8 概形 (Schemes)

代数几何研究多项式方程的几何性质。多项式是一种由加法和乘法的基本算术运算定义的函数。因此，它们与代数密切相关。代数几何提供了一种将几何技术应用于纯代数问题的方法，反之亦然。(注：似乎说成几何代数更贴切。)

20 世纪 40 年代之前，代数几何专门研究复数，最基本的簇是射影空间(projective space)。射影空间的几何与透视理论(perspective)密切相关，其代数由齐次多项式描述。所有其他簇都被定义为射影空间的子集。射影簇是由一组齐次多项式定义的子集。在射影簇的每个点，集合中的所有多项式都必须等于零。线性多项式零集的补集是仿射空间(affine space)，仿射簇是射影簇与仿射空间的交集。

André Weil发现几何推理有时可以应用于数论情况，其中所讨论的空间可能是离散的甚至是有限的。为了追求这个想法，Weil重写了代数几何的基础，既将代数几何从对复数的依赖中解放出来，又引入了不嵌入射影空间的抽象代数簇。这些现在被简称为簇。

大多数现代代数几何的基础空间类型比Weil的抽象代数簇更为通用。它由Alexander Grothendieck (亚历山大·格罗滕迪克)引入，称为概形(scheme)。方案理论的动机之一是多项式在函数中的结构异常，因此代数簇(algebraic varieties)是刚性的(rigid)。这在尝试研究退化情况时会带来问题。例如，圆上几乎任何一对点都会确定一条称为割线的唯一线，并且当这两个点绕圆移动时，割线会不断变化。然而，当两点相碰时，割线退化为切线。切线是唯一的，但这种配置的几何形状(圆上的单个点)不足以表达出一条唯一的线。研究这种情况需要一种能够为退化情况分配额外数据的理论。

概形的构建块之一是拓扑空间。拓扑空间具有连续函数，但连续函数过于一般，无法反映感兴趣的底层代数结构。因此，概形中的另一个要素是拓扑空间上的层，称为“结构层(structure sheaf )”。在拓扑空间的每个开子集上，层指定一组函数，称为“正则函数(regular functions)”。拓扑空间和结构层一起要求满足意味着函数来自代数运算的条件。

与流形一样，概形定义为在熟悉空间上局部建模的空间。在流形的情况下，熟悉的空间是Euclid空间。对于概形，局部模型称为仿射方案。仿射方案提供了代数几何和交换代数之间的直接联系。交换代数的基本研究对象是交换环。如果 R 是交换环，则存在相应的仿射概形 $\mathbf{Spec}{\;R}$ 的代数结构转换为几何结构。相反，每个仿射概形都会确定一个交换环，即其结构层的全局部分环。这两个操作互为逆运算，因此仿射概形提供了一种研究交换代数问题的新语言。根据定义，概形中的每个点都有一个开邻域，这是一个仿射概形。

有许多概形不是仿射的。特别是，射影空间满足称为适当性的条件，该条件类似于紧致性。仿射概形不可能是适当的(除了在概形只有一个点等简单情况下)，因此没有射影空间是仿射概形(零维射影空间除外)。射影概形(即射影空间的闭子概形)是最重要的一类概形。

已经引入了几种概形的概括。Michael Artin 将代数空间定义为概形除以定义 Étale 态射(Étale morphism)的等价关系的商。代数空间保留了概形的许多有用属性，同时更加灵活。例如，Keel-Mori 定理可用于证明许多模空间是代数空间。

比代数空间更通用的是 Deligne-Mumford(DM) 栈。DM 栈类似于概形，但它们允许不能仅用多项式描述的奇点。它们对概形的作用与 orbifold 对流形的作用相同。例如，仿射平面除以围绕原点的有限旋转群的商产生 Deligne-Mumford 栈，它不是概形或代数空间。远离原点，群作用的商确定了圆上等距点的有限集。但在原点处，圆仅由一个点组成，即原点本身，群作用固定了这一点。然而，在商 DM 栈中，这个点带有作为商的额外数据。这种精炼结构在模空间理论中很有用，事实上，它最初是为描述代数曲线的模而引入的。

进一步的概括是代数栈，也称为 Artin 栈。DM 栈仅限于有限群作用的商。虽然这足以解决模理论中的许多问题，但对于其他问题来说太过严格，而 Artin 栈允许更一般的商。

------------------------------------------图 10：数学空间之间的关系：概形、栈等---------------------------

4.9 基本拓扑 (Topoi)

在Grothendieck关于Weil猜想的研究中，他引入了一种新型拓扑，现在称为Grothendieck拓扑。拓扑空间(在普通意义上)公理化了“接近(nearness)”的概念，使两个点在且仅当它们位于许多相同的开集中时才接近。相比之下，Grothendieck拓扑公理化了“覆盖(covering)”的概念。空间的覆盖是子空间的集合，它们共同包含周围空间的所有信息。由于层(sheaves)是根据覆盖定义的，因此Grothendieck拓扑也可以看作是层理论的公理化。

Grothendieck在拓扑方面的工作使他获得了拓扑理论。在他的回忆录《收获与播种》中(Récoltes et Semailles)，他称其为“最广阔的概念(most vast conception)”。层(无论是在拓扑空间上还是相对于Grothendieck拓扑)用于表达局部数据。所有层的范畴包含表达局部数据的所有可能方式。由于拓扑空间是由点构成的，而点本身就是一种局部数据，因此层范畴可以用作原始空间的替代。因此，Grothendieck将拓扑定义为层范畴，并将拓扑作为其本身感兴趣的对象进行研究。这些现在被称为Grothendieck拓扑。

每个拓扑空间都确定一个拓扑，反之亦然。有些拓扑空间采用相关拓扑会丢失信息，但这些通常被认为是病态的(pathological)。(必要和充分条件是——拓扑空间是一个Sober空间(Sober space))相反，有些拓扑的相关拓扑空间不会体现原始拓扑。但是，这些拓扑远非病态，而是具有极大的数学意义。例如，Grothendieck的抽象上同调理论(最终导致了Weil猜想的证明)可以表述为一个概形的抽象拓扑中的上同调，而这个拓扑不是来自拓扑空间。

事实上，拓扑空间会产生非常特殊的拓扑，称为局部。拓扑空间的开子集之族合决定了晶格(lattice)。拓扑空间的公理使这些晶格成为完整的 Heyting 代数。局部理论以此为起点。局部被定义为完整的 Heyting 代数，拓扑空间的基本性质用这些术语重新表达和重新证明。局部的概念比拓扑空间更通用，因为每个朴素的拓扑空间都决定了一个唯一的局部，但许多有趣的局部并非来自拓扑空间。由于局部不需要有点，因此局部的研究被戏称为无意义拓扑。

拓扑还与数理逻辑有着深刻的联系。每个 Grothendieck 拓扑都有一个特殊的层，称为子对象分类器。这个子对象分类器的功能类似于所有可能真值的集合。在集合拓扑中，子对象分类器是集合{0 , 1}，对应于“假(False)”和“真(True)”。但在其他拓扑中，子对象分类器可能要复杂得多。Lawvere 和 Tierney 认识到，公理化子对象分类器产生了一种更通用的拓扑，现在称为基本拓扑，而基本拓扑是直觉逻辑的模型。除了提供一种将逻辑工具应用于几何的强大方法之外，这还使得在逻辑中使用几何方法成为可能。

----------------------------------图 11：数学空间之间的关系：局部、基本拓扑等-------------------------------

5. 空间和结构(Spaces and structure)

根据 Kevin Arlin 的说法，

[ 这两个词 [“空间(space)”和“结构(space)”] 都没有一个数学定义。这两个英文单词基本上可以在所有相同的情况下使用，但你经常认为“空间”更几何，而“结构”更代数。[...] 所以你可以把“结构”看作我们做代数的地方，把“空间”看作我们做几何的地方。然后，许多伟大的数学都来自于从结构到空间的转变，反之亦然，就像我们看拓扑空间的基本群或环的谱(spectrum)时一样。但最终，这种区别既不严格也不固定，而且只到此为止：许多东西显然既是结构又是空间，有些东西也不明显，有些人可能会不同意我在这里所说的一切。]

尽管如此，Bourbaki提出了“结构”的一般定义；它涵盖了上面提到的所有类型的空间，(几乎？)迄今为止使用的所有类型的数学结构，等等。它提供了同构的一般定义，并证明了同构结构之间的性质转移。然而，它从未在数学实践中被积极使用(甚至在Bourbaki自己写的数学论文中也没有)。以下是Robert Reed ]对Leo Corry所著书籍的评论的最后几句话：

“Corry 似乎并不认为任何正式的结构定义能够公正地对待这个概念在实际数学实践中的使用[...] Corry 的观点可以概括为这样的信念：“结构”本质上是指一种做数学的方式，因此是一个无法与数学本身的文化产物一样精确定义的概念。”

几何“空间”和代数“结构”之间的区别有时很明显，有时很难捉摸。显然，群是代数的，而Euclid空间是几何的。环上的模和群一样是代数的。特别是，当环看起来是一个域时，模看起来是一个线性空间；它是代数的还是几何的？特别是，当它是有限维的、在实数上，并赋予内积时，它就变成了Euclid空间；现在是几何的。实数的(代数？)域与(几何？)实线相同。它的代数闭包，即复数的(代数？)域，与(几何？)复平面相同。它首先是“我们进行分析的地方”(而不是代数或几何)。

上文“空间类型”部分中讨论的每个空间(除“非交换几何”、“概形”和“拓扑”子部分外)都是一个集合(根据Bourbaki的说法，是结构的“主基集(principal base set)”)，并赋予了一些附加结构；基集的元素通常称为该空间的“点”。相反，代数结构(基集)的元素通常不称为“点”。

但是，有时会使用多个主基集。例如，二维射影几何可以通过两个基集(点集和线集)形式化。此外，射影平面的一个显著特征是点和线所起的作用是对称的。一个不太几何的例子：一个图可以通过两个基集形式化，即顶点集(也称为节点或点)和边集(也称为弧或线)。通常，Bourbaki规定了有限多个主基集和有限多个辅助基集。

上文“非交换几何”、“概形”和“拓扑”小节中讨论的许多几何数学结构都没有规定基点集。例如，“无点拓扑”(换句话说，无点拓扑或局部理论)以单个基集开始，其元素模仿拓扑空间中的开集(但不是点集)；另请参阅部分拓扑和无点几何。