You are given a table consisting of n rows and m columns. Each cell of the table contains a number, 0 or 1. In one move we can choose some row of the table and cyclically shift its values either one cell to the left, or one cell to the right.
To cyclically shift a table row one cell to the right means to move the value of each cell, except for the last one, to the right neighboring cell, and to move the value of the last cell to the first cell. A cyclical shift of a row to the left is performed similarly, but in the other direction. For example, if we cyclically shift a row "00110" one cell to the right, we get a row "00011", but if we shift a row "00110" one cell to the left, we get a row "01100".
Determine the minimum number of moves needed to make some table column consist only of numbers 1.
The first line contains two space-separated integers: n (1 ≤ n ≤ 100) — the number of rows in the table and m (1 ≤ m ≤ 104) — the number of columns in the table. Then n lines follow, each of them contains m characters "0" or "1": the j-th character of the i-th line describes the contents of the cell in the i-th row and in the j-th column of the table.
It is guaranteed that the description of the table contains no other characters besides "0" and "1".
Print a single number: the minimum number of moves needed to get only numbers 1 in some column of the table. If this is impossible, print -1.
3 6 101010 000100 100000
3
2 3 111 000
-1
In the first sample one way to achieve the goal with the least number of moves is as follows: cyclically shift the second row to the right once, then shift the third row to the left twice. Then the table column before the last one will contain only 1s.
In the second sample one can't shift the rows to get a column containing only 1s.
题意:
给出一个n和一个m，接下来给出n行01字符串，每串长度为m，可以将每一行进行左移或者右移(例如 00011 左移为00110 右移为10001)，需要将每一行进行多少次左移右移的操作，才能得到一列全1的情况，如果不管怎么移动，都得不到一列为全1，就输出-1，否则输出最少移动次数。
题解:
首先，我们得先得到每一行的1的个数和他们所在的下标。以方便我们以当前枚举位置为标记，二分出一个离它左边最近的一个1(当然，当前位置也有可能是不存在离它最近的一个1的)。
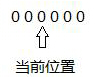
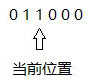
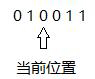
全0 只有左边有1 当前位置为1 左右两边都有1 只有右边有1
首先这个过程中，排除一行全为0的情况，这种情况，就不能构成其中一列为1，所以-1的的情况，也只存在这个。
为什么要枚举离当前位置左边最近的一个1呢。
当然，当前位置如果如果本身就是1的话，那么这一行不需要移动，这列就能得到一个1了，就可以直接不移动。
但是如果当前位置为0，那么我们就需要通过左移右移来得到一个1来使得该行该列为1。
那么我们二分出来的结果(离当前位置的左边最近的一个1)
如果存在这个结果，那么就分开两种情况
①是如果当前结果已经是该行下标最大的一个1了
那么比较的就是min( 当前位置 - 结果位置 , ( m - 1 ) - 当前位置 + ( 最左边一个1的位置 + 1 ) )
最左边一个1的位置 就是当前行保存的1的数组的第一个
②并不是下标最大的一个1，就说明在当前位置的右边，还有1的存在
那么比较的就是min( 当前位置 - 结果位置 , (结果下标+1的位置) - 当前位置 )
因为我们二分返回结果，设为返回我得到的该结果的下标，那么下标+1就是它的下一项，即离当前位置右边最近的一个。
如果不存在这个结果
那么就代表1都在当前位置的右边
那么比较的就是min( 1的下标数组的第一个 - 当前位置 , ( m - 1 ) + ( 当前位置 + 1 ) - ( 1的下标数组的最后一个))
然后得到比较一个每一列的转变次数，得到最小即可。
因为一开始写循环是用从每一行开始，再判断每一列的，所以多开了个数组来记录每一列等达成全1需要的步数。
#pragma comment(linker, "/STACK:102400000,102400000")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
using namespace std;
typedef long long ll;
const int N=1e2+5;
const int M=1e4+5;
const int INF=0x3f3f3f3f;
char Map[N][M];
struct node
{
int pos[M];
int cnt;
}num[N];
int res[M];
int binarysearch(int key,int id,int l,int r)//得到最右边一个<=key
{
while (l<=r)
{
int mid=l+((r-l)>>1);
if (num[id].pos[mid]<=key)
l=mid+1;
else
r=mid-1;
}
if (r>=0)
return r;
return -1;
}
int main()
{
int n,m;
while (~scanf("%d%d",&n,&m))
{
bool flag=0;
memset(res,0,sizeof(res));
for (int i=0 ; i<n ; ++i)
{
scanf("%s",Map[i]);
bool fl=0;
num[i].cnt=0;
for (int j=0 ; j<m ; ++j)
{
if (Map[i][j]=='1')
{
fl=1;
num[i].pos[num[i].cnt++]=j;
}
}
if (!fl)//有一行不存在1的情况,那么就无法构成一列为全1的情况
flag=1;
}
if (flag)
{
printf("-1\n");
continue;
}
for (int i=0 ; i<n ; ++i)
{
for (int j=0 ; j<m ; ++j)
{
if (Map[i][j]=='1')//当前位置为1 不需要移动
continue;
int now=binarysearch(j,i,0,num[i].cnt-1);
int r=0;
if (now==num[i].cnt-1 && now!=-1)//1全部都在当前位置的左边
r=min(j-num[i].pos[now],(m-1)-j+(num[i].pos[0]+1));
else if (now!=-1 && now<num[i].cnt-1)//左右两边都有1,判断最近是哪个
r=min(j-num[i].pos[now],num[i].pos[now+1]-j);
else//1全部都在当前位置的右边
r=min(num[i].pos[0]-j,(m-1)-num[i].pos[num[i].cnt-1]+(j+1));
res[j]+=r;
}
}
int ans=INF;
for (int i=0 ; i<m ; ++i)
ans=min(res[i],ans);
printf("%d\n",ans);
}
return 0;
}
实际上可以简化成从每一列开始，记录当前列需要的步数，然后比较出最小值，就能得到答案了。
#pragma comment(linker, "/STACK:102400000,102400000")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
using namespace std;
typedef long long ll;
const int N=1e2+5;
const int M=1e4+5;
const int INF=0x3f3f3f3f;
char Map[N][M];
struct node
{
int pos[M];
int cnt;
}num[N];
int binarysearch(int key,int id,int l,int r)
{
while (l<=r)
{
int mid=l+((r-l)>>1);
if (num[id].pos[mid]<=key)
l=mid+1;
else
r=mid-1;
}
if (r>=0)
return r;
return -1;
}
int main()
{
int n,m;
while (~scanf("%d%d",&n,&m))
{
bool flag=0;
for (int i=0 ; i<n ; ++i)
{
scanf("%s",Map[i]);
bool fl=0;
num[i].cnt=0;
for (int j=0 ; j<m ; ++j)
{
if (Map[i][j]=='1')
{
fl=1;
num[i].pos[num[i].cnt++]=j;
}
}
if (!fl)
flag=1;
}
if (flag)
{
printf("-1\n");
continue;
}
int ans=INF;
for (int j=0 ; j<m ; ++j)
{
int cnt=0;
for (int i=0 ; i<n ; ++i)
{
if (Map[i][j]=='1')
continue;
int now=binarysearch(j,i,0,num[i].cnt-1);
int r=0;
if (now==num[i].cnt-1 && now!=-1)
r=min(j-num[i].pos[now],(m-1)-j+(num[i].pos[0]+1));
else if (now!=-1 && now+1<num[i].cnt)
r=min(j-num[i].pos[now],num[i].pos[now+1]-j);
else
r=min(num[i].pos[0]-j,(m-1)-num[i].pos[num[i].cnt-1]+(j+1));
cnt+=r;
}
ans=min(ans,cnt);
}
printf("%d\n",ans);
}
return 0;
}
扫一扫
297
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
