题意:
给出一个x,问至多用3个素数,以乘法和加法组合起来,能有多少种方法得到x。
因为不会使用括号,所以只有 a、a+b、a*b、a+b+c、a*b+c、a*b*c
题解:
首先,根据题意,只有小于等于80000的全部素数才能构成结果,那么我们只需要先打表出这个素数表。
打表的过程中,我们就可以先处理出结果本身就是素数和当前素数*3得到的值(即a+a+a三个相同的素数相加)的方案数+1。
ans[i]=ans[i]+1 ans[i*3]=ans[i*3]+1;
先说带有乘法或者只有乘法的方案数计算。
①a*b
直接暴力枚举 1到cnt(小于等于80000的素数的个数) 内的素数相乘,枚举的b必须大于或者等于a,避免重复计数,并且必须保证a*b不大于80000。因为a*b不能大于80000,那么我们枚举过程中,将a的范围缩小为不超过sqrt(80000)。
ans[a*b]=ans[a*b]+1
②a*b+c
根据上面的枚举结果,得到所有的a*b的结果,列为多项式,跟另外一个多项式(所有小于等于80000的素数)做一次多项式相乘,得到a*b+c的所有结果,再保存到ans[i]里面。
ans[i]=ans[i]+res[i] res[i]为当前多项式计算结果
③a*b*c
直接暴力枚举符合情况,枚举过程中,b不能小于a,c不能小于b即可,就能得到所有结果。
ans[a*b*c]=ans[a*b*c]+1
再说只有加法的方案数计算
①a+b
这个只要直接用小于等于80000的素数的多项式相互相乘,去掉不同的两个数相加的时候的重复计算就可以得到最后的答案。
ans[i]=ans[i]+res[i] res[i]为当前多项式计算结果
②a+b+c
这个的去重,就比较麻烦了。单独从a+b来说,我们只需要去掉因为顺序不同的重复计算,即使 2+3、3+2这样的情况。
a+b+c如果 a、b、c取值都不一样的话,那么会有三种情况 a+b+c、a+c+b、b+c+a 要得到结果我们只需要将这个方案数/3即可
而 2+2+3、2+3+2这样的情况就比较尴尬了,其中有两个数是相等的情况下,最终结果只会出现2次,那么如果是上述那样方案数/3会使得结果变少。
为了解决这个问题,我们直接去掉a+b结果中的相同的结果(即a==b的情况),才进行第二个加法的多项式相乘,得到的结果只会出现2+3+2。
为了弥补缺失的方案数,我们再做一次 2*a 跟 素数的多项式相乘的结果,我们可以得到所有的a+a+b的结果,而且只有一次,那么我们只要*2加上上面原来出现的一次,就达到三次了。
而三个数相等的计算,一开始我们就说了。所以这种情况的最后结果是
ans[i]=ans[i]+(res[i]+tmp[i]*2)/3 res[i]为三种取值不同和第一次加法时去掉相同的数相加的情况 tmp为2*a+b的结果
#pragma comment(linker, "/STACK:102400000,102400000")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
using namespace std;
typedef long long ll;
const double PI=acos(-1.0);
const int N=8e4+5;
const int M=1<<18;
const int mod=1e9+7;
bool mark[N];
int prim[N];
int cnt;
ll ans[N],res[M],tmp[M];
struct Complex
{
double real,image;
Complex(double r=0.0,double i=0.0):real(r),image(i){}
Complex operator + (const Complex &b)
{
return Complex(real+b.real,image+b.image);
}
Complex operator - (const Complex &b)
{
return Complex (real-b.real,image-b.image);
}
Complex operator * (const Complex &b)
{
return Complex (real*b.real-image*b.image,image*b.real+real*b.image);
}
}a[M],b[M];
void change(Complex x[],int len)
{
for (int i=1,j=len/2 ; i<len-1 ; ++i)
{
if (i<j)
swap(x[i],x[j]);
int k=len/2;
while (j>=k)
{
j-=k;
k/=2;
}
if (j<k)
j+=k;
}
}
void FFT(Complex x[],int len,int dft)
{
change(x,len);
for (int h=2 ; h<=len ; h<<=1)
{
Complex wn(cos(2*PI*dft/h),sin(2*PI*dft/h));
for (int j=0 ; j<len ; j+=h)
{
Complex w(1,0);
for (int k=j ; k<j+h/2 ; ++k)
{
Complex u=x[k];
Complex t=w*x[k+h/2];
x[k]=u+t;
x[k+h/2]=u-t;
w=w*wn;
}
}
}
if (dft==-1)
{
for (int i=0 ; i<len ; ++i)
{
x[i].real/=len;
x[i].image/=len;
}
}
}
void twomuladd(int len)//两个相乘之后加一个数的情况
{
memset(res,0,sizeof(res));
for (int i=0 ; i<cnt && prim[i]<=sqrt(N) ; ++i)//两个数相乘等于x
{
for (int j=i ; j<cnt ; ++j)
{
if ((ll)prim[i]*prim[j]>=(ll)N)
break;
res[prim[i]*prim[j]]++;
ans[prim[i]*prim[j]]=(ans[prim[i]*prim[j]]+1)%mod;
}
}
for (int i=0 ; i<len ; ++i)
{
if (i<N)
{
a[i]=Complex(res[i],0);
b[i]=Complex(!mark[i],0);
}
else
a[i]=b[i]=Complex(0,0);
}
FFT(a,len,1);
FFT(b,len,1);
for (int i=0 ; i<len ; ++i)
a[i]=a[i]*b[i];
FFT(a,len,-1);
for (int i=0 ; i<len ; ++i)
res[i]=(ll)(a[i].real+0.5);
for (int i=0 ; i<N ; ++i)
ans[i]=(ans[i]+res[i]%mod)%mod;
}
void threeadd(int len)//两个相加跟三个相加的情况(不包括三个相同的相加)
{
for (int i=0 ; i<len ; ++i)
{
if (i<N)
a[i]=b[i]=Complex(!mark[i],0);
else
a[i]=b[i]=Complex(0,0);
}
FFT(a,len,1);
for (int i=0 ; i<len ; ++i)
a[i]=a[i]*a[i];
FFT(a,len,-1);
for (int i=0 ; i<len ; ++i)//;两个相加
{
res[i]=(ll)(a[i].real+0.5);
res[i]=res[i]&1?(res[i]+1)/2:res[i]/2;//去掉两个相加的时候的重复计算
}
for (int i=0 ; i<N ; ++i)
ans[i]=(ans[i]+res[i]%mod)%mod;
for (int i=0 ; i<len ; ++i)
res[i]=(ll)(a[i].real+0.5);
for (int i=0 ; i<cnt ; ++i)//去掉自身相加的结果
res[prim[i]+prim[i]]--;
for (int i=0 ; i<len ; ++i)//去掉两个相加的时候的重复计算
res[i]/=2;
for (int i=0 ; i<len ; ++i)
{
if (i<N)
a[i]=Complex(res[i],0);
else
a[i]=Complex(0,0);
}
FFT(a,len,1);
FFT(b,len,1);
for (int i=0 ; i<len ; ++i)//三个相加
a[i]=a[i]*b[i];
FFT(a,len,-1);
for (int i=0 ; i<len ; ++i)
res[i]=(ll)(a[i].real+0.5);
for (int i=0 ; i<len ; ++i)
{
if (i<N)
a[i]=Complex(!mark[i],0);
else
a[i]=Complex(0,0);
b[i]=Complex(0,0);
}
for (int i=0 ; i<cnt ; ++i)
if (prim[i]*2<N)
b[prim[i]*2]=Complex(1,0);
FFT(a,len,1);
FFT(b,len,1);
for (int i=0 ; i<len ; ++i)//两个重复的加上另外一个数
a[i]=a[i]*b[i];
FFT(a,len,-1);
for (int i=0 ; i<len ; ++i)
tmp[i]=(ll)(a[i].real+0.5);
for (int i=0 ; i<len ; ++i)
res[i]=(res[i]+tmp[i]*2)/3;
for (int i=0 ; i<N ; ++i)
ans[i]=(ans[i]+res[i]%mod)%mod;
}
void threemul()//三个相乘的情况
{
for (int i=0 ; i<cnt ; ++i)
{
bool flag=0;
for (int j=i ; j<cnt ; ++j)
{
if ((ll)prim[i]*prim[j]>(ll)N)
break;
for (int k=j ; k<cnt ; ++k)
{
if (i==j && k==j && (ll)prim[i]*prim[j]*prim[k]>(ll)N)
{
flag=1;
break;
}
if ((ll)prim[i]*prim[j]*prim[k]>N)
break;
ans[prim[i]*prim[j]*prim[k]]=(ans[prim[i]*prim[j]*prim[k]]+1)%mod;
}
if ((ll)prim[i]*prim[j]*prim[j]>=(ll)N || flag)
break;
}
if (flag)
break;
}
}
void initial()
{
cnt=0;
mark[0]=mark[1]=1;
memset(ans,0,sizeof(ans));
for (int i=2 ; i<N ; ++i)
{
if (!mark[i])
{
prim[cnt++]=i;
ans[i]=(ans[i]+1)%mod;//当前数为素数(即用一个数)
if (i*3<N)
ans[i*3]=(ans[i*3]+1)%mod;//三个相同的数相加
}
for (int j=0 ; j<cnt && i*prim[j]<N ; ++j)
{
mark[i*prim[j]]=1;
if (!(i%prim[j]))
break;
}
}
int len=1;
while (len<(N<<1))
len<<=1;
twomuladd(len);
threeadd(len);
threemul();
}
int main()
{
initial();
int x;
while (~scanf("%d",&x))
{
printf("%lld\n",ans[x]);
}
return 0;
}







 本文探讨了K-Goldbach问题,即通过至多三个素数的加法和乘法组合来表示一个整数x的方法数量。文章详细介绍了如何通过预处理素数表并运用多项式相乘等技巧高效解决该问题。
本文探讨了K-Goldbach问题,即通过至多三个素数的加法和乘法组合来表示一个整数x的方法数量。文章详细介绍了如何通过预处理素数表并运用多项式相乘等技巧高效解决该问题。





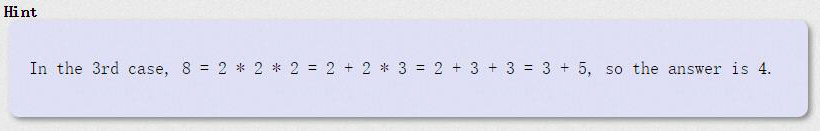
















 1872
1872

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








