题意:
给出一个T,代表T组数据。接下来每组数据含有一个n和m,表示这个序列有n个数,这n个数的和是m。再接下来给出m+1个数,表示这n个数任意组合(不重复组合)得到的和的方案数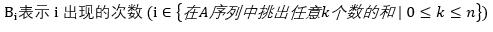
题解:
虽然我知道DP能写的很简短。
因为平常不搞DP,所以对DP并不敏感,这个题第一反应给我的是母函数(然而平常也很少写了,并没有调出一个更优的板子,所以在比赛过程中一直在TLE)。
母函数的想法其实跟原题解的想法是一致的,我们根据前面得到的A的一些数,来得到后面的组合方案,去掉这些方案后,看看是否为0,如果不为0,证明这个数也是符合A序列的,加到答案当中。
因为原本的题面是说A序列中,是非负数,那么肯定认为有0的情况存在,所以我代码中,先剔除了0的影响,而只因0而构成的方案数(不包括空集的时候),应该是B[0]-1的,为了剔除这个影响,所有B[i]都除去B[0],这样可以保证不受0的任何影响,当然,貌似最终题面改了,不存在0的情况,所以可以不作这个处理。
根据自己的观察,我们可以很容易发现,除了B[0]为1,从0开始到下一位不为0的情况,我们设为first,我们可以很容易得到B[first]
就是第1到第B[first]位的A的序列,因为不存在任何数能构成first,除了他们自身,因为他们是最小的,那么首先我们就可以得到第一个多项式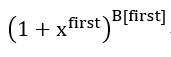
那么接下来,我们就能往后面,减去当前得到的A序列中的小数组合对后面的数的组合的影响,当B[i]的方案数,大于我当前多项式中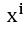
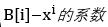
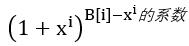
然而,正常的母函数的板子,复杂度实在是太高了,而我们的多项式中,又有很多个0,其实那些项都是多余的,根本不需要去作处理,那么我们就可以保存下当前多项式非0位的位置,然后再做母函数的组合,我们就能很大的降低了复杂度。最后经过这样的处理之后,我们就不会超时啦。
#pragma comment(linker, "/STACK:102400000,102400000")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
using namespace std;
typedef long long ll;
const int N=1e4+10;
int B[N];
int c1[N],c2[N],c3[N];
int h1[N],h2[N],h3[N];
int ans[N];
int l1,l2,l3;
int n,m;
int main()
{
int T;
scanf("%d",&T);
while (T--)
{
scanf("%d%d",&n,&m);
for (int i=0 ; i<=m ; ++i)
scanf("%d",&B[i]);
int cnt=0;
if (B[0]>1)
for (int i=0 ; i<B[0]-1 ; ++i)
ans[cnt++]=0;
for (int i=0 ; i<=m ; ++i)
B[i]/=B[0];
int fi=1;
for (int i=1 ; i<=m ; ++i)
{
if (B[i])
{
fi=i;
break;
}
}
for (int i=0 ; i<B[fi]-B[0]+1 ; ++i)
ans[cnt++]=fi;
if (cnt>=n)
{
for (int i=0 ; i<n ; ++i)
{
if (i)
printf(" ");
printf("%d",ans[i]);
}
printf("\n");
continue;
}
for (int i=0 ; i<=m ; ++i)
c1[i]=c2[i]=c3[i]=0;
l1=0;
int now=1;
int up=B[fi],down=1;
for (int i=0 ; i<=B[fi] ; ++i)
{
c1[h1[l1++]=i*fi]=now;
now*=up;
now/=down;
up-=1;
down+=1;
}
for (int i=fi+1 ; i<=m ; ++i)
{
if (B[i] && c1[i]<B[i])
{
for (int j=0 ; j<B[i]-c1[i] ; ++j)
ans[cnt++]=i;
if (cnt>=n)
break;
now=1;
up=B[i]-c1[i];
down=1;
l3=0;
l2=0;
for (int j=0 ; j<=B[i]-c1[i] ; ++j)
{
c3[h3[l3++]=j*i]=now;
now*=up;
now/=down;
up-=1;
down+=1;
}
for (int j=0 ; j<l1 ; ++j)
{
for (int k=0 ; k<l3 ; ++k)
{
if (!c2[h1[j]+h3[k]])
h2[l2++]=h1[j]+h3[k];
c2[h1[j]+h3[k]]+=c1[h1[j]]*c3[h3[k]];
}
}
for (int j=0 ; j<l2 ; ++j)
{
c1[h2[j]]=c2[h2[j]];
h1[j]=h2[j];
c2[h2[j]]=c3[h3[j]]=0;
}
l1=l2;
}
}
for (int i=0 ; i<n ; ++i)
{
if (i)
printf(" ");
printf("%d",ans[i]);
}
printf("\n");
}
return 0;
}






























 142
142

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








