UVA 1151 && POJ 2784 - Buy or Build 最小生成树 二进制枚举

Buy or Build

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 1497		Accepted: 575

Description

World Wide Networks (WWN) is a leading company that operates large telecommunication networks. WWN would like to setup a new network in Borduria, a nice country that recently managed to get rid of its military dictator Kurvi-Tasch and which is now seeking for investments of international companies (for a complete description of Borduria, have a look to the following Tintin albums ``King Ottokar's Sceptre", ``The Calculus Affair" and ``Tintin and the Picaros"). You are requested to help WWN todecide how to setup its network for a minimal total cost. 
Problem 
There are several local companies running small networks (called subnetworks in the following) that partially cover the n largest cities of Borduria. WWN would like to setup a network that connects all n cities. To achieve this, it can either build edges between cities from scratch or it can buy one or several subnetworks from local companies. You are requested to help WWN to decide how to setup its network for a minimal total cost. 

• All n cities are located by their two-dimensional Cartesian coordinates. 
  
• There are q existing subnetworks. If q>=1 then each subnetwork c ( 1<=c<=q ) is defined by a set of interconnected cities (the exact shape of a subnetwork is not relevant to our problem). 
  
• A subnetwork c can be bought for a total cost wc and it cannot be split (i.e., the network cannot be fractioned). 
  
• To connect two cities that are not connected through the subnetworks bought, WWN has to build an edge whose cost is exactly the square of the Euclidean distance between the cities.

You have to decide which existing networks you buy and which edges you setup so that the total cost is minimal. Note that the number of existing networks is always very small (typically smaller than 8). 
A 115 Cities Instance 
Consider a 115 cities instance of the problem with 4 subnetworks (the 4 first graphs in Figure 1). As mentioned earlier the exact shape of a subnetwork is not relevant still, to keep figures easy to read, we have assumed an arbitrary tree like structure for each subnetworks. The bottom network in Figure 1 corresponds to the solution in which the first and the third networks have been bought. Thin edges correspond to edges build from scratch while thick edges are those from one of the initial networks. 

Input

The first line contains the number n of cities in the country ( 1<=n<=1000 ) followed by the number q of existing subnetworks ( 0<=q<=8 ). Cities are identified by a unique integer value ranging from 1 to n . The first line is followed by q lines (one per subnetwork), all of them following the same pattern: The first integer is the number of cities in the subnetwork. The second integer is the the cost of the subnetwork (not greater than 2 x 10 ⁶ ). The remaining integers on the line (as many as the number of cities in the subnetwork) are the identifiers of the cities in the subnetwork. The last part of the file contains n lines that provide the coordinates of the cities (city 1 on the first line, city 2 on the second one, etc). Each line is made of 2 integer values (ranging from 0 to 3000) corresponding to the integer coordinates of the city.

Output

Your program has to write the optimal total cost to interconnect all cities.

Sample Input

7 3
2 4 1 2
3 3 3 6 7
3 9 2 4 5
0 2
4 0
2 0
4 2
1 3
0 5
4 4

Sample Output

17

Hint

Sample Explanation: The above instance is shown in Figure 2. An optimal solution is described in Figure 3 (thick edges come from an existing network while thin edges have been setup from scratch). 


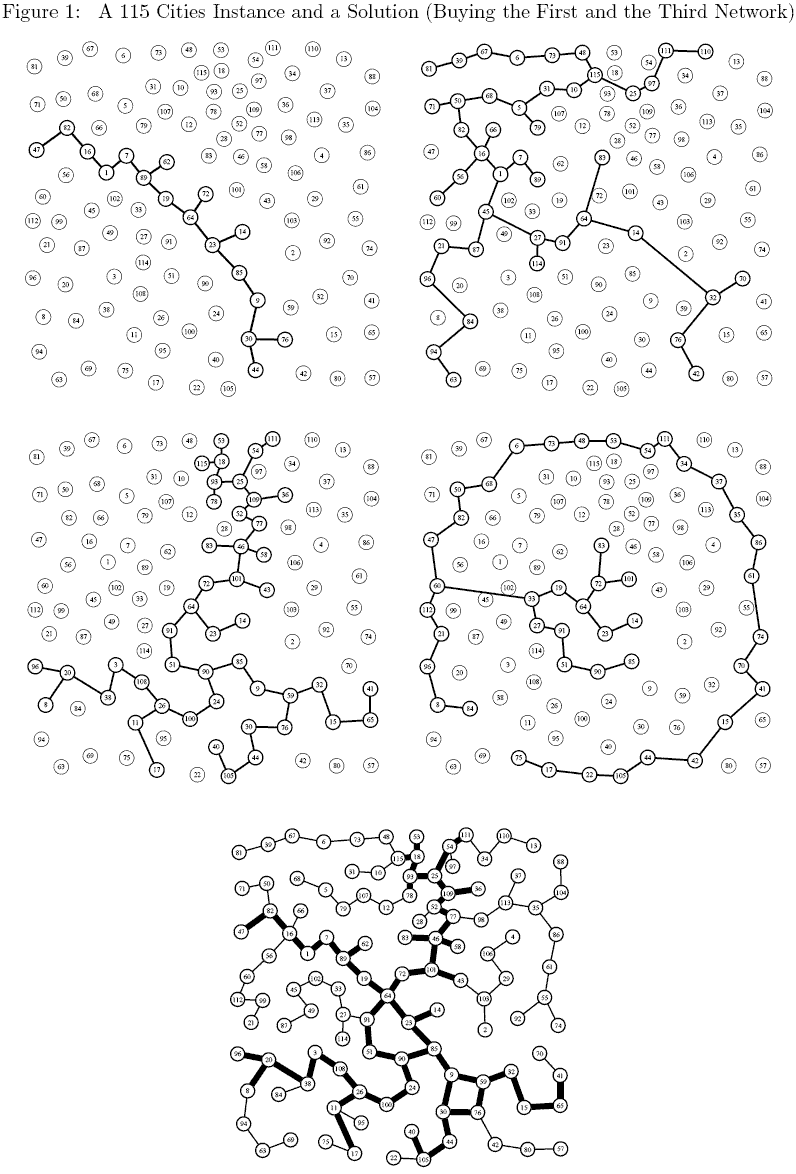
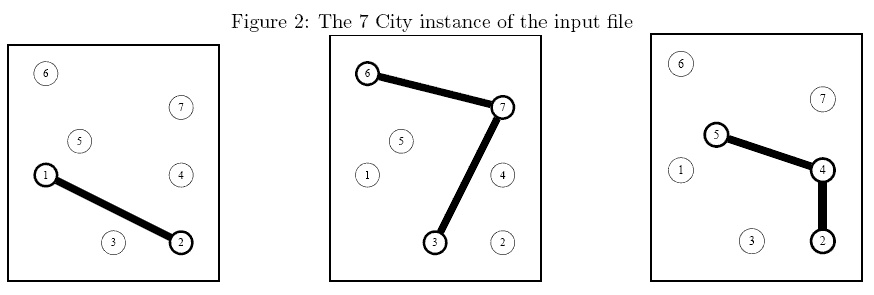
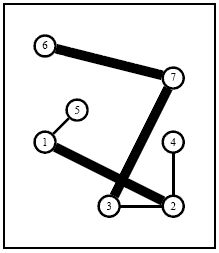
Figure 3: An optimal solution of the 7 City instance in which which the first and second existing networkshave been bought while two extra edges (1, 5) and (2, 4) 

Source

Southwestern Europe 2005

题意：建一棵树可通过购买若干个子网（子网中的点都是相互连通的），也可以自己建边。问最小的费用是多少。

思路：可以枚举每一种方案，然后在建树。简化的思路是，先建树，这样剩下的边就会很少，然后枚举每一种方案。枚举的方法用二进制枚举。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <climits> ///需要添加该头文件，否则INT_MAX不会通过
#include <vector>
using namespace std;
const int MAX_V = 1005;
const int MAX_E = 500500;
const int INF = INT_MAX;

int V, E = 0, Q, num = 0;
int par[MAX_V];
int ran[MAX_V];
int cost[10];
vector<int> g[10];

struct vertex {
    int x;
    int y;
};

vertex ve[MAX_V];

void init(int n)
{
    for(int i = 0; i < n; ++i) {
        par[i] = i;
        ran[i] = 0;
    }
}

int fin(int x)
{
    if(par[x] == x) {
        return x;
    } else {
        return par[x] = fin(par[x]);
    }
}

bool same(int x, int y)
{
    return fin(x) == fin(y);
}

void unite(int x, int y)
{
    x = fin(x);
    y = fin(y);
    if(x == y) {
        return ;
    }
    if(ran[x] < ran[y]) {
        par[x] = y;
    } else {
        par[y] = x;
        if(ran[x] == ran[y]) {
            ran[x]++;
        }
    }
}

struct edge {
    int u, v, cost;
};

bool comp(const edge & e1, const edge & e2)
{
    return e1.cost < e2.cost;
}

edge es[MAX_E];   //原来的边
edge es2[MAX_V];  //最小生成树的边

void kruskal()
{
    init(V);
    sort(es, es + E, comp);
    for(int k = 0; k < E; ++k) {
        edge e = es[k];
        if(!same(e.u, e.v)) {
            unite(e.u, e.v);
            es2[num++] = e;
        }
    }
}

int kruskal2()
{
    int sum = 0;
    for(int k = 0; k < V - 1; ++k) {
        edge e = es2[k];
        if(!same(e.u, e.v)) {
            unite(e.u, e.v);
            sum += e.cost;
            //cout << "u:" << e.u << "   v:" << e.v << "   cost: " << e.cost << endl;
        }
    }
    return sum;
}

int solve()
{
    kruskal();
    sort(es2, es2 + V - 1, comp);
    int ans = INF;
    for(int i = 0; i < (1 << Q); ++i) {  //枚举每一种方案
        init(V);
        int all = 0;
        for(int j = 0; j < Q; ++j) {
            if(!((i >> j) & 1)) {
                continue;
            }
            all += cost[j];
            for(int k = 1; k < g[j].size(); ++k) {   //一种方案中的点相当于已经在一个集合内了
                unite(g[j][k], g[j][0]);
            }
        }
        ans = min(ans, (kruskal2() + all));
    }
    return ans;
}


int main()
{
    int T;
    scanf("%d", &T);
    while(T--) {
        num = 0, E = 0;
        scanf("%d%d", &V, &Q);
        for(int i = 0; i < Q; ++i) {
            g[i].clear();
            int temp;
            scanf("%d%d", &temp, &cost[i]);
            for(int j = 0; j < temp; ++j) {
                int temp2;
                scanf("%d", &temp2);
                temp2--;
                g[i].push_back(temp2);
            }
        }
        for(int i = 0; i < V; ++i) {
            scanf("%d%d", &ve[i].x, &ve[i].y);
        }
        for(int i = 0; i < V; ++i) {
            for(int j = i + 1; j < V; ++j) {        //计算初始的边
                es[E].v = i;
                es[E].u = j;
                es[E].cost = (ve[i].x - ve[j].x) * (ve[i].x - ve[j].x) + (ve[i].y - ve[j].y) * (ve[i].y - ve[j].y);
                E++;
            }
        }
        printf("%d\n", solve());
        if(T != 0) puts("");
    }
    return 0;
}