A-题目描述:第几天
2000年的1月1日,是那一年的第1天
那么,2000年的5月4日,是那一年的第几天?
答案:
125
我的思路:
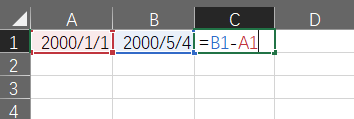
用Excel 左边和右边分别写日期,在第三个直接相减,得结果↓
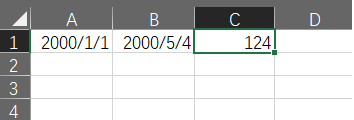
再加 1 等于125(至于为什么加 1 ,可以想想本日期减本日期等于 0 )
B-题目描述:明码
汉字的字形存在于字库中,即便在今天,16点阵的字库也仍然使用广泛。
16点阵的字库把每个汉字看成是16x16个像素信息。并把这些信息记录在字节中。
一个字节可以存储8位信息,用32个字节就可以存一个汉字的字形了。
把每个字节转为2进制表示,1表示墨迹,0表示底色。每行2个字节,
一共16行,布局是:
第1字节,第2字节
第3字节,第4字节
....
第31字节, 第32字节
这道题目是给你一段多个汉字组成的信息,每个汉字用32个字节表示,这里给出了字节作为有符号整数的值。
题目的要求隐藏在这些信息中。你的任务是复原这些汉字的字形,从中看出题目的要求,并根据要求填写答案。
这段信息是(一共10个汉字):
4 0 4 0 4 0 4 32 -1 -16 4 32 4 32 4 32 4 32 4 32 8 32 8 32 16 34 16 34 32 30 -64 0
16 64 16 64 34 68 127 126 66 -124 67 4 66 4 66 -124 126 100 66 36 66 4 66 4 66 4 126 4 66 40 0 16
4 0 4 0 4 0 4 32 -1 -16 4 32 4 32 4 32 4 32 4 32 8 32 8 32 16 34 16 34 32 30 -64 0
0 -128 64 -128 48 -128 17 8 1 -4 2 8 8 80 16 64 32 64 -32 64 32 -96 32 -96 33 16 34 8 36 14 40 4
4 0 3 0 1 0 0 4 -1 -2 4 0 4 16 7 -8 4 16 4 16 4 16 8 16 8 16 16 16 32 -96 64 64
16 64 20 72 62 -4 73 32 5 16 1 0 63 -8 1 0 -1 -2 0 64 0 80 63 -8 8 64 4 64 1 64 0 -128
0 16 63 -8 1 0 1 0 1 0 1 4 -1 -2 1 0 1 0 1 0 1 0 1 0 1 0 1 0 5 0 2 0
2 0 2 0 7 -16 8 32 24 64 37 -128 2 -128 12 -128 113 -4 2 8 12 16 18 32 33 -64 1 0 14 0 112 0
1 0 1 0 1 0 9 32 9 16 17 12 17 4 33 16 65 16 1 32 1 64 0 -128 1 0 2 0 12 0 112 0
0 0 0 0 7 -16 24 24 48 12 56 12 0 56 0 -32 0 -64 0 -128 0 0 0 0 1 -128 3 -64 1 -128 0 0
答案:
387420489
我的思路:
大致明白题目的含义,我先按照把给的数字以2、2、2…的行字节数向下排,每16行间加多个换行符,直到排完,每行的数字再转换成二进制的形式(负数则加补码),以 0 是空字符、 1 是 * 字符的形式打印
我的编程:
#include<iostream>
#include <cstdlib>
using namespace std;
int a[320];
int b[320];
void isitoa(int a)
{
static int j = 0;
itoa(a[2*k],b[j],2);
j++;
itoa(a[2*k+1],b[j],2);
}
int main()
{
for (int i = 0;i<320;i++)
{
cin>>a[i];
}
for(int j = 0;j<16;j++)
{
for(int k = 0;k<160;k++)
{
isitoa(a[2*k]);
isitoa(a[2*k+1]);
cout<<b[j]<<" "<<b[j-1];
cout<<"\n";
}
cout<<"\n\n\n";
}
return 0;
}
我这个编程很有问题,首先是[Error] ‘k’ was not declared in this scope,即在isitoa()函数中没有定义 k 的值,我已经不知道要把 k 定义在哪里了(定义在for循环外面,函数个两层循环会无法运行,又不可能定义在里面,这样for循环无法运行),就算我把这个问题解决了,又不清楚isitoa()函数是否是这样操作的(我连它是否真实存在于C函数库都不知道),就算我还是解决了,甚者我都不知道这个isitoa()函数是不是能转换负数,最后我还没有把 0 和 1 的转换写出来(果然编程真的是有思路没算法是活不了的)…
别人的编程:
#include<iostream>
using namespace std;
int a[456];
void print(int x)
{
if(x< 0) x+= 256;//取补码
for(int i = 7;i>= 0;i--)
{
if(x&(1<<i)) putchar('*');
else putchar(' ');
}
}
int main()
{
int cnt = 1;
while(cnt<= 320&&cin>>a[cnt]) cnt++;
for(int i = 1;i< cnt;i++)
{
print(a[i]);
if(i%2 == 0)printf("\n");
if(i%32 == 0) printf("\n\n\n");
}
return 0;
}
简洁又清晰
别人的思路:
每行两个字节,负数用补码,取反加一,打印出来即可(九的九次方)
我学到的:
可以用 if 判断的就尽量不要用 for 循环
比如 if ( i % 2 == 0)可以用这种表达式判断是否换行
其中 if (x & (1 << i) ) putchar( ’ * ’ ) 这一表达式不仅包含了十进制转换二进制,还包含了打印 * 号(若是 1 )具体原理如下↓
for(int i = 7;i>= 0;i--) 列出八种情况
{
if(x&(1<<i)) putchar('*'); 每种情况的判断
else putchar(' ');
}
1 << i 意思是将 1 的二进制向做移 i 格; & 意思是当两个相应位都为1,则该位的结果为1,否则为0
以第一层循环为例(x 取 5):
左边是:0000 0101
右边是:1000 0000
x&(1<<i)的结果就是: 0000 0000, 故 if 条件不成立,打印空字符
以第六层循环为例(x 取 5):
左边是:0000 0101
右边是:0000 0100
x&(1<<i)的结果就是: 0000 0100, 故 if 条件成立,打印 * 号
八层循环下来就是:空空空空空 * 空 *
C-题目描述:乘积尾零
如下的10行数据,每行有10个整数,请你求出它们的乘积的末尾有多少个零?
5650 4542 3554 473 946 4114 3871 9073 90 4329
2758 7949 6113 5659 5245 7432 3051 4434 6704 3594
9937 1173 6866 3397 4759 7557 3070 2287 1453 9899
1486 5722 3135 1170 4014 5510 5120 729 2880 9019
2049 698 4582 4346 4427 646 9742 7340 1230 7683
5693 7015 6887 7381 4172 4341 2909 2027 7355 5649
6701 6645 1671 5978 2704 9926 295 3125 3878 6785
2066 4247 4800 1578 6652 4616 1113 6205 3264 2915
3966 5291 2904 1285 2193 1428 2265 8730 9436 7074
689 5510 8243 6114 337 4096 8199 7313 3685 211
注意:需要提交的是一个整数,表示末尾零的个数。不要填写任何多余内容
答案:
31
我的思路:
第二次做,发现其实都用不到结构体(不知道以前在搞什么),只要把题意理解了就行
我的编程:
#include <iostream>
using namespace std;
int a[100];
int sum_2 = 0,sum_5 = 0;
int main()
{
_for(i,0,100) RI(a[i]);
_for(i,0,100)
{
int tmp = a[i];
while(tmp%2==0)
{
tmp/=2;
sum_2++;
}
while(tmp%5==0)
{
tmp/=5;
sum_5++;
}
}
if(sum_2<sum_5) cout<<sum_2;
else cout<<sum_5;
return 0;
}
别人的编程:
#include <iostream>
#include<cstdio>
using namespace std;
struct node
{
int a2 , a5; //用来储存每个数质因子中 2 和 5 的个数;
};
struct node count(int num); //计算num 质因子中 2 和 5 的数量,并存在结构体中
int main()
{
int data[100];
for(int i = 0;i<100;i++)
{
cin>>data[i];
}
int len = sizeof(data) / sizeof(int);
int a5 = 0,a2 = 0;
for(int i = 0;i<len;i++)
{
a2 += count(data[i]).a2;
a5 += count(data[i]).a5;
}
printf("%d\n",a2 < a5 ? a2 : a5);
return 0;
}
struct node count(int num)
{
node temp;
for(int i = 2; i * i < num; i++)
{
int result = 0;
while(num % i == 0)
{
result++;
num /= i;
}
if(i == 2)
temp.a2=result;
else if(i == 5)
temp.a5=result;
}
if(num!=1)
{
if(num == 2)
temp.a2 = 1;
else if(num == 5)
temp.a5 = 1;
}
return temp;
}
别人的思路:
所有的 0 都一定是 2 * 5 产生的,所以将每个数拆成一堆 2 乘上一堆 5 再乘上一个数,之后统计下有多少个 2 和多少个 5 取少的那个就是答案
提问: 为啥所有的 10 都是 2 * 5 产生的呀?4 * 5,6 * 5 不是也可以吗?
回答: 可以是可以,但是本质上都是 2 * 5 得出的,你看 4 * 5,6 * 5不也是2 * 2 * 5,2 * 3 * 5 么,最后也都是一个 0,所以是一样的
我学到的:
所有的 0 都一定是 2 * 5 产生的,所以将每个数拆成一堆 2 乘上一堆 5 再乘上一个数,之后统计下有多少个 2 和多少个 5 取少的那个就是答案(这种思路要记住)
D-题目描述:测试次数(未)
x星球的居民脾气不太好,但好在他们生气的时候唯一的异常举动是:摔手机。
各大厂商也就纷纷推出各种耐摔型手机。x星球的质监局规定了手机必须经过耐摔测试,并且评定出一个耐摔指数来,之后才允许上市流通。
x星球有很多高耸入云的高塔,刚好可以用来做耐摔测试。塔的每一层高度都是一样的,与地球上稍有不同的是,他们的第一层不是地面,而是相当于我们的2楼。
如果手机从第7层扔下去没摔坏,但第8层摔坏了,则手机耐摔指数=7。
特别地,如果手机从第1层扔下去就坏了,则耐摔指数=0。
如果到了塔的最高层第n层扔没摔坏,则耐摔指数=n
为了减少测试次数,从每个厂家抽样3部手机参加测试。
某次测试的塔高为1000层,如果我们总是采用最佳策略,在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢?
请填写这个最多测试次数。
注意:需要填写的是一个整数,不要填写任何多余内容
答案:
19
我的思路:
无
别人编程:
#include<stdio.h>
#define Max(a,b) (a>b?a:b)
#define Min(a,b) (a<b?a:b)
int dp[1005][50];
int main(int argc, char* argv[])
{
int n,m;
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++)
{
dp[i][1]=i;
}
for (int cnt=2;cnt<=m;cnt++)
{
for (int ind=1;ind<=n;ind++)
{
dp[ind][cnt]=1+dp[ind-1][cnt];
for (int k=2;k<=ind;k++)
dp[ind][cnt]=Min(dp[ind][cnt],1+Max(dp[k-1][cnt-1],dp[ind-k][cnt]));
}
}
printf("%d\n",dp[n][m]);
return 0;
}
别人的思路:
我本来还想直接用二分法先交个答案算了,二分法求出的答案是log2(1000)=10,显然是错误的,因为二分法的话直接取中间的数,最坏的情况下你摔3次,3个手机就都爆了,你还怎么测,看到这么多分,还是得认真入坑
这道题其实是需要用动态规划或者记忆化搜索去解的,dp[x][y]表示当前还剩x楼不确定,还有y部手机没爆
我学到的:
这是编程方法的博客
其实还有另一种解决办法:
这是数学思维的博客
两种都想搞懂但都看不懂(回头看
E-题目描述:快速排序
以下代码可以从数组a[ ]中找出第k小的元素。
它使用了类似快速排序中的分治算法,期望时间复杂度是O(N)的。
请仔细阅读分析源码,填写划线部分缺失的内容
#include <stdio.h>
int quick_select(int a[], int l, int r, int k)
{
int p = rand() % (r - l + 1) + l;
int x = a[p];
{int t = a[p]; a[p] = a[r]; a[r] = t;}
int i = l, j = r;
while(i < j)
{
while(i < j && a[i] < x) i++;
if(i < j)
{
a[j] = a[i];
j--;
}
while(i < j && a[j] > x) j--;
if(i < j)
{
a[i] = a[j];
i++;
}
}
a[i] = x;
p = i;
if(i - l + 1 == k) return a[i];
if(i - l + 1 < k) return quick_select( _____________________________ ); //填空
else return quick_select(a, l, i - 1, k);
}
int main()
{
int a[] = {1, 4, 2, 8, 5, 7, 23, 58, 16, 27, 55, 13, 26, 24, 12};
printf("%d\n", quick_select(a, 0, 14, 5));
return 0;
}
我的思路:
第二次看,一开始还是莽填,但仔细看了题目和代码后才明白该如何写,虽然做出来了,但要让我自己把代码写出来还是不可能的,因为对于快排中的边界-1和+1我始终没有搞懂,即使背下模板遇到类型的题还是很迷,希望下次再看可以亲手写出来吧
我的答案:
(a, i + 1, r, k - ( i - l + 1 ) )
别人的答案:
(a, i + 1, r, k - ( i - l + 1 ) )
别人的思路:
由于返回的是第k小的数字,由代码我们可以分析出来,如果 i - l + 1 == k ,说明已经满足左边区域最后一个数字是第k大小的数字,
如果 小于k的话,我们就要在右边的区域寻找第 k - ( i - l + 1 ) 的数字,所以答案应该是 (a, i + 1, r, k - ( i - l + 1 ) ) 比赛的时候做了一下循环查找第i小的数字,都是对的
我学到的:
我错在没有分析直接莽填
F-题目描述:递增三元组
给定三个整数数组
A = [A1, A2, … AN],
B = [B1, B2, … BN],
C = [C1, C2, … CN],
请你统计有多少个三元组(i, j, k) 满足:
1、 1 <= i, j, k <= N
2、 Ai < Bj < Ck
【输入格式】
第一行包含一个整数N。
第二行包含N个整数A1, A2, … AN。
第三行包含N个整数B1, B2, … BN。
第四行包含N个整数C1, C2, … CN。
对于30%的数据,1 <= N <= 100
对于60%的数据,1 <= N <= 1000
对于100%的数据,1 <= N <= 100000 0 <= Ai, Bi, Ci <= 100000
【输出格式】
一个整数表示答案
【样例输入】
3
1 1 1
2 2 2
3 3 3
【样例输出】
27
我的思路:
无
别人的编程:
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 100005;
int a[MAXN],b[MAXN],c[MAXN];
long long n,sum;
int main()
{
cin>>n;
for(int i=0;i<n;i++)scanf("%d",&a[i]);
for(int i=0;i<n;i++)scanf("%d",&b[i]);
for(int i=0;i<n;i++)scanf("%d",&c[i]);
sort(a,a+n);
sort(b,b+n);
sort(c,c+n);
long long sum = 0;
for(int i=0;i<n;i++){
long long x = (lower_bound(a,a+n,b[i]) - a);
long long y = (n - (upper_bound(c,c+n,b[i]) - c));
sum += x*y;
}
cout<<sum;
return 0;
}
别人的思路:
可以先对三个数组排序,然后遍历数组b,查找a数组中有多少个小于b[i]的,c数组中有多少个大于b[i]的
我学到的:
关于lower_bound( )和upper_bound( )都是利用二分查找的方法在一个排好序的数组中进行查找的
在从小到大的排序数组中:
lower_bound( begin,end,num):从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字,找到返回该数字的地址,不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标
upper_bound( begin,end,num):从数组的begin位置到end-1位置二分查找第一个大于num的数字,找到返回该数字的地址,不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标
int pos1 = lower_bound(num,num+6,7)-num; //返回数组中第一个大于或等于 7 的下标或 6(没找到)
int pos2 = upper_bound(num,num+6,7)-num; //返回数组中第一个大于 7 的下标或 6(没找到)
在从大到小的排序数组中,重载lower_bound()和upper_bound():
lower_bound( begin,end,num,greater< type >( ) ):从数组的begin位置到end-1位置二分查找第一个小于或等于num的数字,找到返回该数字的地址,不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标
upper_bound( begin,end,num,greater< type >( ) ):从数组的begin位置到end-1位置二分查找第一个小于num的数字,找到返回该数字的地址,不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标
int pos3 = lower_bound(num,num+6,7,greater<int>())-num; //返回数组中第一个小于或等于 7 的下标或 6(没找到)
int pos4 = upper_bound(num,num+6,7,greater<int>())-num; //返回数组中第一个小于 7 的下标或 6(没找到)
以 lower_bound(a,a+n,b[i]) - a 举例,若要历遍整个数组,则第二个参数减第一个参数等于 n,并且最后记得减 a
(n - (upper_bound(c,c+n,b[i]) - c))之所以用upper_bound是因为所求个数是包括大于等于的元素的
其实对于左闭右开(即begin位置到end-1位置)是因为 n 是包括0号元素的,所以会多一个元素出来,因此要 -1
G-题目描述:螺旋折线

如图所示的螺旋折线经过平面上所有整点恰好一次。
对于整点(X, Y),我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。
例如dis(0, 1)=3, dis(-2, -1)=9
给出整点坐标(X, Y),你能计算出dis(X, Y)吗?
【输入格式】
X和Y
对于40%的数据,-1000 <= X, Y <= 1000
对于70%的数据,-100000 <= X, Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000
【输出格式】
输出dis(X, Y)
【样例输入】
0 1
【样例输出】
3
我的思路:
看的出 dis 的长度是如此增加的:1、1、2、2、3、3、4、4、5、5…但不知道如何利用
别人的编程:
#include <bits/stdc++.h>
using namespace std;
typedef long int l;
int main()
{
l x,y,n,length,sum;
cin>>x;
cin>>y;
n = (labs(x)>labs(y))?labs(x):labs(y);
//计算前面几个正方形的长度
length = 4*(n-1)*n; //等差数列求和
//计算距离(-n,-n)的距离
if(y>x)
{
sum = (x+n) + (y+n);
}
else
{
sum = 8*n - ((x+n) + (y+n));
}
cout<< sum + length <<endl;
return 0;
}
别人的思路:
我的方法是去算正方形的长度,仔细观察这张图,我们只要把左下的一条边顺时针旋转90°,就能得到一个矩形

然后我们只要操作两个步骤:
1. 计算这个点之前的所有正方形
2. 计算这个点所在的几条边
设计步骤
我们举个例子,假设我们要计算point(-1, 2)这个点
第一个步骤相当简单,我们发现每个正方形都是一个等差数列
这个数列是8, 16, 24, 32....
所以我们拿前n项和公式来算就行,注意算这个点之前所在所有正方形的和
第二个步骤需要一些技巧,我们发现,我们将左下的边旋转之后,对应着的点是(-1, -1), (-2, -2), (-3, -3)....(-n, -n)
所以我们从这个点开始,计算这个点到point的边距离
最后我们加上两个步骤算出来的距离,就得到了答案
我学到的:
新颖的思维
等差、等比还是要背熟的
最后计算距离 (-n,-n) 的距离的时候是以 y = x 这条线分类讨论的,在的左上方即有 y > x ,那么实际距离可以直接想加(减减为加),同理在右下方可以用总长度减实际距离
H-题目描述:全球变暖
你有一张某海域NxN像素的照片,".“表示海洋、”#"表示陆地,如下所示:
.......
.##....
.##....
....##.
..####.
...###.
.......
其中"上下左右"四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有2座岛屿。
由于全球变暖导致了海面上升,科学家预测未来几十年,岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。
例如上图中的海域未来会变成如下样子:
.......
.......
.......
.......
....#..
.......
.......
请你计算:依照科学家的预测,照片中有多少岛屿会被完全淹没。
【输入格式】
第一行包含一个整数N。 (1 <= N <= 1000)
以下N行N列代表一张海域照片。
照片保证第1行、第1列、第N行、第N列的像素都是海洋。
【输出格式】
一个整数表示答案
【输入样例】
7
.......
.##....
.##....
....##.
..####.
...###.
.......
【输出样例】
1
别人的思路:
很多人包括我起初都误求为剩下的岛屿。先求原来有多少岛屿,然后再将沿海的岛屿淹没,最后求剩下的岛屿。淹没的岛屿数 = 原来的 - 剩下的(注意:可能为出现负数)
深搜岛屿然后处理淹没范围最后判断,有一点值得注意的是有可能海水侵蚀完后可能岛屿更多了,就是类似于这样的样例容易出错
别人的编程:
#include <iostream>
#include <cstring>
using namespace std;
int n;
char map[2][1005][1005];
bool vis[1005][1005];
void dfs(int d, int x, int y) {
if (x<0 || x>=n || y<0 || y>=n || vis[x][y] || map[d][x][y]!='#')
return;
vis[x][y] = true;
map[d][x][y] = '.';
dfs(d, x+1, y);
dfs(d, x-1, y);
dfs(d, x, y+1);
dfs(d, x, y-1);
return;
}
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> map[0][i][j];
map[1][i][j] = map[0][i][j];
}
}
//判断原来多少个岛屿
int cnt1 = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (!vis[i][j] && map[0][i][j]=='#') {
cnt1++;
dfs(0, i, j);
}
}
}
memset(vis, false, sizeof(vis)); // 及时清空
//如果一块陆地周围是海,则变成海
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (map[1][i][j]=='#') {
if (i!=0 && j!=0) {
if (map[1][i+1][j]=='.' || map[1][i-1][j]=='.' || map[1][i][j+1]=='.' || map[1][i][j-1]=='.')
map[1][i][j] = '*'; // *表示下沉的陆地
} else if (i == 0) {
if (map[1][i+1][j]=='.' || map[1][i][j+1]=='.' || map[1][i][j-1]=='.')
map[1][i][j] = '*'; // *表示下沉的陆地
} else if (j == 0) {
if (map[1][i+1][j]=='.' || map[1][i-1][j]=='.' || map[1][i][j+1]=='.')
map[1][i][j] = '*'; // *表示下沉的陆地
}
}
}
}
//求剩下的岛屿
int cnt2 = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (!vis[i][j] && map[1][i][j]=='#') {
cnt2++;
dfs(1, i, j);
}
}
}
int ans = cnt1 - cnt2; // 淹没的岛屿数 = 原来的 - 剩下的
if (ans <= 0) cout << 0 << endl;
else cout << ans << endl;
return 0;
}
/*
题目求的是淹没了多少岛屿,而不是剩下多少
7
.......
.##....
.##....
....##.
..####.
...###.
.......
1
7
.......
.##....
.##....
....##.
..####.
#..###.
##.....
1
7
..#....
.###...
.##....
....##.
..####.
#..###.
##.....
0
7
.......
.......
.......
##..###
#######
##..###
.......
0
7
#######
#######
#######
#######
#######
#######
#######
0
7
.......
.......
.......
.......
.......
.......
.......
0
*/
我的思路:
我对他的代码进行了改进,首先删除了标记数组(因为根本用不到),然后在中间删除 '#' 的处增加了i==0&&j==0,虽然他的没有这个条件也通过了测试,但是加上会使代码更具完整性,一眼就知道所有讨论的情况
我的编程:
#include <sstream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <iostream>
#include <vector>
#include <algorithm>
#include <iterator>
#include <string>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define _for(i,a,b) for(int i=a;i<b;i++)
#define _unfor(i,a,b) for(int i=a;i>=b;i--)
#define RI(a) scanf("%d",&a)
#define mset(a,val,n) for(int i=0;i<n;i++)a[i]=val;
#define mset2(a,val,n,m) for(int i=0;i<n;i++)for(int j=0;j<m;j++)a[i][j]=val;
#define FI freopen("D:\\in.txt","r",stdin)
#define FO freopen("D:\\out.txt","w",stdout)
using namespace std;
typedef long long LL;
/*-------下面为主要代码-------*/
int cnt,ans,result,n;
char mp[2][1001][1001];
int vir[1001][1001];
void dfs(int i,int j,int z)
{
if(mp[z][i][j]!='#'||i<0||i>n-1||j<0||j>n-1) return;//标记、越界
mp[z][i][j]='.';
dfs(i+1,j,z);
dfs(i-1,j,z);
dfs(i,j+1,z);
dfs(i,j-1,z);
}
int main()
{
cin>>n;
_for(i,0,n) _for(j,0,n)
{
cin>>mp[0][i][j];
mp[1][i][j]=mp[0][i][j];
}
//
_for(i,0,n) _for(j,0,n)
{
if(mp[0][i][j]=='#')
{
cnt++;
dfs(i,j,0);
}
}
//
_for(i,0,n) _for(j,0,n) if(mp[1][i][j]=='#')
{
if(i!=0&&j!=0) if(mp[1][i+1][j]=='.'||mp[1][i-1][j]=='.'||mp[1][i][j+1]=='.'||mp[1][i][j-1]=='.') mp[1][i][j]='*';
else if(i==0&&j==0) if(mp[1][i+1][j]=='.'||mp[1][i][j+1]=='.') mp[1][i][j]='*';
else if(i==0&&j!=0) if(mp[1][i+1][j]=='.'||mp[1][i][j+1]=='.'||mp[1][i][j-1]=='.') mp[1][i][j]='*';
else if(mp[1][i+1][j]=='.'||mp[1][i-1][j]=='.'||mp[1][i][j+1]=='.') mp[1][i][j]='*';
}
//
_for(i,0,n) _for(j,0,n)
{
if(mp[1][i][j]=='#')
{
ans++;
dfs(i,j,1);
}
}
result = cnt-ans;
cout<<result;
return 0;
}
需要注意的:
1、设置用来记录地图的数组要用 char 型
2、注意在删除 '#' 时,要改为 '*' 而不是 '.' ,不然接下来的循环会把 '.' 当成原来的 '.'
3、之所以可以在删除 '#' 时忽略右边与下边的越界问题,是因为最初设置数组时 mp 数组的第一维数组(代表下边)和第二维数组(代表右边)多了一个元素,故不会越界
I-题目描述:乘积最大
给定N个整数A1, A2, … AN。请你从中选出K个数,使其乘积最大。
请你求出最大的乘积,由于乘积可能超出整型范围,你只需输出乘积除以1000000009的余数。
注意,如果X<0, 我们定义X除以1000000009的余数是负(-X)除以1000000009的余数。
即:0-((0-x) % 1000000009)
【输入格式】
第一行包含两个整数N和K。
以下N行每行一个整数Ai。
对于40%的数据,1 <= K <= N <= 100
对于60%的数据,1 <= K <= 1000
对于100%的数据,1 <= K <= N <= 100000
-100000 <= Ai <= 100000
【输出格式】
一个整数,表示答案。
【输入样例】
5 3
-100000
-10000
2
100000
10000
【输出样例】
999100009
再例如:
【输入样例】
5 3
-100000
-100000
-2
-100000
-100000
【输出样例】
-999999829
别人的思路:
这题我觉得贪心分情况即可:先按照绝对值从大到小排序
①假如选的k个数中必定有0,则结果为0
②假如都是负数,此时若k为偶数,则选前k个数即可,若k为奇数,则只能从小的开始选k个数
③假如都为正数,选前k个数即可
④假如正负都有,此时,若前k个数有偶数个负数,则选前k个数即可
若前k个数有奇数个负数,则我们看看能不能从后面选一个大正数跟前面的小负数做交换,或者从后面选一个大负数跟前面的小正数做交换,二者取结果大的
此时分完所有情况若结果还为负数,我们看看输入是否有0,有零结果即为0,否则就只能输出这个负数了
别人的编程:
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
#define mod 1000000009
using namespace std;
typedef long long ll;
const int maxn = 1e6+5;
const double esp = 1e-7;
const int ff = 0x3f3f3f3f;
map<int,int>::iterator it;
struct node
{
ll x;
int f;
}a[maxn];
int n,k;
bool cmp(node x,node y)
{
return x.x> y.x;
}
ll solve(int o)
{
ll ans = 1;
int cnt = 0;
if(o == 0)//从前往后乘
{
for(int i = 1;i<= k;i++)
{
ans = (ans*a[i].x)%mod;
if(a[i].f == 1)
cnt++;
}
}
else//从后往前乘
{
for(int i = n;i> n-k;i--)
{
ans = (ans*a[i].x)%mod;
if(a[i].f == 1)
cnt++;
}
}
if(cnt&1)
return ans*(-1);
return ans;
}
int main()
{
cin>>n>>k;
int flag = 0;
int cnt = 0;
for(int i = 1;i<= n;i++)
{
scanf("%lld",&a[i].x);
if(a[i].x< 0)
{
a[i].f = 1;
a[i].x = -a[i].x;
cnt++;
}
else if(a[i].x> 0)
a[i].f = 0;
else
{
i--;n--;//我们不记录0,0只做迫不得已的选择
flag = 1;
}
}
sort(a+1,a+n+1,cmp);
ll ans = 0;
if(n< k)//如果必须选0
ans = 0;
else if(cnt == n)//如果都为负数
{
if(k&1)
ans = solve(1);
else
ans = solve(0);
}
else if(cnt == 0)//如果都为正数
ans = solve(0);
else
{
int tmp = 0;
for(int i = 1;i<= k;i++)
if(a[i].f == 1)
tmp++;
if(tmp%2 == 0)//如果前k大的数有偶数个负数
ans = solve(0);
else
{
ans = -1;//将其设置为负数
//尝试将前k个里面一个绝对值最小负数和后面最大正数交换
int p = -1,q = -1;
for(int i = k+1;i<= n;i++)
if(a[i].f == 0)
{
q = i;
break;
}
for(int i = k;i>= 1;i--)
if(a[i].f == 1)
{
p = i;
break;
}
if(p!= -1&&q!= -1)
{
swap(a[p],a[q]);
ans = solve(0);
swap(a[p],a[q]);
}
//尝试将前k个里面一个最小正数和后面绝对值最大正数交换
p = -1,q = -1;
for(int i = k+1;i<= n;i++)
if(a[i].f == 1)
{
q = i;
break;
}
for(int i = k;i>= 1;i--)
if(a[i].f == 0)
{
p = i;
break;
}
if(p!= -1&&q!= -1)
{
swap(a[p],a[q]);
ans = max(ans,solve(0));
swap(a[p],a[q]);
}
//假如结果仍然小于0,我们只能尝试从最后往前乘了
if(ans< 0)
ans = solve(1);
}
}
if(ans< 0)
if(flag)//这时候0派上用场了
{
cout<<0<<endl;
return 0;
}
cout<<ans<<endl;
return 0;
}
我的思路
我按照他的思路又写了一遍,但过不了第一组样例,日后再重新看一遍吧
我的编程:
#include <sstream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <iostream>
#include <vector>
#include <algorithm>
#include <iterator>
#include <string>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define _for(i,a,b) for(int i=a;i<b;i++)
#define _unfor(i,a,b) for(int i=a;i>=b;i--)
#define RI(a) scanf("%d",&a)
#define mset(a,val,n) for(int i=0;i<n;i++)a[i]=val;
#define mset2(a,val,n,m) for(int i=0;i<n;i++)for(int j=0;j<m;j++)a[i][j]=val;
#define FI freopen("D:\\in.txt","r",stdin)
#define FO freopen("D:\\out.txt","w",stdout)
using namespace std;
typedef long long LL;
/*-------下面为主要代码-------*/
#define mod 1000000009
struct Step
{
LL x;
int f;
}a[100001];
bool cmp(Step x,Step y) //用于在sort函数中比较结构体成员大小
{
return x.x>y.x;
}
LL n,k; //之所以n、k写在这里是因为下面这个函数要用到
LL solve(int t) //作用是返回前 k个(或后 k个)数相乘的结果,注意有返回值,且为 LL
{
LL ans=1; //记录最终结果
int tmp=0; //统计负数数目
if(t==1) //从前往后乘
{
_for(i,1,k+1)
{
if(a[i].f==1) tmp++;
ans = (ans*a[i].x)%mod; //记得取模
}
}
else //从后往前乘
{
_unfor(i,n,n-k+1) //这里实际上相当于 for(int i = n;i> n-k;i--)
{
if(a[i].f==1) tmp++;
ans = (ans*a[i].x)%mod;
}
}
if(tmp&1==1)
{
return ans*(-1); //若有奇数个负数,则输出负数
}
else return ans;
}
int main()
{
LL ans; //ans是最后的结果
int cnt=0,flag=0; //cnt记录有多少正数,flag记录是否存在 0
cin>>n>>k;
_for(i,1,n+1) //从 1开始记数
{
scanf("%lld",&a[i].x);
if(a[i].x<0) {a[i].f=1;a[i].x=(-1)*a[i].x;cnt++;} //小于 0,记得要记录绝对值
else if(a[i].x>0) a[i].f=0; //大于 0
else //等于 0
{
flag=1; //只记录,不接收
n--;i--; //这为后面四个判断做了很大贡献
}
}
sort(a+1,a+n+1,cmp); //只用排序非 0的数,加了cmp代表是结构体成员比较
if(n<k) ans = 0; //若必须选 0,
else if(cnt==n) //若全负
{
if(k&1) //数目为奇数
ans = solve(0);
else //数目为偶数
ans = solve(1);
}
else if(cnt==0) ans = solve(1); //若全正
else //若有正数也有负数
{
cnt=0; //重新赋值cnt,现在它统计前 k个数的负数数目
_for(i,1,k+1) if(a[i].f==1) cnt++;
if(cnt&1==0) ans = solve(1); //若cnt是偶数
else //若cnt是奇数
{
ans = -1; //将 ans先设置为-1,因为在这里ans无论如何都不可能为负数的(除了一种情况)
//第一种方法:将前 k个最小的正数 与 后面绝对值最大的负数交换
int p=-1,q=-1; //记录前面最小的正数的下标 ,后面绝对值最大的负数的下标
_unfor(i,k,1) //找最小的正数的下标
{
if(a[i].f==0) p=i;
}
_for(i,k+1,n) //找后面绝对值最大的负数的下标
{
if(a[i].f==1) q=i;
}
if(p!=-1&&q!=-1) //p、q都存在时
{
swap(a[q],a[p]);
ans = solve(1);
swap(a[q],a[p]);
}
//第二种到底:将前 k个绝对值最小的负数 与后面最大的正数交换
p=-1;q=-1; //记录前面最小的正数的下标 ,后面绝对值最大的负数的下标
_unfor(i,k,1) //找绝对值最小的负数的下标
{
if(a[i].f==1) p=i;
}
_for(i,k+1,n) //找后面最大的正数的下标
{
if(a[i].f==0) q=i;
}
if(p!=-1&&q!=-1)
{
swap(a[q],a[p]);
ans = max(solve(1),ans);
swap(a[q],a[p]);
}
if(ans<0) ans=solve(0); //这种情况就是:只有两个数字,且一个是正数一个是负数,目标求两者相乘
}
}
if(ans<0) if(flag==1) ans = 0; //若最后结果依然为负数但存在 0,结果则 ans为 0
cout<<ans;
return 0;
}
注意事项
虽然思路是本题的核心,但是写代码时也有许多要注意的,比如
1、sort()中的 cmp是用来比较结构体成员的
2、还有很重要的:变量,全局变量、局部变量的相互使用会导致很多bug,我样例不过的原因就是使用不当,至今未找出bug
3、LL 和 int 的使用也要谨慎
4、tmp&1 代表是判断 tmp 奇偶性的,结果为 1 即奇数,结果为 0 即偶数





















 1804
1804

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








