数据结构-图的遍历和应用(DAG、AOV、AOE网)

本文链接：https://blog.csdn.net/CyAurora/article/details/130566185

本文介绍了图的两种主要遍历方法——广度优先遍历(BFS)和深度优先遍历(DFS)，以及它们在生成树和生成森林中的应用。同时，讨论了寻找最小生成树的Prim和Kruskal算法，解决最短路径问题的BFS、Dijkstra和Floyd算法。此外，还涵盖了有向无环图(DAG)、拓扑排序及其逆过程，以及关键路径分析在AOE网中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

*一、广度优先遍历(BFS)

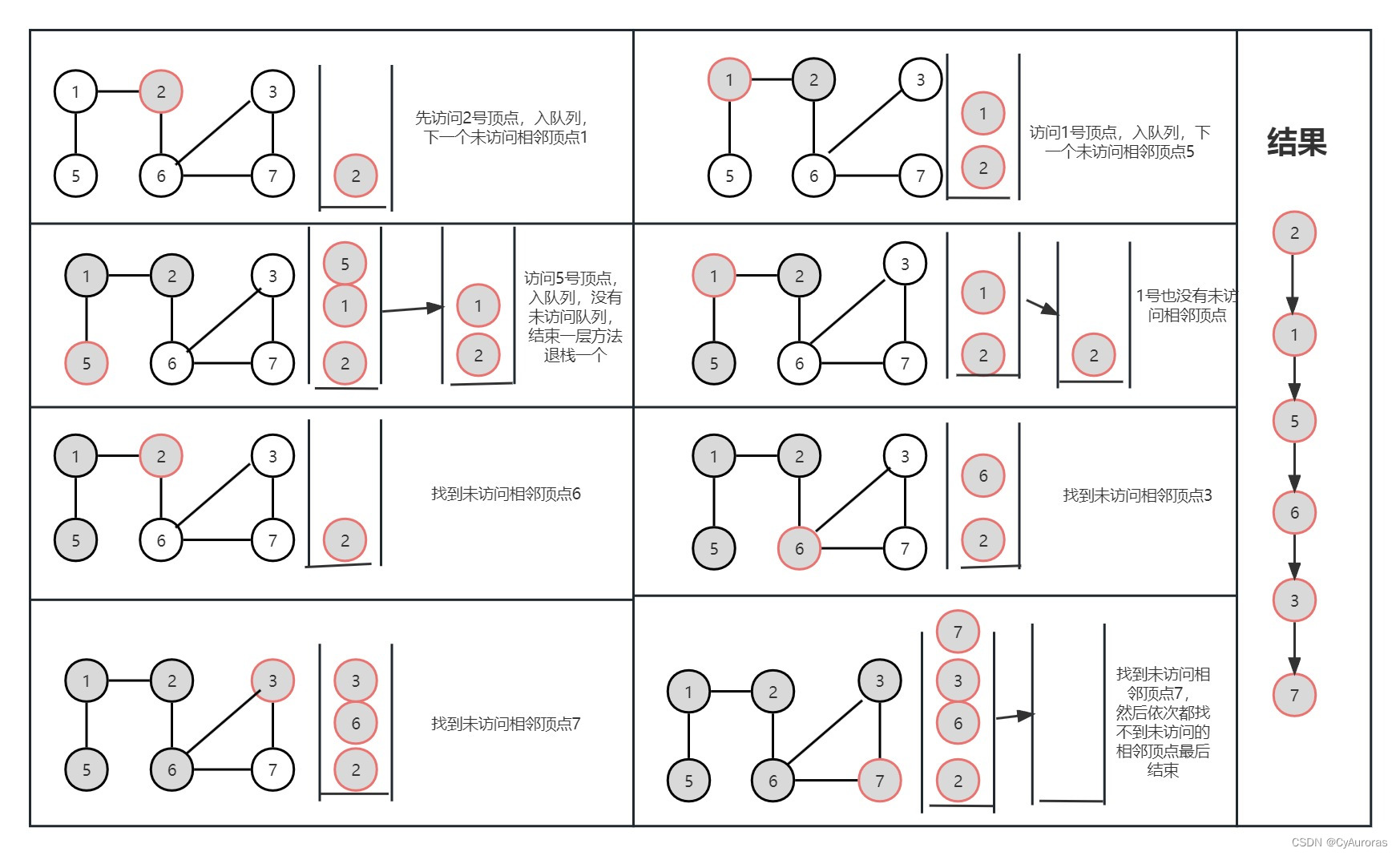
类似树的广度遍历

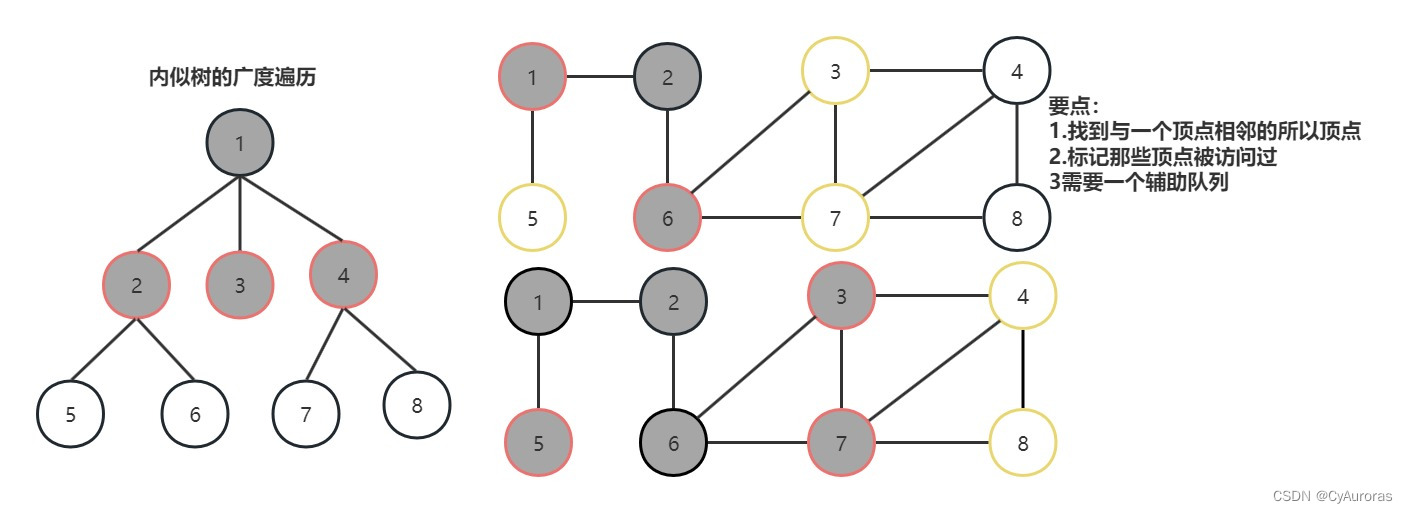
FirstNeighbor(G,x)：求图G中顶点x的第一个邻接点，若有则返回顶点号，没有返回-1

NextNrighbor(G,x,y)：假设图G中顶点y是顶点x的邻接点，返回除y之外顶点x的下一个邻接点的顶点号，若y就是最后一个返回-1

bool visited[MAX_VERTEX_NUM];        //访问标记数组
void BFS(Graph G,int v){
    visit(v);                        //访问初始顶点v
    visited[v]=TRUE;                 //对v做已访问标记
    Enqueue(Q,v);                    //入队列
    while(!isEmpty(Q)){              
        Dequeue(Q,v);                //顶点v出队
        for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w)){ //检测v所以邻接点
            if(!visited[w]){
                visit(w);            //访问顶点w
                visited[w]=TRUE;     //对w做已访问标记
                Enqueue(Q,w);        //入队列
            }
        }
    }
}

void BFSraverse(Graph G){
    for(i=0;i<G.vexnum;++i)
        visired[i]=FASLE;        //初始化标记数组
    InitQueue(Q);                //初始化辅助队列
    for(i=0;i<G.vexnum;++i)
        if(!visited[i])          //对每个连通分量调用一次BFS
            BFS(G,i);
}

空间复杂度：最坏。辅助队列O(V)

邻接矩阵时间复杂度： $\tiny O(V^2)$

邻接表时间复杂度： $\tiny O(V+E)$

广度优先生成树

邻接表生成不唯一，具体看数据先后顺序

广度优先生成森林

一个连通分量一个树，多个(非连通图)就是森林

*二、深度优先遍历

类似树的先序遍历

bool visited[MAX_VERTEX_NUM];      //访问标记数组
void DFS(Graph G,int v){
    visit(v);                      //访问v
    visited[v]=TRUE;               //标记已访问
    for(w=FirstNeighbor(G,V);w>=0;w=NextNeighor(G,v,w))    //邻接顶点
        if(!visited[w]){
            DFS(G,w);   
        }

}

void DFSraverse(Graph G){
    for(v=0;v<G.vwxnum;++v)
        visited[v]=FALSE;
    for(v=0;v<G.vexnum;++v)
        if(!visited[v])
            DFS(G,v);
}

空间复杂度：最后O(1) ,最坏情况:O(V)

邻接矩阵时间复杂度： $\tiny O(V^2)$

邻接表时间复杂度： $\tiny O(V+E)$

邻接表存储顺序性不一致，遍历序列不一样

深度优先生成树

邻接表生成不唯一，具体看数据先后顺序

深度优先生成森林

一个连通分量一个树，多个(非连通图)就是森林

二、应用

2.1最小生成树

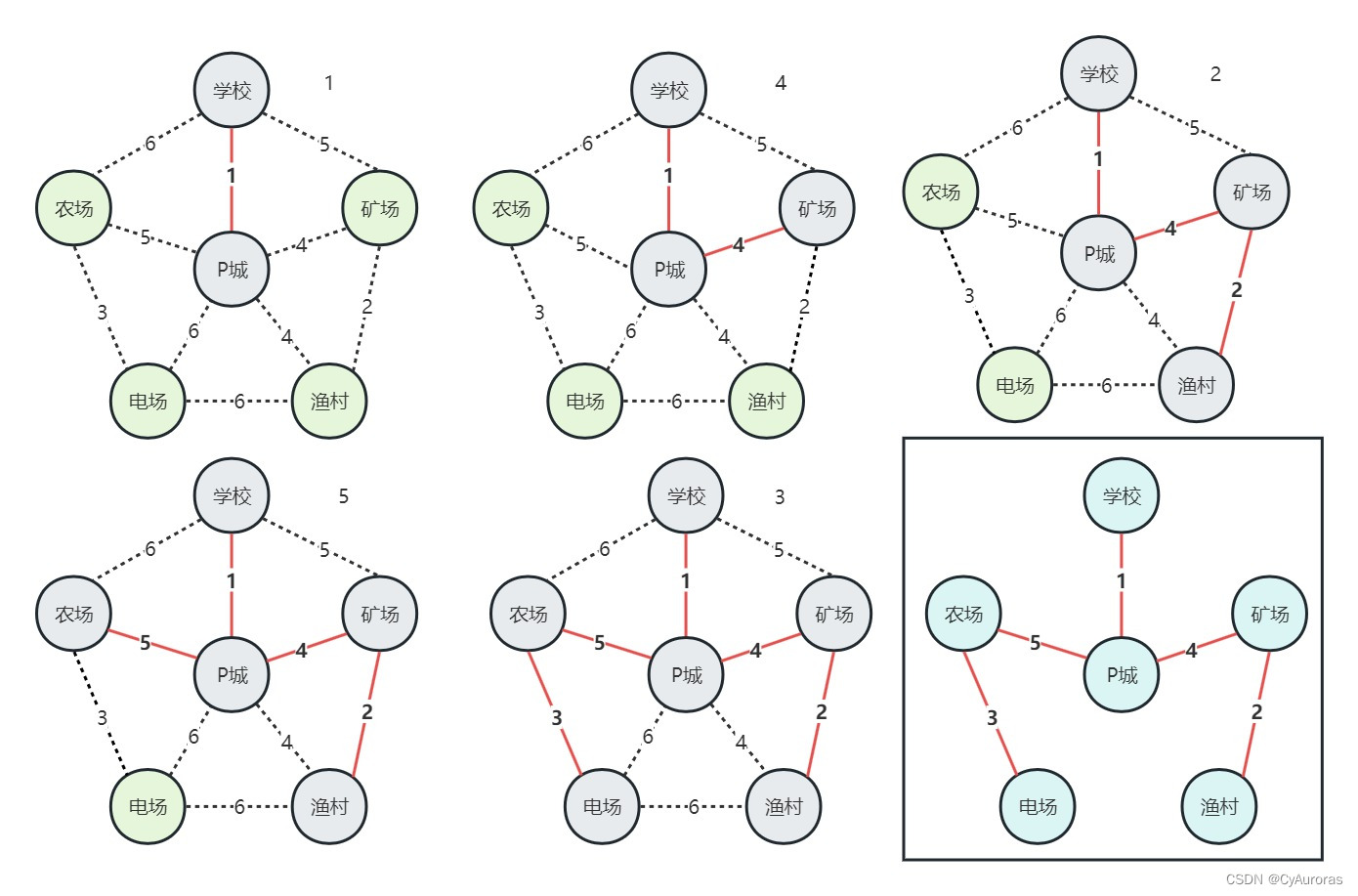
*Prim算法

从某一个顶点开始构建生成树；每一次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止

时间复杂度： $\tiny O(V^2)$ 适用于边稠密图

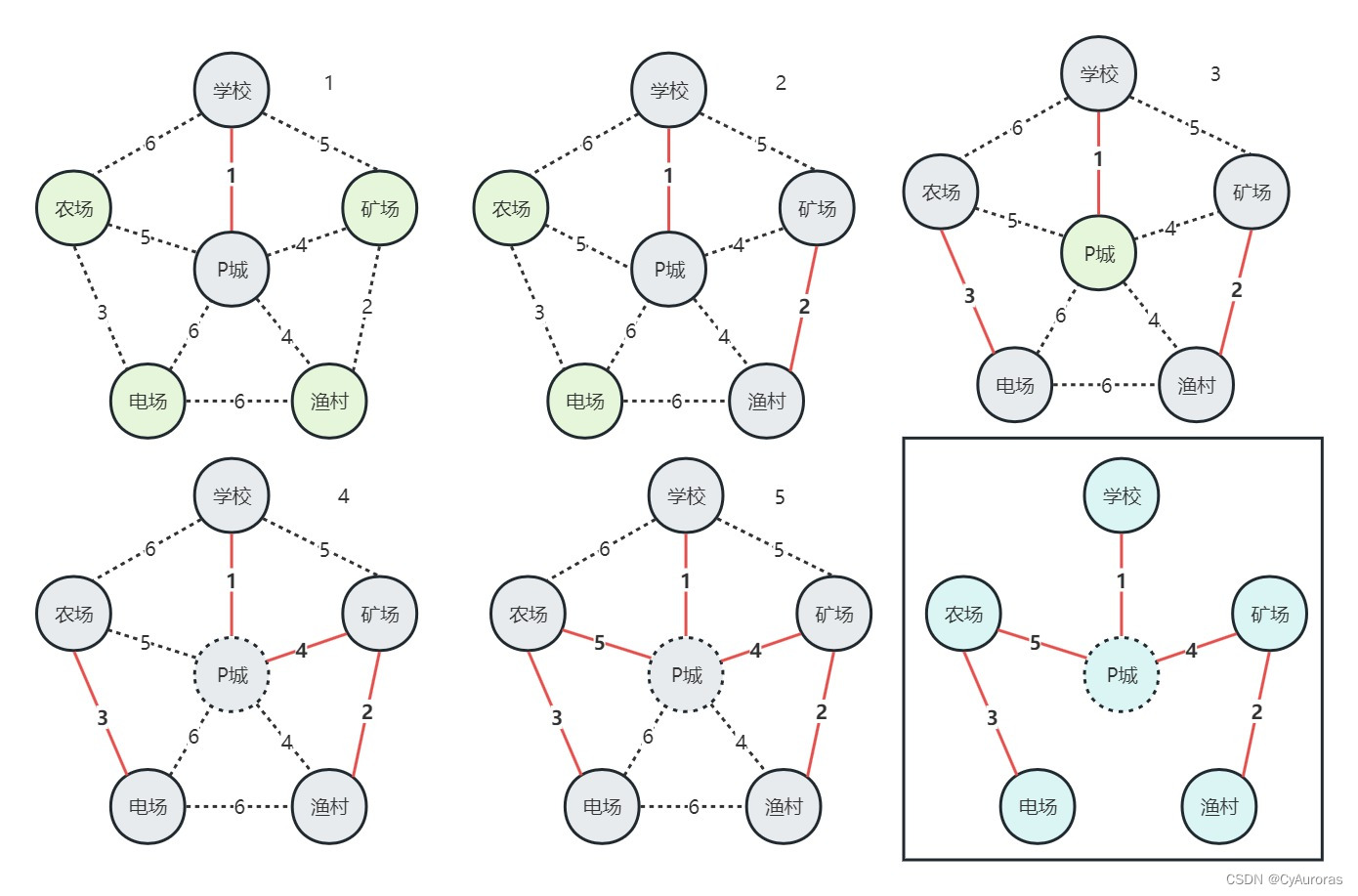
*Kruskal算法

每次选择一条权值最小边，使这条边两头连通(已经连通不用)，直到所有结点连通

时间复杂度： $\tiny O(elog_2e)$ 适合用于边稀疏图

2.2最短路径

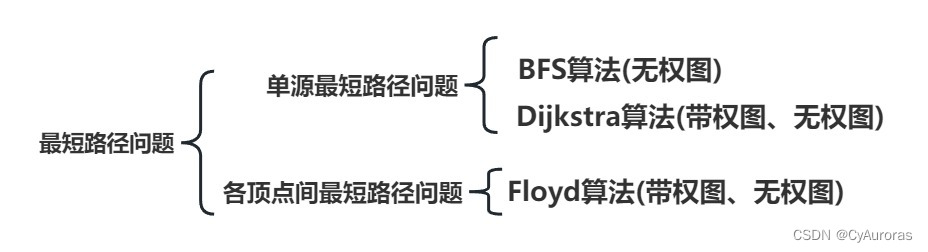
*BFS算法

*Dijkstra算法

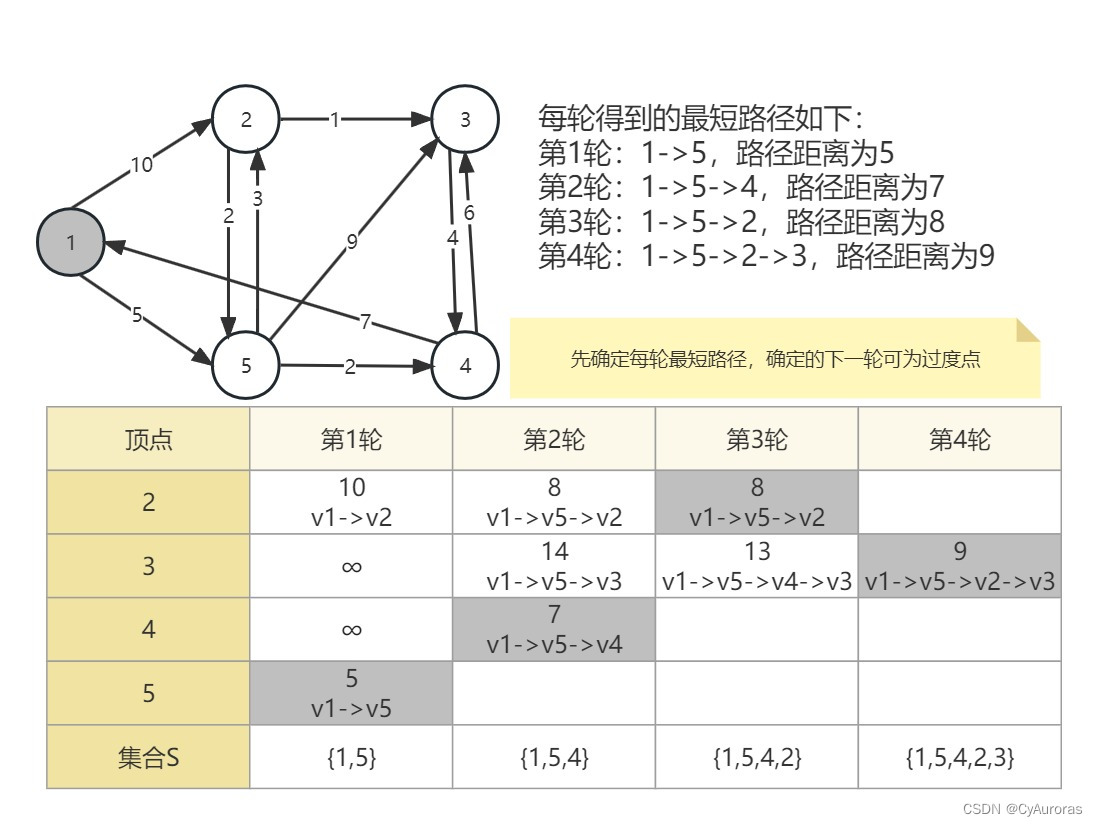
*Floyd算法

动态规划思想

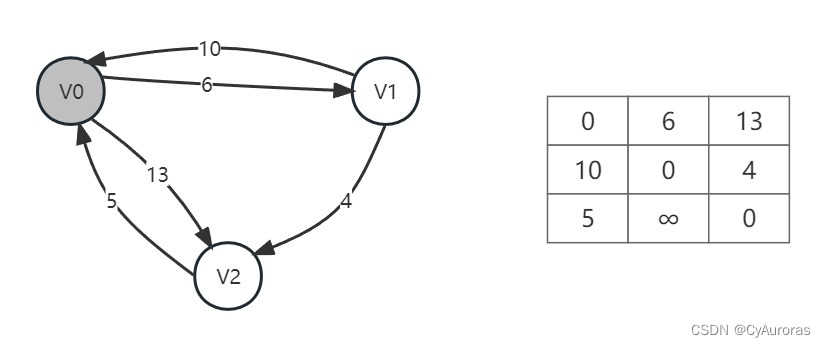
每轮看 $\tiny A^{-1}[i][j]>A^{-1}[i][n]+A^{-1}[n][j]$ ,n为第几轮，n也就是几个顶点为中转点

$\tiny A^{(2)}$ =	A	$\tiny A^{(-1)}$			$\tiny A^{(0)}$			$\tiny A^{(1)}$			$\tiny A^{(2)}$
		$\tiny V_0$	$\tiny V_1$	$\tiny V_2$	$\tiny V_0$	$\tiny V_1$	$\tiny V_2$	$\tiny V_0$	$\tiny V_1$	$\tiny V_2$	$\tiny V_0$	$\tiny V_1$	$\tiny V_2$
	$\tiny V_0$	0	6	13	0	6	13	0	6	10	0	6	10
	$\tiny V_1$	10	0	4	10	0	4	10	0	4	9	0	4
	$\tiny V_2$	5	∞	0	5	11	5	5	11	0	5	11	0

中转点为第几轮换的就是几

$\tiny path^{(2)}$ =		$\tiny V_0$	$\tiny V_1$	$\tiny V_2$
	$\tiny V_0$	-1	-1	1
	$\tiny V_1$	2	-1	-1
	$\tiny V_2$	-1	0	-1

第一轮( $\tiny A^{(0)}$ )： $\tiny A^{-1}[i][j]>A^{-1}[i][0]+A^{-1}[0][j]$ ，更新值

第二轮( $\tiny A^{(1)}$ )： $\tiny A^{-1}[i][j]>A^{-1}[i][1]+A^{-1}[1][j]$

第三轮( $\tiny A^{(2)}$ )： $\tiny A^{-1}[i][j]>A^{-1}[i][2]+A^{-1}[2][j]$

几个顶点几轮

根据上面 $\tiny A^{(2)}$ 可知 $\tiny V_1$ 到 $\tiny V_2$ 最短路径为4，根据 $\tiny path^{(2)}$ 为-1没有中转，路径为 $\tiny V_1->V_2$

根据上面 $\tiny A^{(2)}$ 可知 $\tiny V_0$ 到 $\tiny V_2$ 最短路径为10, 根据 $\tiny path^{(2)}$ 为1,经过 $\tiny V_1$ 顶点中转，路径为 $\tiny V_0->V_1->V_2$

for(int k=0;k<n;lk++){                       //考虑vk为中转点
    for(int i=0;i<n;i++){                    //遍历矩阵，i行，j列
        for(int j=0;j<n;j++){
            if(A[i][j]>A[i][k]+A[k][j]){     //以vk为中转点的路径更短
                A[i][j]=A[i][k]+A[k][j];     //最短路径
                path[i][j]=k;                //中转点
            }
        }
    }
}

时间复杂度： $\tiny O(V^3)$

空间复杂度： $\tiny O(V^2)$

*2.3有向无环图(DAG网)

若一个有向图中不存在环，则称为有向无环图，简称DAG图

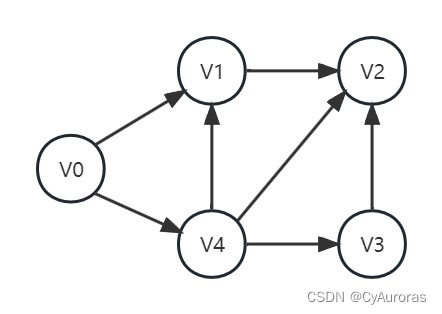
有向无环图是描述含有公共子式的表达式的有效工具，列如表达式 $\tiny ((a+b)*(b*(c+d))+(c+d)*e)*((c+d)*e)$

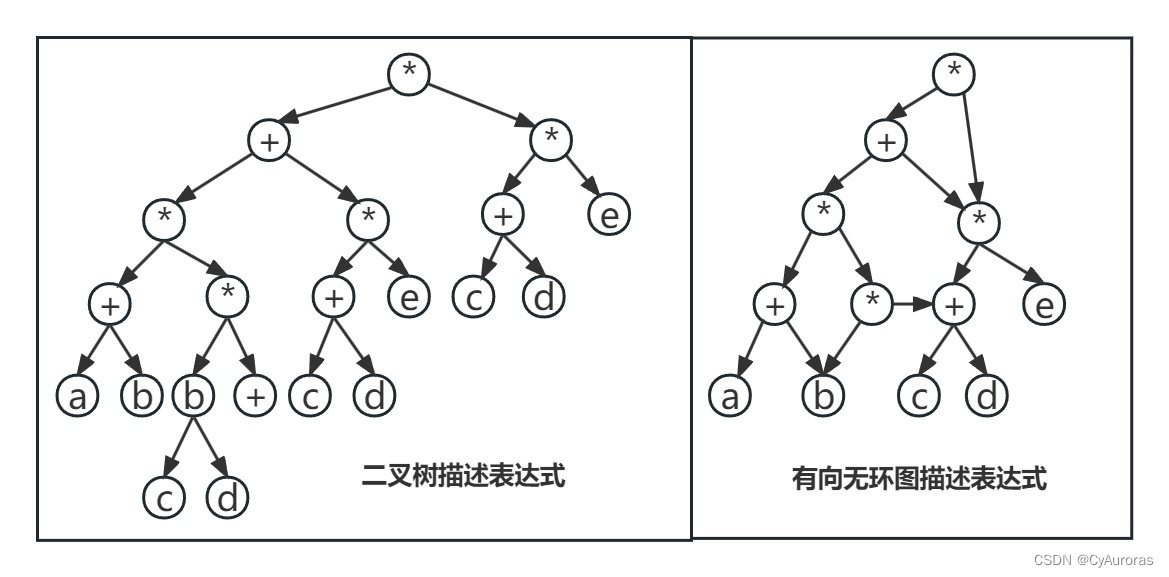
DAG不可能出现重复操作数

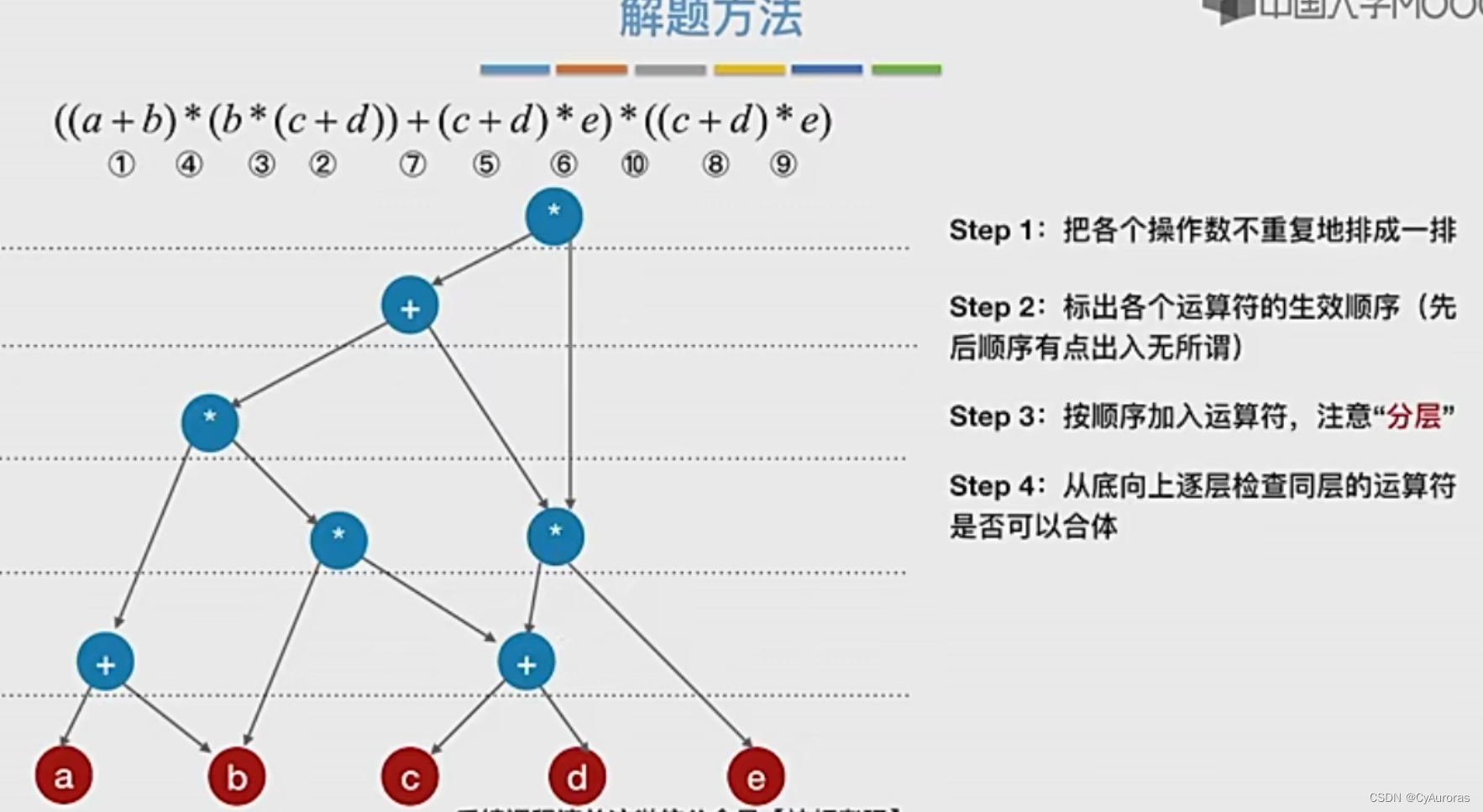
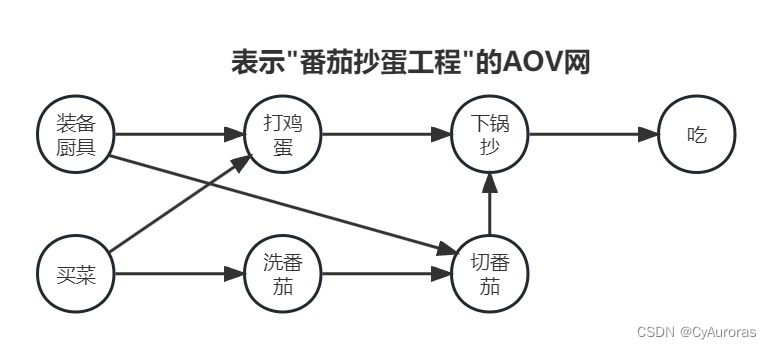
*2.4拓扑排序(AOV网)

AOV网：若用DAG图表示一个工程图，其顶点表示活动，用边表示活动 $\tiny V_i$ 必选先于活动 $\tiny V_j$ 进行的这样一种关系，则这种有向图称顶点表示活动的网络，记为AOV网。 $\tiny V_i$ 是 $\tiny V_j$ 的直接前驱， $\tiny V_j$ 是 $\tiny V_i$ 直接后继，不能自己做自己的前驱和后继。每个工程只出现一次

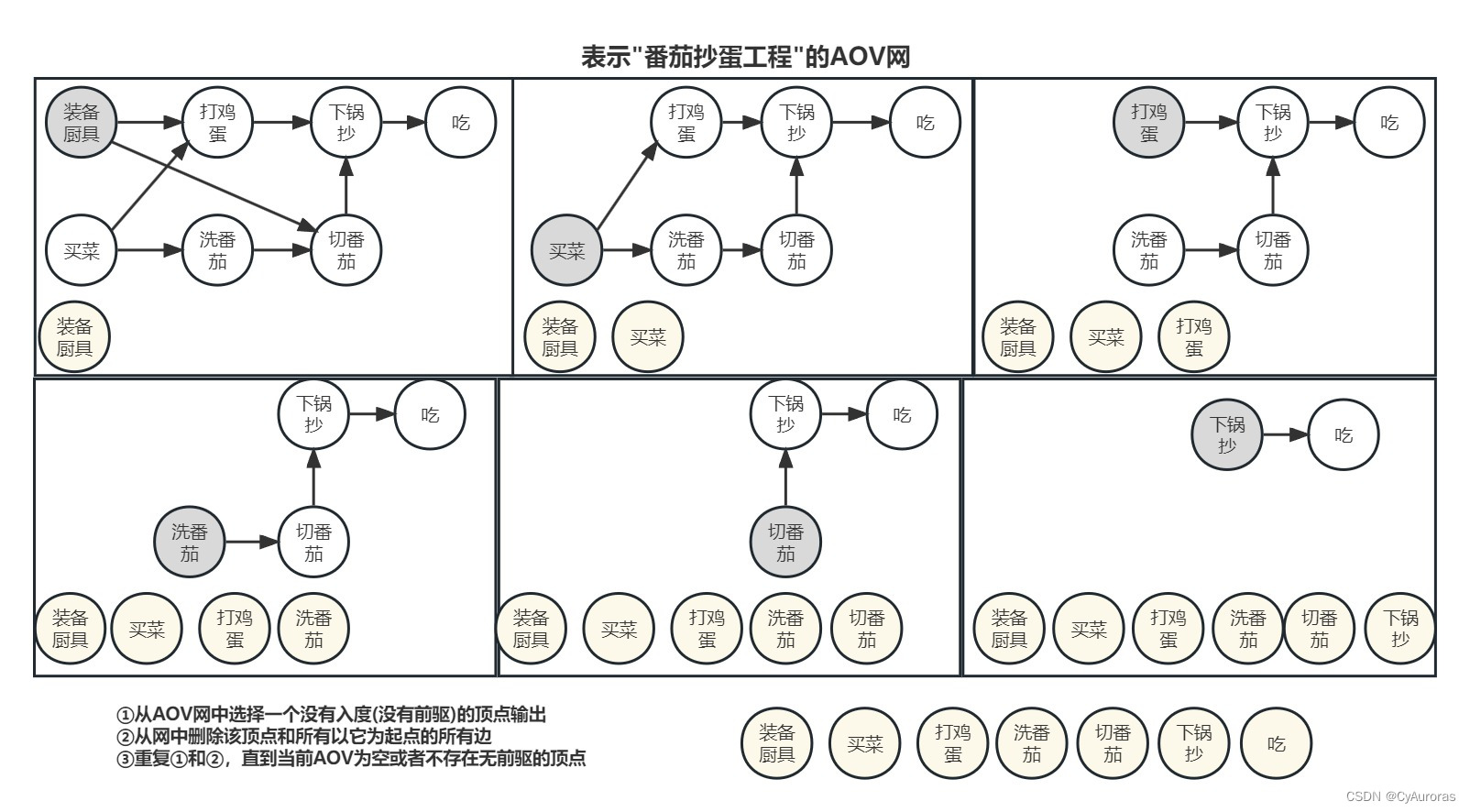
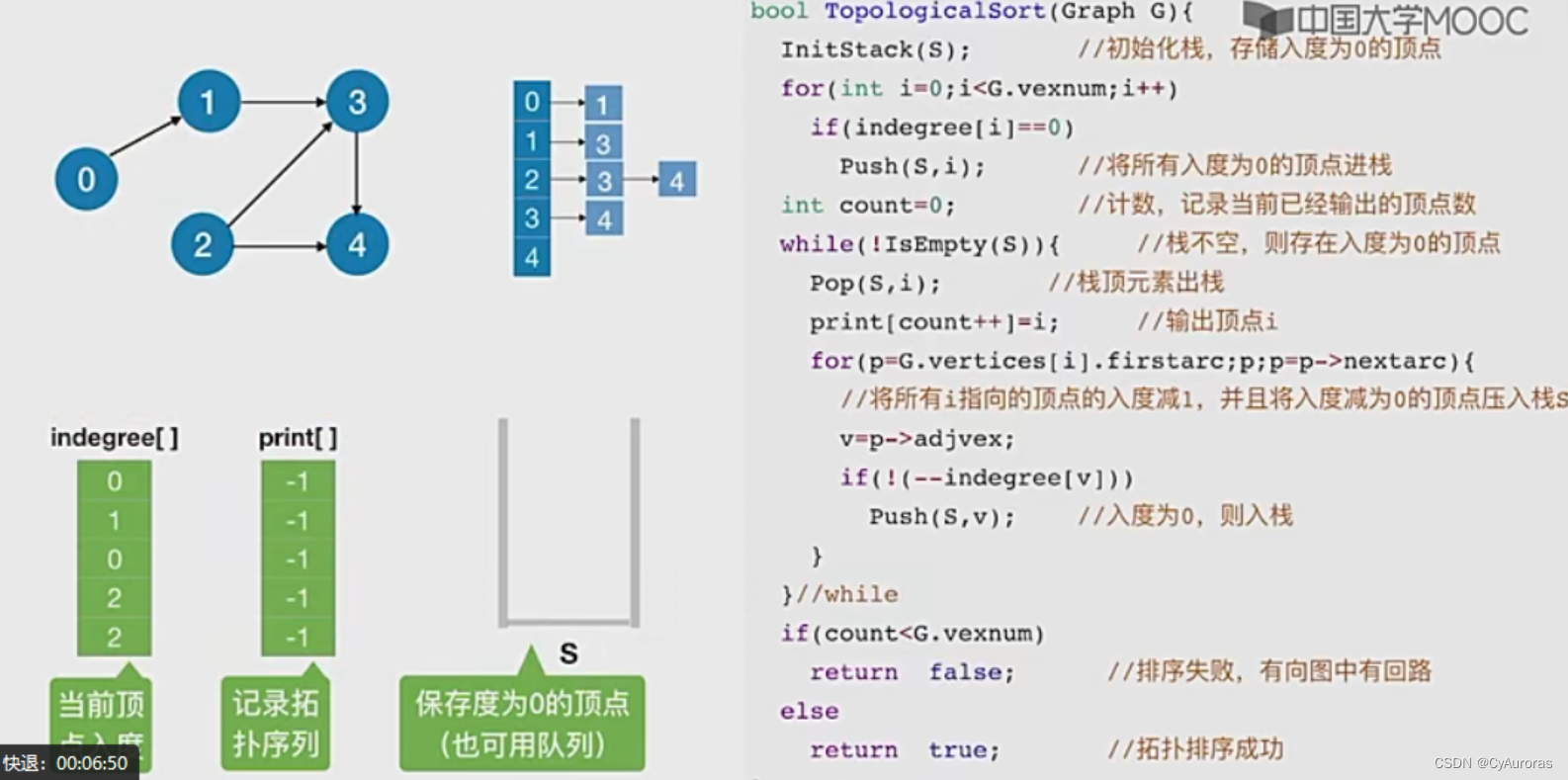
时间复杂度： $\tiny O(V+E)$

若采用邻接矩阵则 $\tiny O(V^2)$

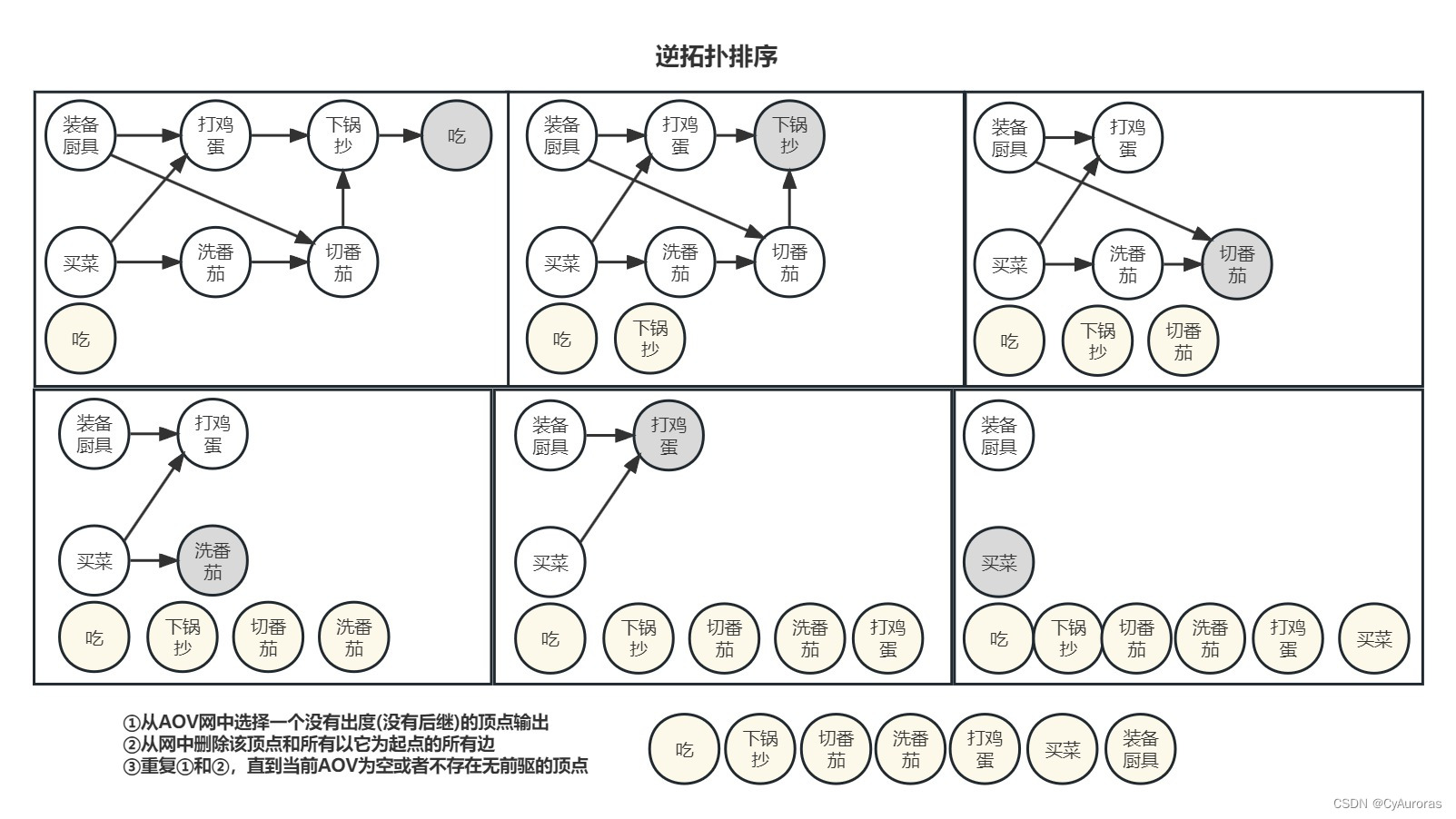
*逆拓扑排序

*2.5关键路径(AOE网)

在带权有向图中，以顶点表示事件，以有向边表示活动，以边上的权值表示完成该活动的开销(如时间)，称之为用边表示活动的网络，简称AOE网

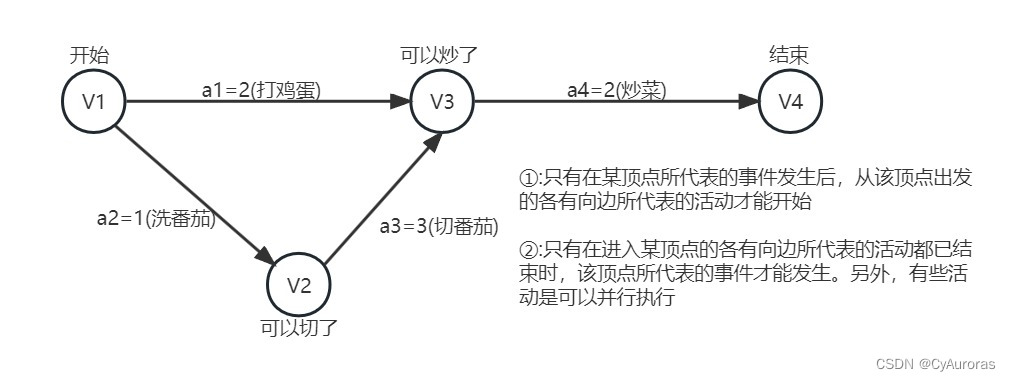
源点：AOE网仅有一个入度未0的顶点，称为开始顶点(源点),表示工程的开始。

汇点：也仅有一个出度为0的顶点，称结束顶点(汇点)，表示工程的结束

关键路径:从源点到汇点路径可能有多条，所有路径中，路径出度最大的为关键路径

事件(顶点) $\tiny v_k$ 最早发生时间 $\tiny ve(k)$ :决定了所有从 $\tiny v_k$ 开始的活动能够开工的最早时间

活动(边) $\tiny a_i$ 的最早开始时间 $\tiny e(i)$ :指该活动弧的起点所表示事件的最早发生时间

事件 $\tiny v_k$ 的最迟发生时间 $\tiny vl(k)$ :指不推迟整个工程前提下，事件最迟必选发生的时间 $\tiny e(i)=ve(k)$

活动(边) $\tiny a_i$ 的最迟开始时间 $\tiny l(i)$ ：指活动弧的终点所表示事件的最迟发生时间与该活动所需时间之差。 $\tiny l(i)=vl(i)-Weight(v_k,v_j)$

时间余量： $\tiny d(i)=l(i)-e(i)$