电子技术背后的数学本质【3】（放大器电路噪声的计算和去除）

这一篇我们主要对电路的噪声进行一个分析，尤其是在放大器电设计时，遇到的噪声问题。首先我们对噪声进行一个数学上的分析，得到噪声的表达式。然后对电路中常见的噪声进行一个分类，并根据之前的数学分析，给出计算噪声的方法。最后对于上述不同种类的噪声，提出一个抑制和去除的方法。

1.如何评价噪声——电能力和有效值

1.1什么是有效值和电能力

在对噪声进行分析之前，我们首先需要对“有效值”这一概念进行一个回顾。

我们在进行交流电的分析和表达的时候，往往遇到一个问题，那就是对于某些复杂的交流信号来说，我们希望对该交流电有一个描述，该描述能够某种程度上表达该交流电的能力。那么如何描述一个复杂的交流信号呢？

一种方法是，我们对该信号进行傅里叶变换，得到该信号在各个频率下的幅值大小，从而从中可以看出该交流信号的性能和特性。

这确实是一种十分科学并且详细的描述方式。但是如果所有的交流信号都需要这样描述，那就显得十分复杂，且不利于我们进行运算。所以我们需要寻求一种其他的描述方法。

如果我们对该交流信号的成分并不过多的关注，而是更看重该交流电的电能力，那可不可以用一个直流电，使该直流电和交流电具有相同的电能力，然后用直流电的参数来表示交流电的参数？

这就是有效值的来源。对于一个波动的电压u(t)，其大小随着时间的变化而变化。所以我们难以直接描述出该电压的大小。可是假设我们把该电压加到某阻性负载R两端时，电阻R会消耗功率发热，产生的热量为Q；如果我们用一个直流的电压U，加到相同的负载两端，能够产生相同的热量，那么我们可以用直流电压U来表示原波动电压u(t)的某种能力（例如让电阻发热的能力）。这里的U就是u(t)的电压有效值。

有以下公式推导：
波动电压的瞬时功率：
$$P(t)=\frac{u^2(t)}{R}$$
在一段时间内所产生的热量：
$$Q={\int }_0^T\frac{u^2(t)}{R}\mathrm{d}x$$
直流电压在相同的一段时间内所产生的热量：
$$Q=T\frac{U^2}{R}$$
若使两个热量相等，那么我们可以得到：
$$U_{rms}=\sqrt{\frac{1}{T}{\int }_0^T{u}^2(t)\mathrm{d}x}$$$$E_p=U^2=\frac{1}{T}{\int }_0^T{u}^2(t)\mathrm{d}x$$
这里，U就是波动电压的有效值，$E_p$就是波动电压的电能力。

可能有人就会有一个疑问，有效值的概念我们弄清楚了，也知道怎么来的了，为什么还要单独的给$U^2$起一个名叫“电能力”的名字？是不是多此一举呢？

当然，电能力的存在是有它深刻的科学依据的。下面来看：

1.2为什么要区分有效值和电能力

为什么要区分有效值和电能力呢？简单的概况是，对于独立信号来说，有效值不能叠加，电能力可以叠加。我们举一个简单的例子。

如果有两个相互独立的波动信号$u_1(t)$和$u_2(t)$，这两个信号叠加起来形成一个新的波动信号$u(t)$，那么这三者之间的电能力、有效值之间是个什么关系呢？

有以下推导：
在两个波动信号为正交信号的前提下
波动信号1的有效值：
$$U_{rms1}=\sqrt{\frac{1}{T}{\int }_0^T{u}_1^2(t)\mathrm{d}x}$$
波动信号1的电能力：
$$E_{p1}=\frac{1}{T}{\int }_0^T{u}_1^2(t)\mathrm{d}x$$
波动信号2的有效值：
$$U_{rms2}=\sqrt{\frac{1}{T}{\int }_0^T{u}_2^2(t)\mathrm{d}x}$$
波动信号2的电能力：
$$E_{p2}=\frac{1}{T}{\int }_0^T{u}_2^2(t)\mathrm{d}x$$
合成的波动信号的有效值：
$$U_{rms}=\sqrt{\frac{1}{T}{\int }_0^T{u}^2(t)\mathrm{d}x}=\sqrt{\frac{1}{T}{\int }_0^T(u_1(t)+u_2(t){)}^2\mathrm{d}x}$$$$=\sqrt{\frac{1}{T}{\int }_0^T(u_1^2(t)+u_2^2(t)+2u_1(t)u_2(t))\mathrm{d}x}$$若两个信号之间为正交信号，例如两个信号为频率不同的正弦信号，则两信号之间的乘积的积分为0，则原式可以化简为：
$$=\sqrt{\frac{1}{T}{\int }_0^T(u_1^2(t)+u_2^2(t){)}^2)\mathrm{d}x}=\sqrt{\frac{1}{T}{\int }_0^T{u}_1^2(t)\mathrm{d}x+\frac{1}{T}{\int }_0^T{u}_2^2(t)\mathrm{d}x}$$$$=\sqrt{U_{rms1}^2+U_{rms2}^2}$$
合成的波动信号的电能力：
$$E_p=\frac{1}{T}{\int }_0^T{u}^2(t)\mathrm{d}x=\frac{1}{T}{\int }_0^T(u_1(t)+u_2(t){)}^2(t)\mathrm{d}x$$$$=\frac{1}{T}{\int }_0^T(u_1^2(t)+u_2^2(t)+2u_1(t)u_2(t))\mathrm{d}x$$$$=\frac{1}{T}{\int }_0^T{u}_1^2(t)\mathrm{d}x+\frac{1}{T}{\int }_0^T{u}_2^2(t)\mathrm{d}x$$$$=E_{p2}+E_{p2}$$
总结来说：
$$E_p=E_{p2}+E_{p2}$$$$U_{rms}^2=U_{rms1}^2+U_{rms2}^2$$
我们可以看出，如果两个相互独立正交的波动信号叠加，实际上是其电能力的一个叠加，而不是其有效值的叠加。

并且，其实仔细品味我们在对有效值和电能力的定义，可以发现，实际上我们是要求交流和直流先有相同的电能力，再在相同的电能力情况下，取直流电此时的电压值作为交流电的电能力的表征值。因此有效值只是一个便于我们直观表述的量，而电能力才是我们真正想要表达的交流电的特征量。

电能力有时候也被认为是对于1Ω的电阻的电功率，因此某些时候我们说电功率其实实际上说的是电能力。

1.3噪声的有效值和电能力

我们已经知道了，对于一个波动信号，如何求其有效值和电能力。那么现在我们来看噪声信号。

首先我们说，对于一个电路，其中必定存在着噪声，噪声一般来说是一个不断变化的电信号，我们如果要对噪声进行描述，可以参考上述对波动信号的描述方法。

一种方法是采用傅里叶变换来进行描述。通过傅里叶变化，我们可以看出，噪声实际上是由不同频率、不同幅值的正弦信号叠加而成。我们通过频谱图，可以直观的看出，该噪声信号的构成。

但是上述这种表达方法，在有些时候下，并不能直观的表现出来，该噪声的大小。比如说，现在有两个噪声的频谱图，让我们判断两个噪声那个更大，那个对我们的正常信号影响更大。如果这两个图差别不大，可能我们无法直接判断出来。所以我们需要一些直观、简单的参数，来表示噪声的某些性能，以便于我们能够对噪声的大小、性能等进行一个评估。

那么我们也是可以采用有效值这一方法，来对噪声信号的大小进行一个评估。有效值大的噪声信号，我们认为其在较长的时间内，比有效值小的信号，其平均而言的电参数要大。我们可以简单的看出，我们更希望得到有效值为0.1V的噪声，而不是有效值为1V的噪声。

所以我们在噪声信号中，引入了有效值和电能力两个参数。但是如果我们采用相同的计算方法：

$$U_{rms}=\sqrt{\frac{1}{T}{\int }_0^T{u}^2(t)\mathrm{d}x}$$$$E_p=\frac{1}{T}{\int }_0^T{u}^2(t)\mathrm{d}x$$

这里就有一个问题，那就是，对于噪声来说，在一段时间内的值是不固定的，所以我们取一段时间内的噪声值，算它的有效值和电能力，结果可能不具有较高的代表性。可能我们一段时间内算出来一个有效值，另一段时间又会算出来另一个有效值。因此我们只有取时间无限长，才能得到一个稳定的有效值。

此外，如果我们要通过上式得到有效值和电能力，就需要先对一个已经存在的电路进行一段时间的采样。而往往我们需要在进行实际的电路设计之前就要对噪声进行一个估计。

总结来说，噪声也是一个波动信号，因此我们仍可以用电能力和有效值来对噪声进行评估。但是原来的有效值和电能力的计算方法并不适用于未知噪声的估计。因此我们需要寻找其他的计算有效值和电能力的方法。

1.4噪声的电能力密度

如何找到这种方法？

我们回到噪声的另一种表示方法，傅里叶的表示方法。我们发现，噪声实际上是无数个不同频率的正弦信号的组合，我们知道，不同频率的正弦信号相互之间是正交的，而相互正交的波动信号的电能力是可以叠加的。那么我们就能想到，如果对于一个噪声信号，我们把其组成成分中所有频率的正弦信号找到，求每一个正弦信号的电能力，再将其电能力叠加起来，就是整个噪声的电能力。（这也就是为什么我们之前要尤其强调电能力能够叠加这一问题）

通过这种方法，我们从频域入手，避开了时域上的问题。也就是说，此时我们将原来的时域上的噪声信号$u(t)$，拿到了频率域$u(f)$上去分析。

（这里对于时域和频率域之间的关系，我在之前的《信号完整性分析笔记》一篇中，有一些介绍）

因此这里我们引入一个新的概念，那就是电能力密度，即$f_a$频率正弦波所具有的电能力，符号为$D_E(f_a)$，其单位为$V^2/Hz$。

那么我们已知某噪声信号在所有频率下的电能力密度，通过积分就能得到该噪声的总的电能力：
$$E_p={\int }_0^{\infty }{D}_E(f)\mathrm{d}f$$
通过这个式子，我们在估计噪声的时候，就不用实地进行某一段时间的实验和测量来求得电能力，而只需要知道某噪声信号的电能力随频率变化的曲线——电能力密度曲线。电能力密度曲线的横轴为频率，单位为Hz，纵轴为电能力密度，单位为$V^2/Hz$。这样我们对电能力密度曲线在频率上积分就能得到总的电能力，从而开根号得到有效值。

而电能力密度曲线对于常见的噪声种类例如电阻热噪声，或对于市面上已有的电子产品，都是有相应的计算公式或者厂家已经给出的电能力密度曲线。这就让我们估计电路的噪声有了计算的依据。

1.5其他密度曲线

除了电能力密度以外，科学家们还定义了其他的密度曲线，例如：

电压密度，单位为$V/\sqrt{Hz}$，是电能力密度的开方。和电能力密度是同源的，知其一就能算出另一个。

功率谱密度，单位为$W/Hz$，可以理解为单位电阻所承载的电能力。

等等，理解起来和电能力密度相似，所以我们并不细说，用的时候再仔细说一下。

1.6噪声的有效值和峰峰值之间的关系

我们可以通过有效值来判断两个噪声之间那个噪声水平较低，但是我们在进行示波器测量的时候，是无法直接看出来当前噪声的有效值大小的。但是我们可以通过示波器简单的找到当前噪声的峰峰值。

此外我们在进行噪声电路设计的时候，可能对于噪声的峰值更加关注，尤其是对于AD转换电路或者比较触发电路等。因此我们需要得到一个峰峰值和有效值之间的关系。

噪声是符合统计学规律的，在正态分布中，在$\pm 3\sigma$范围内发生的概率为99.9%，所以我们可以认为噪声的有效值和峰峰值之间的关系为：
$$U_{N-pp}=6.6U_{N-rms}$$

即峰峰值为有效值的6.6倍。

2.电路内部产生的噪声

对于我们设计的电路，其噪声来源大的方面来说，可以分为以下两类，一类是电路内部产生的噪声。一类是由外部电路引入的干扰。首先我们先看电路内部产生的噪声。

电路内部产生的噪声，我们又可以按照不同的方法进行分类。一种方法是根据该噪声的电能力密度曲线的形式来分类；另一种方法是根据噪声产生的来源来进行分类。

2.1从波形上看——白噪声和1/f噪声

白噪声又称平坦噪声。其电能力密度曲线为一条直线，也就是说，这种噪声的电能力与频率无关，在各个频率上均匀分布。因此此时的电能力密度相对于频率，是一个常数。
假设该常数为：
$$D_E(f)=K^2$$

根据我们之前的公式，可以得到，在某一频率范围内（$f_a-f_b$），该噪声的电能力为：
$$E_p={\int }_{f_a}^{f_b}{K}^2\mathrm{d}f=K^2(f_b-f_a)$$

该噪声的有效值为：
$$U_{rms}=K\sqrt{f_b-f_a}$$

另一种噪声为1/f噪声，其电能力密度曲线随着频率的增加而下降。且其电能力密度与频率的导数成正比关系。也就是说，该噪声的电能力密度为：
$$D_E(f)=C^2\frac{1}{f}$$

同样我们可以得到该噪声在某一频率范围内的电能力：
$$E_p={\int }_{f_a}^{f_b}{C}^2\frac{1}{f}\mathrm{d}f=C^2\ln \frac{f_b}{f_a}$$

以及该噪声在某一频率范围内的有效值：
$$U_{rms}=C\sqrt{\ln \frac{f_b}{f_a}}$$

2.2噪声计算中系数K和C的确定

如果要计算总的噪声有效值，我们需要知道系数，还需要知道频率范围，这样才能算出来一个具体的噪声值。首先我们先看如何确定系数。

如果已知噪声的总的电能力密度曲线（或电压密度曲线），这种密度曲线一般来说是类似于1/f噪声和白噪声的组合，那么我们通过一些方法把这种混合的电能力密度曲线分解成单独的1/f噪声和白噪声，并得到两种形式的噪声的系数值。

举例来说明：

如下图所示，是常见器件的噪声的电压密度曲线。可以看到，这种曲线有这样的特征，低频段以1/f噪声为主，并且随着频率的上升而下降，最终1/f噪声几乎不存在，而呈现出平坦的白噪声的波形。

那么通过波形分类的方法，我们如何来分析噪声大小呢？

仔细观察之前所说的1/f噪声和白噪声的计算公式，我们可以看到，在某频率范围内的噪声大小，与频率范围以及系数K或者系数C有关。因此对于求噪声的大小的问题，实际上就是确定系数大小和频率范围的问题。

对于系数值，我们分别来说。对于平坦噪声，我们取频率最高的那一点处的值为K值。上图可以看出，此时的K值约为$9nV/\sqrt{Hz}$。所以K值就能得到了。除了看图，在很多元件的数据手册中，也会给出在高频率下的噪声电压密度值，该值也是K值。所以我们可以通过看图或者查表，十分容易的得到K的大小。

对于1/f噪声来说，如果曲线包含了1Hz处的噪声电压密度，那么我们知道，C为1Hz处1/f噪声的电压密度值，而该曲线在1Hz处的噪声是1/f噪声和白噪声的叠加，因此假设当前1Hz处的噪声电压密度为D，则有：
$$D^2=C^2+K^2$$

我们已经得到K的大小，因此简单计算，就能得到：
$$C=\sqrt{D^2-K^2}$$

这里，我们看图可知，D约为$50nV/\sqrt{Hz}$，K约为$9nV/\sqrt{Hz}$，则计算可得C约为$49.1nV/\sqrt{Hz}$。
可是如果在曲线中没有包含1Hz处的噪声电压密度，怎么求C的大小呢？
我们取频率最小的点$f_{min}$处的噪声电压密度$D(f_{min})$来计算。
$$D(f_{min}{)}^2=C(f_{min}{)}^2+K^2=C^2\frac{1}{f_{min}}+K^2$$

$$C=\sqrt{\frac{f_{min}}{1}(D(f_{min}{)}^2-K^2)}$$

例如我们取3Hz处的值来计算，$D(3Hz)=23nV/\sqrt{Hz}$，$K=9nV/\sqrt{Hz}$，则：
$$C=\sqrt{\frac{3}{1}(23^2-9^2)}=36.7nV/\sqrt{Hz}$$

这样我们也能够得到C的大小。不过细心的同学可能发现，这两次得到的C值不一致。其实这是因为我们把曲线简化成了1/f和白噪声的叠加，但实际的器件往往并不是一个完美的1/f噪声曲线和白噪声的叠加。因此我们在简化过程中引入了误差，不过由于1/f噪声的频率范围比较窄，因此有些许误差并不对总的噪声水平有太大的影响（上图为对数坐标图，因此低频段的坐标长度被拉大，高频段的坐标长度被压缩，如果我们采用线性坐标图，就能发现，实际上1/f噪声仅仅在20Hz范围内存在，而白噪声在10KHz范围内都存在，因此最终的积分结果是，1/f噪声对总的噪声的影响力远小于白噪声）。

2.3噪声计算中频率上下限$f_a$和$f_b$的确定

我们要计算噪声的有效值，除了已知系数K和C之外，还需要已知频率的上下限，那么接下来我们就探讨一下如何确定噪声的上下限。

首先对于白噪声，一般来说，白噪声的频率上限要远远大于频率下限，因此有以下公式：
$$U_{rms}=K\sqrt{f_b-f_a}=K\sqrt{f_b}$$

因此白噪声只需要知道频率上限即可。

如何确定白噪声的频率上限呢？我们知道白噪声在无穷大的频率上都是存在的，难道我们的积分上限为无穷大吗？如果是无穷大，这种积分算下来的值也是无穷，这样就无法表示白噪声的电能力和有效值了。

我们在数学中讨论这个问题，确实会遇到积分上限无穷大的现象。但是幸运的是，噪声是一个存在于真实世界中的东西，所以噪声必定存在于某种电路之中。而任意一个电路，都有一个带宽（关于带宽的描述我在《信号完整性分析》读书笔记中有过描述）。因此带宽上限的存在，使得噪声在超过带宽上限后会快速衰减，这样我们在积分的时候，可以认为在超过某个频率之后，噪声的衰减十分大，因此之后的积分都为0，这个频率就是频率上限。

这里我们注意一个改变，之前说噪声我们都是单独对其进行分析，但是在这里，我们将噪声分析放在了一个具体的电路中。这就为噪声引入了新的影响。我们知道，任何一个电路对于其输入信号都有一个增益的影响，最终表现为一种输出，例如RC滤波电路，这种信号输入、电路、信号输出的关系，我们在上一篇中进行了十分详细的说明。这里对于噪声，也是如此，只是信号输入为噪声，在电路的增益下，我们研究噪声的输出。这样就引入了一个噪声增益的问题，我们设噪声增益为：$A_n(j\omega )$或$|A_n(jf)|$，这里噪声增益就是我们之前的系统的增益，只是我们在傅里叶域中讨论，就有一个频率和相位和增益三者的关系，所以是以上的性质，其本质如我们在上一篇所说，都是系统本质的一种表现。

那么我们有，输入噪声密度和输出噪声密度之间的关系：
$$u_{n-out}(f)=|A_n(jf)|u_{n-in}(f)$$

那么我们之前所说的有效值的计算公式也变为：
$$U_{rms}=\sqrt{{\int }_0^{\infty }{u}_{n-out}^2(f)\mathrm{d}f}=\sqrt{{\int }_0^{\infty }|A_n(jf){|}^2{u}_{n-in}^2(f)\mathrm{d}f}$$

那么回到我们所说的上限频率的问题，如果我们所在的电路是一个RC低通滤波器，那么如何利用上式，得到系统的上限频率，进而得到整个噪声的有效值$U_{r}ms$？

我们知道，RC低通滤波器的系统增益为：
$$A_n(j\omega )=\frac{1}{1+j\omega RC}$$

设$f_0=\frac{1}{2\pi RC}$，则有
$$A_n(jf)=\frac{1}{1+j\frac{f}{f_0}}$$

$$|A_n(jf){|}^2=|\frac{1}{1+j\frac{f}{f_0}}{|}^2=\frac{1}{1+(f/f_0{)}^2}$$

那么，对于输入为K的白噪声来说，输出的噪声的有效值为：
$$U_{rms}=\sqrt{{\int }_0^{\infty }|A_n(jf){|}^2{u}_{n-in}^2(f)\mathrm{d}f}$$$$=\sqrt{{\int }_0^{\infty }\frac{1}{1+(f/f_0{)}^2}{K}^2\mathrm{d}f}$$$$=K\sqrt{{\int }_0^{\infty }\frac{1}{1+(f/f_0{)}^2}\mathrm{d}f}$$$$=K\sqrt{\frac{\pi }{2}{f}_0}=K\sqrt{1.57f_0}$$

比较一下我们之前的公式
$$U_{rms}=K\sqrt{f_b-f_a}=K\sqrt{f_b}$$

可以看出，对于RC低通滤波器电路，我们的上限频率就是$1.57f_0$

这里不仅仅是得到一个上限频率，更重要的是，我们关注的噪声从输入信号，经过了系统，变成了输出信号。我们真正关心的实际上是系统的输出噪声的有效值，这个值才是实际存在的值。

这里我们可以看出，对于不同的系统，其增益不同，最后的上限频率也不同，例如一阶低通滤波器，$f_b=1.57f_0$；二阶低通滤波器，$f_b=1.11f_0$；三阶低通滤波器，$f_b=1.05f_0$。可见阶数越高，上限频率越接近于$f_0$。

常见的系统一般来说都可以找到这个$f_0$，一般来说为系统的-3dB频率，然后我们再根据系统的阶数来确定$f_b$。例如，对于运算放大器来说，$f_0=F\times GBW$，F为反馈系数，GBW为单位带宽增益。

对于复杂系统来说，我们需要对噪声增益进行具体和详细的分析，才能得到最终的输出噪声的有效值。这一部分我们在最后会详细介绍。

然后我们来看1/f噪声，对于1/f噪声，有
$$U_{rms}=C\sqrt{\ln \frac{f_b}{f_a}}$$

可以看出，我们的频率下限$f_a$不能取0，否则算式也是无穷的。那么这个值我们一般取0.1Hz，因为工程上认为，低于0.1Hz的噪声，一般可以认为是人造成的，与电路本身无关。

而频率上限$f_b$取1/f的转折处频率即可，这里频率上限的取值实际上对结果影响不大，因为这里经过一次ln对数化，又经过了开放，因此即使$f_b$取大了，最终的结果也不会变化很大。

2.4从来源上看——电阻的热噪声和三极管的噪声

任何电阻（导体）即使不与电源接通，其两端也存在电压，这是由于导体内部自由电子随机的热运动造成的。在某一个瞬时，一个方向运动的电子数目大于另一个方向运动的电子数目，这就造成了随机的电压的产生。这种由于电子随机热运动而产生的随时间变化的电压称为热噪声电压。

纯电抗元件没有热噪声。（现实中不存在纯电抗元件，但是数学中存在）

那么我们有公式可以得到，热噪声的电能力密度和电压密度分别为：
$$D_E(f)=4kTR$$$$V/\sqrt{B}=\sqrt{4kTR}$$

其中k为玻尔兹曼常数，其值为$1.38\times 10^{-23}J/K$，T是热力学温度，单位是K，R为电阻，单位是Ω。

可以看出，电阻热噪声是一种白噪声。其电能力密度和电压密度和频率无关。

电阻热噪声的大小和阻值有关，阻值越大，噪声的电能力密度和电压密度越大。

三极管的噪声较电阻的噪声复杂，主要有热噪声、散粒噪声、闪烁噪声、雪崩噪声等。其中散粒噪声为白噪声，闪烁噪声为1/f噪声。

上述噪声的具体表达式这里就不给出了，但是需要知道的是，三极管的噪声随着通过PN结的电流的增大而增大。

3.复杂电路噪声计算实例

这里我们以一个复杂电路的噪声计算为例，来感受一下一个真正严谨的噪声运算的过程，以及对我们上述知识进行一个运用。

关注噪声的一个重要应用就是光电二极管放大器电路。该电路常常采用电流—电压转换模式的运算放大器电路，该电路的模型如下：

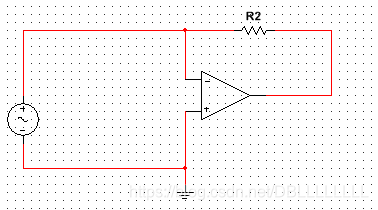
该输入信号为电流源。通过如图所示的电路图，将十分微弱的小电流信号（一般为uA甚至pA级的信号）放大到mV或者V级，因此对于这种小电流信号，噪声的影响十分关键。这里就需要对该电路的噪声水平进行一个分析。

由于光电二极管中存在寄生电阻和寄生电容，反馈电阻也存在着杂散电容，以及我们之前所说的放大器的其他噪声，因此我们需要对上图电路进行一定的等效。

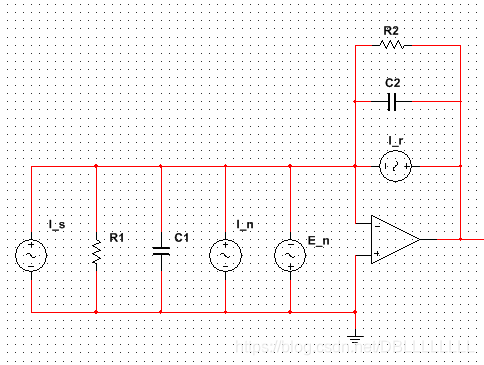
如图所示为等效后的噪声模型。其中$R_1$为光电二极管的寄生电阻，$C_1$为光电二极管的寄生电容，$R_2$为放大器的反馈电阻，$C_2$为反馈电阻的杂散电容。$I_n$为输入噪声电流，$E_n$为输入噪声电压，$I_r$为电阻热噪声。

那么我们来分析一下该电路的噪声。

3.1输入噪声电流$I_n$的输出噪声谱密度

首先我们先分析简单的输入噪声电流。

输入噪声电流$I_n$主要是输入偏置电流$I_B$的散粒噪声，其噪声密度有公式可用：

$$I_n=\sqrt{2q{I}_B}$$

这里，q为电子所带电荷量，为$1.6\times 10^{-19}$C。

该输入电流噪声引起的噪声电压$E_{noi}$为：

$$E_{noi}=R_2{I}_n=R_2\sqrt{2q{I}_B}$$

一般来说，输入电流噪声的噪声密度值比较小，假设已知输入偏置电流$I_B$=25nA，反馈电阻为$R_2$=100KΩ，则$E_{noi}=8.94nV/\sqrt{Hz}$。

3.2电阻输入噪声电流$I_r$的输出噪声谱密度

电阻输入噪声的噪声谱密度，可以直接根据我们上述所说的，电阻热噪声的公式来求得，这里我们直接求出在输出端的电阻热噪声：

$$E_{nor}=\sqrt{4KT{R}_2}$$

已知反馈电阻为$R_2$=100KΩ，波尔茨曼常数K=$1.38\times 10^{-23}$，热力学温度T=298，则$E_{nor}=40.5nV/\sqrt{Hz}$

3.3输入噪声电压$E_n$的输出噪声谱密度

最后我们来看输入噪声电压$E_n$所造成的输出噪声谱密度。因为放大器会对输入噪声电压放大，因此该关系会比较的复杂。所以这里，我们的思路是，已知输入噪声电压的情况下，根据放大器电路，求出噪声增益曲线，从而得到了该部分引起的输出电压噪声噪声密度和频率之间的曲线，再对曲线各部分进行积分，从而得到总的噪声功率（或有效值）。

首先，放大器的输入噪声电压的噪声谱密度一般来说是由运放的使用手册给出。如下图。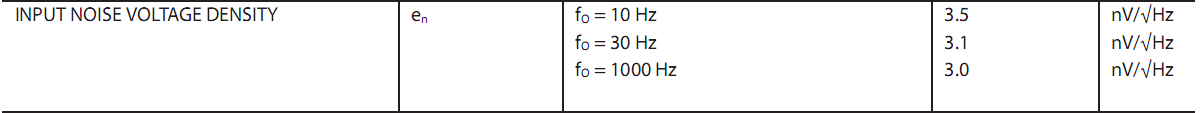

那么我们需要做的就是根据电路图求出噪声增益曲线。

通过上一篇的讲解，我们知道了对于运算放大器来说，其闭环增益约为反馈系数的倒数，这里在噪声增益这里也是适用的。我们有以下公式：
$$噪声增益A_n=\frac{1}{F}$$

$$反馈系数F=\frac{Z_1}{Z_1+Z_2}=\frac{R_1||\frac{1}{j2\pi f{C}_1}}{R_1||\frac{1}{j2\pi f{C}_1}+R_2||\frac{1}{j2\pi f{C}_2}}$$

化简得：
$$噪声增益A_n=\frac{1}{F}=(1+\frac{R_2}{R_1})\frac{1+j2\pi f{R}_2{C}_2}{1+j2\pi f(R_1||R_2)(C_1+C_2)}$$

设：
$$f_p=\frac{1}{2\pi R_2{C}_2}$$

$$f_z=\frac{1}{2\pi (R_1||R_2)(C_1+C_2)}$$

则
$$\frac{1}{F}=(1+\frac{R_2}{R_1})\frac{1+j\frac{f}{f_z}}{1+j\frac{f}{f_p}}$$

可以看出，该增益为积分环节和微分环节的组合，且各环节的转折频率之间的关系为$f_z<f_p$，且在低频段的时候$\frac{1}{F}=1+\frac{R_2}{R_1}=1$（$R_2>>R_1$），在高频段的时候$\frac{1}{F}=1+\frac{C_1}{C_2}$。

因此曲线的图像为，开始为直线$1+\frac{R_2}{R_1}$，在$f_z$处向上转折45度，再在$f_p$处向下转折45度，然后曲线为直线$1+\frac{C_1}{C_2}$。

当增益达到开环增益时，如果没有开环增益的限制，曲线会保持直线，但是由于存在开环增益的限制，曲线在交叉频率$f_x$处产生滚降。根据单位增益带宽$f_t$的定义，我们有以下等式：

$$f_x\times \frac{1}{F}=f_t$$

$$f_x=f_t\times F=\frac{C_2}{C_1+C_2}{f}_t$$

总结来说，最终的曲线有三个拐点，拐点处的频率分别为：$f_z$，$f_p$，$f_x$。

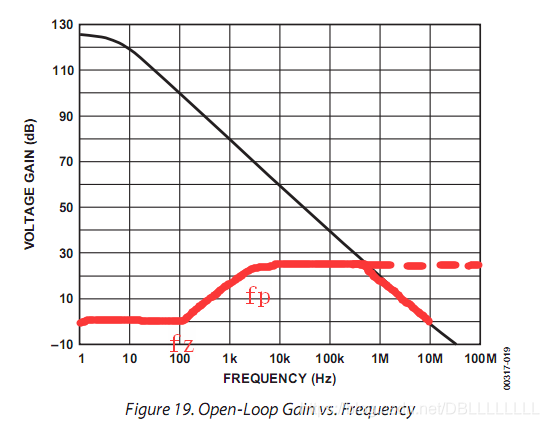
因此，噪声的增益为：

$$A_n=(1+\frac{R_2}{R_1})\frac{1+jf/f_z}{(1+jf/f_p)(1+jf/f_x)}$$

因此，该部分噪声最终得到的输出噪声的密度为：

$$E_{noe}(f)=A_n(f)E_n$$

3.4已知电阻噪声和电流噪声的输出噪声谱密度求输出噪声的有效值

到这里我们已经求出来了三个不同噪声源所产生的对应的输出电压噪声谱密度，我们需要知道的是，该噪声谱密度最终得到的噪声的总功率和有效值是多少。

通过上文的学习，我们知道了，只需要对噪声谱密度在所需频率范围内进行积分即可。但是频率范围不能是无限大的，因此我们需要得到噪声积分的频率范围。

参考之前所说的把电路看做一阶滤波系统从而得到积分的带宽，这里我们也是采用这种思想，来实现对放大器电路的积分。下面我们就具体说明如何确定积分的带宽。

首先对于电流噪声和电阻噪声，其经过了放大器反馈电路，而放大器反馈电路若将其看做是一个一阶滤波电路的话，其信号在某个频率处存在一个滚降，该频率$f_{b0}$为：

$$f_{b0}=\frac{1}{2\pi R_2(C_1+C_2)}$$

那么把该一阶滤波电路再进一步抽象，看做是理想的滤波器，那么最终我们得到的频率上限$f_b$为：
$$f_b=1.57f_{b0}=\frac{1}{2\pi R_2(C_1+C_2)}=\frac{1}{4R_2(C_1+C_2)}$$

我们知道，对于功率谱密度为常数的噪声，我们的计算方法是：

$$U_{rms}=K\sqrt{f_b-f_a}=K\sqrt{f_b}$$

因此，我们可以算出电阻热噪声的输出电压的有效值：

$$U_{nor}=\sqrt{4KT{R}_2{f}_b}=\sqrt{\frac{KT}{C_1+C_2}}$$

以及电流噪声的输出电压的有效值：

$$U_{noi}=R_2\sqrt{2q{I}_B{f}_b}=\sqrt{\frac{q{I}_B{R}_2}{2(C_1+C_2)}}$$

3.5已知电压噪声的噪声增益求输出噪声的有效值

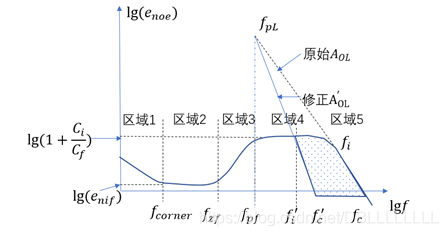
对于电压噪声来说，有所不同，因为电压噪声不能简单的看做常数型噪声，也不是1/f类型的噪声，而是复杂形状的噪声曲线。因此我们需要对该曲线进行分段积分再求和，才能得到总的输出噪声的有效值。

根据上文的分析，我们已知：

噪声增益为：

再从数据手册中得到输入电压噪声的电压谱曲线图：

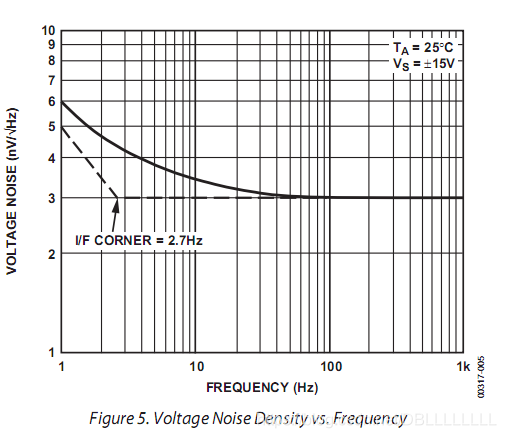
那么我们的输出噪声谱密度曲线是上面两个曲线的叠加：

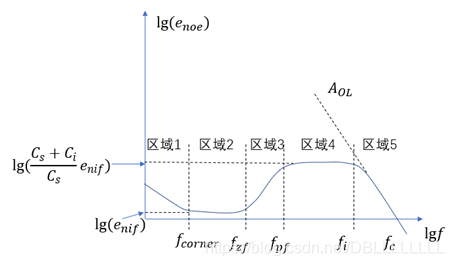
通过这个曲线，我们可以分别计算上述五个区域的电能力，然后相加得到总的电能力，从而得到总的输出电压噪声的有效值。

那么我们分别来计算各个区域的电能力和有效值：

对于区域一：

是一个1/f噪声，这里取积分下限为0.1Hz或0.01Hz即可，积分上限取转角频率$f_{corner}$即可。且在低频段所以这一部分的噪声电压的有效值为：
$$U_{noe1}=\sqrt{[(1+\frac{R_2}{R_1})E_n{]}^2{f}_{corner}\ln \frac{f_{corner}}{0.1Hz}}$$$$=(1+\frac{R_2}{R_1})E_n\sqrt{f_{corner}\ln \frac{f_{corner}}{0.1Hz}}$$

对于区域二：

这一部分为常数的噪声曲线，因此有：
$$U_{noe2}=\sqrt{[(1+\frac{R_2}{R_1})E_n{]}^2(f_{zf}-f_{corner})}$$$$=(1+\frac{R_2}{R_1})E_n\sqrt{f_{zf}-f_{corner}}$$

对于区域三：

这一部分的噪声曲线在对数上是以某个斜率直线上升的，因此有：
$$U_{noe3}=\frac{E_n}{f_{zf}}\sqrt{\frac{f_{pf}^3-f_{zf}^3}{3}}$$

这里，
$$f_{pf}=\frac{1}{2\pi R_2{C}_2}$$

$$f_{zf}=\frac{1}{2\pi (R_1||R_2)(C_1+C_2)}$$

对于区域四：

这一部分的噪声也是常数型额定，因此有：

$$U_{noe4}=(1+\frac{C_1}{C_2})E_n\sqrt{f_i-f_{pf}}$$

这里，$f_i$就是我们上述的交点频率，因此有：
$$f_i=f_c\times F=\frac{C_2}{C_1+C_2}{f}_c$$

对于区域五：

该部分的噪声，也是一个对数直线型的噪声曲线，因此有：
$$U_{noe5}=E_n{f}_c\sqrt{\frac{1}{f_i}}$$

那么总的输出噪声电压的有效值为上述各部分有效值的平方和：
$$U_{noe}=\sqrt{U_{noe1}^2+U_{noe2}^2+U_{noe3}^2+U_{noe4}^2+U_{noe5}^2}$$

（这里如果通过计算发现$f_{zf}$小于$f_{corner}$，这就表明上述的区域2不存在，曲线没有这一段平坦区域，那么这里计算的时候将区域2的电压的有效值视为0即可）

3.6总输出电压噪声的有效值计算

总的输出电压噪声的有效值为上述三个噪声有效值的平方和:

$$U_{no}=\sqrt{U_{nor}^2+U_{noi}^2+U_{noe}^2}$$

有了有效值，我们可以估计出噪声的峰峰值为：

$$U_{pp}=6.6U_{no}$$

4.复杂电路噪声降噪处理

在实际电路中，我们通过上述的计算，很有可能得到的噪声水平较大，这时就需要我们对电路进行一些降噪处理。

我们通过计算可以看出，噪声的主要部分是输入电压噪声和噪声增益所产生的这一部分噪声，这这一部分噪声中，又以区域3、区域4、区域5为主要贡献区域。因此我们主要把目光集中在这几个区域。

因此我们有以下思路：

降低区域3的带宽，也就是将$f_{zf}$向右移。

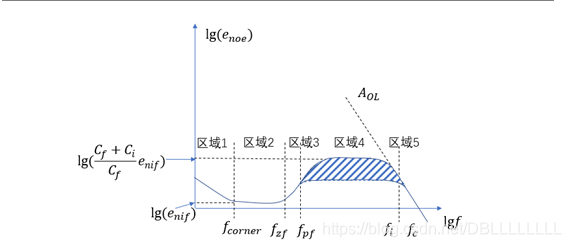
降低区域4的增益幅度。可以通过增加反馈电容来实现：

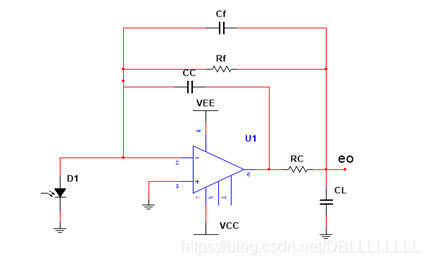
降低区域5的带宽，也就是将$f_c$向左移。可以通过相位补偿来实现：