1.运放噪声模型
运放构成的同相放大器的噪声模型如下
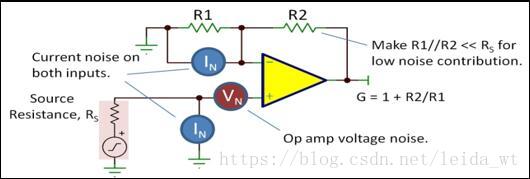
运放的噪声主要由三部分组成,运放电压噪声,运放电流噪声,和反馈电阻产生的热噪声。三者有效值的平方和再开根号就是总噪声的有效值。现代运放的电流噪声非常小,通常可以忽略不计。这些噪声经过放大器放大后出现在运放的输出中,放大系数称噪声增益。同相放大中,噪声增益和运放的信号增益都是
G
=
1
+
R
2
/
R
1
G=1+R_2/R_1
G=1+R2/R1,但在反相放大中,噪声信号的路径仍是同相放大,
G
=
1
+
R
2
/
R
1
G=1+R_2/R_1
G=1+R2/R1,不等于信号增益。
2.运放噪声基础
有效值(RMS): 有效值是根据电流热效应来规定的,又称均方根值。
RMS
=
1
n
(
x
1
2
+
x
2
2
+
⋯
+
x
n
2
)
RMS
=
1
T
2
−
T
1
∫
T
1
T
2
[
f
(
t
)
]
2
d
t
\text{RMS}=\sqrt{\frac{1}{n}(x_1^2+x_2^2+\cdots +x_n^2)}\\ \text{RMS}=\sqrt{\frac{1}{T_2-T_1}\int_{T_1}^{T_2}[f(t)]^2dt}\\
RMS=n1(x12+x22+⋯+xn2)RMS=T2−T11∫T1T2[f(t)]2dt
噪声叠加原理:

即,有效值的平方具有线性可加性,因此可记
E
p
=
U
N
2
E_p=U_N^2
Ep=UN2,则
E
p
=
E
p
1
+
E
p
2
E_p=E_{p1}+E_{p2}
Ep=Ep1+Ep2。
引入
D
E
(
f
)
=
lim
Δ
f
→
0
E
p
Δ
f
D_E(f)=\lim_{\Delta f\to0}\frac{E_p}{\Delta f}
DE(f)=limΔf→0ΔfEp描述单位频率内噪声的大小,即噪声在各个频率处的分布密度,单位
n
V
2
/
Hz
nV^2/\text{Hz}
nV2/Hz,而
D
U
(
f
)
=
D
E
(
f
)
D_U(f)=\sqrt{D_E(f)}
DU(f)=DE(f)称为噪声电压密度,单位
n
V
/
Hz
nV/\sqrt{\text{Hz}}
nV/Hz,数据手册中给出的就是此值。由噪声的叠加原理,要计算某一频率区间内的噪声总值只需对噪声密度积分即可。
频段内噪声有效值
(
R
M
S
)
=
E
P
=
∫
f
a
f
b
D
E
(
f
)
d
f
=
∫
f
a
f
b
D
U
2
(
f
)
d
f
频段内噪声有效值(RMS)=\sqrt{E_P}=\sqrt{\int_{f_a}^{f_b}D_E(f)df}=\sqrt{\int_{f_a}^{f_b}D_U^2(f)df}
频段内噪声有效值(RMS)=EP=∫fafbDE(f)df=∫fafbDU2(f)df
噪声的RMS值再乘6就是噪声峰峰值,这个系数6来自高斯分布的
6
σ
6\sigma
6σ。
运放的噪声特性:
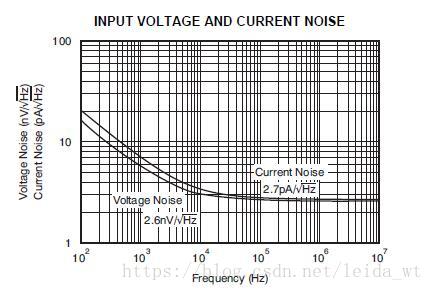
在器件的数据手册中,运放的噪声信息以噪声密度图的形式给出(如上图)即噪声的频谱。曲线分两个区间:闪烁噪声和宽白噪声。
(1)前面随着频率下降的部分称为闪烁噪声(flicker noise, 1/f 噪声),表达式是
D
E
(
f
)
=
C
2
f
D_E(f)=\frac{C^2}{f}
DE(f)=fC2,C是归一化到1Hz处的1/f噪声电压密度,
C
=
e
n
f
∗
f
0
C=e_nf*\sqrt{f_0}
C=enf∗f0。
e
n
f
e_{nf}
enf是1/f噪声频谱图上最小频率处噪声值,
f
0
f_0
f0是1/f噪声频谱图上最小频率。
(2)曲线后面平直部分称为宽白噪声,表达式是
D
E
(
f
)
=
K
2
D_E(f)=K^2
DE(f)=K2,K为白噪声电压密度。
对此频谱积分得到1/f噪声和白噪声RMS值分别为
C
⋅
ln
f
a
f
b
C\cdot \sqrt{\ln \frac{f_a}{f_b}}
C⋅lnfbfa和
K
f
b
−
f
a
K\sqrt{f_b-f_a}
Kfb−fa。
其中积分下界
f
a
f_a
fa一般取0.1,低于这个频率的噪声一般认为是外界扰动(如温度变化),不再被考虑到电路噪声中。积分上界
f
b
f_b
fb的近似计算公式为
f
b
=
k
增益带宽积
电路闭环增益
f_b=k\frac{增益带宽积}{电路闭环增益}
fb=k电路闭环增益增益带宽积。式中k为经验修正系数,它是由运放的低通效应引起的。普通放大器看做一个一阶滤波器,系数取1.57即可。
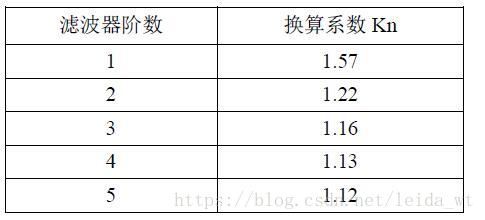
电阻的热噪声RMS的计算式子为
4
k
T
R
(
f
b
−
f
a
)
,
K
=
1.38
×
1
0
−
23
\sqrt{4kTR(f_b-f_a)},K=1.38\times10^{-23}
4kTR(fb−fa),K=1.38×10−23,T为环境温度(开尔文),R为电阻,
f
a
,
f
b
f_a,f_b
fa,fb取值和上面相同。
3. 噪声计算工具
以opa842构成的10倍放大器为例。
首先从手册找出增益带宽积算出截止频率
f
b
f_b
fb
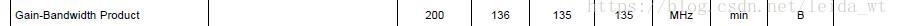
f
b
=
200
10
⋅
1.57
=
31.4
M
H
z
f_b=\frac{200}{10}\cdot 1.57=31.4MHz
fb=10200⋅1.57=31.4MHz
接下来找出噪声参数(宽白噪声)
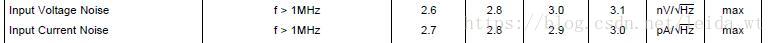
这两个值在手册的噪声频谱图中也有标出。
具体的计算可使用Bruce Trump的一款计算软件,它是个excel表。
下载地址:
链接: https://pan.baidu.com/s/127bnGMkuANfhHZGojgCrZQ?pwd=diw6
提取码: diw6
闪烁噪声(Flicker Noise)与白噪声计算:
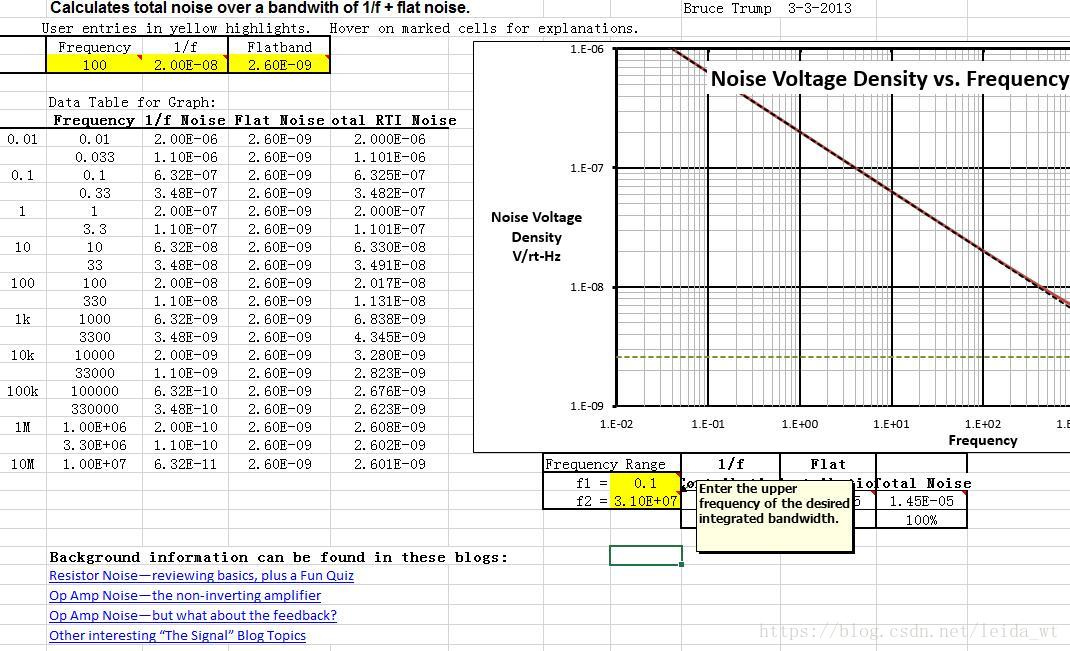
选择Flicker Noise页,在左上角黄色格子依次填入闪烁噪声的值
20
n
V
/
Hz
20nV/\sqrt{\text{Hz}}
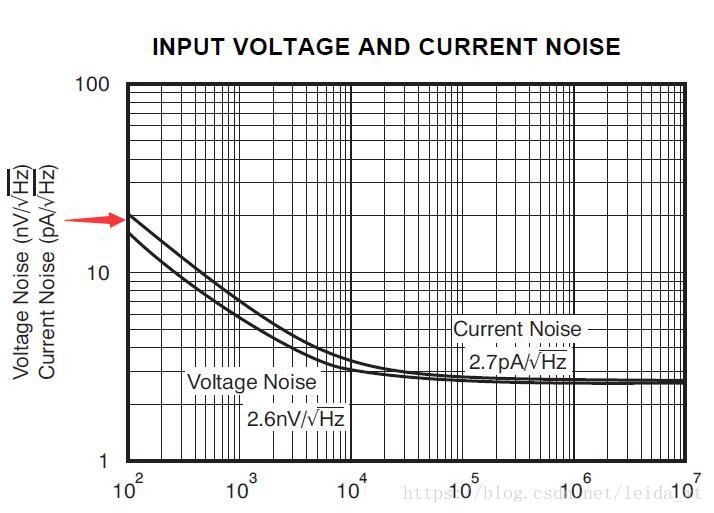
20nV/Hz(100Hz处),以及白噪声的值
2.6
n
V
/
Hz
2.6nV/\sqrt{\text{Hz}}
2.6nV/Hz。都可以从下图读出。
右下角写频率区间:
f
1
=
f
a
=
0.1
Hz
,
f
2
=
f
b
=
31.4
MHz
f_1=f_a=0.1\text{Hz}, f_2=f_b=31.4\text{MHz}
f1=fa=0.1Hz,f2=fb=31.4MHz。计算结果(RMS值)如下图,可见对于这个宽带运放,几乎所有的噪声都来自宽带白噪声(14.5
μ
V
\mu V
μV),1/f噪声(
0.884
μ
V
0.884\mu V
0.884μV)可忽略不计。一般对于带宽大于10KHz的系统,1/f噪声都可忽略。总噪声14.5
μ
V
\mu V
μV再乘噪声增益10就是最后输出噪声。
注: 两个RMS值叠加要取均方和,不是直接相加,故白噪声对总噪声的贡献率接近100%。

运放总噪声计算:
和闪烁噪声计算类似,增加了电阻热噪声的计算。切换到Amplifier Noise页面,根据手册和电路搭建情况分别填写黄色格子中的值。从上到下依次为:信号源电阻、运放电压噪声密度(白噪声)、运放电流噪声密度(白噪声)、反馈电阻、温度(涉及电阻热噪声计算)。这里忽略1/f噪声,故不填写相关数据。
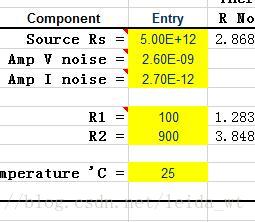
计算结果如下所示为
3.023
×
1
0
−
9
V
/
Hz
3.023\times 10^{-9}V/\sqrt{\text{Hz}}
3.023×10−9V/Hz
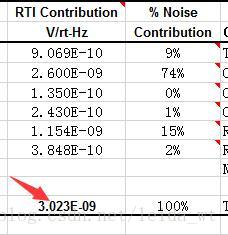
这个数再乘
31.4
MHz
\sqrt{31.4\text{MHz}}
31.4MHz就是运放输出的总电压噪声,约169微伏。可以看到主导噪声源是运放的电压噪声,电阻的热噪声也比较可观。
噪声分析的一些技巧
- 3倍忽略法则。如电压噪声是 3 n V / Hz 3nV/\sqrt{\text{Hz}} 3nV/Hz,电阻热噪声是 1 n V / Hz 1nV/\sqrt{\text{Hz}} 1nV/Hz,则前者对总噪声的贡献是后者的9倍,此时完全可忽略后者的影响。
- 适当选取电阻值,尽量不让电阻热噪声占主导地位。
- FET输入运放一般不需要考虑电流噪声的影响,bipolar输入运放对小于1K的电阻,其电流噪声亦可忽略。
- 对于带宽大于10KHz的系统,白噪声占主导,1/f噪声可忽略。
- 多级放大中,一般第一级增益最大。如第一级增益比后级大3倍以上,则后级放大器的噪声可忽略。
- 引入低通滤波器可显著降低噪声。
参考资料
- TI 高精度实验室系列课程 - 运算放大器噪声 (主要参考)
- 《德州仪器高性能模拟器件选型指南》
- 《新概念模拟电路》
- TI应用笔记-放大器噪声系数计算
- ADI技术文章-关于模拟噪声分析的11个误区
























 7139
7139

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








