【神经网络搜索】ENAS:Efficient Neural Architecture Search

【GiantPandaCV导语】本文介绍的是Efficient Neural Architecture Search方法，主要是为了解决之前NAS中无法完成权重重用的问题，首次提出了参数共享Parameter Sharing的方法来训练网络，要比原先标准的NAS方法降低了1000倍的计算代价。从一个大的计算图中挑选出最优的子图就是ENAS的核心思想，而子图之间都是共享权重的。

1. 摘要

ENAS是一个快速、代价低的自动网络设计方法。在ENAS中，控制器controller通过在大的计算图中搜索挑选一个最优的子图来得到网络结构。

• controller使用Policy Gradient算法进行训练，通过最大化验证集上的期望准确率作为奖励reward。
• 被挑选的子图将使用经典的CrossEntropy Loss进行训练。

子网络之间的权重共享可以让ENAS性能更强大的性能，同时要比经典的NAS方法降低了约1000倍的计算代价。

2. 简介

NAS-RL使用了450个GPU训练了3-4天，花费了32,400-43,200个GPU hours才可以训练出一个合适的网络，需要大量的计算资源。NAS的计算瓶颈就在于需要让每个子模型从头开始收敛，训练完成后就废弃掉其训练好的权重。

本文主要贡献是通过让所有子模型共享权重、避免从头开始训练，从而有效提升了NAS的训练效率。随后的子模型可以通过迁移学习的方法加速收敛速度、从而加速训练。

ENAS可以做到使用单个NVIDIA GTX 1080Ti显卡，只需要花费16个小时。同时在CIFAR10上可以达到2.89%的test error。

3. 方法

3.1 一个例子

ENAS可以看作是从一个超网中得到一个自网络，如下图所示。6个节点相互连接得到的就是超网（是一个有向无环图），通过controller得到红色的路径就是其中的一个子网络。

举一个具体的例子，假设当前有4个节点：

上图是controller，具体实现是一个LSTM，需要做出以下决策：

• 激活哪个边
• 对应Node选择什么操作

第一个Node，controller首先采样一个激活函数，这里采用的是tanh，然后这个激活会接收x和h作为输入。

第二个Node，先采样上一个index=1，说明Node2应该和Node1相连接；然后再采样一个激活函数relu。

第三个Node，先采样上一个index=2，说明Node3应该和Node2相连接；然后采样一个激活函数Relu。

第四个Node，先采样上一个index=1，说明Node4应该和Node1相连接，然后采样一个激活函数tanh。

结束后发现有两个节点是loose end, ENAS的做法是将两者结果做一个平均，得到最终输出。

在上述例子中，假设节点数量为N，一共使用了4个激活函数可选。搜索空间大小为：$4^N\times N!$

其中$4^N$代表N个节点可选的4个激活函数组成的空间，$N!$ 代表节点的连接情况，之所以是阶乘也很容易理解，因为随后的Node只能连接之前出现过的Node。

3.2 ENAS训练流程

在ENAS中，有两组可学习参数，Controller LSTM中的参数$\theta$ 和 子模型共享的权重参数$w$。具体流程是：

• LSTM sample出一个子模型，然后训练模型$w$， 通过标准的反向传播算法进行训练，训练完成以后在验证集上进行测试。
• 通过验证集上结果反馈给LSTM，计算$\theta$的梯度，更新LSTM的参数。
• 如此反复，可以训练出一个LSTM能够让模型在验证集上的性能最佳。

第一步：训练共享参数w

首先固定住controller的参数，然后使用蒙特卡洛估计来计算梯度，更新w权重：

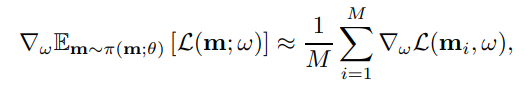
m是从$\pi (m;\theta )$ 中采样得到的模型，对于所有的模型计算模型损失函数的期望。右侧公式是梯度的无偏估计。

第二步：训练controller 参数$\theta$

这一步固定住w，更新controller参数，希望可以得到的Reward值（也就是验证集准确率）尽可能大。

这里使用的是REINFORCE算法来进行计算的，具体内容可以查看NAS-RL那篇文章中的讲解。

3.3 marco search space

有了上边的例子做铺垫，卷积的这部分就很好理解了，区别有几点：

• 节点操作不同，这里可以是3x3卷积、5x5卷积、平均池化、3x3最大池化、3x3深度可分离卷积，5x5深度可分离卷积 一共六个操作。
• 上图Node3输出了两个值，代表先将node1和node2的输出tensor合并，然后在经过maxpool操作。

计算卷积网络设计的空间复杂度，对于第k个节点，顶多可以选取k-1个层，所以在第k层就有$2^{k-1}$种选择，而这里假设一共有L个层需要做从6个候选操作中做选择。那么在不考虑连线的情况下就有 6 L 6^L