本文主要是运用两种方法消除回归模型中的多重共线性问题
一、多重共线性的诊断
扩大因子法
扩大因子法是通过对自变量进行计算的结果：
其中
是自变量的中心化标准矩阵。
是每个自变量的扩大引子。
当
时，则说明
自变量与其他自变量存在严重的多重共线性问题。
代码如下：
from statsmodels.stats.outliers_influence import variance_inflation_factor
import statsmodels.formula.api as smf
import pandas as pd
#读数据
df = pd.read_csv('文件路径')
#建模
result = smf.ols('y~x1+x2+x3+x4',data=df).fit()
#计算扩大引子
VIFlist = [] #保存扩大引子
for i in range(1, 5, 1): #这里循环次数是自变量的个数
vif = variance_inflation_factor(result.model.exog, i) # 参数为设计矩阵和变量数
VIFlist.append(vif)
#以Series格式打印出结果
print('扩大因子法结果：\n',pd.Series(VIFlist))特征根判定法
特征根的方法是计算行列式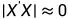
，X 是自变量矩阵。计算该等式的特征根的个数，有多少个特征根接近0，就有几个变量存在多重共线性，然后将最大特征根
和最小特征根
进行计算
当k < 100 时，存在多重共线性
当100 
k1000时，存在较强的多重共线性
当k > 1000时，存在严重的多重共线性。
代码如下：
from statsmodels.stats.outliers_influence import variance_inflation_factor
import statsmodels.formula.api as smf
import pandas as pd
#读数据
df = pd.read_csv('文件路径')
#建模
result = smf.ols('y~x1+x2+x3+x4',data=df).fit()
#计算条件数
print('条件数结果：')
cormatrix = df.iloc[:, 1:].corr(method='pearson') # 相关系数矩阵
eigvalues, eigvec = np.linalg.eig(cormatrix) # eigvalues特征根，eigvec特征向量
Condtion_No = max(eigvalues) / eigvalues
print(pd.Series(Condtion_No)) # 条件数判断二、消除多重共线性
前提准备：
这里先把后面那些方法需要用到的前提函数先准备好，后面就直接讲方法了😘，如下：
import numpy as np
import statsmodels.formula.api as smf
import pandas as pd
from itertools import combinations
# 求所有可能的变量组合
def comb(a): # 参数a为所有自变量的列表
all = []
for i in range(len(a) + 1):
num_choose = i # 从列表a中选num_choose个变量
combins = [c for c in combinations(a, num_choose)]
for i in combins:
i = list(i)
all.append(i)
return all
# 对列表variables中的变量进行组合并建立模型,参数df为读入的数据
def buildModel(variables, df):
combine = ''
for variable in variables:
combine = combine + variable + '+' # 对列表中的变量进行组合
combine = combine[:-1]
if len(combine) == 0:
combine = '1'
result = smf.ols('y~' + combine, data=df).fit() # 得出回归结果
return result
# 变量列表和对应的aic以dataframe的形式输出
def printDataFrame(model, aic): # model为所有备选变量组合的列表，aic为所有备选模型aic的列表
data = {'model': model, 'aic': aic} # 输出Dataframe形式
frame = pd.DataFrame(data)
print(frame)所有子集回归
所有子集回归就是将自变量所有组合列出来，然后对每一个组合进行回归建模，然后通过AIC准则判最小断段选出最优的组合。
# 所有子集回归（主要找AIC最小的自变量组合模型）
def allSubset(a, df): # 参数a为所有自变量的列表，参数df为读入的数据
all = []
all = comb(a) # 先获取所有变量组合组合
aic = [] # 保存所有aic值
for i in all: # 遍历所有组合
result = buildModel(i, df) # 对每一种组合建立模型
aic.append(result.aic) # 获取aic并加入aic列表
printDataFrame(all, aic)
print("最小AIC为：{}".format(min(aic)))
index = aic.index(min(aic))
print("里面包含的自变量为：{}".format(all[index]))
temp = all[index] # 获取最终变量组合
result = buildModel(temp, df) # 输出最终的回归结果
print("回归结果：")
print(result.summary())
#举例
a = ['x1','x2','x3','x4','x5']
df = pd.read_csv('文件路径')
allSubset(a, df)前进法
前进法顾名思义就是一步一步的往前走，就是确定一个初始的变量(一般情况设置为一个常数)，然后再逐步的往模型加变量，然后通过AIC最小选出最佳的自变量个数。
代码如下：
# 前进法
def forward(a, df):
all = []
all = comb(a) # 求所有组合
start = []
for i in range(len(all)): # 把所有长度为0和长度为1的变量组合放入start列表中
if len(all[i]) == 0 or len(all[i]) == 1:
start.append(all[i])
# start=all[:len(a)+1]
while (len(start) > 1):
# variables=[]
aic = []
for i in start: # 遍历所有组合
result = buildModel(i, df) # 对每一种组合建立模型
aic.append(result.aic)
printDataFrame(start, aic) # 输出
print("最小AIC为：{}".format(min(aic)))
index = aic.index(min(aic))
print("里面包含的自变量为：{}".format(start[index]))
temp = start[index]
if (index == 0): # 若aic最小的模型为起始模型则结束循环
break
start = []
start.append(temp) # 下一次循环的起始模型为上一次模型aic最小的模型,起始模型始终是列表的第一个元素
for i in all: # 遍历所有变量组合，选取比起始变量组合多一个变量且拥有起始变量组合所有元素的变量组合
if len(i) == len(temp) + 1 and set(temp) < set(i):
start.append(i)
print("*" * 50)
result = buildModel(temp, df) # 输出最终的回归结果
print("回归结果：")
print(result.summary())
#举例
a = ['x1','x2','x3','x4','x5']
df = pd.read_csv('文件路径')
forward(a, df)后退法
后退法就是将全部变量建立好模型后，将变量一个一个的删除建立模型，通过AIC最小选出最好的组合。
代码如下：
# 后退法
def backward(a, df):
all = []
all = comb(a) # 求所有组合
start = []
for i in range(len(all) - 1, -1, -1): # 把所有长度为len(a)和长度为len(a)-1的变量组合放入start列表中
if len(all[i]) == len(a) or len(all[i]) == len(a) - 1:
start.append(all[i])
while (len(start) > 0):
aic = []
for i in start: # 遍历所有组合
result = buildModel(i, df) # 对每一种组合建立模型
aic.append(result.aic)
printDataFrame(start, aic) # 输出
print("最小AIC为：{}".format(min(aic)))
index = aic.index(min(aic))
print("里面包含的自变量为：{}".format(start[index]))
temp = start[index]
if (index == 0): # 若aic最小的模型为起始模型则结束循环
break
t = set(start[0]).difference(set(temp))
print("删减变量：{}".format(t))
start = [] # 下一次循环的起始模型为上一次模型aic最小的模型
start.append(temp)
for i in all:
if len(i) == len(temp) - 1 and set(temp) > set(i): # 遍历所有变量组合，选取比起始变量组合少一个变量且所有变量都在起始变量组合中的变量组合
start.append(i)
print("*" * 50)
result = buildModel(temp, df) # 输出最终的回归结果
print("回归结果：")
print(result.summary())
#举例
a = ['x1','x2','x3','x4','x5']
df = pd.read_csv('文件路径')
backward(a, df)逐步回归法
该方法是结合了前进法和后退法，先建立全变量的模型，在该模型基础上通过剔除P个变量和添加剩余的m-p个变量，在建立模型，通过AIC最小判断，直到不再添加和剔除则结束，选出aic最小的模型。
# 逐步回归法
def stepWise(a, df):
all = []
dele = [] # 可删减的变量列表
add = [] # 可添加的变量列表
addOrDele = []
var = []
all = comb(a) # 求所有组合
start = []
for i in range(len(all) - 1, -1, -1): # 把所有长度为len(a)和长度为len(a)-1的变量组合放入start列表中
if len(all[i]) == len(a) or len(all[i]) == len(a) - 1:
start.append(all[i])
while (1):
aic = []
for i in start: # 遍历所有组合
result = buildModel(i, df) # 对每一种组合建立模型
aic.append(result.aic)
printDataFrame(start, aic) # 输出
print("最小AIC为：{}".format(min(aic)))
index = aic.index(min(aic))
print("里面包含的自变量为：{}".format(start[index]))
temp = start[index]
if (index == 0): # 若aic最小的模型为起始模型则结束循环
break
if len(temp) > len(start[0]): # 如果最小aic模型的变量组合长度大于起始模型，说明添加了变量
t = set(temp).difference(set(start[0]))
print("增加变量：{}".format(t))
addOrDele.append("+")
var.append(t)
if len(temp) < len(start[0]): # 如果最小aic模型的变量组合长度小于起始模型，说明删减了变量
t = set(start[0]).difference(set(temp))
print("删减变量：{}".format(t))
addOrDele.append("-")
var.append(t)
start = []
start.append(temp)
dele = []
add = []
for i in a:
if i in start[0]:
dele.append(i)
else:
add.append(i)
print("可增加的变量为:{}".format(add))
print("可删减的变量为:{}".format(dele))
# 删除的情况
for i in all: # 选取比起始变量组合多一个变量且拥有起始变量组合所有元素的变量组合
if len(i) == len(temp) - 1 and set(temp) > set(i):
start.append(i)
# 增加的情况
for i in all: # 选取比起始变量组合少一个变量且所有变量都在起始变量组合中的变量组合
if len(i) == len(temp) + 1 and set(temp) < set(i):
start.append(i)
print("*" * 50)
data = {'': addOrDele, 'd': var} # 输出删减增加变量的情况
frame = pd.DataFrame(data)
print(frame)
result = buildModel(temp, df) # 输出最终的回归结果
print("回归结果：")
print(result.summary())
#举例
a = ['x1','x2','x3','x4','x5']
df = pd.read_csv('文件路径')
stepWise(a, df)总结：
以上就是本文的全部内容，有疑问和错误望指出，感谢！一起学习和进步。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
