线性回归之梯度下降法和最小二乘法

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析；如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。常用的方法有梯度下降法和最小二乘法。

1.梯度下降法（GD）

1.1 原理：

        

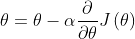
        其中，为学习速率或步长（Learning rate）

1.2 假设函数：

        

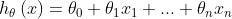
1.3 损失函数：

         

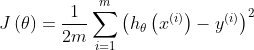
1.4 分析过程：

        1.4.1 批量梯度下降法（BGD）

               批量梯度下降法，是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有m个的样本来进行更新。更新公式为：