传送门
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某一个数加上x
2.求出某区间每一个数的和
输入输出格式
输入格式:第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3个整数,表示一个操作,具体如下:
操作1: 格式:1 x k 含义:将第x个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出包含若干行整数,即为所有操作2的结果。
输入输出样例
输入样例:
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
输出样例:
16
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=10000,M<=10000
对于100%的数据:N<=500000,M<=500000
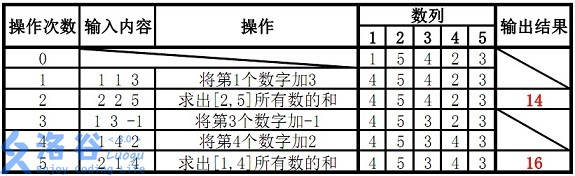
样例说明:
题解
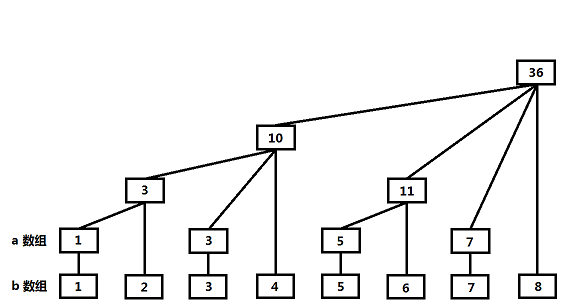
树状数组模板题改点求段啦,至于树状数组,就是下面这个东西:
由于长的像树,于是就取名叫树状数组啦。
树状数组的作用是维护和查询。常见的题目有改点求段,改段求点,改段求段等。
图中的 a 数组就是我们用来维护和查询的数组,b 数组是初值,在实现的代码里是没有用处的。
树状数组的关键操作是lowbit。
lowbit(x)=x & -x; ( -x 就是把 x 按位取反后+1)
lowbit(x)的作用是找到二进制下 x 中最后一个 1 的位置。
如果把树状数组比作老板和员工,那么 x+lowbit(x) 表示的就是比 x 高一级的他的上司,x-lowbit(x) 表示的就是编号在 x 前的第一个不是 x 的下属的人。
于是在我们修改点 x 的值时,只需要从 x 开始不停地往上找 x+lowbit(x),修改便是。
而对于求和,我们定义 sum(x) 返回的是 1~x 的和。就是从 x 开始不停地往下找 x-lowbit(x) ,并且累加。
当我们求 x~y 段的和时,只需要输出 sum(y)-sum(x-1) 即可。
Code:
#include<cstdio>
#include<cstdlib>
int tr[500010];
int n,m;
int lowbit(int x)
{
return x & -x;
}
void add(int x,int k)
{
while(x<=n)
{
tr[x]+=k;
x+=lowbit(x);
}
}
int sum(int x)
{
int ans=0;
while(x!=0)
{
ans+=tr[x];
x-=lowbit(x);
}
return ans;
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
add(i,x);
}
for(int i=1;i<=m;i++)
{
int p,x,y;
scanf("%d %d %d",&p,&x,&y);
if(p==1) add(x,y);
if(p==2) printf("%d\n",sum(y)-sum(x-1));
}
}























 306
306

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








