【动态规划】利润最大化问题

最新推荐文章于 2023-02-02 21:21:17 发布

程序员·小李

最新推荐文章于 2023-02-02 21:21:17 发布

阅读量2.1k

点赞数 1

分类专栏： # 刷刷刷文章标签：动态规划

本文链接：https://blog.csdn.net/Day_and_Night_2017/article/details/123960916

版权

刷刷刷专栏收录该内容

48 篇文章

订阅专栏

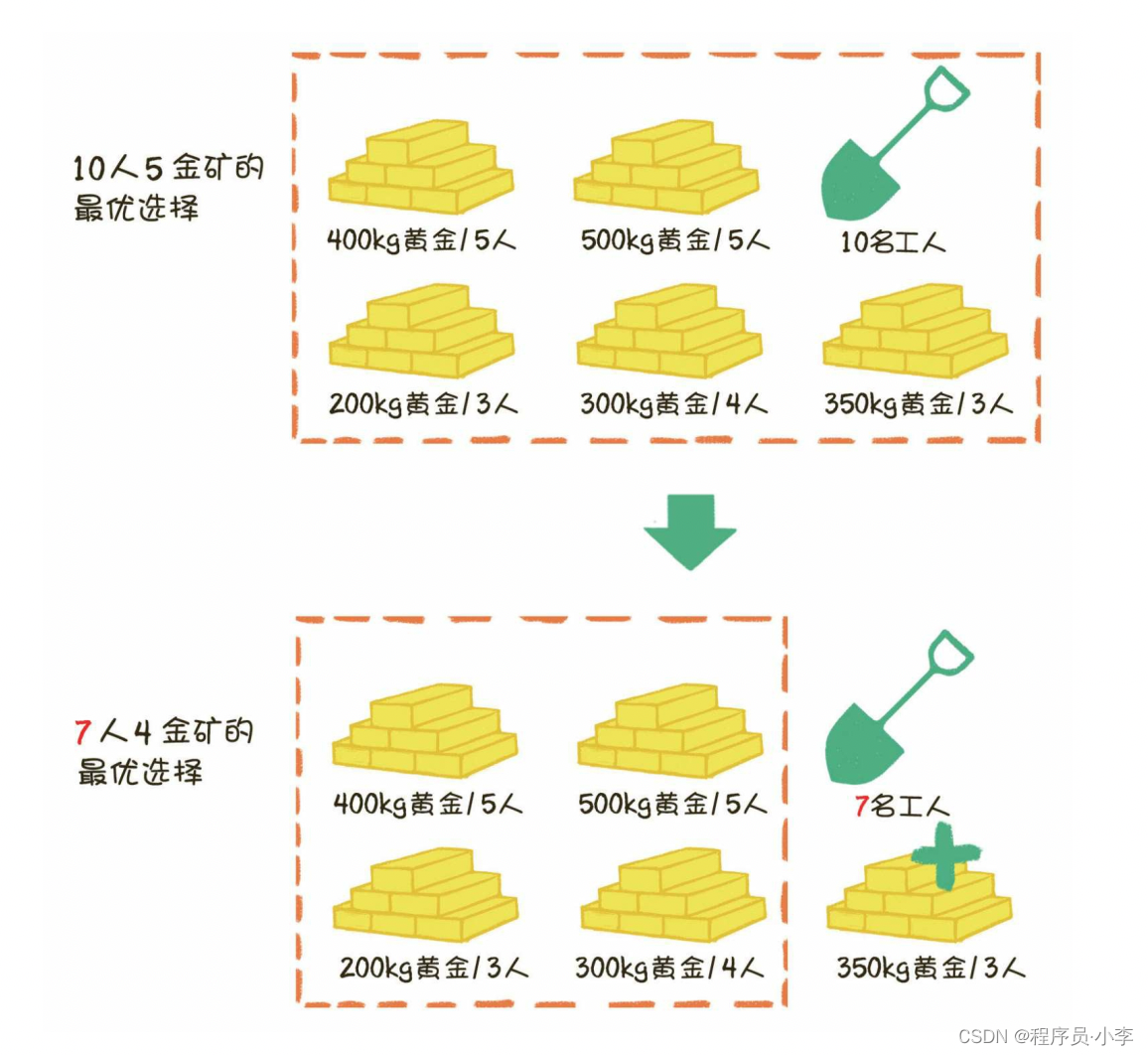
怎么样安排，挖出的黄金最多呢？

这里有两个维度的东西，

一个是收益，分别是200kg, 300kg, 350kg, 400kg, 500kg

一个是成本，分别是3人，4人，3人，5人，5人

可能乍一看，我们会采用贪心算法

首先，计算他们的性价比，200/3，300/4，350/3，400/5，500/5。

然后优先选择性价比较大的。

会导致局部最优解，而非全局最优解。

我们拿出某个黄金来说，只有两个选择，那就是挖或者不挖。

1. 如果不挖，简化为在剩余4个金山中进行选择。

2. 如果挖，简化为除当前黄金以外，从剩下的4个黄金中进行选择，

解法一：递归

// w为人力，n可选项，p为代价，g为收益
public int getBestGoldMining(int w, int n, int[] p, int[] g){
    if(w==0 || n==0){
        return 0;
    }
    
    // 当前人力不足
    if(w < p[n-1]){
        // 跳过当前
        return getBestGoldMining(w, n-1, p, g);
    }
    
    // 不选择当前和选择当前两个方案中选择收益最大的那个
    return Math.max(getBestGoldMining(w, n-1, p, g), getBestGoldMining(w-p[n-1], n-1, p, g)+g[n-1]);
}

解法二：迭代计算

1. 创建数据表，竖向为备选项及其成本/收益，横向为手中的成本能力，空白部分为最大收益。

2. 依次填充空白的部分。

因为400kg的黄金的代价为5个人力，所以第一行空白的1-4个工人的位置，最大收益为0.

此时的w为1，2，3，4，但是p[0] = 5, w < p[0], 推进公式为：

F(n,w) = F(n-1,w) (n>1, w<p[n-1])

则，

F(1,1) = F(1-1,1) = F(0,1) = 0
F(1,2) = F(1-1,2) = F(0,2) = 0
F(1,3) = F(1-1,3) = F(0,3) = 0
F(1,4) = F(1-1,4) = F(0,4) = 0

w为5，6，7，8，9，10时， w >= p[0], 推进公式为：

F(n,w) = max(F(n-1,w), F(n-1,w-p[n-1])+g[n-1]) (n>1, w≥p[n-1]);

则，

F(1, 5) = max(F(0, 5), F(0, 0) + 400) = 400

F(1, 6) = max(F(0, 6), F(0, 1) + 400) = 400

F(1, 7) = max(F(0, 7), F(0, 2) + 400) = 400

F(1, 8) = max(F(0, 8), F(0, 3) + 400) = 400

F(1, 9) = max(F(0, 9), F(0, 4) + 400) = 400

F(1, 10) = max(F(0, 10), F(0, 5) + 400) = 400

对于第二行，

因为500kg的黄金的代价为5个人力，所以第二行空白的1-4个工人的位置，最大收益为0.

此时的w为1，2，3，4，但是p[1] = 5, w < p[0], 推进公式为：

F(n,w) = F(n-1,w) (n>1, w<p[n-1])

则，

F(2,1) = F(2-1,1) = F(1,1) = 0
F(2,2) = F(2-1,2) = F(1,2) = 0
F(2,3) = F(2-1,3) = F(1,3) = 0
F(2,4) = F(2-1,4) = F(1,4) = 0

w为5，6，7，8，9，10时， w >= p[1], 推进公式为：

F(n,w) = max(F(n-1,w), F(n-1,w-p[n-1])+g[n-1]) (n>1, w≥p[n-1]);

则，

F(2, 5) = max(F(1, 5), F(1, 0) + 500) = 500

F(2, 6) = max(F(1, 6), F(1, 1) + 500) = 500

F(2, 7) = max(F(1, 7), F(1, 2) + 500) = 500

F(2, 8) = max(F(1, 8), F(1, 3) + 500) = 500

F(2, 9) = max(F(1, 9), F(1, 4) + 500) = 500

F(2, 10) = max(F(1, 10), F(1, 5) + 500) = 900

对于第三行，

因为200kg的黄金的代价为3个人力，所以第三行空白的1-2个工人的位置，最大收益为0.

此时的w为1，2，但是p[1] = 3, w < p[0], 推进公式为：

F(n,w) = F(n-1,w) (n>1, w<p[n-1])

则，

F(3,1) = F(3-1,1) = F(2,1) = 0
F(3,2) = F(3-1,2) = F(2,2) = 0

当w为3，4，5，6，7，8，9，10时，w >= p[2] 推进公式为：

F(n,w) = max(F(n-1,w), F(n-1,w-p[n-1])+g[n-1]) (n>1, w≥p[n-1]);

则，

F(3, 3) = max(F(2, 3), F(2, 0) + 200) = 200

F(3, 4) = max(F(2, 4), F(2, 1) + 200) = 200

F(3, 5) = max(F(2, 5), F(2, 2) + 200) = 500

F(3, 6) = max(F(2, 6), F(2, 3) + 200) = 500

F(3, 7) = max(F(2, 7), F(2, 4) + 200) = 500

F(3, 8) = max(F(2, 8), F(2, 5) + 200) = 700

F(3, 9) = max(F(2, 9), F(2, 6) + 200) = 700

F(3, 10) = max(F(2, 10), F(2, 7) + 200) = 900

以此类推

第五行

所以最佳答案是900.

public int getBestGoldMiningV2(int w, int[] p, int[] g){
    //创建表格
    int[][] resultTable = new int[g.length+1][w+1];
    //填充表格
    for(int i = 1; i <= g.length; i++){
        for(int j = 1; j <= w; j++){
            if(j<p[i-1]){
                // 当前剩余成本不足以选择当前的方案
                resultTable[i][j] = resultTable[i-1][j];
            }else{
                // 当前成本足够，两个方案的收益取最大值
                resultTable[i][j] = Math.max(resultTable[i-1][j], resultTable[i-1][j-p[i-1]]+ g[i-1]);
            }
        }
    }
    
    //返回最后1个格子的值
    return resultTable[g.length][w];
}

其实我们并不关心j < p[i-1]的部分

public int getBestGoldMiningV3(int w, int[] p, int[] g){
    int[] results = new int[w+1];
    //填充一维数组
    for(int i = 1; i <= g.length; i++){
        for(int j = w; j >= 1; j--){
            if(j >= p[i-1]){
                results[j] = Math.max(results[j], results[j - p[i-1]]+ g[i-1]);
            }
        }
    }

    //返回最后1个格子的值
    return results[w];
}