动态规划
一、定义:
- 动态规划算法通常从问题的子问题出发,基于初始状态最优解以及状态转移方程 找到下一状态的最优解,直至求得我们要解决问题的解。
- 状态:用来描述该问题的子问题的解 dp[n], dp[i][j],
- 状态转移方程:描述状态之间转移的关系式 dp[n] = min/max( dp[n-1], dp[n-2] )
二、举例说明
1.1 爬楼梯
问题描述
一次可以爬 1步或 2步,问一共有多少种爬到 n 阶楼梯的方法?LeetCode 70
动态规划求解
def climbStairs(self, n):
prev, current = 0, 1 # 初始状态
for i in range(n):
prev, current = current, prev + current # 状态转移方程
return current
基本思想:爬上 n 阶的方法数 = n-1 阶的 + n-2 阶的。上面代码从 0 开始计算,爬 1 阶只有一种方法,爬 2 阶的有 1 + 1 种。。。
1.2 Unique Paths (机器人走格子)
问题描述
在 M*N 的格子矩阵中,机器人在 (0,0)处,只能向下或者向右走,一共有多少种方法走到终点(M,N)?LeetCode 62、63
输入举例:m=7, n=3
动态规划求解
def uniquePaths(self, m, n):
dp = [[0 for _ in range(n)] for _ in range(m)]
for index in range(m):
dp[index][0] = 1
for index in range(n):
dp[0][index] = 1
for index_i in range(1, m):
for index_j in range(1, n):
dp[index_i][index_j] = dp[index_i-1][index_j] + dp[index_i][index_j-1]
return dp[m-1][n-1]
基本思路:
- 要解决的问题是: 共有多少种方式到达终点的
- 子问题: 共有多少种方法到达终点的上边和左边。
- 初始状态: 起点的右边和下边只有一种方法到达。
- 状态转移: 到达某一点的方法数 = 到达该店上面的方法数 + 到达该点左面的方法数,即: d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + d p [ i ] [ j − 1 ] dp[i][j] = dp[i-1][j] + dp[i][j-1] dp[i][j]=dp[i−1][j]+dp[i][j−1]
问题拓展
M*N 的格子中存在障碍的点,问此时机器人共有几种方法到达终点?LeetCode 63
解题思路:使用与上面相同的动态规划思想,增加对障碍点的判断,有障碍的点 dp[][] 置零。注意:在第一行和第一列的障碍点会使整行整列障碍后面的点都为零。因为第一行和第一列只能通过前面的一个点到达。
.
三、分析四种典型问题
2.找最少硬币
问题描述
问题: 有价值不同的几种硬币 coinValueList,如何使用数量最少的这些硬币组合出数额 change
eg1: coinValueList = [1, 5, 10, 25], change = 63
eg2: coinValueList = [1, 5, 10, 21, 25], change = 63
可以使用贪心算法,每次取尽可能多面额最大的硬币。但是贪心算法对于不规则的硬币(如:eg2 )就会失效。
递归求最少硬币
def recMakeChange(coinValueList,change):
minCoins = change
if change in coinValueList:
return 1
else:
for i in [c for c in coinValueList if c <= change]:
numCoins = 1 + recMakeChange(coinValueList, change-i)
if numCoins < minCoins:
minCoins = numCoins
return minCoins
- 基本思想:要求解63的最少硬币,就要求得 63-1、63-5、63-10、63-25 的最少硬币+1的数量,… ,终止条件:求 1或5或10或25 的最少硬币数。
- 算法评价:会遍历所有的可能性,能得到最优解。但是存在较多的冗余计算,例如:63-5-5 和 63-10 都会重新计算一次 53 的最少硬币数
- 改进:使用列表保存已经求解过的值,避免重复计算。在上面程序的 if numCoins < minCoins:下面将结果保存到列表 knowResults[change]里面,在程序开头加上判断要计算的 change 是否已经保存在 knowResult 里面。
动态规划求最少硬币
def dpMakeChange(coinValueList,change,minCoins):
for cents in range(change+1):
coinCount = cents
for j in [c for c in coinValueList if c <= cents]:
if minCoins[cents-j] + 1 < coinCount:
coinCount = minCoins[cents-j]+1
minCoins[cents] = coinCount
return minCoins[change]
- 基本思想:从头开始计算所需的最小硬币数,1 所需的硬币,2 所需的硬币数,,,,63 所需的硬币数。例如在求 63 所需的最少硬币数时:只需要找到前面已经计算过的 62、58、53、38 所需硬币数+1后最少的,这就是63的结果。
- 算法评价:与递归的从后往前算不同,这种动态规划的方法是从前往后算,由最简单的状态往后面算。过程更容易理解且不存在递归的冗余计算,复杂度更好分析:len( coinsValueList )*change。
- 改进:上面的代码只计算了最少硬币数。我们可以增加变量,记录使用的硬币分别是什么。其中一种方法是:只记录新使用的硬币,最终使用的硬币可以通过不断向前读取出来。如:coinUsed[ cents ] = newCoin 。那么 63 使用了哪些硬币就保存在 coinUsed [ 63 ]、coinUsed[ 63- coinUsed[63] ]、、、
3. 矩阵相乘加括号
问题描述
矩阵的乘法满足结合律: (A*B)*C*D = A*(B*C)*D,但不同的结合方式会导致矩阵元素之间的乘法次数也是不同的。问:当给定一串连乘的矩阵A*B*C*D*E,如何找到最佳的结合方式,使所需的乘法次数最少?
input:matrixs = [P0, P1, P2, … Pn] 代表n个矩阵连乘,例如:第一个矩阵:A1=P0*P1 其中的P代表行和列的长度。
枚举求解
加括号的方法有 1 n + 1 ( 2 n n ) \frac{1}{n+1}(2n n) n+11(2nn) 是一个Catalan数,指数级别复杂度
动态规划
状态转移方程如下:
m
[
i
]
[
j
]
m[i][j]
m[i][j]代表第 i 个矩阵和第 j 个矩阵连乘时的最少相乘次数。
def matrix_chain(matrixs):
matrix_num = len(matrixs) # 矩阵的个数
m = [[0 for j in range(matrix_num)] for i in range(matrix_num)]
for interval in range(1, matrix_num + 1): # 间隔 1-5 ,因为间隔短的需要被间隔长的使用,如:m[i][i] 每次都会被调用 虽然它一直是0 哈哈哈
for i in range(matrix_num - interval):
j = i + interval
m[i][j] = m[i][i] + m[i + 1][j] + matrixs[i].row_num * matrixs[i + 1].row_num * matrixs[j].col_num
for k in range(i + 1, j):
temp = m[i][k] + m[k + 1][j] + matrixs[i].row_num * matrixs[k + 1].row_num * matrixs[j].col_num
if temp < m[i][j]:
m[i][j] = temp
return m[0][matrix_num - 1]
上面代码中矩阵的定义如下:
class Matrix: # 矩阵的定义
def __init__(self, row_num=0, col_num=0, matrix=None):
if matrix != None:
self.row_num = len(matrix)
self.col_num = len(matrix[0])
esle:
self.row_num = row_num
self.col_num = col_num
self.matrix = matrix
.
4.多起点多终点最短路径问题
问题描述
求解图中由 S 到 T 的最短路径:
该问题的求解思想与下面的LeetCode 120 的思路一样。请看下面LeetCode 120 的题目解析:
.
LeetCode 120.Triangle
状态函数:
d
p
[
i
]
[
j
]
dp[i][j]
dp[i][j] 表示(i,j)位置的点到最低端的最小路径值。
代码实现:
#LeetCode 120 Triangle三角列表 状态转移方程
#dp[i][j] = min{dp[i+1][j], dp[i+1][j+1]} + triangle[i][j]
class Solution(object):
def minimumTotal(self, triangle):
if not triangle or triangle == [[]]:
return 0
for items in range(len(triangle)-2, -1, -1): #从倒数第二层开始
for i in range(len(triangle[items])):
triangle[items][i] = min(triangle[items+1][i],triangle[items+1][i+1]) + triangle[items][i] #递推式
return triangle[0][0]
基本思路:从末端开始,把每个点到终点的最短距离都保存下来。然后在计算上一层的时候就会用到前面保存的最短距离,直至回退到起点处。结果就是起点到终点的最短距离。
.
类似例题:
LeetCode 300.Longest Increasing Subsequence
#LeetCode 300 Longest Increasing Subsequence最长递增子序列
class Solution(object):
def lengthOFLIS(self, nums):
if nums == []:
return 0
ans = 0
dp = [1 for _ in range(len(nums))]
for i in range(1,len(nums)):
for j in range(i):
if nums[i] > nms[j]:
dp[i] = max(dp[j]+1, dp[i]) #递推式
ans = max(ans, dp[i])
return ans
LeetCode 53.Maximum Subarry
#LeetCode 53 Maximum Subarray 和最大的连续子序列
class Solution(object):
def maxSubArray(self, nums):
maxmum = min(nums)
maxSub = [maxmum]
for i in range(1,len(nums)):
m = max(maxSub[i-1] + nums[i], nums[i]) #递推式
maxSub.append(m)
return max(maxSub)
.
5.最长公共子序列
问题描述
状态函数的定义:
C
[
i
]
[
j
]
C[i][j]
C[i][j]表示序列
x
1
,
x
2
,
x
3
,
.
.
.
,
x
i
x_1,x_2, x_3,...,x_i
x1,x2,x3,...,xi 和 序列
y
1
,
y
2
,
y
3
,
.
.
.
,
y
j
y_1, y_2,y_3,...,y_j
y1,y2,y3,...,yj 的最长公共子序列。
s1 = ['A','B','C','B','D','A','B']
s2 = ['B','D','C','A','B','A']
d = [[0]*(len(s2)+1) for i in range(len(s1)+1) ]
for i in range(1, len(s1)+1):
for j in range(1, len(s2)+1):
if s1[i-1] == s2[j-1]:
d[i][j] = d[i-1][j-1]+1
else:
d[i][j] = max(d[i-1][j], d[i][j-1])
print("Number of LCS:", d[-1][-1])
.
四、总结
从上面的 爬楼梯、走格子、换硬币、矩阵连乘、最长公共子序列 这些类型题来看,好像动态规划就是从前往后计算,把前面的每个状态都保存下来提供给下一状态的计算(即状态转移)。但是看了最短路径那题,动态规划又不能简单的归结为从前往后计算。思考一下之后发现,这些题目的动态规划都有的特点是:它们都是递归的逆向求解。上面的题目都是可以写成递归的形式的,但是递归会涉及到很多的重复计算,递归的层数不能太多,不然函数栈就容易溢出。而动态规划正是从另一个方向来解决问题,保存子问题的状态,从而更简单有效地计算后面状态的问题。典型例子可参看上面的换硬币问题。








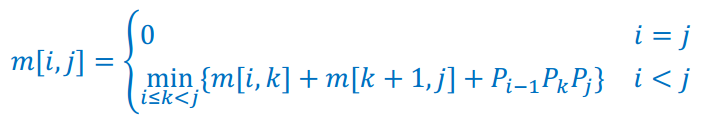

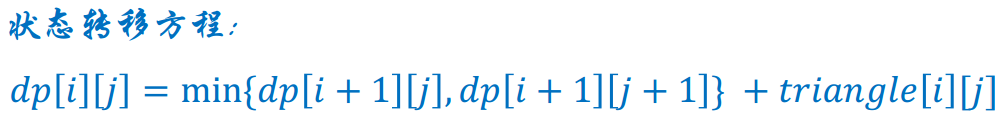
















 1757
1757











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








