Colored Cubes
There are several colored cubes. All of them are of the same size but they may be colored differently. Each face of these cubes has a single color. Colors of distinct faces of a cube may or may not be the same.
Two cubes are said to be identically colored if some suitable rotations of one of the cubes give identical looks to both of the cubes. For example, two cubes shown in Figure 2 are identically colored. A set of cubes is said to be identically colored if every pair of them are identically colored.
A cube and its mirror image are not necessarily identically colored. For example, two cubes shown in Figure 3 are not identically colored.
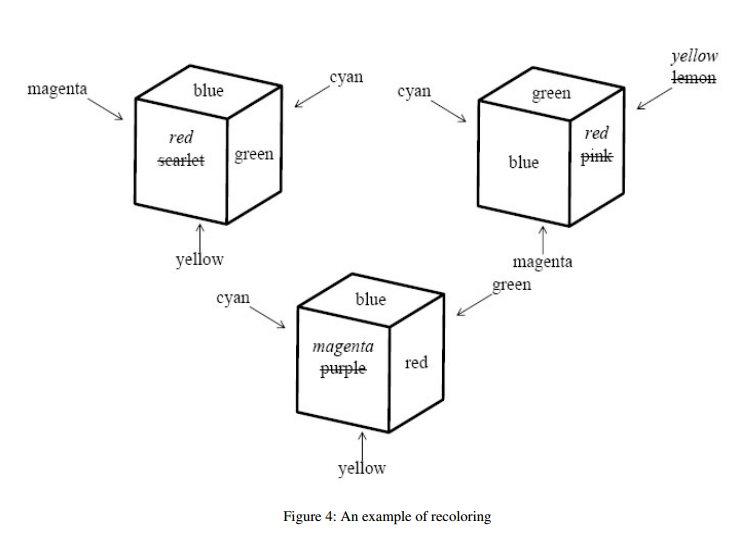
You can make a given set of cubes identically colored by repainting some of the faces, whatever colors the faces may have. In Figure 4, repainting four faces makes the three cubes identically colored and repainting fewer faces will never do.
Your task is to write a program to calculate the minimum number of faces that needs to be repainted for a given set of cubes to become identically colored.
Input
The input is a sequence of datasets. A dataset consists of a header and a body appearing in this order. A header is a line containing one positive integer n and the body following it consists of n lines. You can assume that 1 <= n <= 4 . Each line in a body contains six color names separated by a space. A color name consists of a word or words connected with a hyphen (-). A word consists of one or more lowercase letters. You can assume that a color name is at most 24-characters long including hyphens.
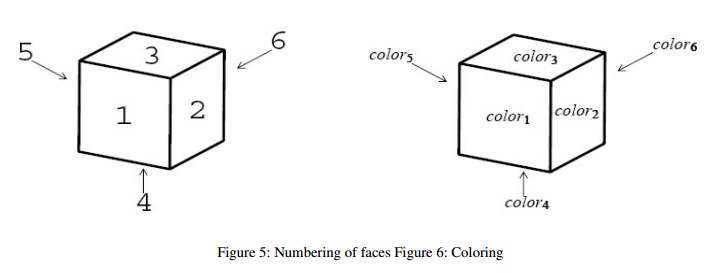
A dataset corresponds to a set of colored cubes. The integer n corresponds to the number of cubes. Each line of the body corresponds to a cube and describes the colors of its faces. Color names in a line is ordered in accordance with the numbering of faces shown in Figure 5. A line:
color1color2color3color4color5color6
corresponds to a cube colored as shown in Figure 6.
The end of the input is indicated by a line containing a single zero. It is not a dataset nor a part of a dataset.
Output
For each dataset, output a line containing the minimum number of faces that need to be repainted to make the
set of cub es identically colored.
Sample Input
3
scarlet green blue yellow magenta cyan
blue pink green magenta cyan lemon
purple red blue yellow cyan green
2
red green blue yellow magenta cyan
cyan green blue yellow magenta red
2
red green gray gray magenta cyan
cyan green gray gray magenta red
2
red green blue yellow magenta cyan
magenta red blue yellow cyan green
3
red green blue yellow magenta cyan
cyan green blue yellow magenta red
magenta red blue yellow cyan green
3
blue green green green green blue
green blue blue green green green
green green green green green sea-green
3
red yellow red yellow red yellow
red red yellow yellow red yellow
red red red red red red
4
violet violet salmon salmon salmon salmon
violet salmon salmon salmon salmon violet
violet violet salmon salmon violet violet
violet violet violet violet salmon salmon
1
red green blue yellow magenta cyan
4
magenta pink red scarlet vermilion wine-red
aquamarine blue cyan indigo sky-blue turquoise-blue
blond cream chrome-yellow lemon olive yellow
chrome-green emerald-green green olive vilidian sky-blue
0
Sample Output
4
2
0
0
2
3
4
4
0
16
这几个题目的难度真的是上了一个档次,通过做这几道题无论是思维量还是代码量都得到了一定程度的提升,此题的重点是在于打表和爆搜判断。
首先,打表程序,他是为了实现穷举同一个立方体的不同摆放方式,需要明确这样两个数组,P[i]=j表示编号 i 在 j 位置,T[x]=y表示在x位置上的编号经过“变换T”到了y位置上。
如果理解这一点了之后,那么这个打表程序就很好实现了,他的思想和Piotr's Ants那一道题一样,都利用到了映射、反映射的思想。
其次,爆搜判断,考验代码能力和思维能力的地方,头脑要清晰:
1.dfs到n个立方体的一种摆放状态时进行判断;
2.判断时首先要根据dfs出的第i个立方体的一种状态r[i],求出第i个立方体对应的r[i]状态的摆放方式,即color[i][dice24[r[i]][j]]=dice[i][j];
3.记录好本次状态每个立方体的摆放方式后,对n个立方体逐个面的去比较,每个面求出n个立方体中拥有共同颜色最多的数量maxface,则n-maxface即为当前面的修改次数(count数组记录每个颜色在n个立方体的公共面的出现次数);
4.求出六个面的修改总次数后,若此状态下情况更优则更新答案;
5.爆搜穷举出所有状态后,即为最佳修改次数。
注意:宏定义时MAXN千万不要忘加括号
本题透露出来了我在字符串使用方面概念模糊的缺点,我打算再开一篇文章专门总结一下字符串的用法。不久会贴出链接。
附代码如下:
24种状态的生成程序:
#include<cstdio>
#include<cstring>
using namespace std;
int left[6]={4,0,2,3,5,1};
int up[6]={2,1,5,0,4,3};
int rot(int* T,int* p){
int q[6];
memcpy(q,p,sizeof(q));
for(int i=0;i<6;i++)p[i]=T[q[i]];
return 0;
}
int main(){
freopen("Colored Cubes.cpp","w",stdout);
int st[6]={0,1,2,3,4,5};
printf("int dice24[24][6]={\n");
for(int i=0;i<6;i++){
int ed[6];
memcpy(ed,st,sizeof(st));
if(i==0){rot(up,ed);}
if(i==1){rot(left,ed);rot(up,ed);}
if(i==3){rot(up,ed);rot(up,ed);}
if(i==4){rot(left,ed);rot(left,ed);rot(left,ed);rot(up,ed);}
if(i==5){rot(up,ed);rot(up,ed);rot(up,ed);}
for(int j=0;j<4;j++){
printf("{%d,%d,%d,%d,%d,%d,},\n",ed[0],ed[1],ed[2],ed[3],ed[4],ed[5]);
rot(left,ed);
}
}
printf("};\n");
fclose(stdout);
return 0;
}
程序(爆搜+判断)代码:
int dice24[24][6]={
{2,1,5,0,4,3,},
{2,0,1,4,5,3,},
{2,4,0,5,1,3,},
{2,5,4,1,0,3,},
{4,2,5,0,3,1,},
{5,2,1,4,3,0,},
{1,2,0,5,3,4,},
{0,2,4,1,3,5,},
{0,1,2,3,4,5,},
{4,0,2,3,5,1,},
{5,4,2,3,1,0,},
{1,5,2,3,0,4,},
{5,1,3,2,4,0,},
{1,0,3,2,5,4,},
{0,4,3,2,1,5,},
{4,5,3,2,0,1,},
{1,3,5,0,2,4,},
{0,3,1,4,2,5,},
{4,3,0,5,2,1,},
{5,3,4,1,2,0,},
{3,1,0,5,4,2,},
{3,0,4,1,5,2,},
{3,4,5,0,1,2,},
{3,5,1,4,0,2,}
};
#include<cstdio>
#include<vector>
#include<cstring>
#include<string>
using namespace std;
#define MAXN (4+2)
vector<string> cNames;
int dice[MAXN][6],r[MAXN],color[MAXN][6];
int n,ans;
int ID(const char* cName){
string s(cName);
int len=cNames.size();
for(int i=0;i<len;i++){
if(s==cNames[i])return i;
}
cNames.push_back(s);
return len;
}
void check(){
for(int i=0;i<n;i++){
for(int j=0;j<6;j++){
color[i][dice24[r[i]][j]]=dice[i][j];
}
}
int total=0;
for(int i=0;i<6;i++){
int count[MAXN*6];
memset(count,0,sizeof(count));
int maxface=0;
for(int j=0;j<n;j++){
maxface=max(maxface,++count[color[j][i]]);
}
total+=n-maxface;
}
ans=min(ans,total);
}
void dfs(int x){
if(x==n)
check();
else
for(int i=0;i<24;i++){
r[x]=i;
dfs(x+1);
}
}
int main(){
//freopen("in.txt","r",stdin);
while(scanf("%d",&n)==1&&n){
cNames.clear();
for(int i=0;i<n;i++){
for(int j=0;j<6;j++){
char cName[30];
scanf("%s",cName);
dice[i][j]=ID(cName);
}
}
ans=6*n;
r[0]=0;
dfs(1);
printf("%d\n",ans);
}
//fclose(stdin);
return 0;
}























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








