洛谷P2680 运输计划

P2680 [NOIP 2015 提高组] 运输计划 - 洛谷

求最长路径的最小值，想到二分答案。

那么该如何验证答案的正确性呢？

我们可以令一条边的边权变为0，我们自然是希望把所有路径都经过次数最多的边变为0。

那么该如何统计每条边被所有路径使用的次数呢？

答案是树上差分了

比如 在这颗树上，对路径（3，4）（2，5）进行边差分，然后求前缀和  

              

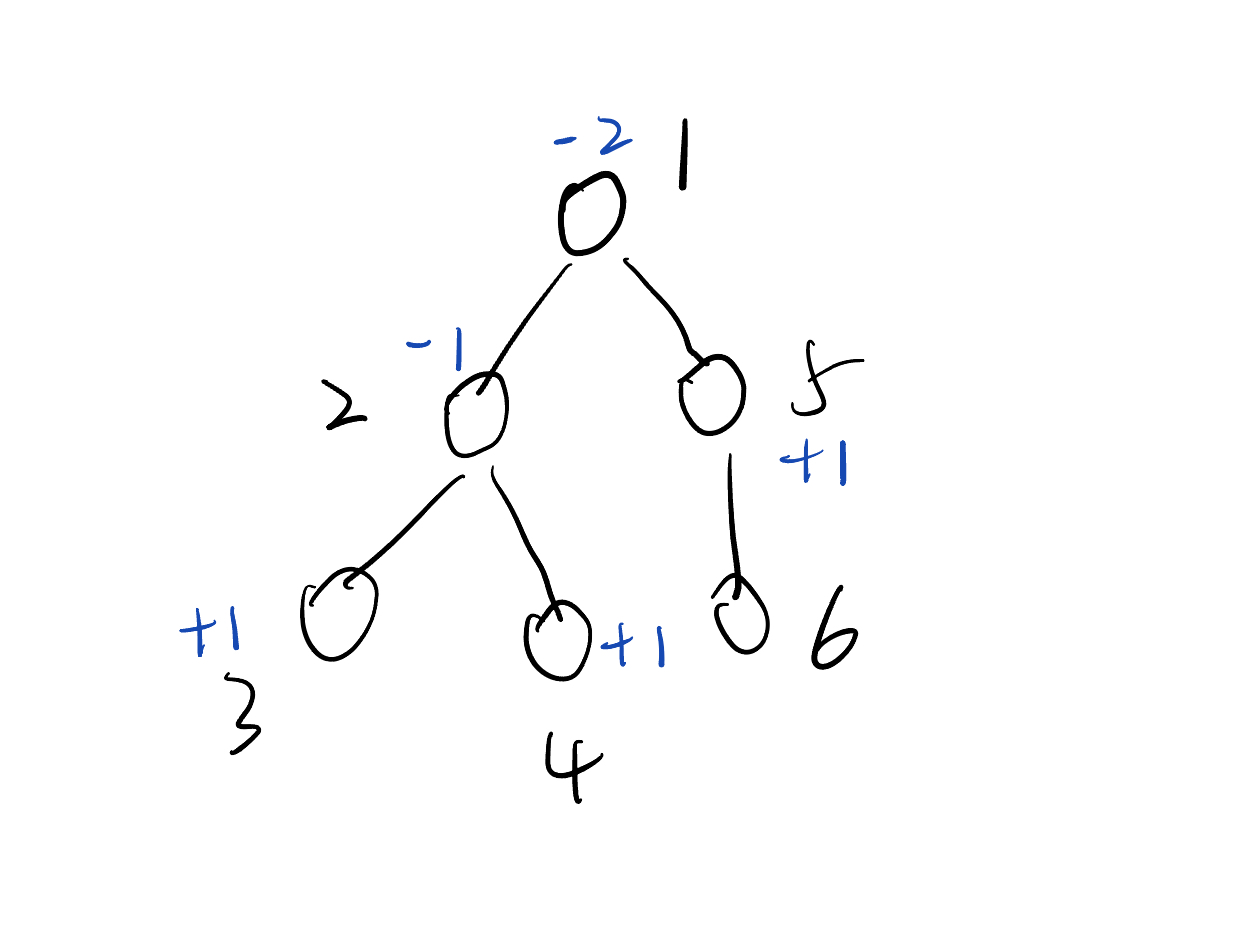
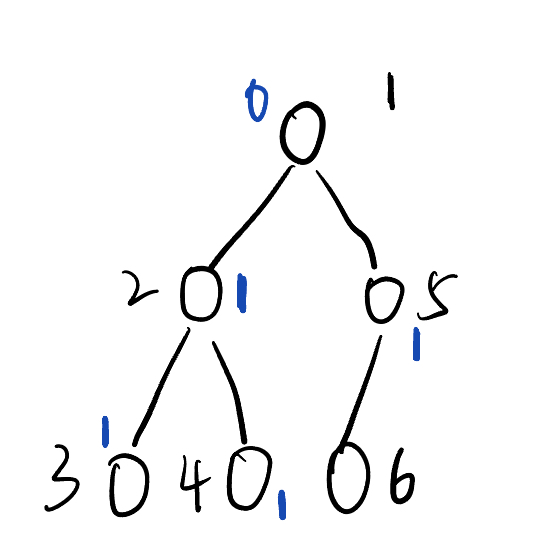
右图是我们的前缀和，节点旁边的数字代表即代表这条边的使用次数。接下来就可以愉快的二分了。

我们规定路径长度 L，tree[u],表示u到其父亲的边被使用的次数，edge[u]表示u到其父亲的边的权值

对于每一个答案K我们只需要关心路径长度 L，其中 L  > K 的路径就可以了。

我们记所有路径中L > K  的个数为 cnt，将这些路径使用边差分，然后前缀和得到的就是被这些路径使用的边的次数因为这些路径都不满足条件，我们要让他们都的L < K，就要选择(tree[u] >= cnt && edge[u] >= maxd)的边变为0，若存在这样的一条边，显然这个答案是合法的，否则不合法

贴上代码

#include <bits/stdc++.h>

using namespace std;

const int MAXN = 300010;

int n, m, tree[MAXN], dep[MAXN], fa[MAXN][25], path[MAXN], arc[MAXN];

struct lane
{
    int u, v, lca, cost;
};

struct node
{
    int v, w;
};

vector <lane> road;
vector <node> edge[MAXN];
/----------------lca--------------*/
void dfs(int u, int father)
{
    dep[u] = dep[father] + 1;
    fa[u][0] = father;
    for(int i = 1; i <= 20; i++)
    {
        fa[u][i] = fa[fa[u][i-1]][i-1];
    }
    for(auto it: edge[u])
    {
        if(it.v == father) continue;
        arc[it.v] = it.w;
        path[it.v] = it.w + path[u];
        dfs(it.v, u);
    }
}

int lca(int u, int v)
{
    if(dep[u] < dep[v]) swap(u, v);
    if(dep[v] == 1) return v;
    for(int i = 20; ~i; i--)
    {
        if(dep[fa[u][i]] >= dep[v]) u = fa[u][i];
    }
    if(u == v) return u;
    for(int i = 20; ~i; i--)
    {
        if(fa[u][i] == fa[v][i]) continue;
        u = fa[u][i];
        v = fa[v][i];
    }
    return fa[u][0];
}

int dis(int u, int v)
{
    return path[u] + path[v] - 2 * path[lca(u,v)];
}
/*---------------二分-----------------*/
void dfs1(int u, int father)
{
    for(auto it: edge[u])
    {
        if(it.v == father) continue;
        dfs1(it.v, u);
        tree[u] += tree[it.v];
    }
}

bool check(int v)
{
    int cnt = 0, maxd = 0;
    for(int i = 0; i <= n; i++)tree[i] = 0;
    for(auto it: road)
    {
        if(it.cost > v)
        {
            maxd = max(maxd, it.cost - v);
            cnt++;
            tree[it.u]++;
            tree[it.v]++;
            tree[it.lca] -= 2;
        }
    }
    dfs1(1, 0);
    for(int i = 1; i <= n;i ++)
    {
        if(tree[i] >= cnt && arc[i] >= maxd) return 1;
    }
    return 0;
}


int solve()
{
    int l = 0, r = 1e9;
    if(check(l)) return l;
    while(l + 1 != r)
    {
        int mid = (l + r) / 2;
        if(check(mid)) r = mid;
        else l = mid;
    }
    return r; 
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i < n; i++)
    {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        edge[u].push_back({v, w});
        edge[v].push_back({u, w});
    }
    dfs(1, 0);
    for(int i = 0; i < m; i++)
    {
        int u, v;
        scanf("%d%d", &u, &v);
//        printf("%d %d\n", lca(u, v), dis(u, v));
        road.push_back({u, v, lca(u, v), dis(u, v)});
    }
    printf("%d", solve());
    return 0;
}