基于MATLAB梯形法求积分

这是一个定积分的问题。

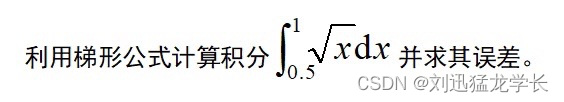
题目

我们可以打开MATLAB并搭建脚本文件（开心心）

x=0:0.01:1;
y=sqrt(x);
plot(x,y,'-k');

确保编程无误后，点击运行，好开心！图像出来啦！

注意哈，时间间隔不能太短也不能太长，间隔大的话，曲线不平滑，间隔小的话，定点很麻烦，因为鼠标的一个微小位移都会导致定点不准，举个例子，如果自变量间隔是0.001的话，我想定点为0.1的话，很有可能便宜到0.999或者1.001，这是最糟心的事儿了，我就经历过，希望大家吸取教训哈。

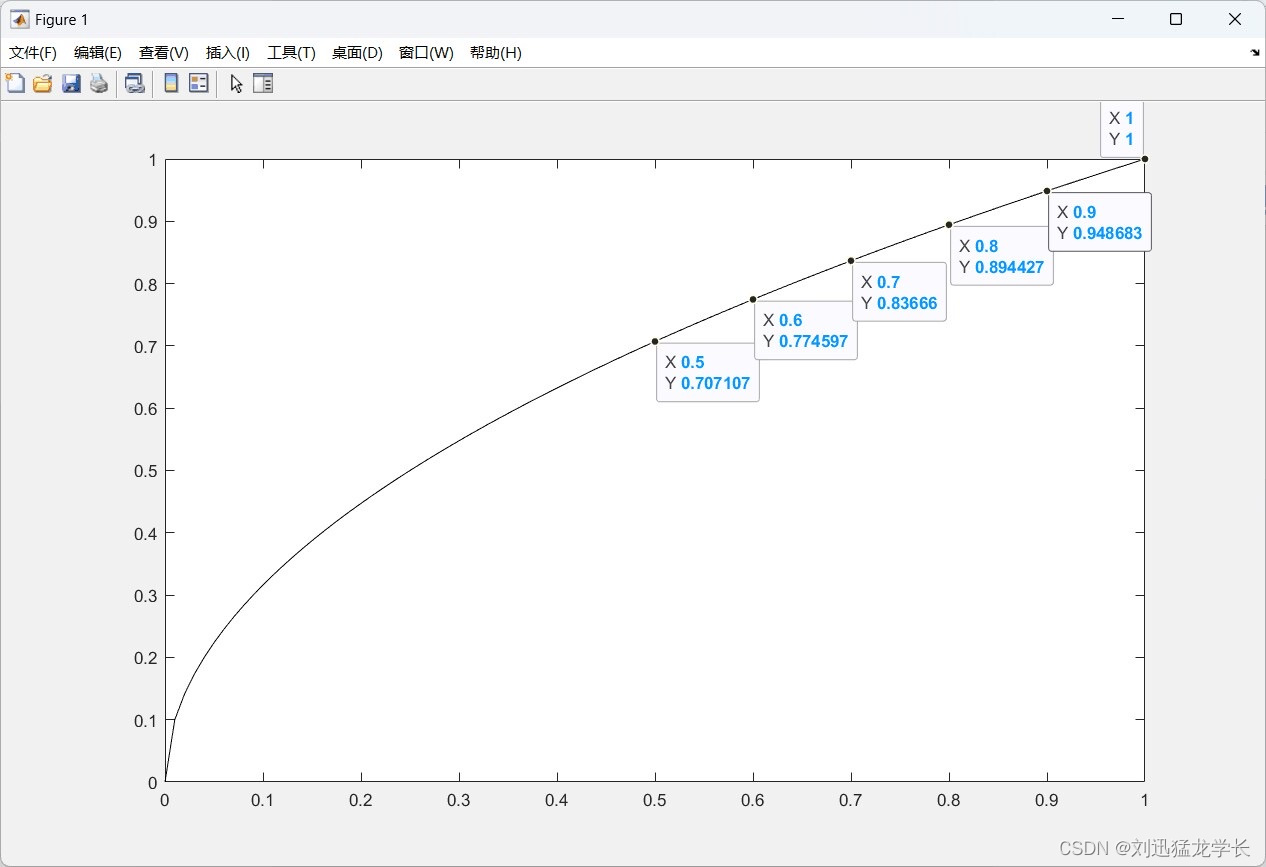
运行结果

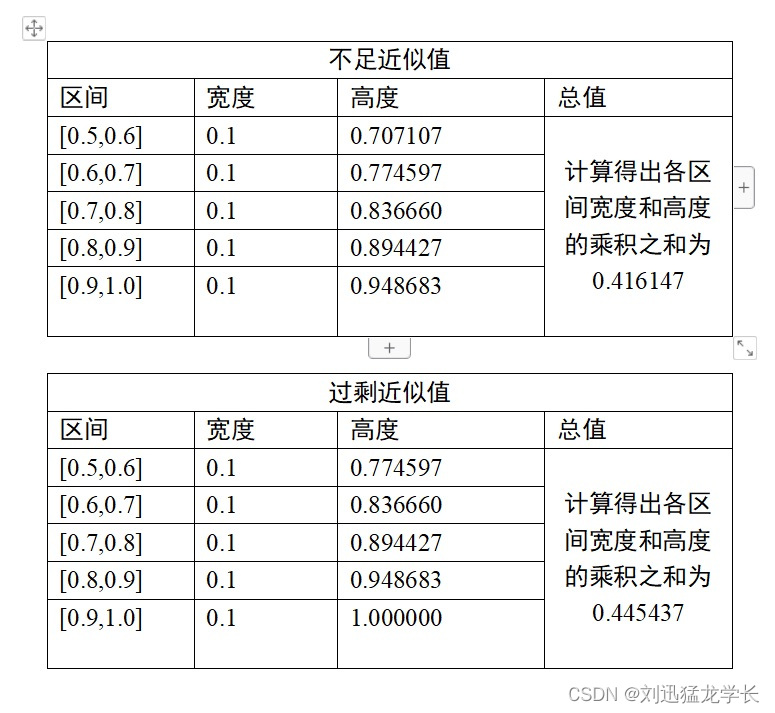
不足近似值和过剩近似值的计算结果

---

我们用物理实验精确度计算方法“四舍六入五凑偶”去算。

四舍六入五凑偶，说到底也不难理解，举个例子：比如说你要精确到千分位，四舍就是万分位如果不高于4就舍去，2.5612记作2.561；六入就是万分位不低于6，千分位加一，4.3388记作4.339；五凑偶就是万分位是5的时候，千分位是偶数就把0.0005舍去，千分位是奇数就加到相邻的一个偶数上去，比如圆周率π=3.1415926，可记作3.142，1.5565则记为1.556。

计算得出该定积分的不足近似值为0.416417，过剩近似值为0.445437。