【动态规划】C++ dp子数组问题（最大/最长：环形/子数组和、乘积最大/为正数、单词拆分、子串）

1. 前言 - 理解动态规划算法

关于 动态规划的理解 与例题，点击👇

【动态规划】C++解决斐波那契模型题目（三步问题、爬楼梯、解码方法…）

有了上面的经验，我们来解下面 子数组问题 ：

2. 例题

下面的例题帮助我们理解子数组类问题的解法：

最大子数组和

• 题意分析
  1. 题目要求找一个连续子数组 其总和最大。
  2. 要求很直白，我们根据要求设置状态表示即可：

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n + 1); // 创建dp数组
        // dp[0] = 0; 默认为0
        
        int ret = INT_MIN;
        for(int i = 1; i <= n; ++i)
        {
            dp[i] = max(nums[i - 1], dp[i-1] + nums[i - 1]);
            ret = max(ret, dp[i]);
        }
        
        return ret;
    }
};

---

3. 算法题

3.1_环形子数组的最大和

思路

• 题意分析
  1. 题目要求获得 环形子数组的最大和
  2. 主要问题在于如何对环形这一特点进行操作，我们可以分为两种情况：

有了上面两种状态，自然我们可以创建两个dp数组，下面进行状态表示设置：

随后进行 内容初始化以及其他细节：

代码

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& nums) {
        int n = nums.size();
        // 创建dp数组
        vector<int> f(n + 1); // 记录到i位置时的子数组最大和
        auto g = f; // 记录到i位置时的子数组最小和

        // dp数组的计算
        int fmax = INT_MIN, gmin = INT_MAX, sum = 0;
        for(int i = 1; i <= n; ++i)
        {
            int x = nums[i - 1];

            f[i] = max(x, f[i-1] + x);
            fmax = max(fmax, f[i]); // f最大和
            
            g[i] = min(x, g[i-1] + x);
            gmin = min(gmin, g[i-1]); // g最小和

            sum += x; // 统计数组总和
        }

        // 当nums全部为负数时，sum - g[i]为0，而子数组最少要选择一位
        return sum == gmin ? fmax : max(fmax, sum - gmin);
    }
};

---

3.2_乘积最大子数组

思路

• 题意分析
  1. 本题要求找到 连续子数组的最大乘积，乘积与和的差别在于，乘积需要考虑负数的影响，所以这里需要两个dp表：

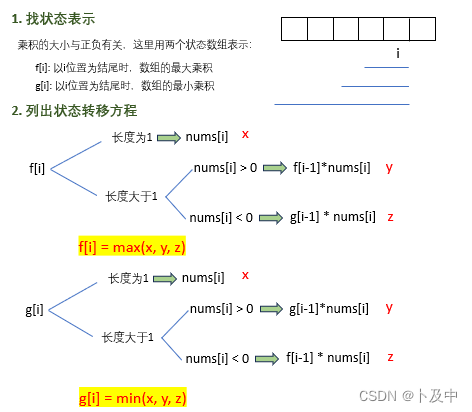
代码

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n+1); // 以i位置为结尾时，数组的最大乘积
        auto g = f; // 以i位置为结尾时，数组的最小乘积

        f[0] = g[0] = 1; // 初始化
        int ret = INT_MIN;
        for(int i = 1; i <= n; ++i)
        {
            int x = nums[i-1], y = f[i-1] * nums[i - 1], z = g[i-1] * nums[i - 1];
            f[i] = max(max(x, y), z);
            g[i] = min(min(x, y), z);
            ret = max(ret, f[i]);
        }

        return ret;
    }
};

---

---

3.3_乘积为正数的最长子数组长度

思路

• 题意分析
  1. 题目要求找 乘积为正数 的 最长子数组的长度 ，注意这里要的是长度
  2. 乘积有正负之分，我们依然创建两个dp表：

代码

class Solution {
public:
    int getMaxLen(vector<int>& nums) {
        int n = nums.size();
        vector<int>f(n + 1), g(n + 1); // 创建dp数组
        // 默认初始化为f[0] = g[0] = 0;

        int ret = 0;
        for(int i = 1; i <= n; ++i)
        {
            if(nums[i - 1] > 0) {
                f[i] = f[i-1] + 1;
                g[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;
            } else if(nums[i - 1] < 0) {
                f[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;
                g[i] = f[i-1] + 1;
            }
            ret = max(ret, f[i]);
        }

        return ret;
    }
};

---

3.4_等差数列划分

思路

• 题意分析
  1. 题目要求找到的 所有为等差数列的子数组，并返回总个数
  2. 根据要求我们可以直接设置dp状态表示：

代码

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n); // dp[i]: 以i为结尾的子数组中等差数列的个数
        // dp[0] = dp[1] = 0; // 默认为0，无需初始化

        int sum = 0; // 记录等差数列的个数
        for(int i = 2; i < n; ++i)
        {
            dp[i] = nums[i] - nums[i-1] == nums[i-1] - nums[i-2] ? dp[i-1] + 1 : 0;
            sum += dp[i];
        }

        return sum;
    }
};

---

3.5_最长湍流子数组

思路

• 题意分析
  1. 题目要求找到所有的属于 的 湍流数组 的子数组的的 个数 ，什么是湍流数组？
  2. 如图所示，湍流数组可以理解为，递增递减关系是以上一下/一下一上的
     
  3. 如何解决？可以看出来湍流数组实际上是有两种形态的，即对于最后一个状态，其为上升态或是下降态，我们可以以此创建两个dp表：

代码

class Solution {
public:
    int maxTurbulenceSize(vector<int>& arr) {
        int n = arr.size();
        // 创建dp数组 + 初始化
        // 以i为结尾的所有子数组中，为上升 / 下降状态的最长长度
        vector<int> f(n, 1), g(n, 1);
        
        int ret = 1;
        for(int i = 1; i < n; ++i)
        {
            if(arr[i - 1] < arr[i]) f[i] = g[i-1] + 1;
            else if(arr[i-1] > arr[i]) g[i] = f[i-1] + 1;
            ret = max(ret, max(f[i], g[i]));
        }

        return ret;
    }
};

---

3.6_单词拆分

思路

• 题意分析
  1. 根据题目要求我们可以设置状态表示：

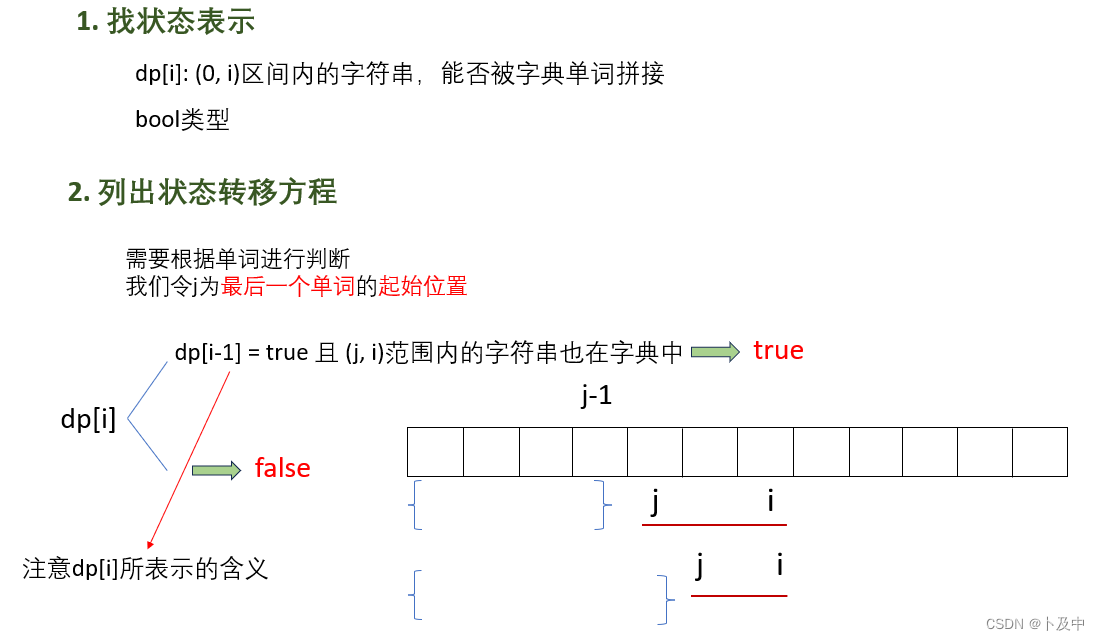
代码

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        // 优化：利用哈希表存储数组中的单词
        unordered_set<string> hash;
        for(auto& word : wordDict)
            hash.insert(word);

        int n = s.size();
        vector<bool> dp(n + 1, false); // dp[i] 表示前 i 个字符能否被拆分
        dp[0] = true; // 空字符串可以被拆分

        for (int i = 1; i <= n; ++i)
            for (int j = i - 1; j >= 0; --j) 
            {
                if (dp[j] && hash.count(s.substr(j, i - j))) 
                {
                    dp[i] = true;
                    break;
                }
            }

        return dp[n];
    }
};

---

467.环绕字符串中唯一的子字符串

思路

• 题意分析

  1. 根据题目：base为一个无限环绕的26个字母的字符串，需要找到给定字符串中 的 属于base 的非空子串的个数
  2. 如上根据题目要求，我们可以设置状态表示：

  

代码

class Solution {
public:
    int findSubstringInWraproundString(string s) {
        int n = s.size();
        // 创建dp数组 + 初始化
        vector<int> dp(n, 1); // dp[i]: 以i为结尾的所有子数组中，在base里的数组个数
        // 填数组
        for(int i = 1; i < n; ++i)
            if(s[i-1]+1 == s[i] || (s[i-1] == 'z' && s[i] == 'a'))
                dp[i] += dp[i-1]; // 相当于dp[i] = dp[i-1]+1
    
        // 哈希表用于找：以该字符为结尾的，最长的数组中，在base 的数组个数
        int hash[26] = {0};
        for(int i = 0; i < n; ++i)
            hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);

        // 返回值
        int ret = 0;
        for(int num : hash)
            ret += num;

        return ret;
    }
};